Similar presentations:
Свойства логарифмов. Уроки №75-76
1.
ДР№1.Теория. Прочитать текст §2, Глава VII,
Знать определение логарифма и
свойства.
Разобрать все задачи в параграфе
2.Практика.
№№777-783(2)
2. Приветствую вас на уроке
Уроки №75-76Приветствую вас
на уроке
Девиз урока:
Некоторые наиболее часто
встречающиеся виды
трансцендентных функций, прежде
всего показательные, открывают
доступ ко многим исследованиям.
3. Свойства логарифмов
Уроки №75-7624.01.2021
Свойства логарифмов
Успешного усвоения учебного материала
4.
Прочитайте свойства логарифмовa 0, a 1, b 0, c 0, k 0
1) log a (bc) log a b log a c
2) log a (b : c) log a b log a c
3) log a b r log a b
1
4) log a k b log a b
k
r
5.
№7771) log 10 5 log 10 2
log 10 (5 2) log 10 10 1
2) log 10 8 log 10 125
log 10 (8 125) log 10 1000 3
6.
№7773) log 12 2 log 12 72
log 12 (2 72) log 12 144 2
3
4) log 3 6 log 3
2
3
log 3 (6 ) log 3 9 2
2
7.
№77815
1) log 2 15 log 2
16
15
log 2 (15 : ) log 2 16 4
16
2) log 5 75 log 5 3
log 5 (75 : 3) log 5 25 2
8.
№7783) log 1 54 log 1 2
3
3
log 1 (54 : 2) log 1 27 3
3
3
9.
№7781
4) log 8 log 8 32
16
1
1
log 8 ( : 32) log 8
3
16
512
10.
№7792
5
1) log 13 169 log 13 13
5
2
2
log 13 13
5
5
2) log 11
3
2
3
2
121 log 11 11
3
11.
№7795
4
3) log 1 243 log 1 3
4
3
3
5
4
1
5
log 1 ( )
3
4
3
7
1
7
6
4) log 2 6
log 2 2
6
128
12.
№7801) log 8 12 log 8 15 log 8 20
12
4
4
log 8 ( 20) log 8 16 log 23 2
15
3
2) log 9 15 log 9 18 log 9 10
3
log 9 (15 18 : 10) log 9 27
2
13.
№7801
3
3) log 7 36 log 7 14 3 log 7 21
2
1
2
log 7 36 log 7 14 log 7 ( 21)
3
log 7 6 log 7 14 log 7 21
6
1
log 7
log 7
2
14 21
49
3
14.
№7801
3
4)2 log 1 6 log 1 400 3 log 1 45
2
3
3
3
1
2
log 1 6 log 1 400 log 1 ( 45 )
2
3
3
3
3
3
3
log 1 36 log 1 20 log 1 45
3
36 45
log 1
log 1 81 4
20
3
3
3
15.
a 0, b 0№781
1) log 3 (27 а b )
2
log 3 27 log 3 а b
2
1
2
3 log 3 (а b )
1
2
3 log 3 а log 3 b
1
3 log 3 а log 3 b
2
16.
a 0, b 0№781 3
а
2
3
2) log 3 2 log 3 а log 3 (9b )
9b
1
3
log 3 а (log 3 9 log 3 b )
1
2
log 3 а 2 log 3 b
3
1
2 log 3 а 2 log 3 b
3
2
17.
№7813) log 3
a 0, b 0
81 а
3
2
3
2
b 3
3
2
log 3 (81 а ) log 3 b
3
2
2
3
log 3 81 log 3 а log 3 b
3
2
4 log 3 а log 3 b
2
3
18.
№7814) log 3
4
аb
3
5
a 0, b 0
2
ab
log 3 аb log 3 a b
2
4
1
4
3
2
4
5
5
3
1
3
log 3 (а b ) log 3 (a b )
19.
№781a 0, b 0
1
4
1
2
5
3
1
3
log 3 а log 3 b log 3 а log 3 b
5
1
1
1
log 3 а log 3 b log 3 а log 3 b
4
2
3
3
17
1
log 3 а log 3 b
12
6
20.
№7821)log a x log а (а b
3 2
c)
21.
№7821)log a x log а (а b
3 2
c)
1
2
log а а log а b log a c
3
2
22.
№7821)log a x log а (а b
3 2
c)
1
2
log а а log а b log a c
1
3 log а а 2 log а b log a c
2
3
2
23.
№7821)log a x log а (а b
3 2
c)
1
2
log а а log а b log a c
1
3 log а а 2 log а b log a c
2
1
3 2 3 ( 2) 8
2
3
2
24.
№7822)log a x log а
а
43
3
1
3
b
c
4
3
log а а log а b log a c
1
4 log а а log а b 3 log a c
3
1
4 3 3 ( 2) 11
3
25.
№7833
log 3 8 log 3 2 3 log 3 2 3
1)
4
log 3 16 log 3 2 4 log 3 2 4
3
log 5 27 log 5 3 3 log 5 3 3
2)
2
log 5 9 log 5 3 2 log 5 3 2
26.
№783log 5 36 log 5 12
3)
log 5 9
36
log 5
log 5 3 1
12
2
log 5 3
2 log 5 3 2
27.
№783log 7 8
4)
log 7 15 log 7 30
3
log 7 8
log 7 2
3
3
1
15 log 7 2
1
log 7
30
28.
Проверка усвоения материалаВычислить:
1) log 9 45 log 9 1,8
2) log 11 121
5
29.
Проверка усвоения материала30.
Проверка усвоения материалаВычислить:
1
3)2 log 0,3 3 log 0,3 10000
2
31.
Проверка усвоения материала32.
Проверка усвоения материалаЗная, что :
log 5 а 4, log 5 b 7
1) log 5 (аb )
3
2) log 5
a
b
2
33.
Проверка усвоения материала34.
Проверка усвоения материала35.
Проверка усвоения материала36.
.2020Классная работа
Свойства логарифмов
Глава VII.§2
37. Цели урока:
- Ознакомиться со свойствамилогарифмов
- Продолжить формирование
культуры устной и письменной
математической речи, умения
оценивать уровень своих знаний
по рассматриваемой теме.
38.
Прочитайте свойства логарифмовa 0, a 1, b 0, c 0, k 0
1) log a (bc) log a b log a c
2) log a (b : c) log a b log a c
3) log a b r log a b
1
4) log a k b log a b
k
r
39.
№784(1)1
log 2 24 log 2 72
2
1)
1
log 3 18 log 3 72
3
40.
№784(1)1
log 2 24 log 2 72
2
1)
1
log 3 18 log 3 72
3
log 2 24 log 2 72
log 3 18 log 3 72
1
2
1
3
41.
№784(1)24
log 2
log 2 24 log 2 72
72
1
18
3
log 3 3
log 3 18 log 3 72
72
1
2
42.
24log 2
log 2 24 log 2 72
72
1
18
3
log 3 3
log 3 18 log 3 72
72
24
log 2
6
2
18
log 3 3
2 9
№784(1)
1
2
43.
№784(1)4
24
log 2
log 2
2
6
2
9
18
log 3 3
log 3 3
9
2 9
44.
№784(1)2
2
4
24
log 2 1
log 2
log 2
2
2
6
2
2
2
9
18
3
log 3 3
log 3 3
log 3 2
9
2 9
3
3
45.
№784(1)2
2
4
24
log 2 1
log 2
log 2
2
2
6
2
2
2
9
18
3
log 3 3
log 3 3
log 3 2
9
2 9
3
3
3
2
log 2 2
4
3
log 3 3
46.
№784(1)3
log 2 2
log 2 2
2
4
4
3
log 3 3
log 3 3
3
3
2
47.
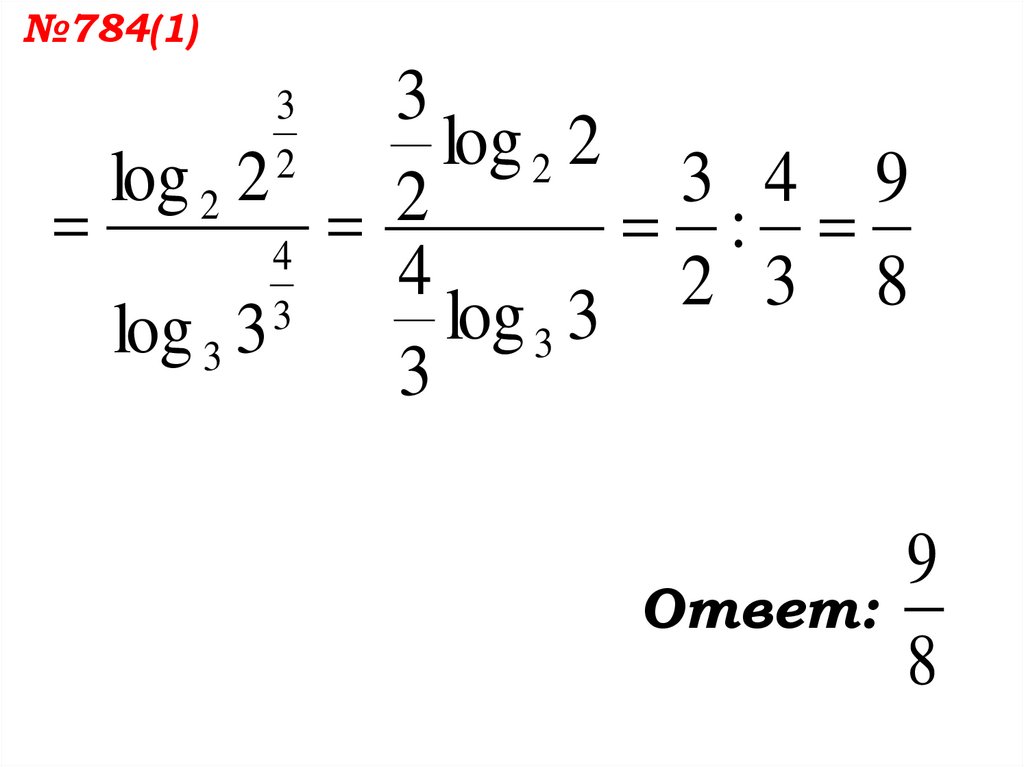
№784(1)3
log 2 2
log 2 2
3 4 9
2
:
4
4
2
3
8
3
log 3 3
log 3 3
3
3
2
Ответ:
9
8
48.
Выполните устно:Найти х по данному его
логарифму:
1) log 3 x log 3 4
2) log 7 x log 7 4 log 7 5
3) log 5 x 2 log 5 6
49.
№785(1)Найти х по данному его
логарифму ( а 0; b 0)
1) log 3 x 4 log 3 а 7 log 3 b
50.
№785(1)Найти х по данному его
логарифму ( а 0; b 0)
1) log 3 x 4 log 3 а 7 log 3 b
log 3 x log 3 а log 3 b
4
7
51.
№785(1)Найти х по данному его
логарифму ( а 0; b 0)
1) log 3 x 4 log 3 а 7 log 3 b
log 3 x log 3 а log 3 b
4
log 3 x log 3 (а b )
4 7
7
52.
№785(1)Найти х по данному его
логарифму ( а 0; b 0)
1) log 3 x 4 log 3 а 7 log 3 b
log 3 x log 3 а log 3 b
4
log 3 x log 3 (а b )
4 7
x а b
4 7
7
53.
№785(3)Найти х по данному его
логарифму ( а 0; b 0)
2
1
3) log 1 x log 1 а log 1 b
3 2
5 2
2
54.
№785(3)Найти х по данному его
логарифму ( а 0; b 0)
2
1
3) log 1 x log 1 а log 1 b
3
5
2
2
2
2
3
log 1 x log 1 а log 1 b
2
2
2
1
5
55.
№785(3)(а 0; b 0)
Найти х по данному его логарифму
2
1
3) log 1 x log 1 а log 1 b
3
5
2
2
2
2
3
log 1 x log 1 а log 1 b
2
2
2
а
log 1 x log 1 5
b
2
2
3
2
1
5
56.
№785(3)(а 0; b 0)
Найти х по данному его логарифму
2
1
3) log 1 x log 1 а log 1 b
3 2
5 2
2
2
3
log 1 x log 1 а log 1 b
2
2
1
5
2
а
log 1 x log 1 5 ;
b
2
2
3
2
а
x 5
b
3
2
57.
№786(3)Вычислить:
1 log4 5
16
4
1
log2 3 3 log8 5
2
58.
№786(3)Вычислить:
1 log4 5
16
16 16
1
4
log4 5
1
log2 3 3 log8 5
2
4
1
log2 3
2
4
3 log8 5
59.
№786(3)Вычислить:
16 16
1
16 4
1
log4 5
2 log4 5
4
2
1
log2 3
2
1
2 log2 3
2
4
2
3 log8 5
2 3log 3 5
2
60.
№786(3)Вычислить:
16 4
1
2 log4 5
16 4
2
log4 5 2
1
2 log2 3
2
2
log2 3
2
2
2 3log 3 5
2
3
2
log2 5
3
61.
№786(3)Вычислить:
16 4
1
2 log4 5
16 4
2
log4 5 2
1
2 log2 3
2
2
log2 3
2
2
16 25 3 25 475
2 3log 3 5
2
3
2
log2 5
3
62.
Прочитайте свойства логарифмовa 0, a 1, b 0, c 0, k 0
1) log a (bc) log a b log a c
2) log a (b : c) log a b log a c
3) log a b r log a b
1
4) log a k b log a b
k
k
5) log аk x log a x
r
63.
№787(3)Выразить данный логарифм
через логарифм по основанию 2:
log 2 13
64.
№787(3)Выразить данный логарифм
через логарифм по основанию 2:
log 2 13 log 1 13
22
65.
№787(3)Выразить данный логарифм
через логарифм по основанию 2:
1
log 2 13 log 1 13 log 2 13
1
2
2
2
66.
№787(3)Выразить данный логарифм
через логарифм по основанию 2:
1
log 2 13 log 1 13 log 2 13
1
22
2
2 log 2 13
67.
№787(1)Выразить данный логарифм
через логарифм по основанию 2:
log 4 5
68.
№787(1)Выразить данный логарифм
через логарифм по основанию 2:
log 4 5 log 2 2 5
69.
№787(1)Выразить данный логарифм
через логарифм по основанию 2:
1
log 4 5 log 2 2 5 log 2 5
2
70.
№788(3)Вычислить:
log 1 7
36
log 36 49
71.
№788(3)Вычислить:
log 1 7
36
log 36 49
log 36 1 7
log 36 7
2
72.
№788(3)Вычислить:
log 1 7
log
log
7
1 7
36
36
36
2
log 36 49 log 36 7
2 log 36 7
73.
№788(3)Вычислить:
log 1 7
log
log
7
1 7
1
36
36
36
2
2 log 36 7
2
log 36 49 log 36 7
74.
№789(1)Вычислить:
1
log 36 2 log 1 3
2 6
75.
№789(1)Вычислить:
1
log 36 2 log 1 3
2 6
1
2
log 62 2 log 6 1 3
76.
№789(1)Вычислить:
1
log 36 2 log 1 3
2 6
1
2
log 62 2 log 6 1 3
1
2
1
log 6 2 ( 1) log 6 3
2
77.
№789(1)1
Вычислить: log 36 2 log 1 3
2 6
1
2
log 62 2 log 6 1 3
1
1
2
log 6 2 ( 1) log 6 3
2
1
2
1
2
log 6 2 log 6 3
78.
1Вычислить: log 36 2 log 1 3
2 6
1
2
log 62 2 log 6 1 3
1
1
2
log 6 2 ( 1) log 6 3
2 1
1
1
1
№789(1)
log 6 2 log 6 3 log 6 (2 3 )
2
2
2
2
79.
№789(1)Вычислить:
1
log 36 2 log 1 3
1
2 6
log 62 2 log 6 1 3 2
1
2
1
log 6 2 ( 1) log 6 3
2
1
1
1
1
2
2
2
2
log 6 2 log 6 3 log 6 (2 3 )
1
2
log 6 6
80.
№789(1)Вычислить:
1
log 36 2 log 1 3
1
2 6
log 62 2 log 6 1 3 2
1
2
1
log 6 2 ( 1) log 6 3
2
1
1
1
1
2
2
2
2
log 6 2 log 6 3 log 6 (2 3 )
1
2
1
log 6 6
2
81.
№791(1)r
log а k x log a x
k
r
Выразить:
log 9 а
4
82.
№791(1,3)Выразить:
r
log а k x log a x
k
r
log 9 а log 32 а
4
4
83.
№791(1,3)r
log а k x log a x
k
r
Выразить:
4
log 9 а log 32 а log 3 а
2
4
4
84.
№791(1,3)r
log а k x log a x
k
r
Выразить:
4
log 9 а log 32 а log 3 а
2
2 log 3 а
4
4
85.
№791(1,3)r
log а k x log a x
k
r
Выразить:
log
а
3
86.
№791(1,3)r
log а k x log a x
k
r
Выразить:
log
log
а
1 а
3
32
87.
№791(1,3)r
log а k x log a x
k
r
Выразить:
1
log 3 а log 1 а log 3 а
1
2
3
2
88.
№791(1,3)r
log а k x log a x
k
r
Выразить:
1
log 3 а log 1 а log 3 а
1
2
3
2
2 log 3 а
89.
№795(1,3)Выразить через а и b:
log 3 15 a,
log 3 50
log 3 10 b
90.
№795(1,3)Выразить через а и b:
log 3 15 a,
log 3 10 b
log 3 50 2 log 3 50
91.
№795(1,3)Выразить через а и b:
log 3 15 a,
log 3 10 b
log 3 50 2 log 3 50
2 log 3 (10 5)
92.
№795(1,3)Выразить через а и b:
log 3 15 a,
log 3 10 b
log 3 50 2 log 3 50
2 log 3 (10 5)
2 log 3 10 2 log 3 5
93.
№795(1,3)Выразить через а и b:
log 3 15 a,
log 3 15
log 3 10 b
94.
№795(1,3)Выразить через а и b:
log 3 15 a,
log 3 10 b
log 3 15 log 3 (3 5)
95.
№795(1,3)Выразить через а и b:
log 3 15 a, log 3 10 b
log 3 15 log 3 (3 5) log 3 3 log 3 5
96.
№795(1,3)Выразить через а и b:
log 3 15 a, log 3 10 b
log 3 15 log 3 (3 5) log 3 3 log 3 5
log 3 15 1 log 3 5
97.
№795(1,3)Выразить через а и b:
log 3 15 a, log 3 10 b
log 3 15 log 3 (3 5) log 3 3 log 3 5
log 3 15 1 log 3 5
log 3 5 a 1
98.
№795(1,3)Выразить через а и b:
log 3 15 a, log 3 10 b
log 3 5 a 1,
log 3 50 2 log 3 10 2 log 3 5
99.
№795(1,3)Выразить через а и b:
log 3 15 a, log 3 10 b
log 3 5 a 1,
log 3 50 2 log 3 10 2 log 3 5
2b 2a 2
100.
Оценки за урок:Оцените ваше усвоение материала в
классе:
«5»- все было понятно и задания
выполнялись без особого труда;
«4» – были трудные моменты, осталось
еще раз разобрать задания, чтобы не было
проблем в будущем;
«3»- остались непонятными некоторые
задания из-за пробелов в знаниях. Следует
поработать индивидуально.



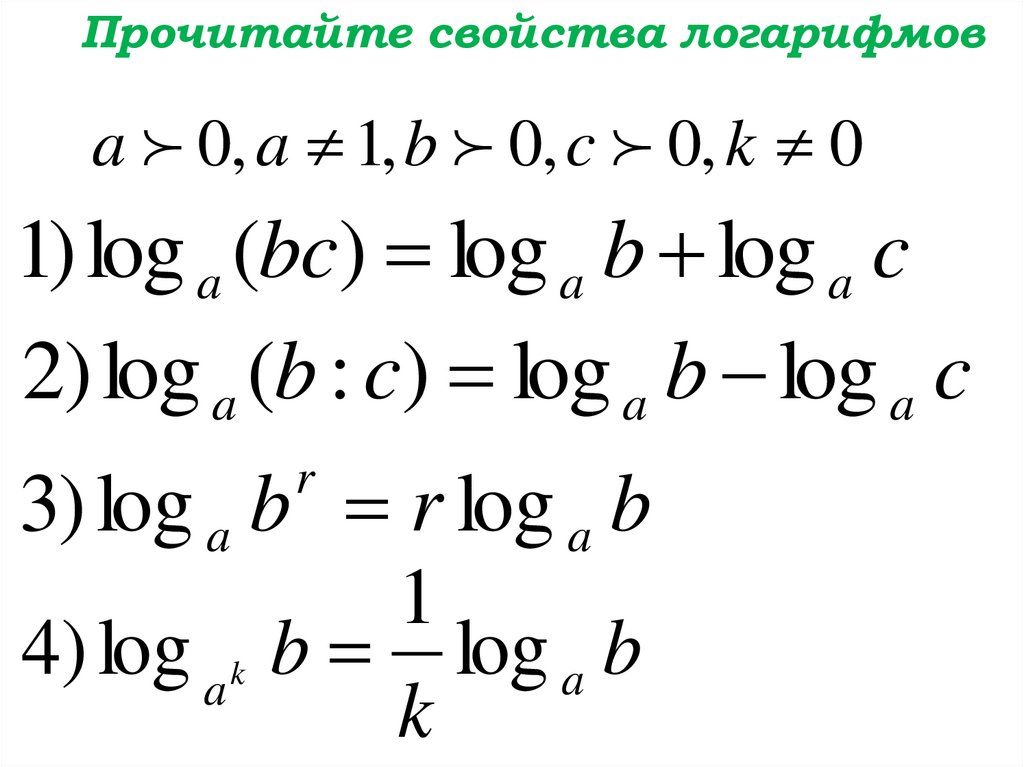

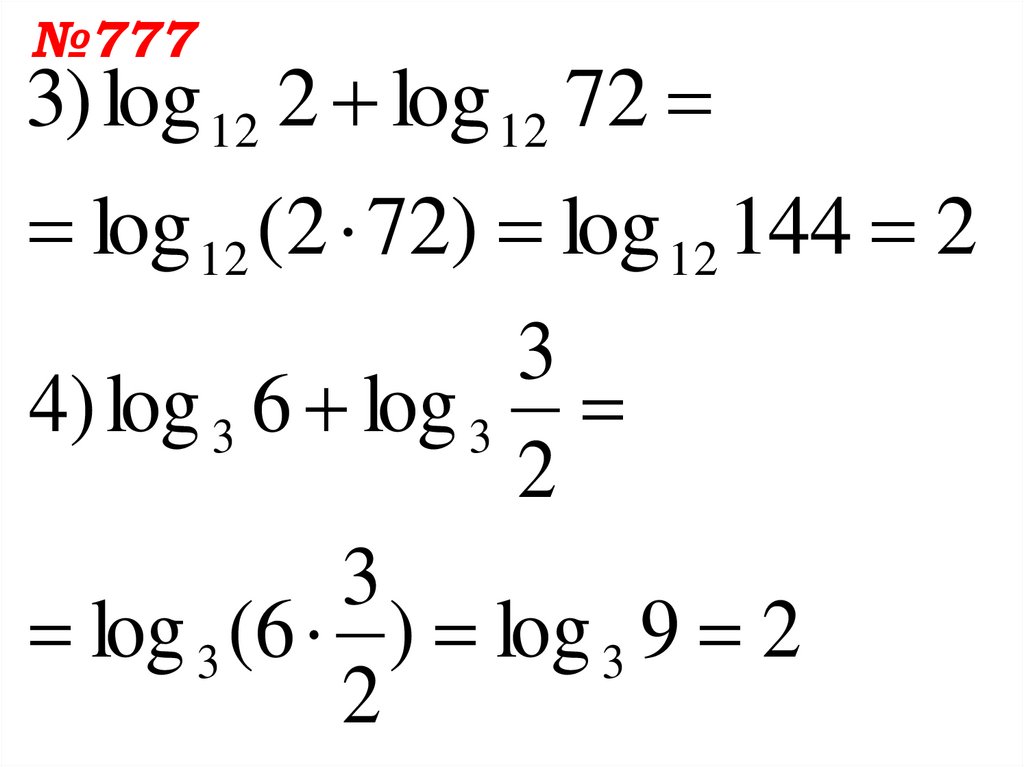

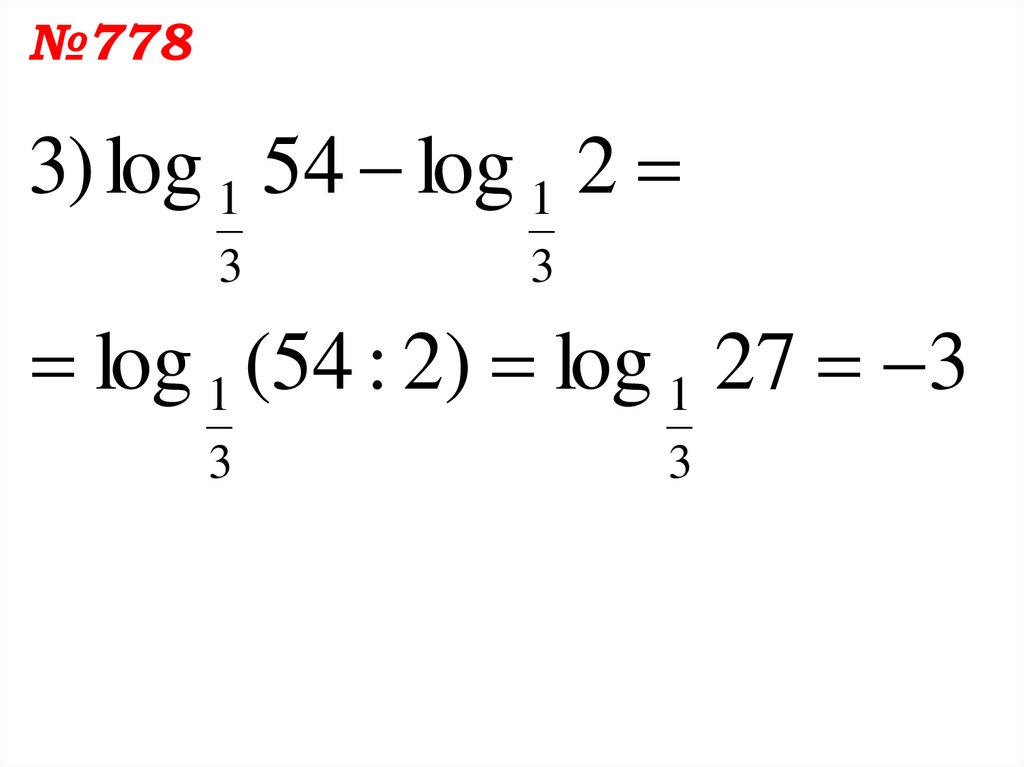
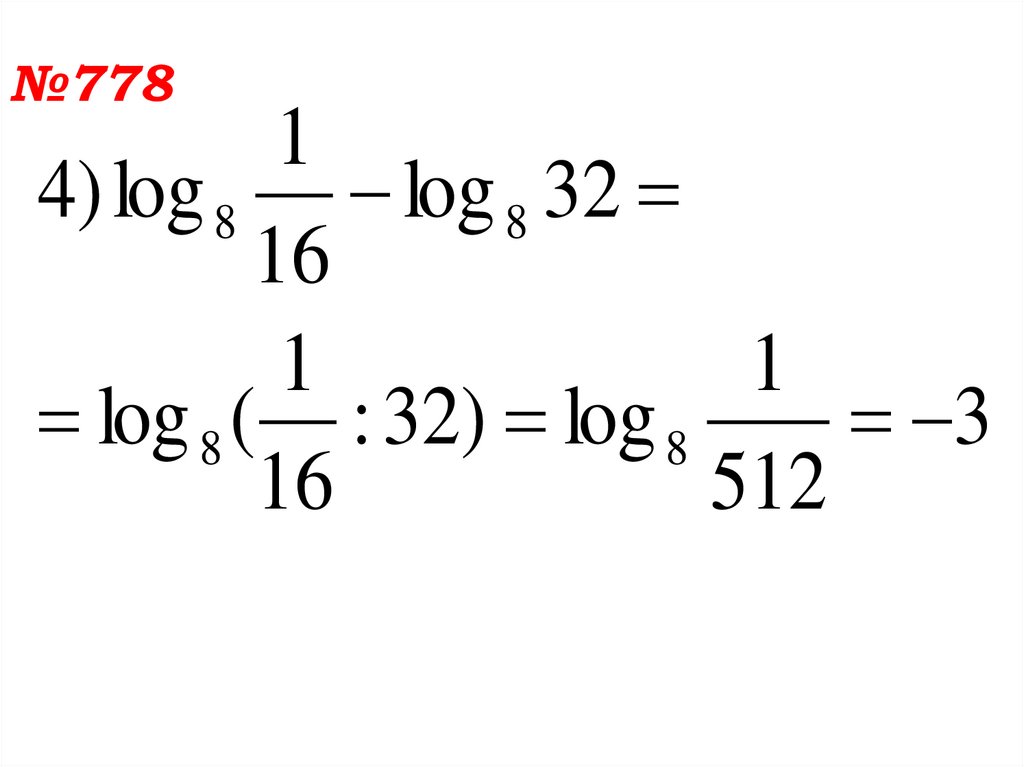

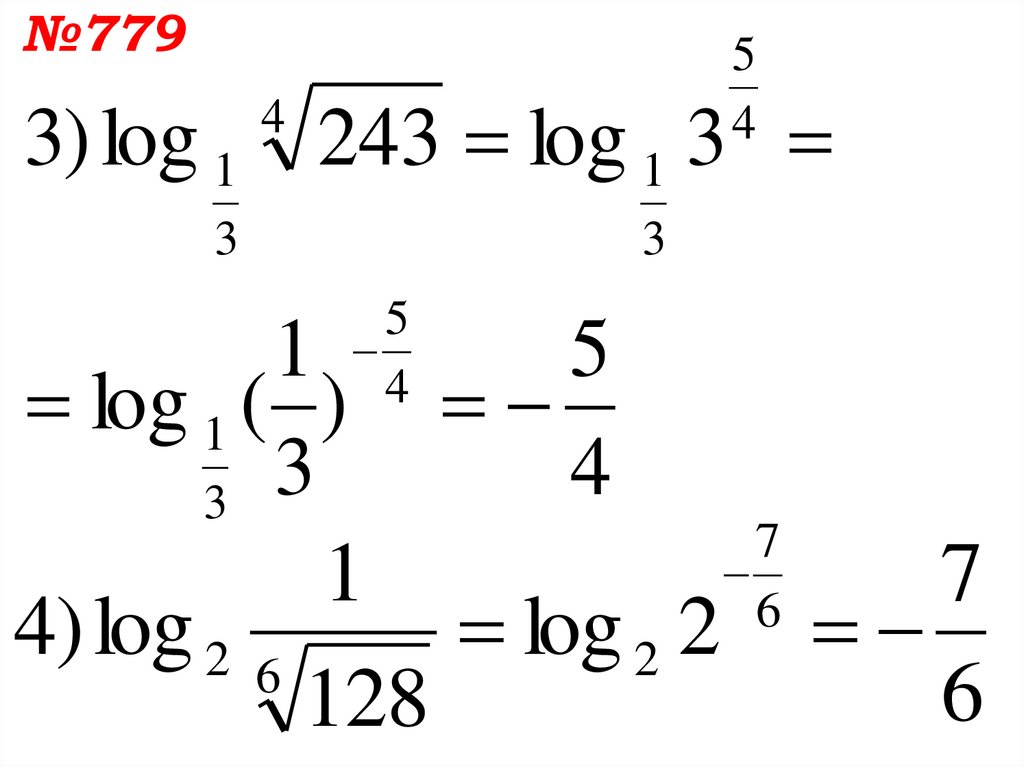
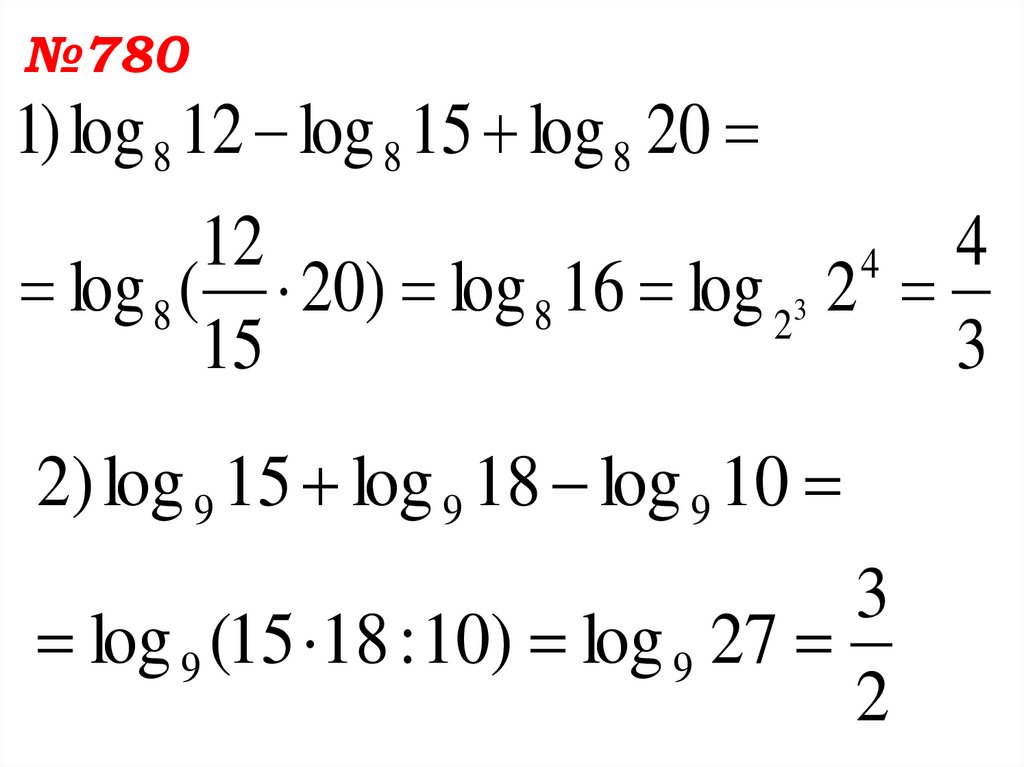
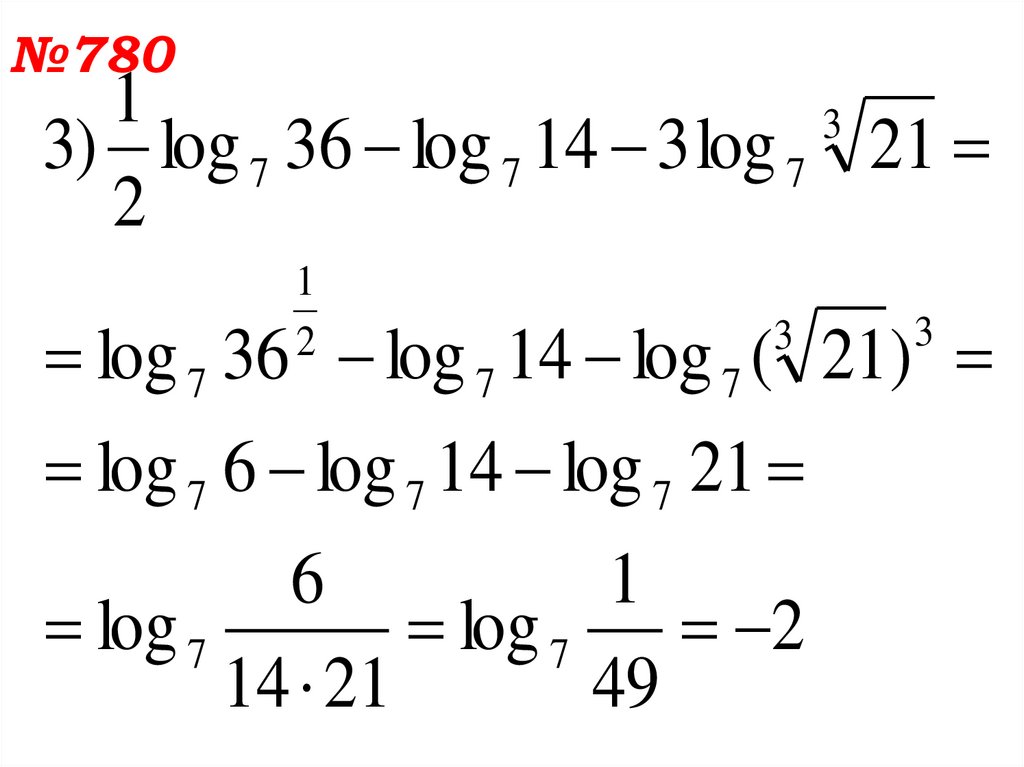
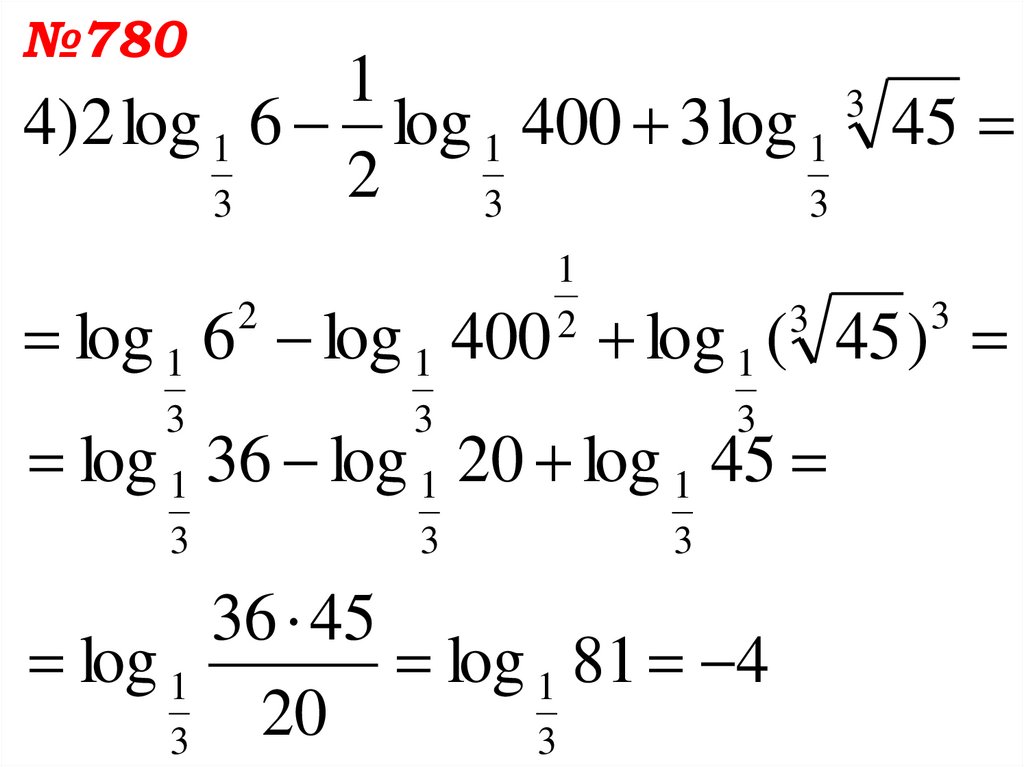
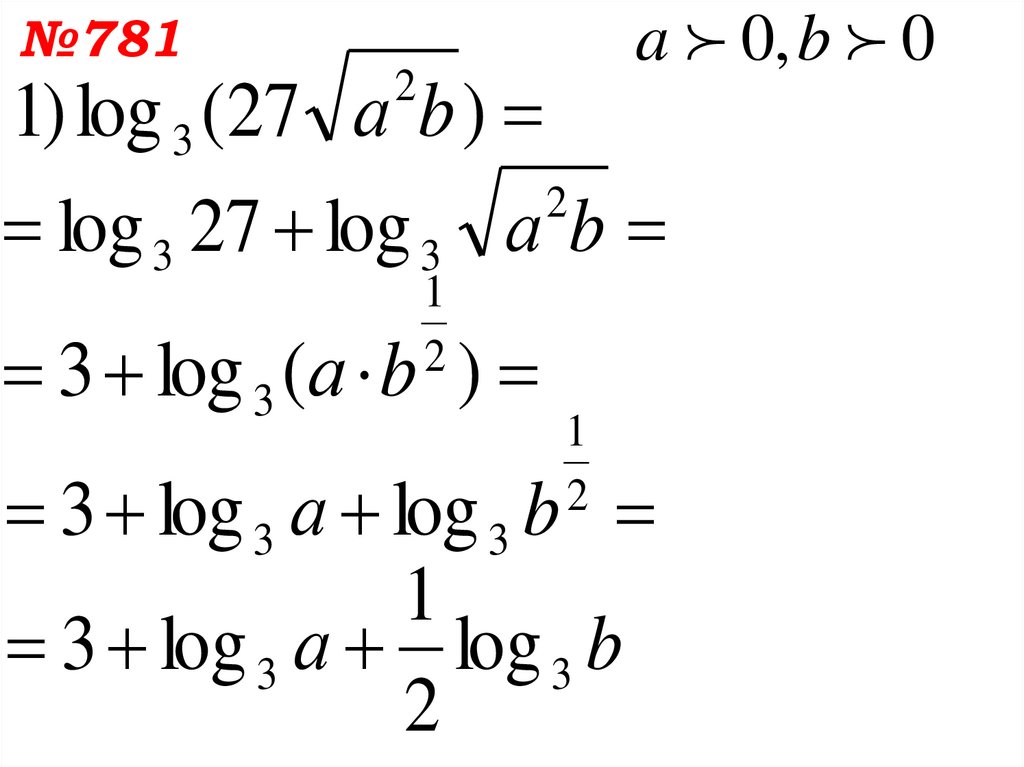
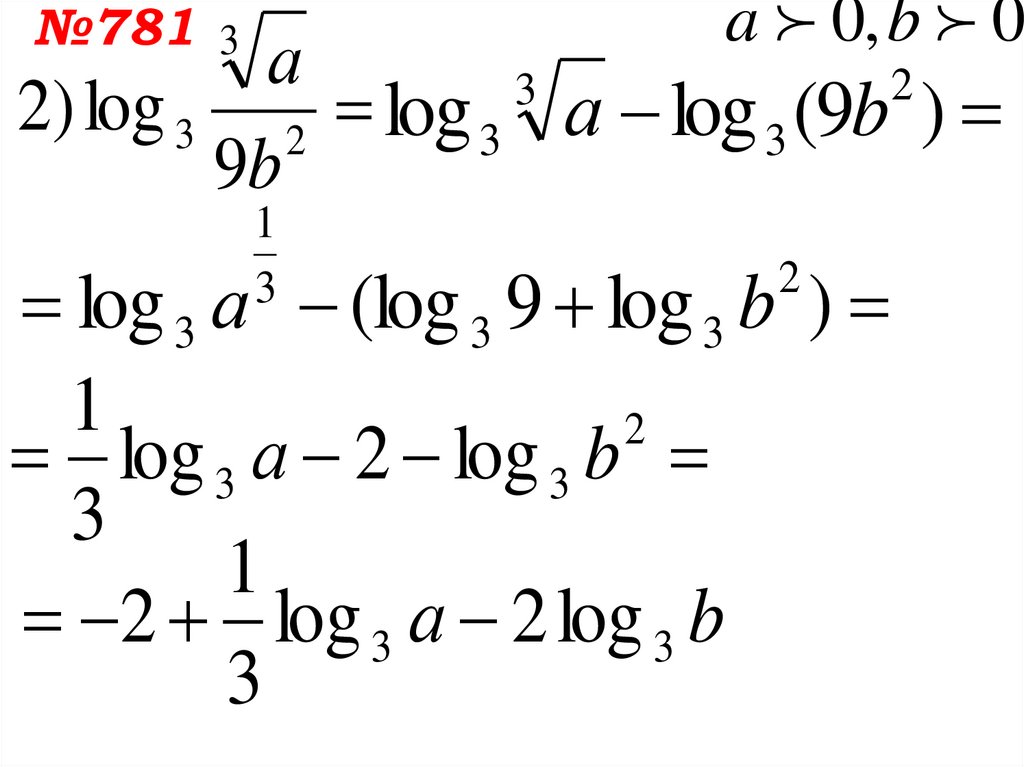
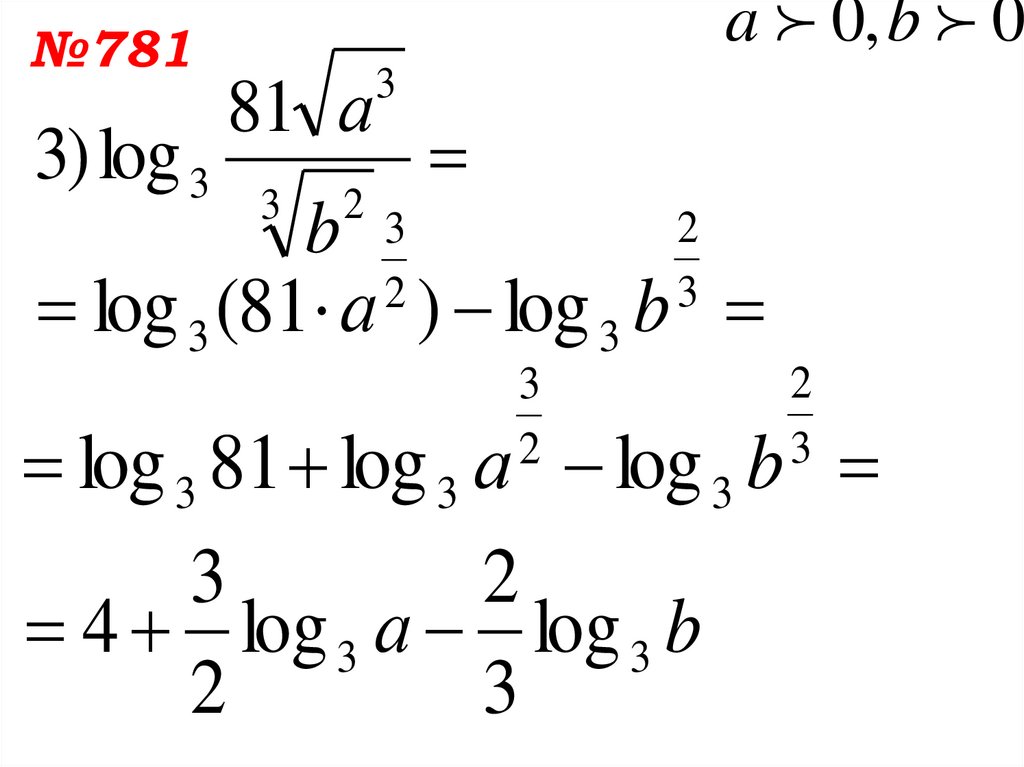

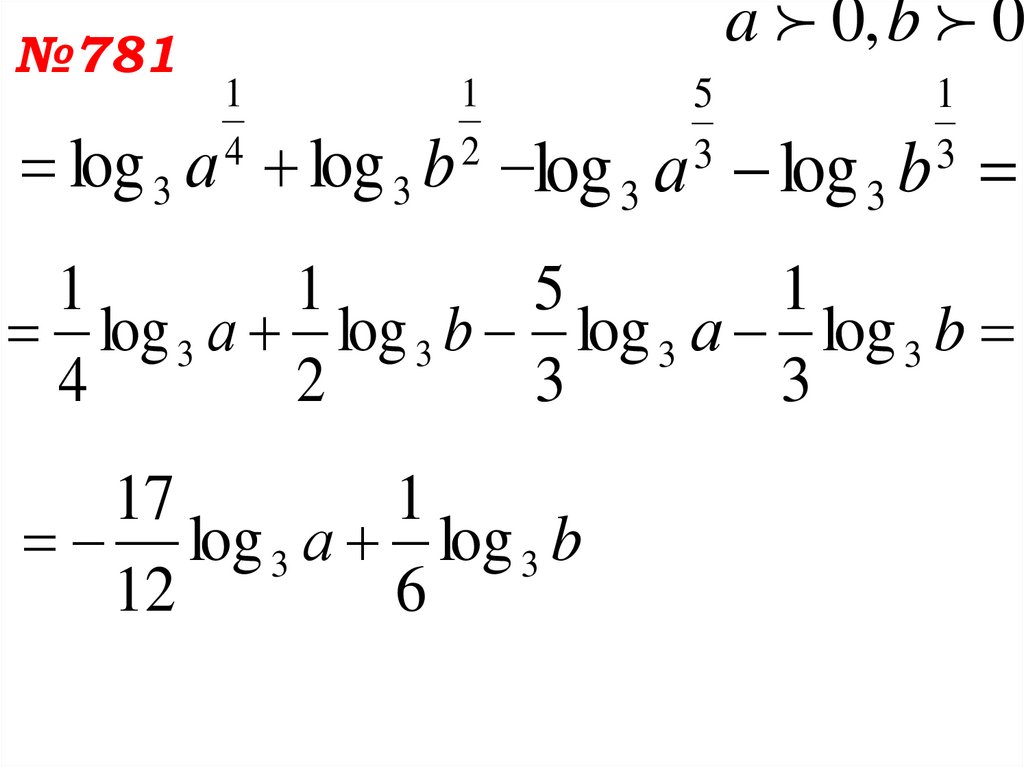




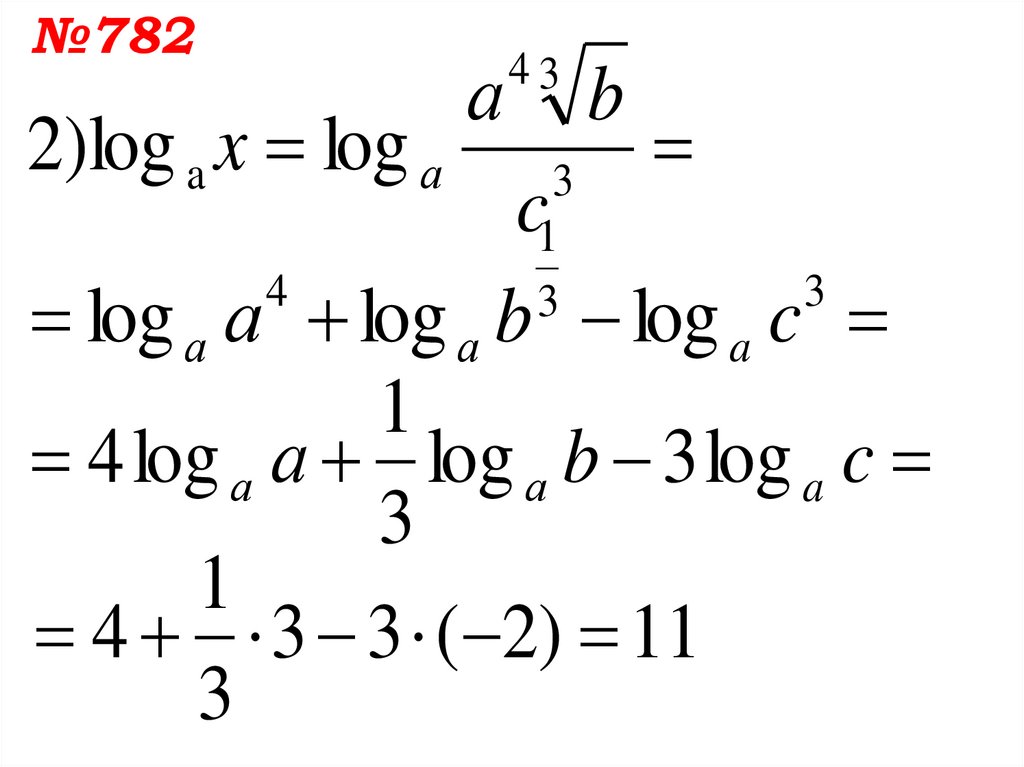
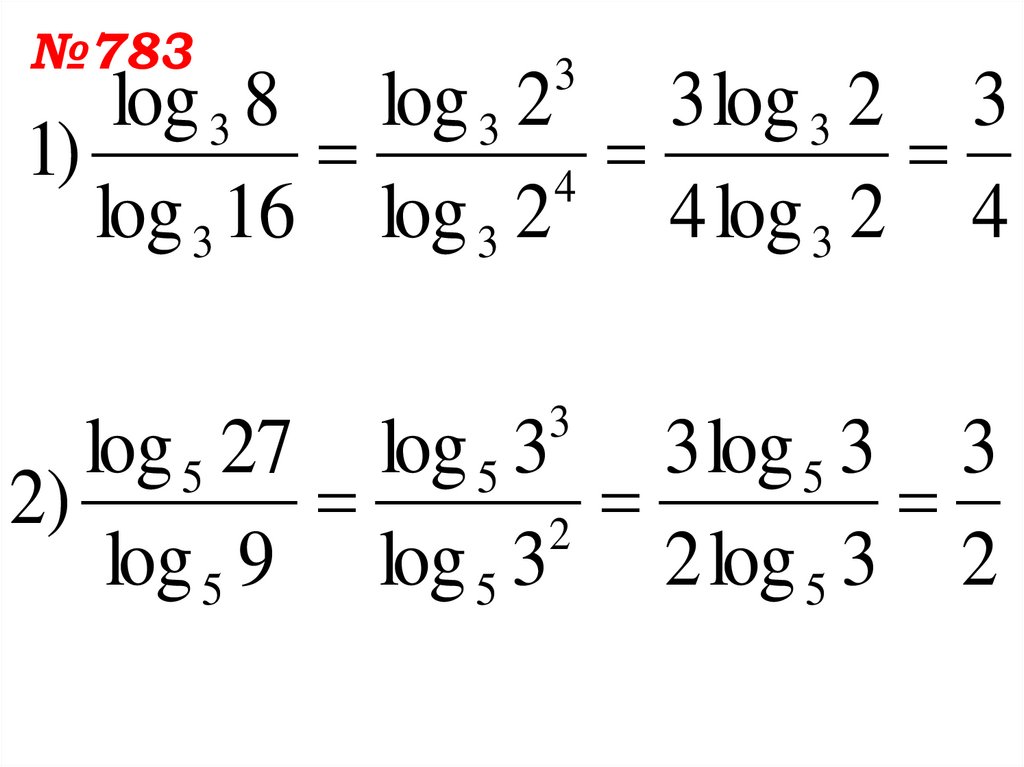












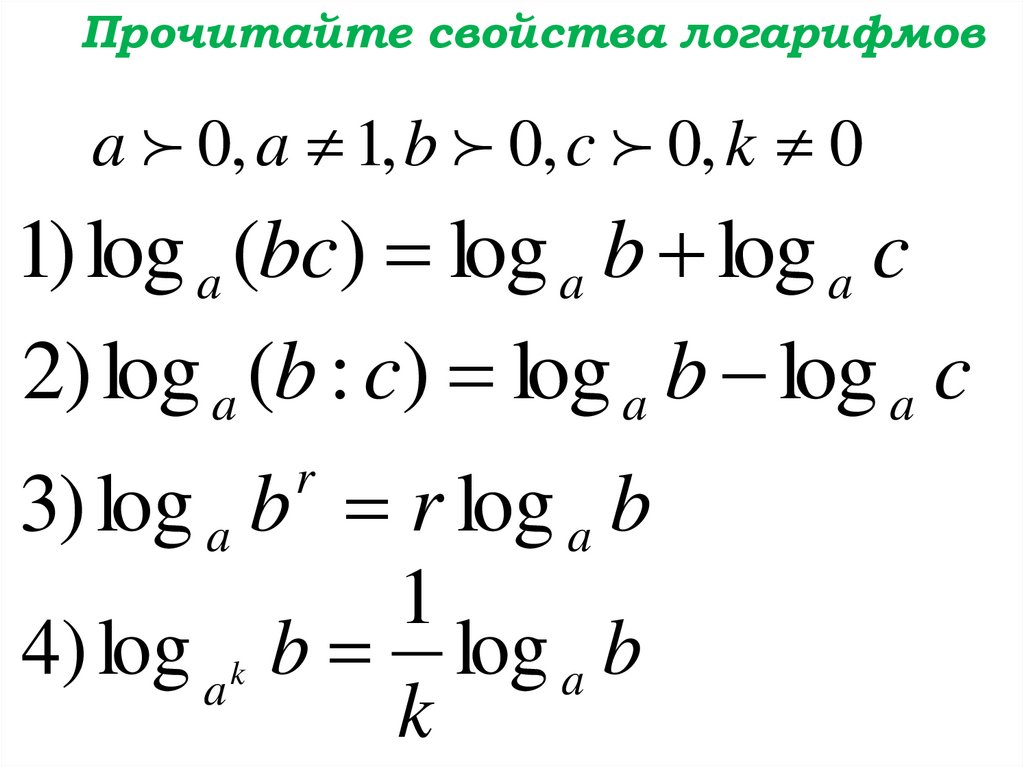

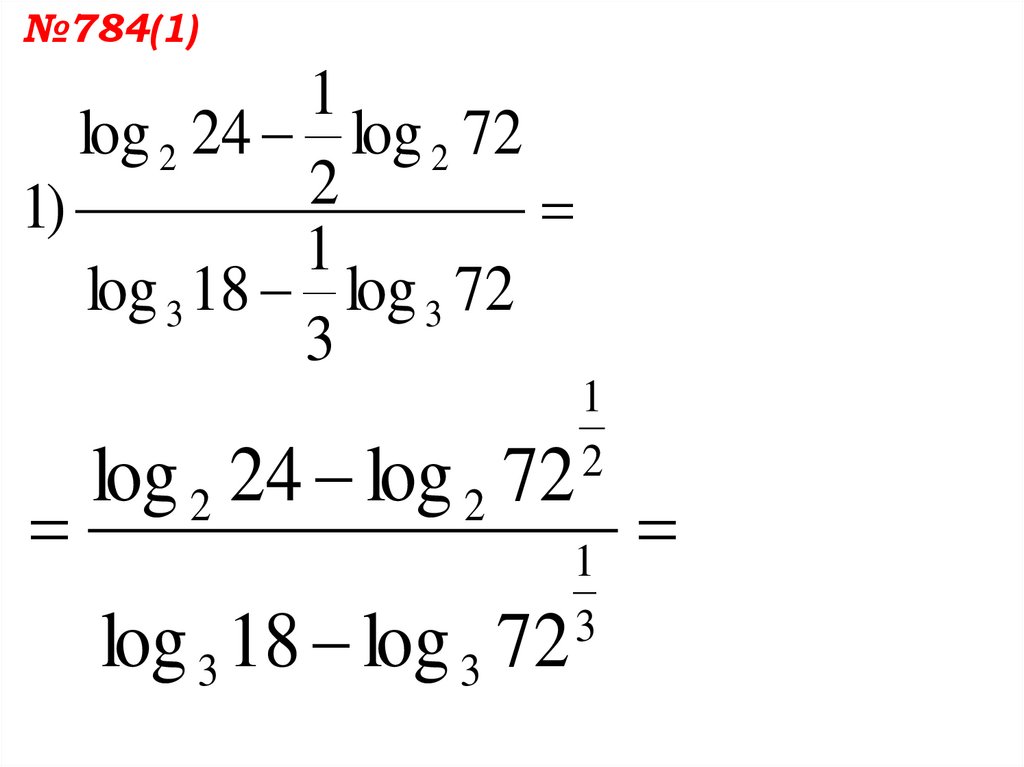

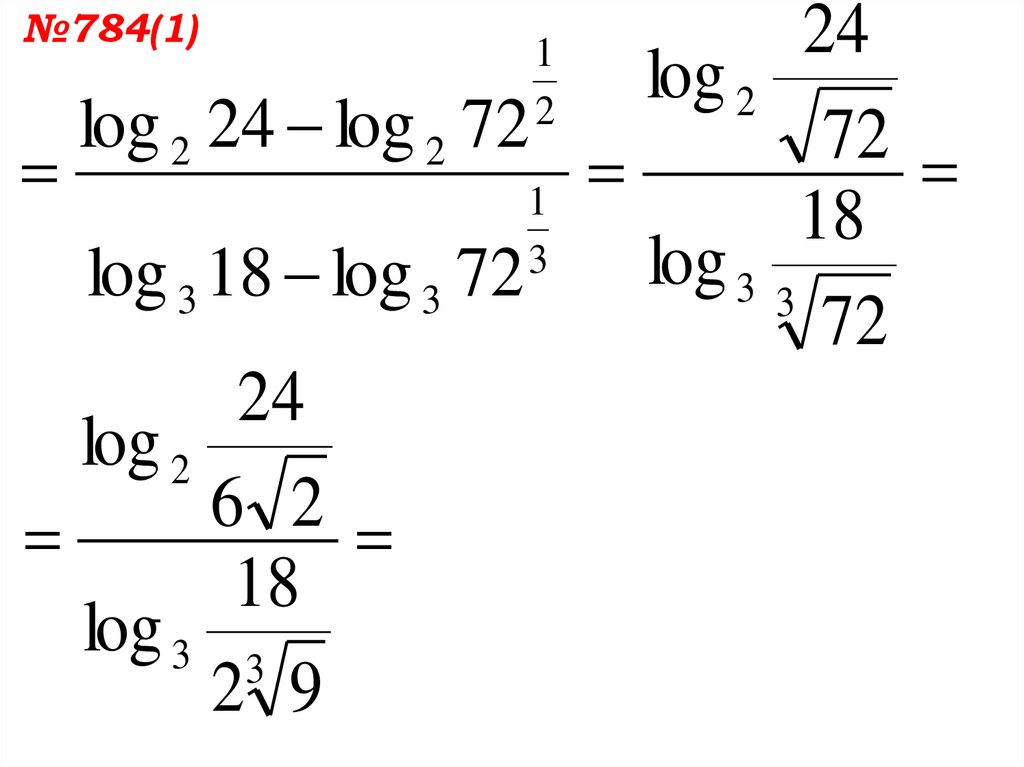
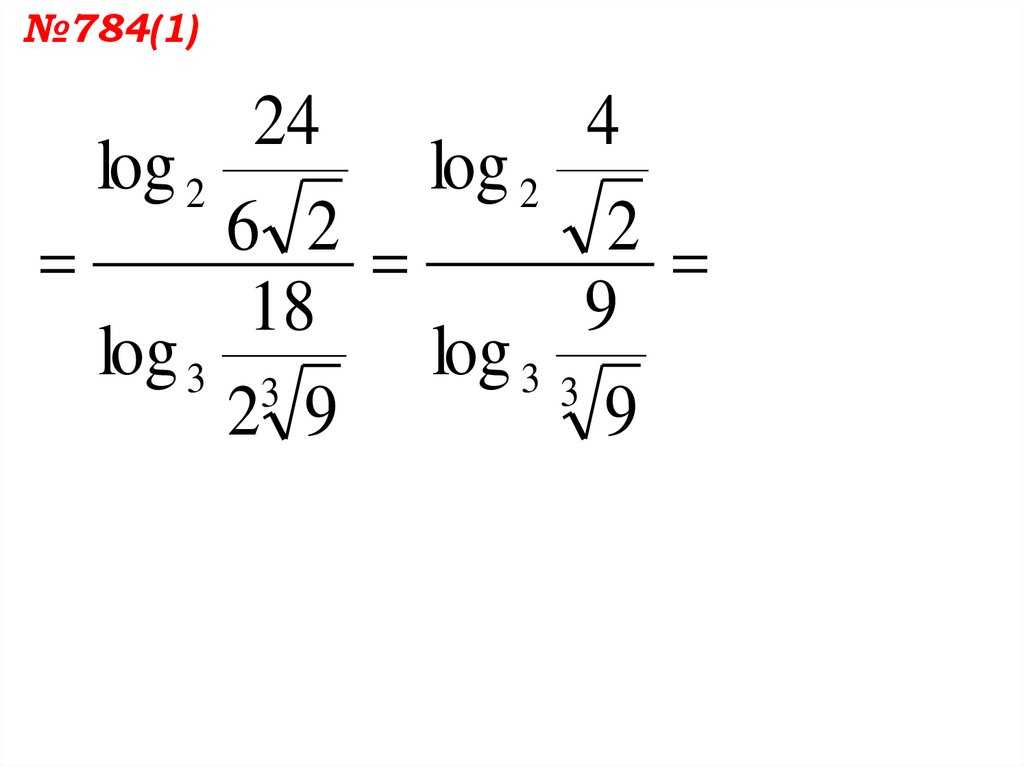


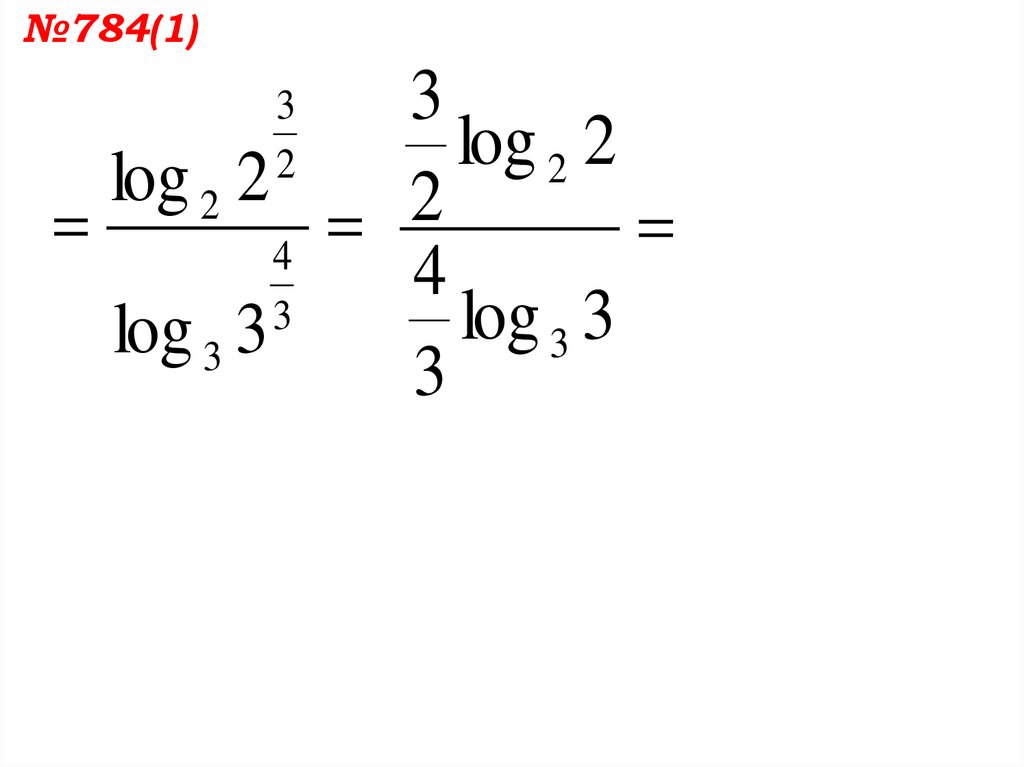







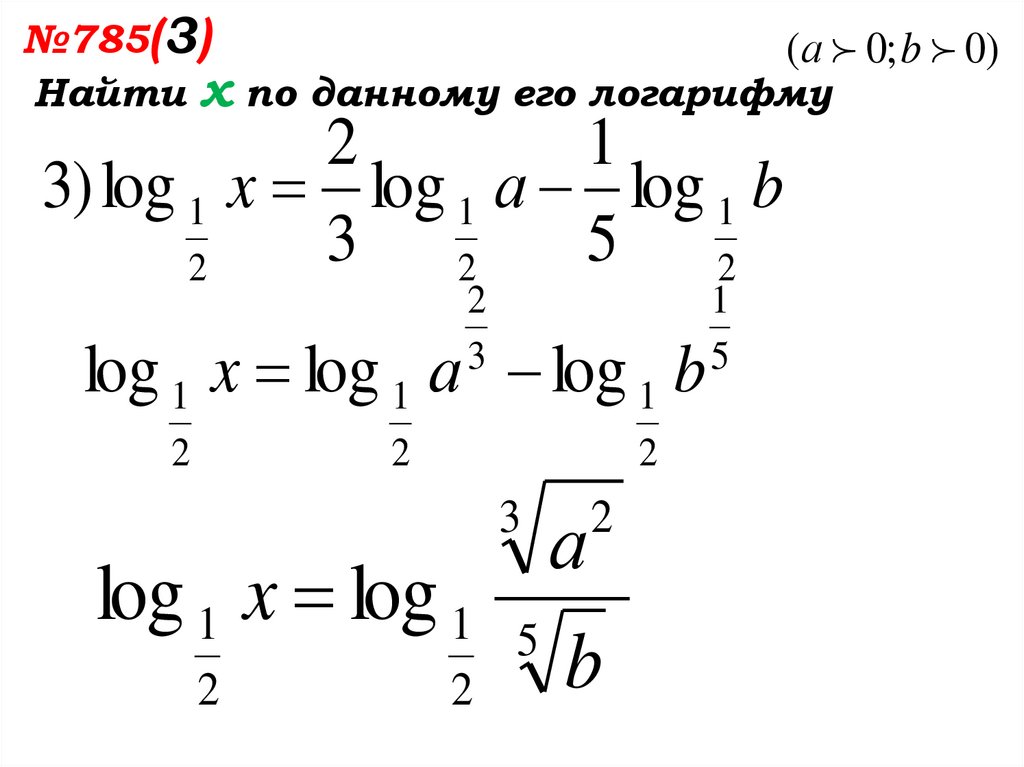

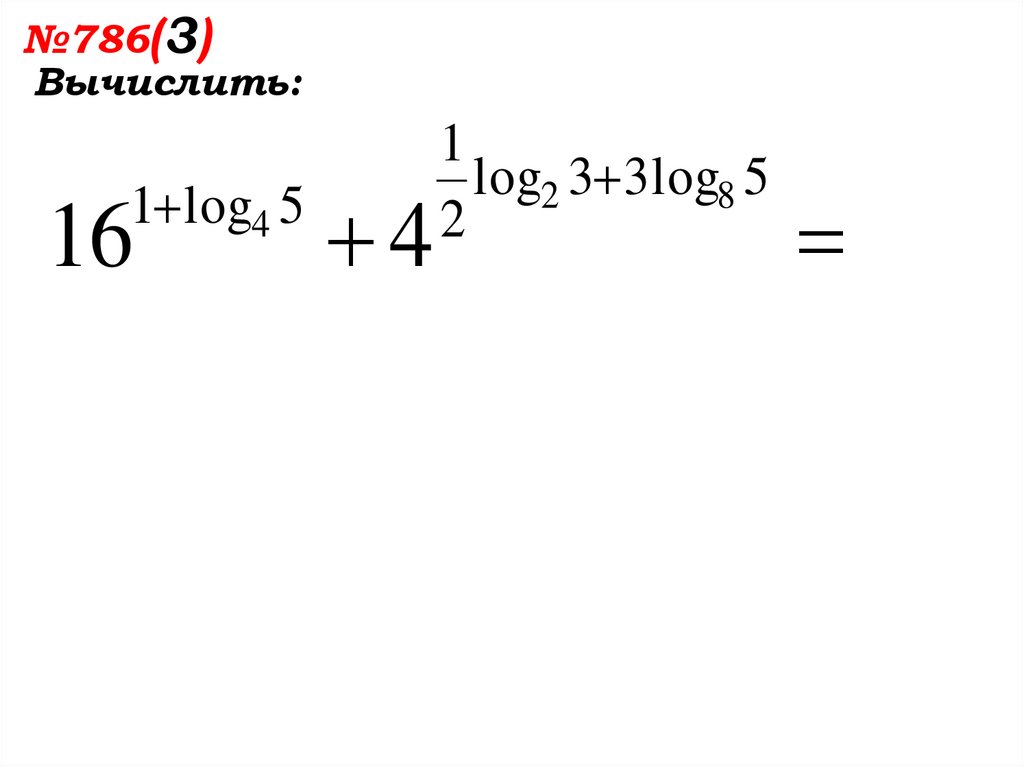
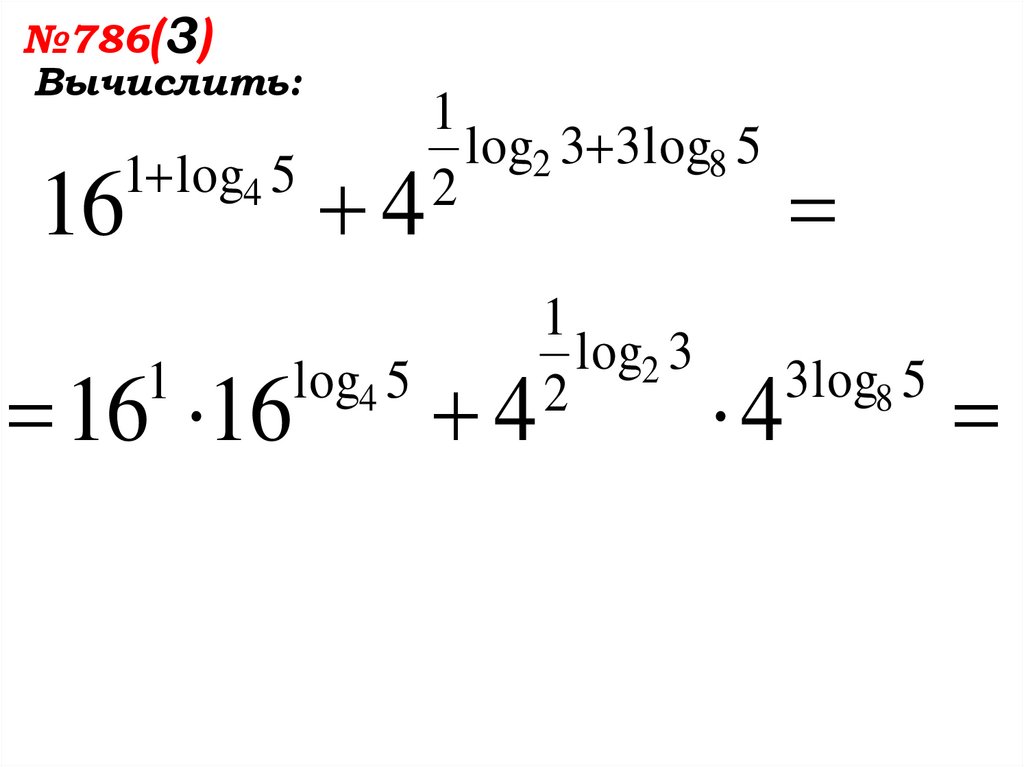


















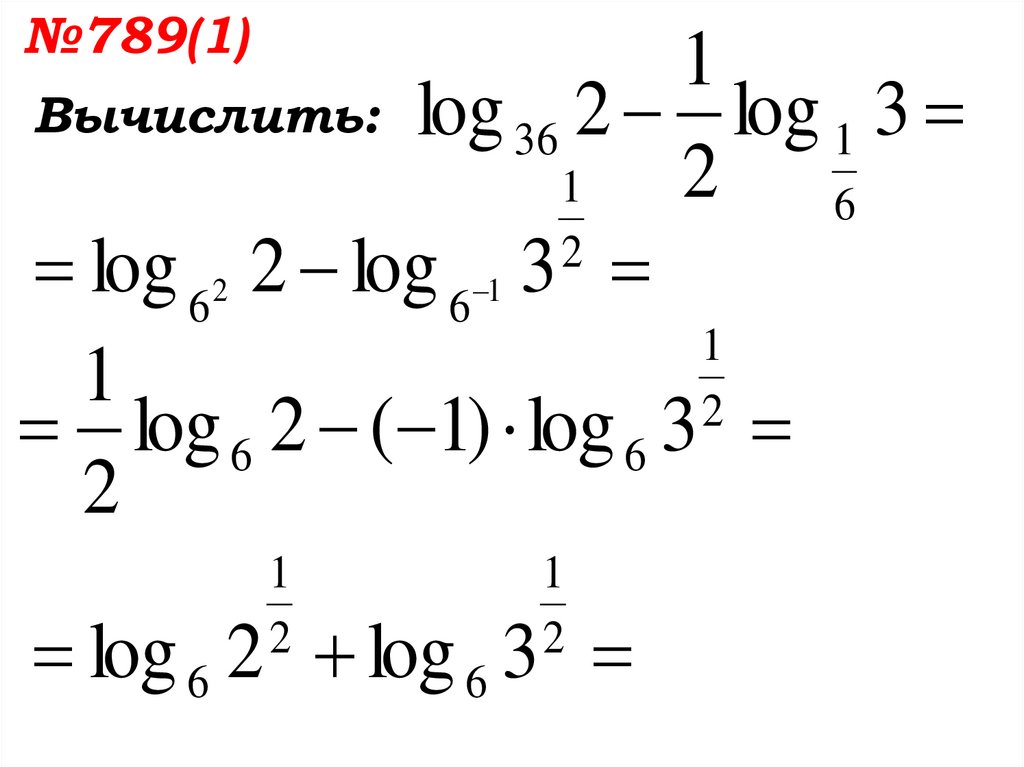

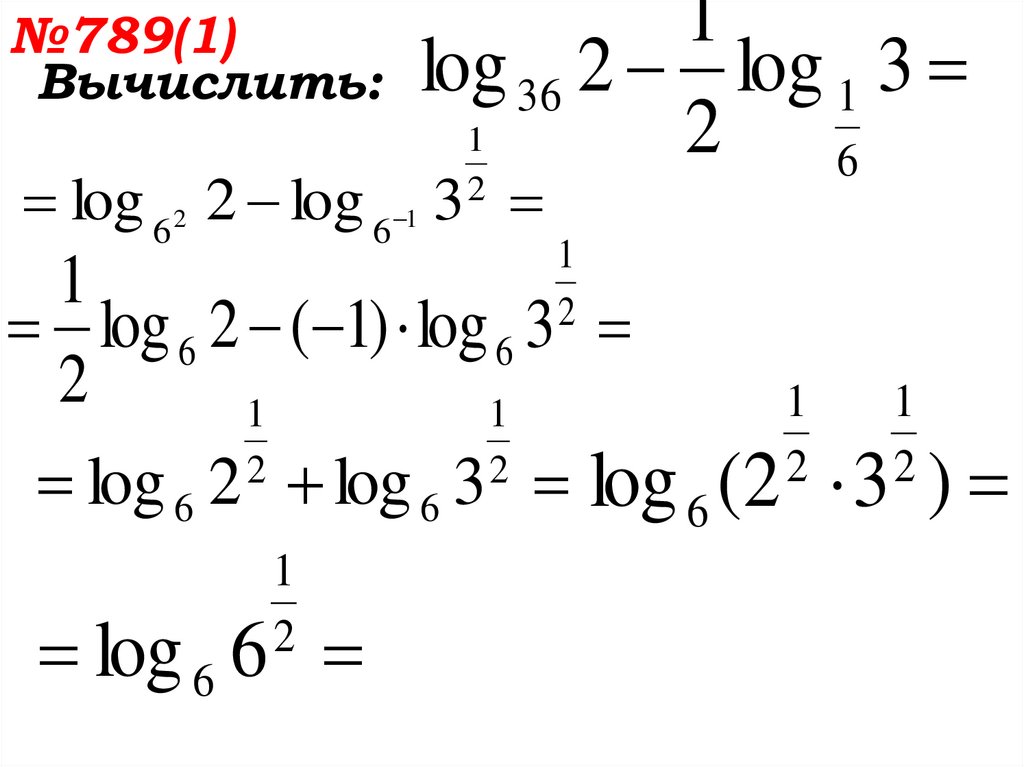
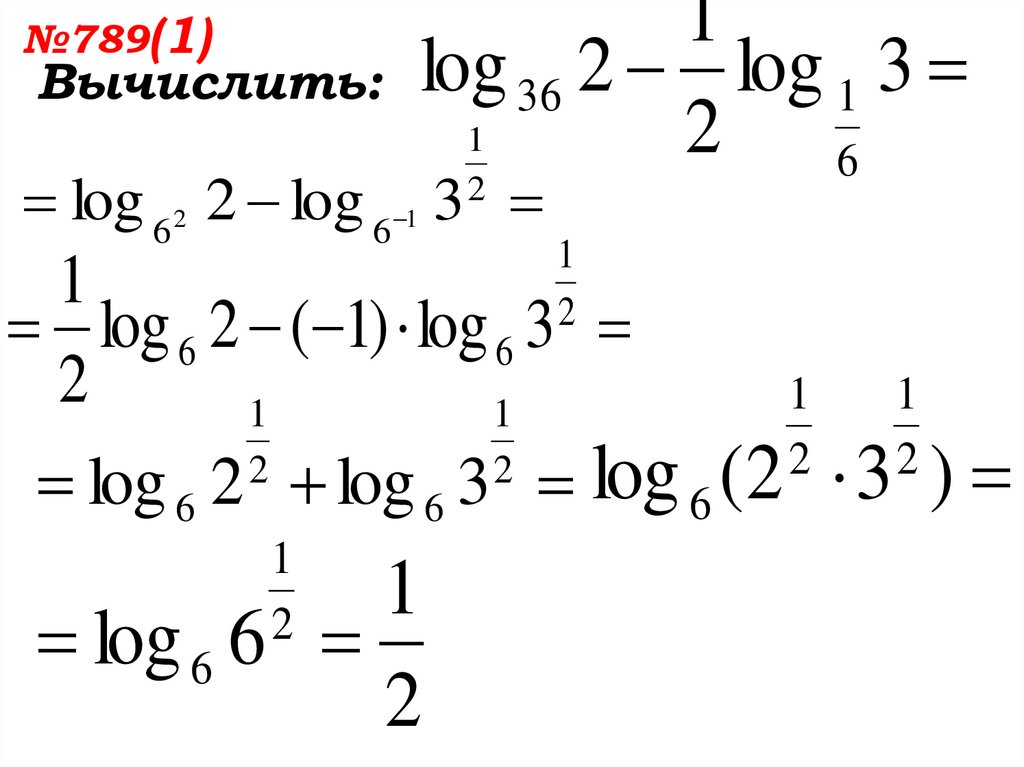
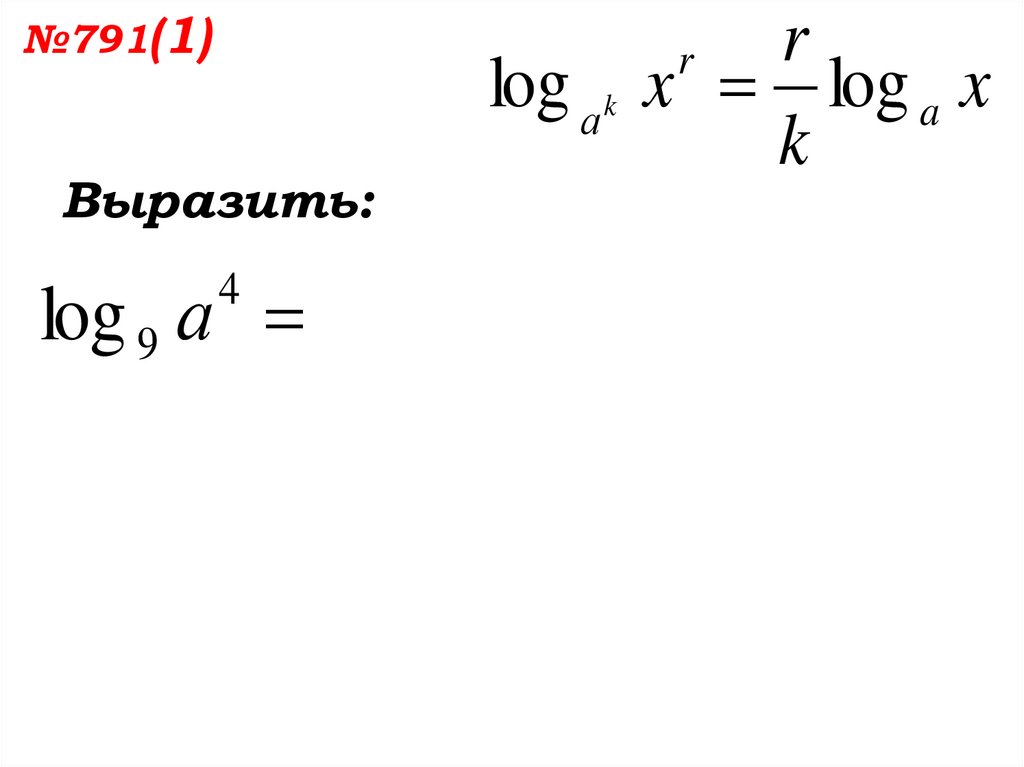
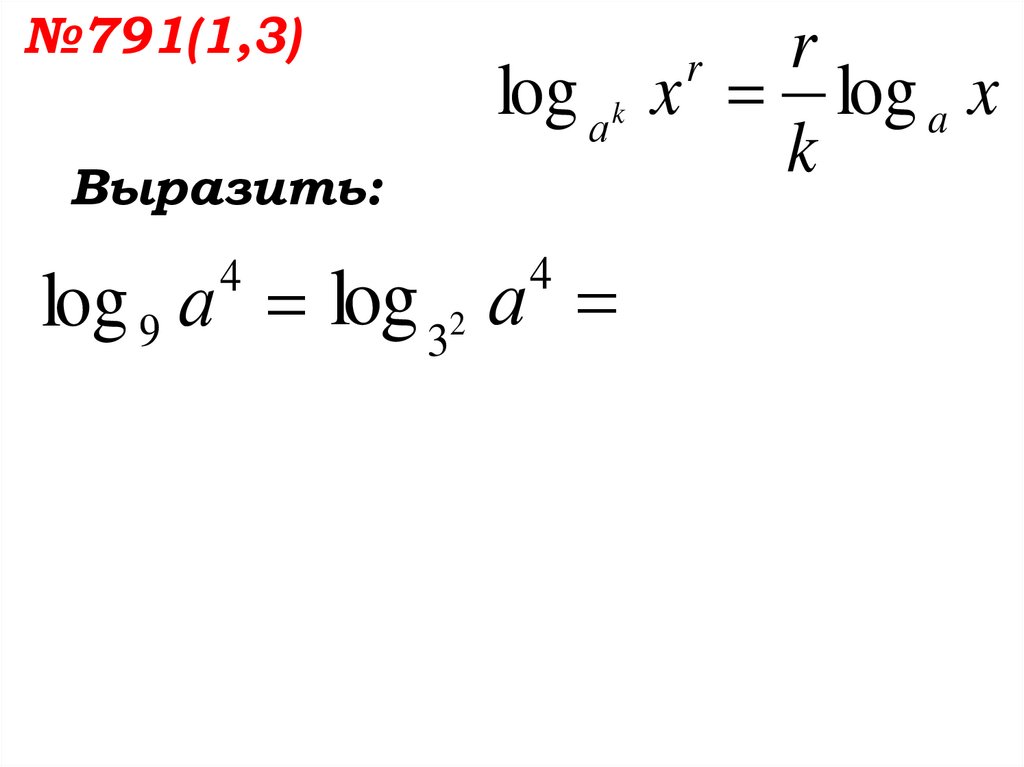
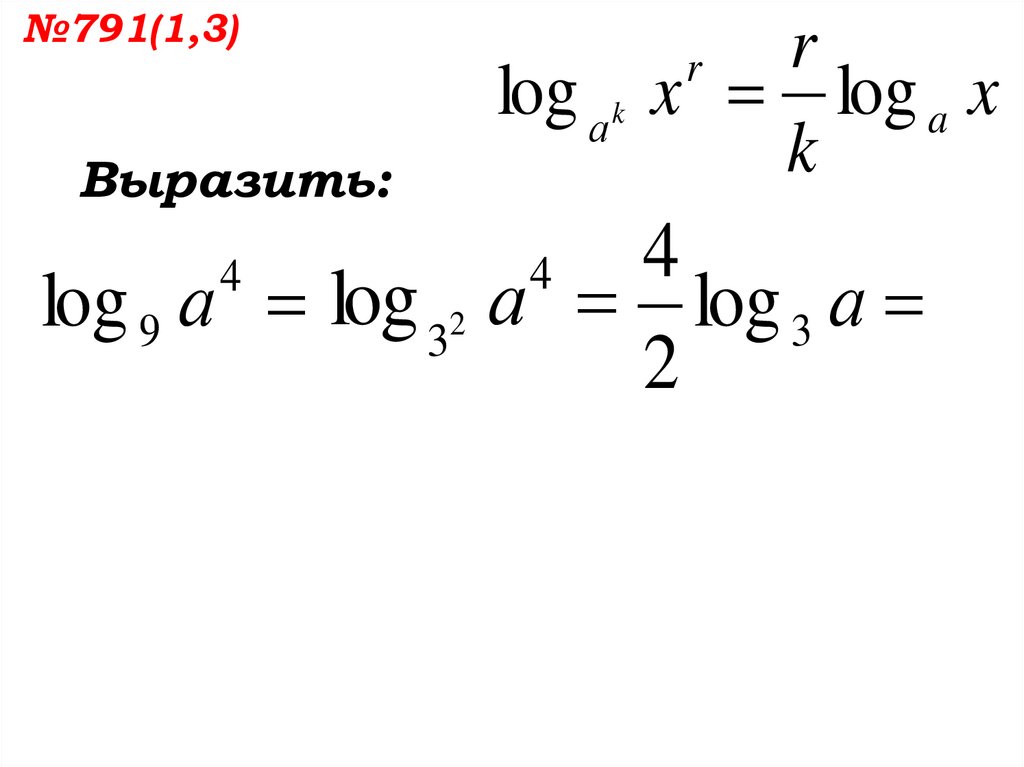
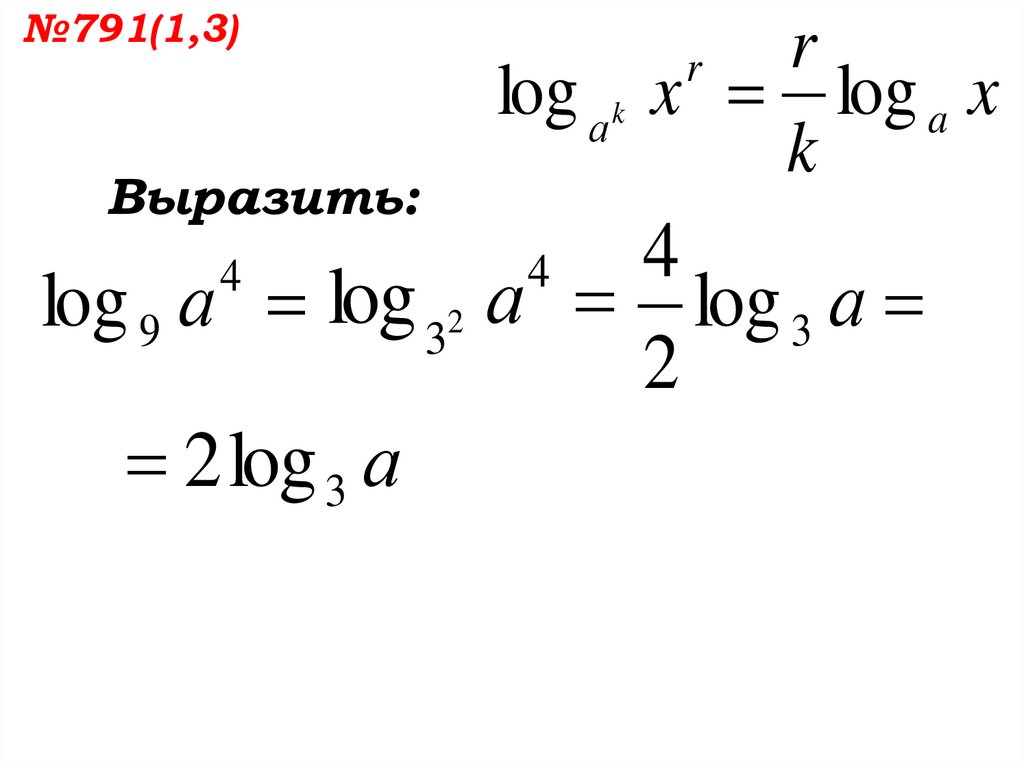

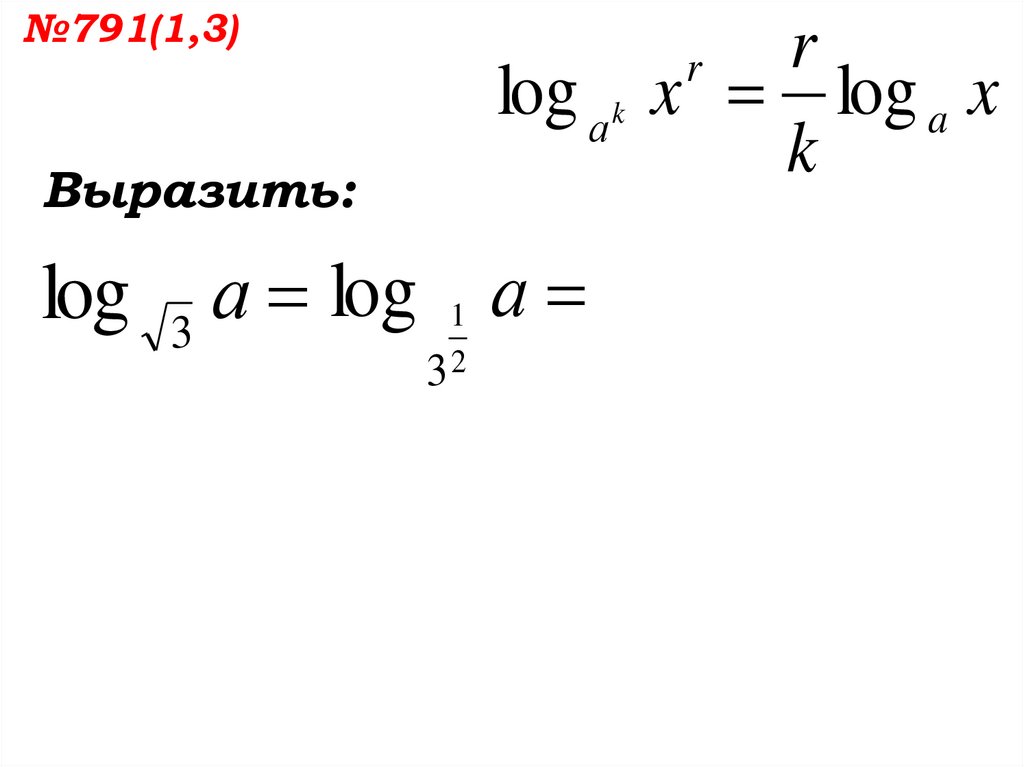















 mathematics
mathematics








