Система обучения алгебре, направленная на формирование функциональной грамотности у обучающихся

1.

СИСТЕМА ОБУЧЕНИЯ АЛГЕБРЕ, НАПРАВЛЕННАЯ НА
ФОРМИРОВАНИЕ ФУНКЦИОНАЛЬНОЙ ГРАМОТНОСТИ У
ОБУЧАЮЩИХСЯ
Все права защищены. Никакая часть презентации не может быть воспроизведена в какой бы то ни было форме и какими бы то ни было средствами, включая размещение в Интернете и в
корпоративных сетях, а также запись в память ЭВМ, для частного или публичного использования, без письменного разрешения владельца авторских прав. © АО «Издательство «Просвещение», 2021 г.

2.

Вопросы для обсуждения на вебинаре
1. Понятие
функциональной
интегративные компоненты.
2. Диагностика
уровня
функциональной грамотности.
грамотности
и
её
сформированности
3. Ключевые аспекты построения системы обучения
алгебре.
4. Примеры формирования функциональной грамотности
средствами алгебры.

3.

1.Понятие функциональной
грамотности и её интегративные
компоненты.

4.

Функциональная грамотность
1965:
Всемирный
конгресс
министров
просвещения в
Тегеране
Под функциональной грамотностью подразумевается «совокупность
умений читать и писать для использования в повседневной жизни и
решения житейских проблем».
1978:
ЮНЕСКО
«функционально грамотным считается только тот, кто может
принимать участие во всех видах деятельности, в которых
грамотность необходима для эффективного функционирования его
группы и которые дают ему также возможность продолжать
пользоваться чтением, письмом и счётом для своего собственного
развития и для дальнейшего развития общины (социального
окружения)».
2002:
ЮНЕСКО
функциональная грамотность – это «…полноценно и эффективно
функционировать как члены сообщества, родители, граждане и
работники».

5.

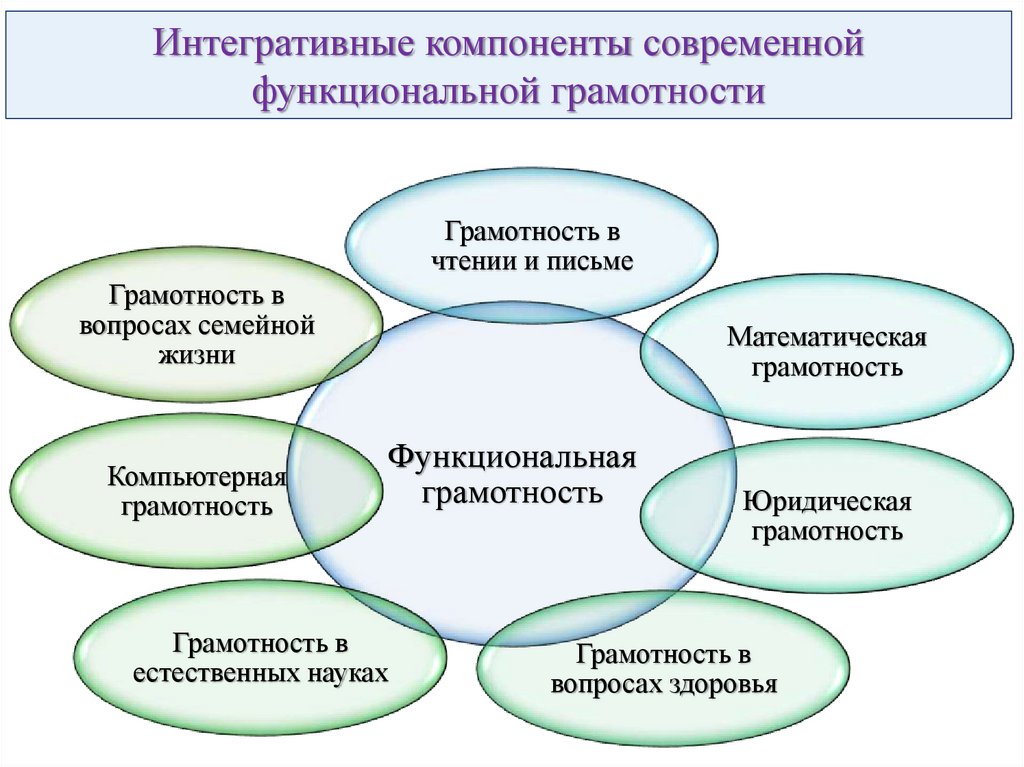
Интегративные компоненты современной
функциональной грамотности
Грамотность в
чтении и письме
Грамотность в
вопросах семейной
жизни
Компьютерная
грамотность
Математическая
грамотность
Функциональная
грамотность
Грамотность в
естественных науках
Юридическая
грамотность
Грамотность в
вопросах здоровья

6.

Под математической грамотностью понимается способность человека
формулировать, применять и интерпретировать математику в разнообразных
ситуациях, использовать математические понятия, методы, факты и инструменты
для описания, объяснения и прогнозирования явлений.
РЕАЛЬНЫЙ МИР
Проблема,
возникшая в
ситуации
Принятие
результатов
Результат в
рамках ситуации
Интерпретация
результатов
Создание модели
Математическая
проблема
Математический
результат
Применение
математики
МАТЕМАТИЧЕСКИЙ МИР
Математическая грамотность помогает человеку понимать роль математики в
мире, высказывать хорошо обоснованные суждения и принимать решения,
необходимые для конструктивного, активного и размышляющего гражданина.

7.

2. Диагностика уровня
сформированности
функциональной грамотности.

8.

Международные исследования. Основные цели
TIMSS
Сделать сравнительную оценку
общеобразовательной
подготовки учащихся средней
школы по математике и
естествознанию в странах с
различными системами
образования, выявление
особенностей образовательных
систем, определяющих
различные уровни достижения
учащихся.
PISA
Выяснить: обладают ли
учащиеся 15-летнего возраста,
получившие обязательное
общее образование, знаниями и
умениями, необходимыми им
для полноценного
функционирования в
современном обществе, т.е. для
решения широкого диапазона
задач в различных сферах
человеческой деятельности,
общения и социальных
отношений.
Оценка математической и естественно-научное грамотности.

9.

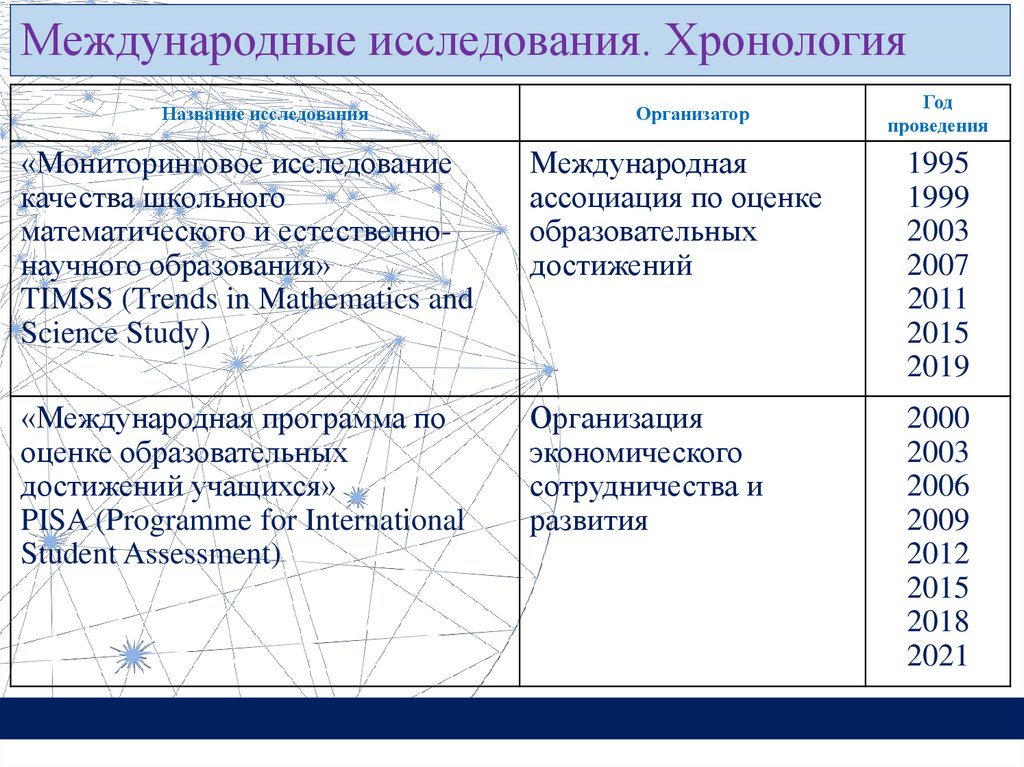
Международные исследования. Хронология
Название исследования
Организатор
Год
проведения
«Мониторинговое исследование
качества школьного
математического и естественнонаучного образования»
TIMSS (Trends in Mathematics and
Science Study)
Международная
ассоциация по оценке
образовательных
достижений
1995
1999
2003
2007
2011
2015
2019
«Международная программа по
оценке образовательных
достижений учащихся»
PISA (Programme for International
Student Assessment)
Организация
экономического
сотрудничества и
развития
2000
2003
2006
2009
2012
2015
2018
2021

10.

Международные исследования. Участники - 2018
Австралия
Австрия
Албания
Алжир
Аргентина
Баку (Азербайджан)
Беларусь
Бельгия
Болгария
Босния и Герцеговина
Бразилия
Бруней-Даруссалам
Великобритания
Венгрия
Вьетнам
Германия
Гонконг
Греция
Грузия
Дания
Доминиканская Республика
Израиль
Индонезия
Иордания
Ирландия
Исландия
Испания
Италия
Казахстан
Канада
Катар
Колумбия
Косово
Коста-Рика
Латвия
Ливан
Литва
Люксембург
Макао (Китай)
Македония
Малайзия
Мальта
Марокко
Мексика
Молдова
Нидерланды
Новая Зеландия
Норвегия
ОАЭ
Панама
Перу
Польша
Португалия
Республика Корея
Российская Федерация
Румыния
Саудовская Аравия
Сербия
Сингапур
Словацкая Республика
Словения
США
Таиланд
Тайвань
Тринидад и Тобаго
Турция
Украина
Уругвай
Филиппины
Финляндия
Франция
Хорватия
Черногория
Чешская Республика
Чили
Швейцария
Швеция
Шотландия
Эстония
Япония

11.

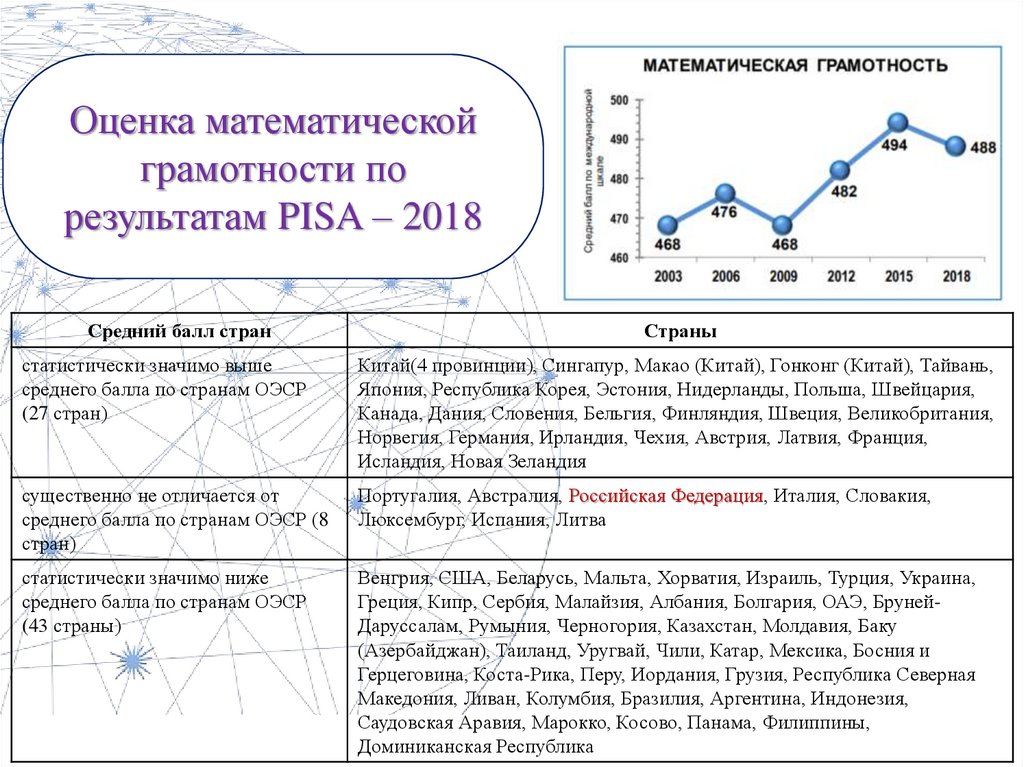
Оценка математической
грамотности по
результатам PISA – 2018
Средний балл стран
Страны
статистически значимо выше
среднего балла по странам ОЭСР
(27 стран)
Китай(4 провинции), Сингапур, Макао (Китай), Гонконг (Китай), Тайвань,
Япония, Республика Корея, Эстония, Нидерланды, Польша, Швейцария,
Канада, Дания, Словения, Бельгия, Финляндия, Швеция, Великобритания,
Норвегия, Германия, Ирландия, Чехия, Австрия, Латвия, Франция,
Исландия, Новая Зеландия
существенно не отличается от
среднего балла по странам ОЭСР (8
стран)
Португалия, Австралия, Российская Федерация, Италия, Словакия,
Люксембург, Испания, Литва
статистически значимо ниже
среднего балла по странам ОЭСР
(43 страны)
Венгрия, США, Беларусь, Мальта, Хорватия, Израиль, Турция, Украина,
Греция, Кипр, Сербия, Малайзия, Албания, Болгария, ОАЭ, БрунейДаруссалам, Румыния, Черногория, Казахстан, Молдавия, Баку
(Азербайджан), Таиланд, Уругвай, Чили, Катар, Мексика, Босния и
Герцеговина, Коста-Рика, Перу, Иордания, Грузия, Республика Северная
Македония, Ливан, Колумбия, Бразилия, Аргентина, Индонезия,
Саудовская Аравия, Марокко, Косово, Панама, Филиппины,
Доминиканская Республика

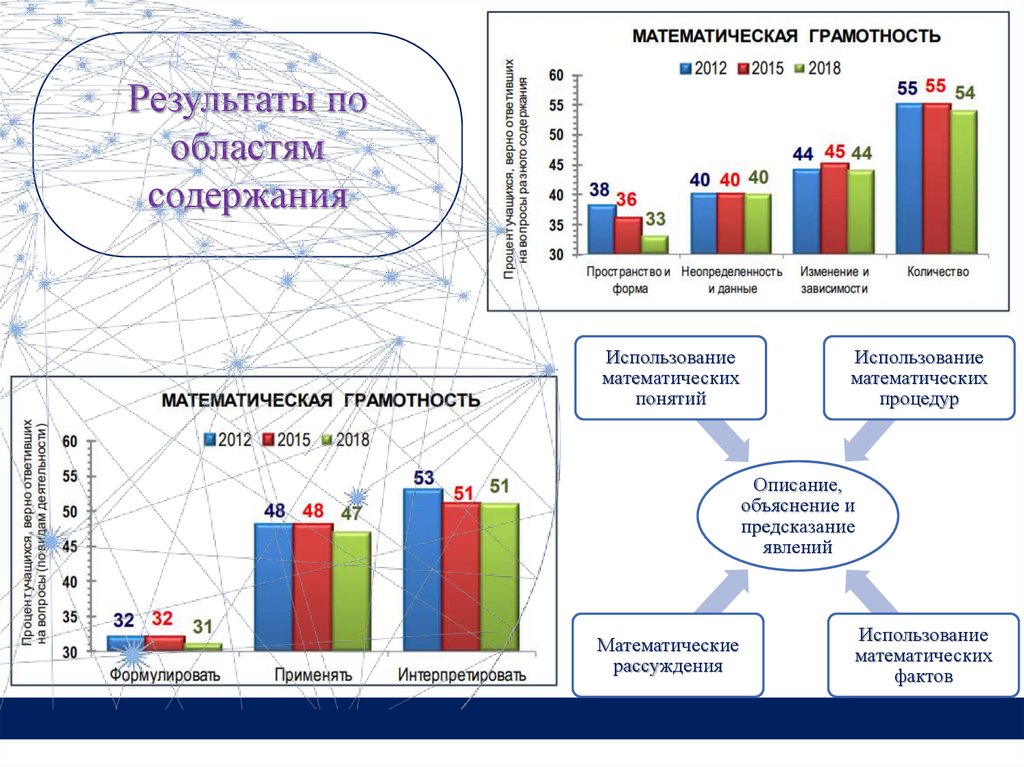
12.

Результаты по
областям
содержания
Использование
математических
понятий
Использование
математических
процедур
Описание,
объяснение и
предсказание
явлений
Математические
рассуждения
Использование
математических
фактов

13.

Уровни математической грамотности PISA
М
Ч
Е
669 708
6 - самостоятельно мыслящие и
5 – 6 708
уровни
способные функционировать в сложных
607 626
633 5
условиях
545 553
559 –4проявляется способность использовать имеющиеся
4 уровень
знания и умения для получения новой информации
482 480 484 3
2 уровень
пороговый, при достижении которого учащиеся начинают
420 407
409 – 2
демонстрировать применение знаний и умений в простейших не
учебных
358 335
335ситуациях
1

14.

15.

16.

17.

18.

Выводы экспертов о математическом образовании в мире
Приоритетная цель – формирование математической грамотности в
системе общего образования
Основные тенденции в математическом образовании стран:
− повышение средних результатов;
− стремление к достижению самых высоких результатов;
− интенсивная работа с отстающими;
− анализ сильных и слабых сторон преподавания математики;
− обеспечение равных возможностей для обучения мальчиков и
девочек.
Выводы экспертов о направлении развития
математического образования
−
−
−
−
погружение учащихся в реальные ситуации;
осознание моделирования как стратегии, которой надо обучать;
формирование метапредметных результатов обучения;
решение задач разными способами и максимальная
независимость учащихся в решении задач.

19.

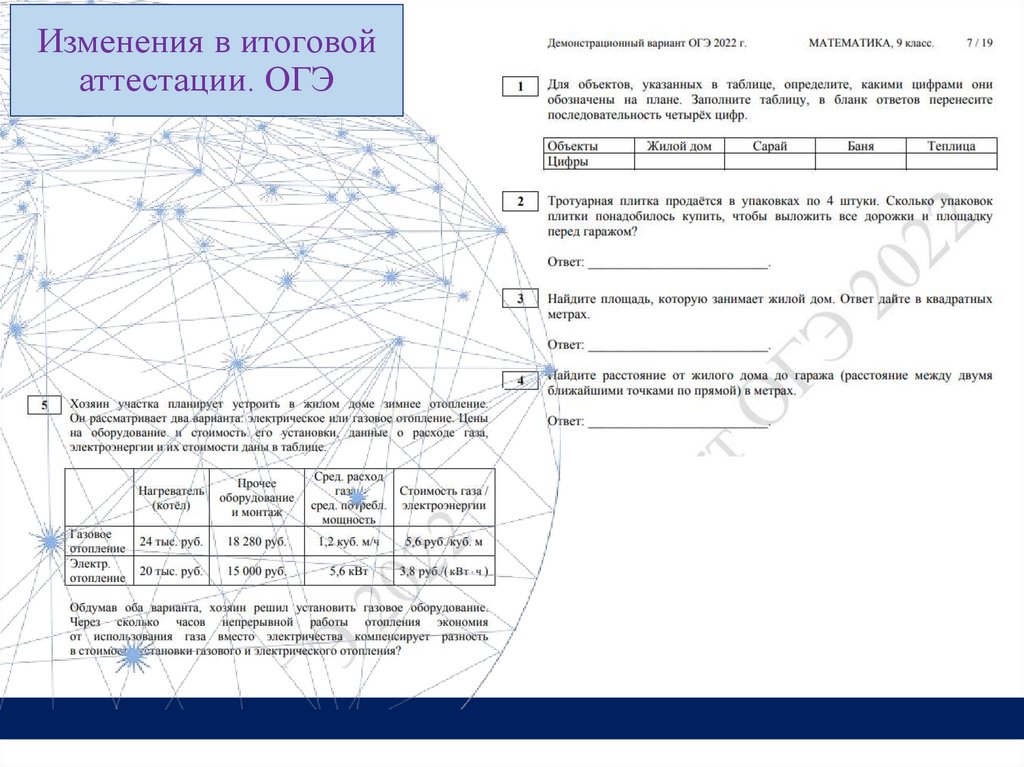
Изменения в итоговой
аттестации. ОГЭ

20.

Изменения в итоговой
аттестации. ОГЭ

21.

Изменения в итоговой
аттестации. ЕГЭ

22.

Эффект типичной задачи
− Решая типичную текстовую задачу, ученик подменяет этап понимания и
составления модели категоризацией и поиском в памяти готового алгоритма
для данной категории задач, моделирование подменяется поиском готовой
модели.
− При решении нетипичной задачи этапы понимания развернуты,
самостоятельны, этап интерпретации логичен и осмыслен.
Пример нетипичной задачи
Размер велосипедного колеса (по
внешнему диаметру покрышки)
традиционно указывается в дюймах:
16", ..., 26", 27,5", 28", 29", 36".
На фото: колесо диаметром 26
(слева) и 29" (справа).
Пример типичной задачи
Размер колеса шоссейного велосипеда
равен 27 дюймам. Чему равен размер
обода такого колеса в сантиметрах, если
1 дюйм равен примерно 2,54 см?
Планируемый результат:
вычислять длину окружности в
заданных единицах измерения,
выполняя перевод одних единиц в
другие, исходя из имеющейся
справочной информации, округлять.

23.

3. Ключевые аспекты построения
системы обучения алгебре.

24.

Авторы:
Мордкович А.Г., Семенов П.В.,
Александрова Л.А., Мардахаева Е.Л.
Алгебра, 7-9 классы
Математика – это язык, на котором
говорят все точные науки.
Н.И.Лобачевский
Класс
Алгебра и начала математического анализа, 10-11 классы
Функция
Реальные и физические процессы
7 класс
Линейная функция.
Равномерные процессы.
8 класс
Квадратичная функция. k
y x, y
Функции
x
Равноускоренные процессы.
9 класс
и
y x.
3
3
Функции y x и y x .
Обобщение изученного в основной школе, формализация некоторых определений и
понятий.
10 класс Тригонометрические функции.
Периодические
процессы,
гармонические колебания.
Степенные, показательные и логарифмические Процессы органического роста.
функции.
11 класс Элементы теории пределов, дифференциального
и интегрального исчисления; обобщение
изученного.
Мгновенная скорость, площадь и
объём, оптимальные значения
некоторых величин.

25.

Примерное планирование
пп
Тема
Глава 1. Математический язык. Математические модели.
1 Числовые и алгебраические выражения.
Кол-во часов
17
3
2
Понятие о математическом языке.
2
3
Свойства степеней с натуральными показателями.
3
4
Понятие о математических моделях.
2
5
Линейные уравнения с одной переменной.
3
6
Координатная прямая.
1
7
Числовые промежутки на координатной прямой.
2
Контрольная работа № 1.
1
Глава 2. Линейная функция.
13
8
Координатная плоскость. Координаты точки на плоскости.
1
9
Координатная плоскость. Построение точки на плоскости по
заданным координатам.
1

26.

Актуализация знаний из курса Математики
5-6-х классов

27.

Детальное изучение процесса составления
математической модели

28.

Обогащение математического языка

29.

Изучение метода математического
моделирования – как основного метода
познания

30.

Использование метода математического
моделирования в различных сюжетных
ситуациях

31.

Практико-ориентированное содержание
задач

32.

Анализ математических моделей

33.

Подробные тексты ориентированы на
самостоятельную работу обучающихся с
текстом.

34.

4. Примеры формирования
функциональной грамотности
средствами алгебры.

35.

Составление схемы определения понятия
–
–
–
–
–
назвать имя понятия – термин;
выявить ближайшее родовое понятие;
выявить признаки понятия – видовые отличия;
сформулировать определение понятия;
привести примеры объектов, входящих в объём понятия.
Состав действия «анализ, синтез»
– выделить объект анализа;
– выявить компонентный состав изучаемого объекта – его составные части
(признаки, свойства, количественные и качественные отношения, частные
случаи, пространственные отношения компонентов объекта);
– исследовать (изучить) отдельно каждый элемент, установить причинноследственные отношения между ними;
– если необходимо, включить изучаемый объект в причинно-следственные
отношения с другими объектами;
– составить план исследования (изучения) объекта в целом – синтез.

36.

Схема определения понятия
Числовое выражение:
1. запись
2. составлена из чисел
3. знаков арифметических действий
4. со смыслом
и
и
и
Алгебраическое выражение:
1. запись
2. составлена из чисел
3. букв
4. знаков арифметических действий
5. со смыслом
и
и
и

37.

Схема определения понятия
Определение ближайшего родового понятия.
Выделение видовых отличий.
Структурирование информации.
Линейное уравнение с одной переменной:
1) уравнение
и
2) вида аx + b = 0
и
3) a и b – любый числа.
3 x 12, 5 y 10 0, 2a 7 0,
2
3
z 0
7
5

38.

Составление схемы определения
понятия
Алгебраическая дробь:
1. выражение
2. имеет вид
P
Q
и
и
3. P, Q – многочлены
Определение ближайшего родового понятия.
Выделение видовых отличий.
Структурирование информации.

39.

Составление предписания, выражающего общий
метод решения задач
– выделить тип задач, для которого составляется предписание –
общий метод решения;
– предложить учащимся для решения набор задач, включающий в
себя задачи, соответствующие всем пунктам предписания,
которое составляется;
– организовать решение задач учащимися (оказывая, при
необходимости, помощь);
– обобщить решение задач, устанавливая последовательность
действий, которые были выполнены;
– организовать правильное формулирование выполненных
действий, выстроить последовательность соответствующих
блоков предписания;
– организовать анализ предписания в целом виде.

40.

Составление предписания,
выражающего общий метод решения
Предписание для решения уравнения графически
1. Ввести функции y = x2 и y = bx + c.
2. Построить в одной системе координат графики функций y = x2 и y = bx + c.
3. Найти точки пересечения построенных графиков.
4. Найти абсциссы точек пересечения построенных графиков – это и есть корни заданного
уравнения.
Сравнение.
Построение логической
цепочки рассуждений.
Установление причинноследственных связей.

41.

Составление предписания,
выражающего общий метод решения
Предписание для сложения и вычитания
дробей
1. Сравнить знаменатели.
2. Если все знаменатели одинаковые, то
перейти к пункту 4, если есть разные
знаменатели, то к пункту 3.
3. Привести дроби к общему знаменателю.
4. Выполнить сложение (или вычитание)
числителей, а знаменатель поставить
общий.
5. Выполнить при необходимости
сокращение полученной дроби.

42.

Составление предписания по
решению задач определённого вида
1. Выразим у через х из первого
уравнения системы;
2. Подставим полученное выражение
вместо у во второе уравнение системы;
3. Решим второе уравнение системы;
4. Подставим найденное значение х в
выражение для у.
5. Запишем ответ.

43.

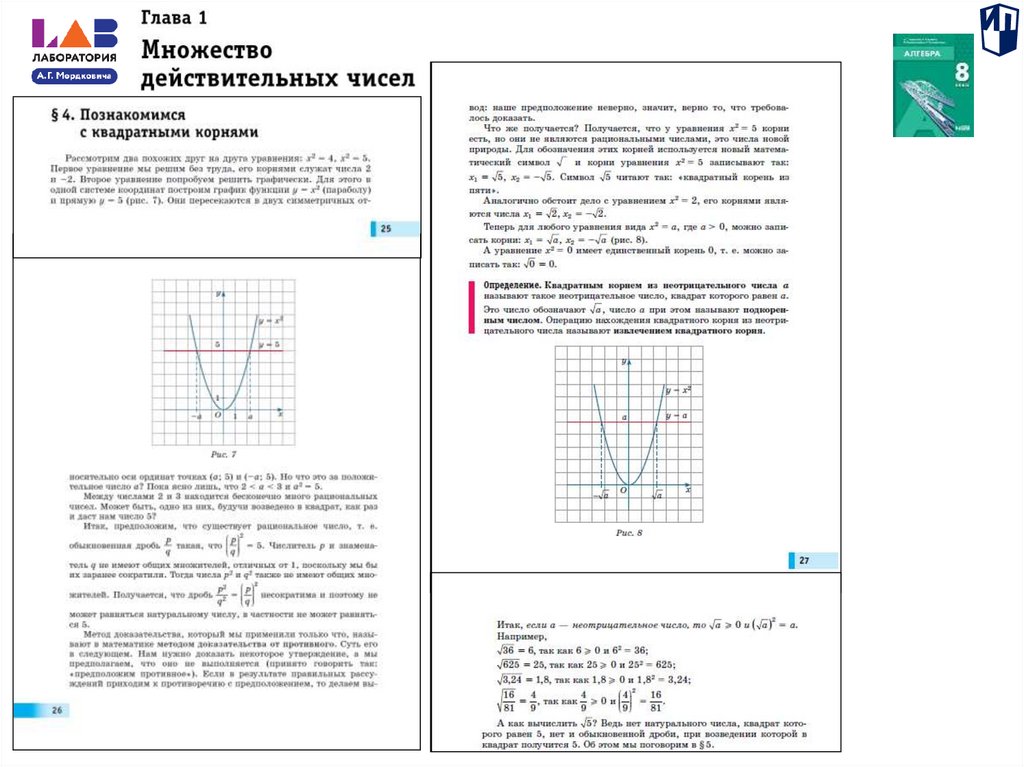
44.

План-схема урока по теме «Познакомимся с квадратными
корнями»
Урок «открытия»
нового знания
Проверка домашнего задания,
актуализация знаний.
Мотивация открытия нового знания.
Побуждение к получению новой
информации.
Получение новой информации
Первичное закрепление с
проговариванием во внешней речи.
Деятельность на уроке
Повторяются: графический способ решения уравнений,
2
построение графика функции y x .
Постановка задачи: решите уравнения
x 2 4 и x 2 5.
Приём «Верю – проверю»
Работа с текстом учебника. Заполнение журнала.
Решение заданий в группах.
Закрепление нового понятия.
Составление схемы определения понятия квадратного
корня.
Составление схемы доказательства.
Самостоятельная работа с самопроверкой Выполнение самостоятельной работы
по эталону.
Рефлексия. Осмысление изученного и
Подведение к выводу: раз мы узнали новый вид числа, то
сделанного
следует его подробно изучить – свойства, расположение
на числовой оси, взаимоотношение с уже известными
рациональными числами.
Информация о домашнем задании,
инструктаж по его выполнению.

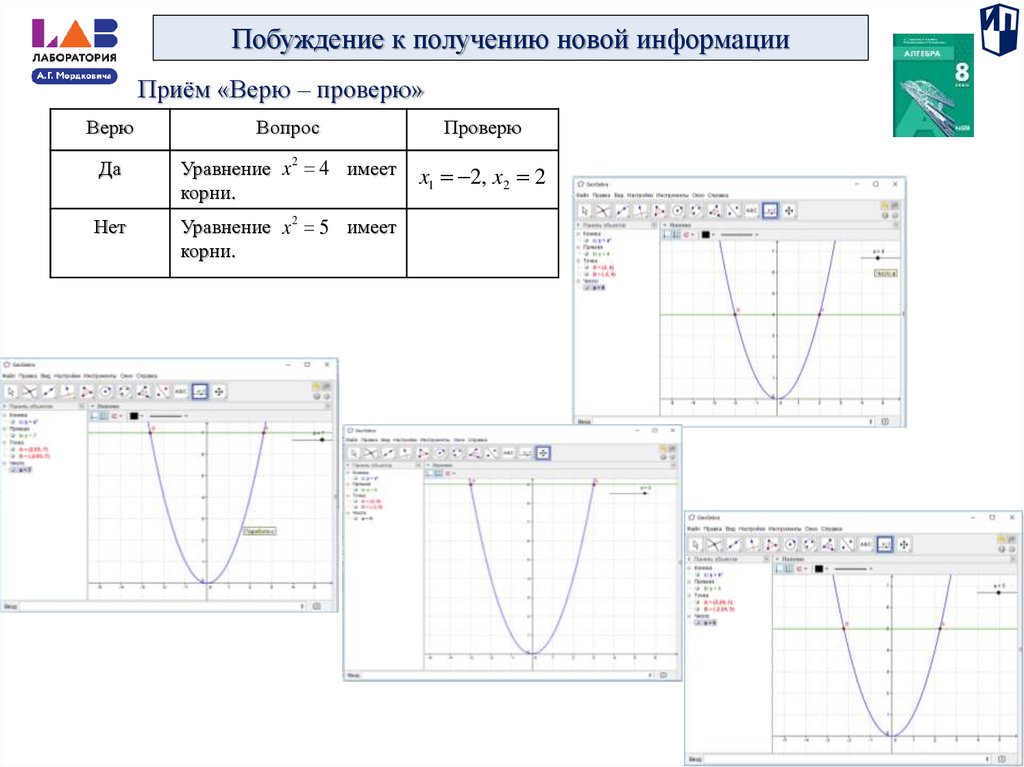
45.

Побуждение к получению новой информации
Приём «Верю – проверю»
Верю
Вопрос
Проверю
Да
Уравнение x 2 4 имеет
корни.
x1 2, x2 2
Нет
Уравнение x 2 5 имеет
корни.

46.

Получение новой информации
Составление схемы
определения понятия
2
p
– рациональное число; 5.
q
1.
p
Пусть
q
2.
p, q
не имеют общих делителей.
3.
p2 , q2
не имеют общих делителей.
p2 p
4. 2
q
q
2
несократима. Противоречие с п.1.

47.

Получение новой информации
Составление схемы
определения понятия
Корень квадратный из неотрицательного числа а:
1) Неотрицательное число
2) Квадрат этого числа равен а.
Показатель корня
(2 не пишется)
a 0,
2
и
Квадратный корень из
неотрицательного числа а
Подкоренное
выражение
a
a
2
a, a 0

48.

Лист рефлексии
Основная деятельность учащегося
Повторение: графический способ решения уравнений,
построение графика функции.
Постановка задачи: решите уравнения.
Работа с текстом учебника. Заполнение журнала.
Анализ и формулировка проблемы. Выдвижение гипотезы:
существует рациональное число, квадрат которого равен 5.
Проверка гипотезы.
Получение результата: понятие квадратного корня.
Выполнение самостоятельной работы.
Работа с текстом учебника. Получение образовательного
продукта: схемы доказательства иррациональности числа.
Решение заданий в группах.
Закрепление нового понятия.
Составление схемы определения понятия квадратного корня.
Подведение к выводу: раз мы узнали новое понятие, то следует
более подробно изучить его свойства, взаимоотношение с уже
известными понятиями.
Справился
сам
Справился
с помощью
Не
справился

49.

Рефлексия учебной деятельности
• Удалось ли мне решить поставленные перед собой на уроке задачи?
• Достигнута ли мною цель урока?
• Что мне удалось на уроке?
• Что я для этого сделал(а) (обсуждение результатов заполнения листа
рефлексии)?
• Что у меня не получилось на уроке?
• Что мне помешало?
• Что я должен сделать, чтобы в следующий раз получилось?
• Какую оценку я заслужил в соответствии с критериями?
• Определение домашнего задания и ближайших задач.

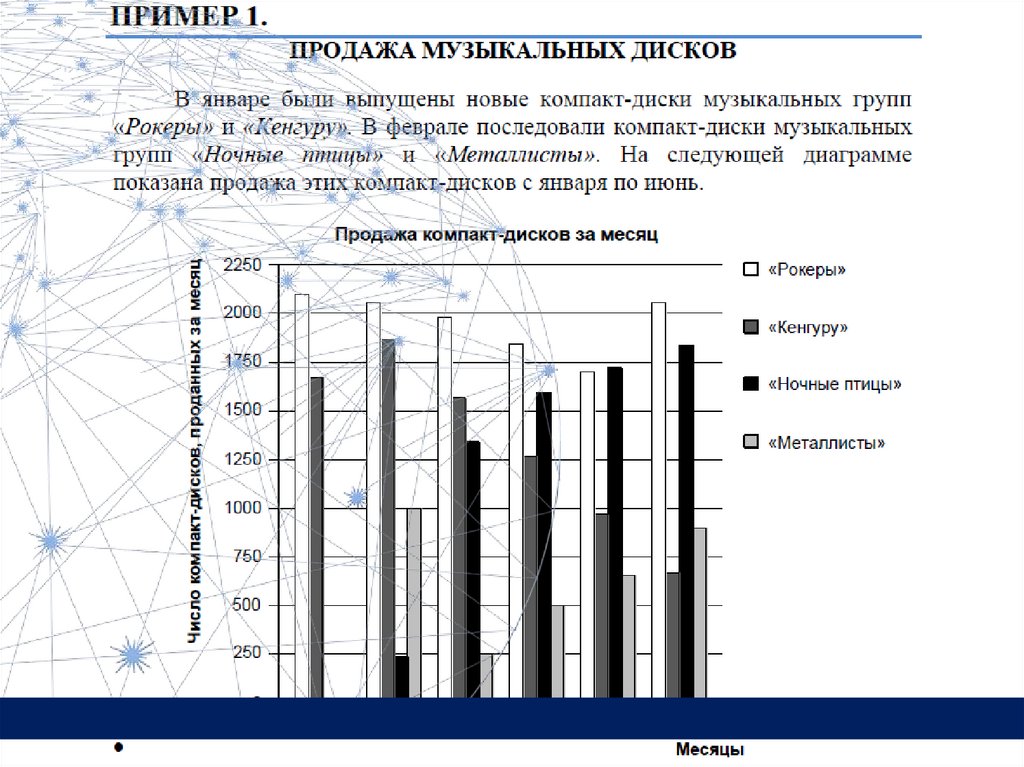
50.

Пример 1.
31 декабря 2014 года Дмитрий взял в банке 4290000 рублей в кредит под 14,5%
годовых. Схема выплаты кредита следующая – 31 декабря каждого
следующего года банк начисляет проценты на оставшуюся сумму долга (то
есть увеличивает долг на 14,5%), затем Дмитрий переводит в банк Х рублей.
Какой должна быть сумма Х, чтобы Дмитрий выплатил долг двумя равными
платежами (то есть за два года)?
Решение: Пусть сумма кредита равна S, а годовые составляют а%.
Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент
равный р = 1 + 0,01а.
После первой выплаты сумма долга составит
После второй выплаты сумма долга составит
По условию двумя выплатами Дмитрий должен погасить кредит полностью, поэтому
Откуда при S = 4290000 и а = 14,5, получаем: р = 1,145 и
Ответ: 2622050.

51.

Пример 2.
31 декабря 2014 года Алексей взял в банке 6902000 рублей в кредит под 12,5% годовых.
Схема выплаты кредита следующая – 31 декабря каждого следующего года банк начисляет
проценты на оставшуюся сумму долга (то есть увеличивает долг на 12,5%), затем Алексей
переводит в банк Х рублей. Какой должна быть сумма Х, чтобы Алексей выплатил долг
четырьмя равными платежами (то есть за четыре года)?
Решение. Пусть сумма кредита равна S, а годовые составляют а %.
Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент
р = 1 + 0,01a. После первой выплаты сумма долга составит
После второй выплаты сумма долга составит
После третьей выплаты сумма оставшегося долга равна
После четвертой выплаты сумма оставшегося долга равна
По условию четырьмя выплатами Алексей должен погасить кредит полностью, поэтому
Откуда при S = 6902000 и а = 12,5, получаем: р = 1,125 и
Ответ: 2296350
.

52.

Пример 3.
31 декабря 2014 года Георгий взял в банке кредит размером 1 млн рублей. Схема
выплаты кредита следующая – 31 декабря каждого года банк начисляет проценты
на оставшуюся сумму долга (то есть увеличивает долг на а%), затем Георгий
переводит очередной транш. Георгий выплатил кредит за два транша, переведя в
первый раз 570 тыс. рублей, во второй 599,4 тыс. рублей. Под какой процент банк
выдал кредит Георгию?
Решение. Пусть сумма кредита равна S, а годовые составляют а %. Тогда 31 декабря
каждого года оставшаяся сумма долга умножается на коэффициент р = 1 + 0,01a.
После первой выплаты сумма долга составит
Исходя из условия после первой выплаты долг Георгия будет равен
После второй выплаты сумма долга составит S2 = (430000 + 10000а) р – 599 400
При условии, что кредит был погашен за два транша это сумма должна равняться 0.
После преобразований получим уравнение
Отсюда а1 = –154; а2 = 11.
Ответ: 11%.
.

53.

УМК «Лаборатория А.Г. Мордковича»
Алгебра 7-9 классы. Алгебра и начала математического анализа 10-11 классы

54.

профессор МГПУ, доктор педагогических наук, кандидат физико-математических наук,
научный руководитель Международного семинара преподавателей математики педвузов
(1987 г-н.в.);
имеет награды: Премия Президента РФ в области образования, заслуженный деятель науки
РФ, Отличник народного образования, Медаль К.Д.Ушинского.
профессор факультета математики НИУ ВШЭ, доктор физико-математических наук,
профессор, член Федеральной предметной группы по разработке КИМ для ЕГЭ по математике
(2001-2007 гг), разработчик заданий с развернутым ответом, автор более 20 учебнометодических пособий по подготовке учащихся к ЕГЭ и подготовке экспертов к проверке
работ учащихся;
имеет награды: Почётный работник высшего профессионального образования РФ; Почетная
грамота Министерства образования РФ.
учитель математики, методист ГБОУ Школы 1317 г. Москва, учитель высшей категории, член
предметной комиссии по проверке выполнения заданий с развернутым ответом экзаменационных
работ ЕГЭ по математике;
имеет награды: Отличник народного просвещения РФ.
заведующий лабораторией математики службы продвижения «Бином», кандидат педагогических
наук, доцент, председатель предметной комиссии ЕГЭ по математике Московской области (20062007 гг); член-корреспондент Международной академии научного педагогического образования
(МАНПО);
имеет награды: Грант Москвы в сфере образования; Почётная грамота Министерства образования
Московской области.

55.

Алгебра, 7-9-е классы
Алгебра и начала математического анализа, 10-11
классы
Включены в Федеральный перечень
Учебники
ЭФУ
Примерные рабочие программы
Методические пособия для учителя
Рабочие тетради
Контрольные работы
Самостоятельные и проверочные работы
Алгебраические практикумы

56.

Отличительные особенности
УМК «Лаборатория А.Г. Мордковича»
Курс построен на основе приоритетности функционально-графической
линии, математическое моделирование является идейным стержнем.
Учебник и задачник соединены в одну книгу.
Порядок тем соответствует ПООП, отражает психологические
особенности обучающихся.
Выстроена вероятностно-стохастическая линия в тесной взаимосвязи с
основным содержанием.
Каждая глава содержит разделы «Повторение», «Итак, в Главе…»,
«Вопросы», «Дополнительные задачи», «Из истории математики».
Трёхуровневая система заданий отражает требования ФГОС ОО,
итоговой аттестации. Добавлены задачи практического содержания,
высокого уровня сложности.
Включён материал, рекомендованный к изучению с использованием ITсредств.

57.

Математика, 5-6 классы
Авторы: Н.Б.Истомина,
О.П.Горина, Н.Б.Тихонова
Включены в Федеральный перечень
Учебники
Рабочие тетради
Тестовые задания
Методические пособия для учителя
Пособия для внеурочной деятельности:
«Наглядная геометрия», «Учимся решать
комбинаторные задачи»

58.

Авторский сайт https://elenamard.jimdo.com

59.

Методическая поддержка через сайт издательства http://www.lbz.ru

60.

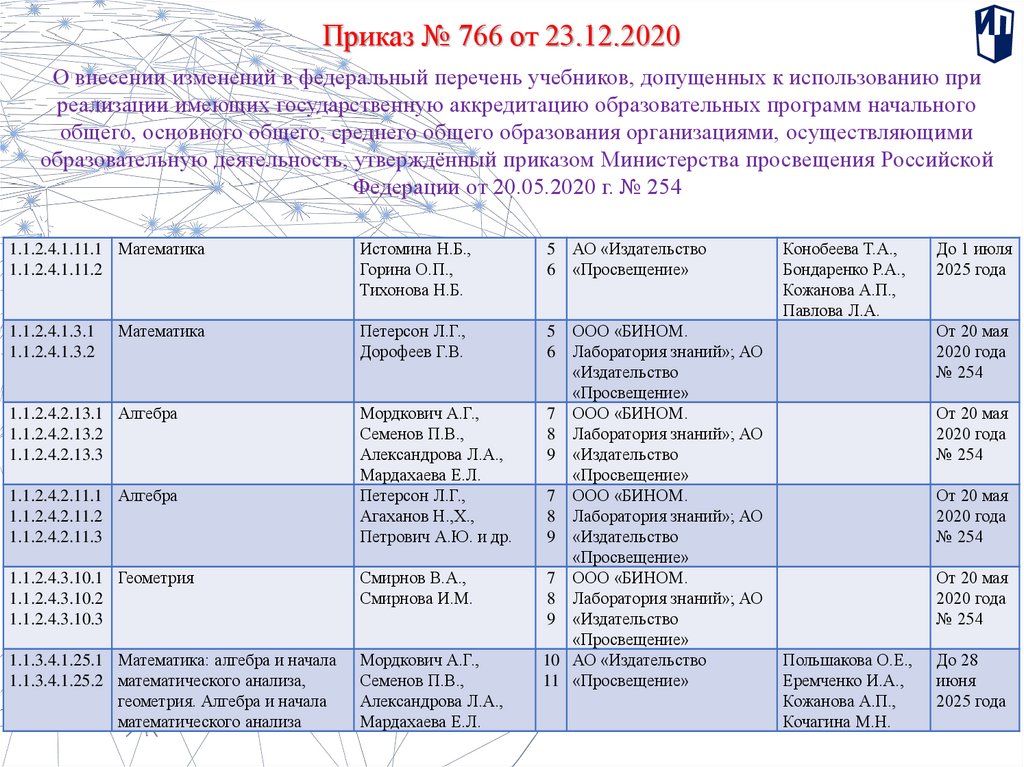
Приказ № 766 от 23.12.2020
О внесении изменений в федеральный перечень учебников, допущенных к использованию при
реализации имеющих государственную аккредитацию образовательных программ начального
общего, основного общего, среднего общего образования организациями, осуществляющими
образовательную деятельность, утверждённый приказом Министерства просвещения Российской
Федерации от 20.05.2020 г. № 254
1.1.2.4.1.11.1 Математика
1.1.2.4.1.11.2
1.1.2.4.1.3.1
1.1.2.4.1.3.2
Математика
1.1.2.4.2.13.1 Алгебра
1.1.2.4.2.13.2
1.1.2.4.2.13.3
1.1.2.4.2.11.1 Алгебра
1.1.2.4.2.11.2
1.1.2.4.2.11.3
Истомина Н.Б.,
Горина О.П.,
Тихонова Н.Б.
5 АО «Издательство
6 «Просвещение»
Петерсон Л.Г.,
Дорофеев Г.В.
5 ООО «БИНОМ.
6 Лаборатория знаний»; АО
«Издательство
«Просвещение»
7 ООО «БИНОМ.
8 Лаборатория знаний»; АО
9 «Издательство
«Просвещение»
7 ООО «БИНОМ.
8 Лаборатория знаний»; АО
9 «Издательство
«Просвещение»
7 ООО «БИНОМ.
8 Лаборатория знаний»; АО
9 «Издательство
«Просвещение»
10 АО «Издательство
11 «Просвещение»
Мордкович А.Г.,
Семенов П.В.,
Александрова Л.А.,
Мардахаева Е.Л.
Петерсон Л.Г.,
Агаханов Н.,Х.,
Петрович А.Ю. и др.
1.1.2.4.3.10.1 Геометрия
1.1.2.4.3.10.2
1.1.2.4.3.10.3
Смирнов В.А.,
Смирнова И.М.
1.1.3.4.1.25.1 Математика: алгебра и начала
1.1.3.4.1.25.2 математического анализа,
геометрия. Алгебра и начала
математического анализа
Мордкович А.Г.,
Семенов П.В.,
Александрова Л.А.,
Мардахаева Е.Л.
Конобеева Т.А.,
Бондаренко Р.А.,
Кожанова А.П.,
Павлова Л.А.
До 1 июля
2025 года
От 20 мая
2020 года
№ 254
От 20 мая
2020 года
№ 254
От 20 мая
2020 года
№ 254
От 20 мая
2020 года
№ 254
Польшакова О.Е.,
Еремченко И.А.,
Кожанова А.П.,
Кочагина М.Н.
До 28
июня
2025 года

61.

Спасибо за внимание!
Удачи в делах!
Адрес обратной связи:
[email protected]
Авторский сайт:
https://elenamard.jimdo.com/
Сайт издательства:
http://lbz.ru/
Мы готовы с диалогу!