Similar presentations:
Диференціальні рівняння. Загальні визначення (лекція 4)
1.
ДИФЕРЕНЦІАЛЬНІРІВНЯННЯ
Лекція 4
2.
Загальні визначенняДиференціальним рівнянням називають співвідношення, що позв'язує
між собою незалежну змінну, функцію та її похідні (чи диференціали)
•Порядком диференціального рівняння називають найбільший порядок похідної
(чи диференціала), що входить у рівняння.
•У загальному виді диференціальне рівняння п-го порядку може бути записано
таким чином:
F ( x, y, y , y ,..., y ( n ) ) 0
(1)
У цьому рівнянні x – незалежна змінна, y - невідома функція,
y/, y//, y(n) - похідні функції.
•Звичайне диференціальне рівняння першого порядку можна записати у
такому вигляді:
F ( x, y, y ) 0
(2)
3.
•Загальним розв’язком диференціального рівняння п-го порядку називаєтьсяфункція:
(3)
y f ( x, C1 , C2 ,..., Cn )
де
- сталі величини.
C1 , C2 ,..., C n
Загальним розв’язком диференціального рівняння першого порядку
називається функція:
y f ( x, C )
(4)
•Частинним розв’язком диференціального рівняння (2) називають такий розв’язок,
що можна одержати із загального розв’язку (4) при деякому конкретному значенні
сталої величини С. Це значення знаходять при, так званих, початкових умовах :
y y0
розв’язавши рівняння
x x0 ,
y 0 f ( x0 , C )
відносно С.
4.
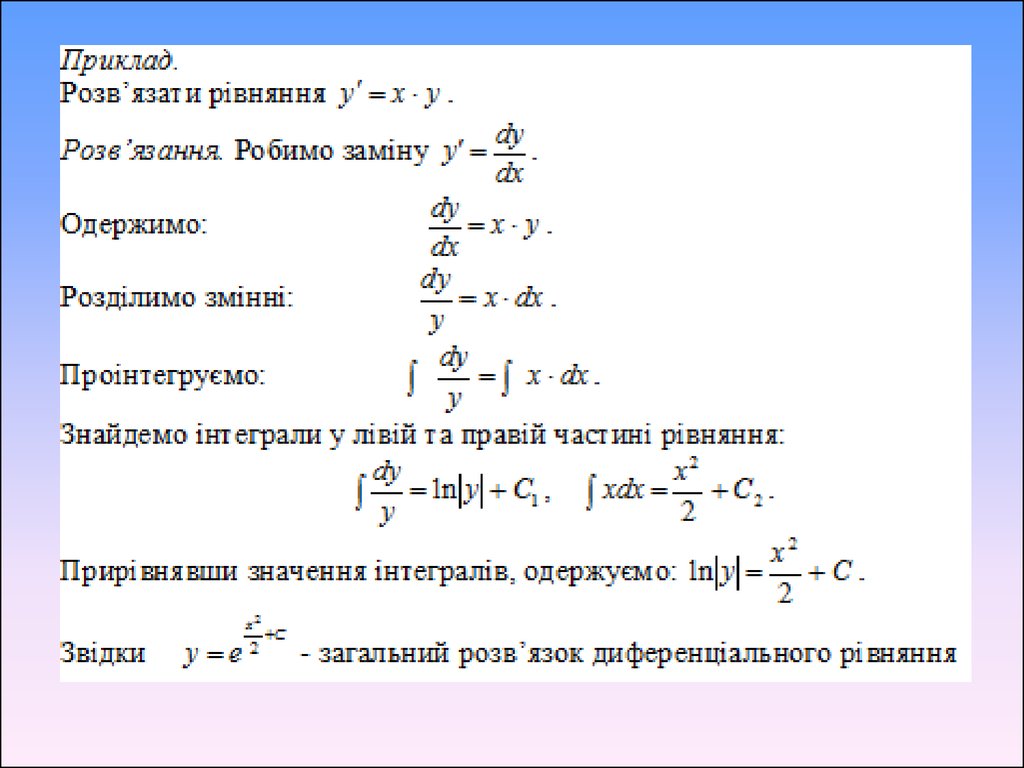
Рівняння з відокремлюваними змінними5.
6.
7. Однорідні диференціальні рівняння першого порядку
8.
9. Диференціальні рівняння другого порядку
10. Рішення окремих випадків диференціальних рівнянь другого порядку.
11.
12.
Рішення окремих випадків диференціальних рівняньдругого порядку.















 mathematics
mathematics








