Similar presentations:
Ряды. Введение в математический анализ
1.
РядыВведение в математический анализ
2.
План вебинара1) Разбор ДЗ.
2) Ряды.
2.1) Сходимость (знакоположительные;
знакопеременные ряды).
2.2) Ряды Тейлора и Маклорена.
2.3) Ряд Фурье.
2
3.
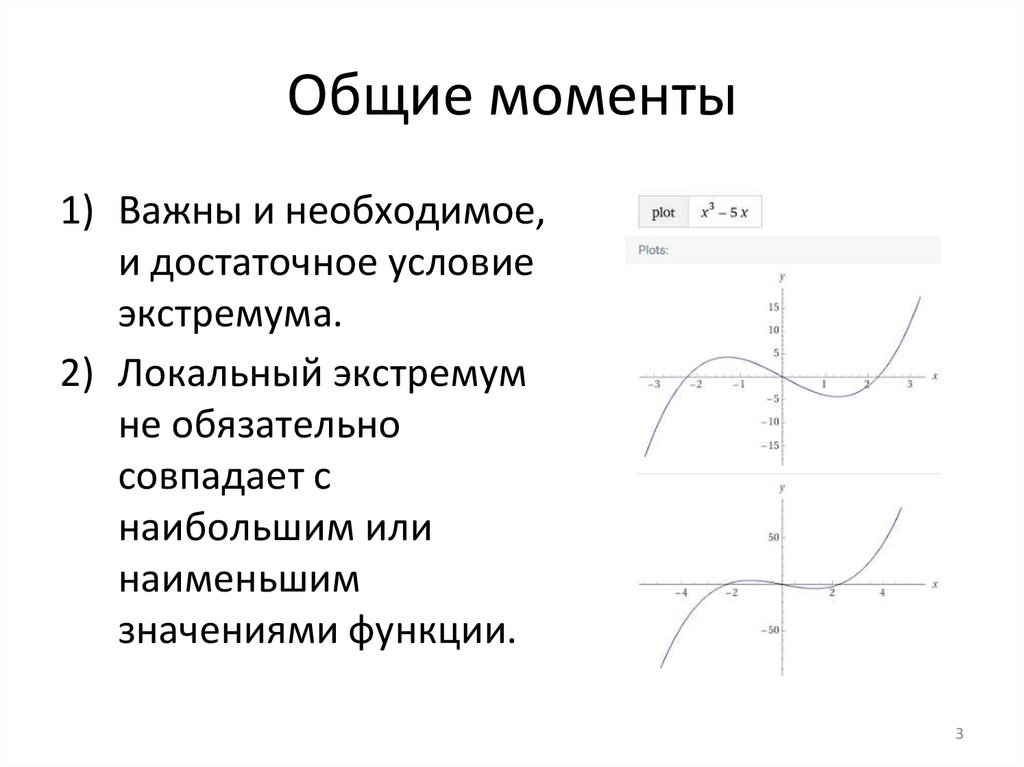
Общие моменты1) Важны и необходимое,
и достаточное условие
экстремума.
2) Локальный экстремум
не обязательно
совпадает с
наибольшим или
наименьшим
значениями функции.
3
4.
Разбор ДЗ (ФНП). Часть 2.4
5.
56.
МинимумМаксимум
Иллюстрация
задачи на
максимум:
https://www.wolf
ramalpha.com/inp
ut/?i=maximize+3
8x%2B6y+on+x%5
E2%2By%5E2%3D
36
6
7.
78.
89.
МаксимумМинимум
Минимум
Максимум
9
10.
Графики• Задача максимизации:
https://www.wolframalpha.com/input/?i=maxi
mize+2x%5E2%2B12xy%2B32y%5E2%2B15+on+
x%5E2%2B16y%5E2%3D64
• Задача минимизации:
https://www.wolframalpha.com/input/?i=mini
mize+2x%5E2%2B12xy%2B32y%5E2%2B15+on+
x%5E2%2B16y%5E2%3D64
10
11.
1112.
1213.
1314.
1415.
1516.
1617.
Ряды17
18.
Числовой ряд – это бесконечнаясумма
18
19.
Сходимость рядаЕсли ряд сходится, мы можем найти сумму
ряда.
Т.е. сумма не растет до бесконечности, а
складывается в определенное число.
19
20.
Зачем нужны рядыСпособ исследовать и аппроксимировать
функцию (приблизительно описать).
20
21.
2122.
Знакочередующийся22
23.
Если необходимое условие выполняется,то ряд может сходиться и нужны дополнительные исследования (достаточное
условие).
Если необходимое условие не выполняется, то ряд точно не сходится.
Необходимые условия нужны, чтобы отсеять наверняка не сходящиеся ряды.
Но окончательный положительный ответ про сходимость по необходимому
условию мы дать не можем.
23
24.
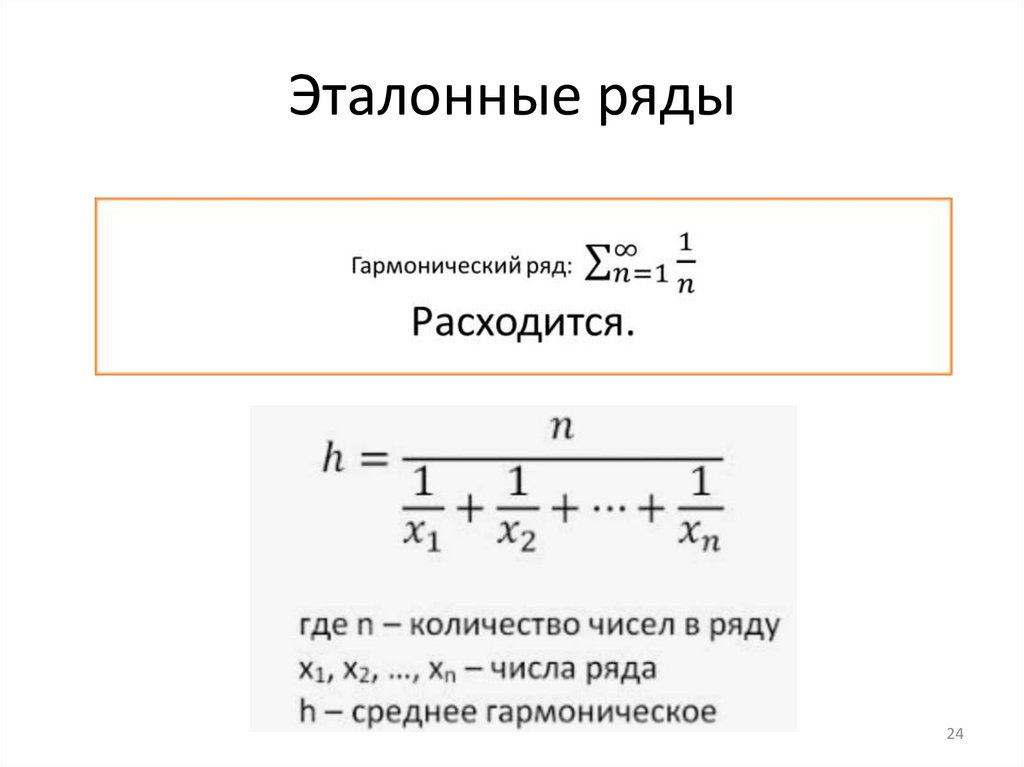
Эталонные ряды24
25.
Эталонные ряды25
26.
Эталонные ряды26
27.
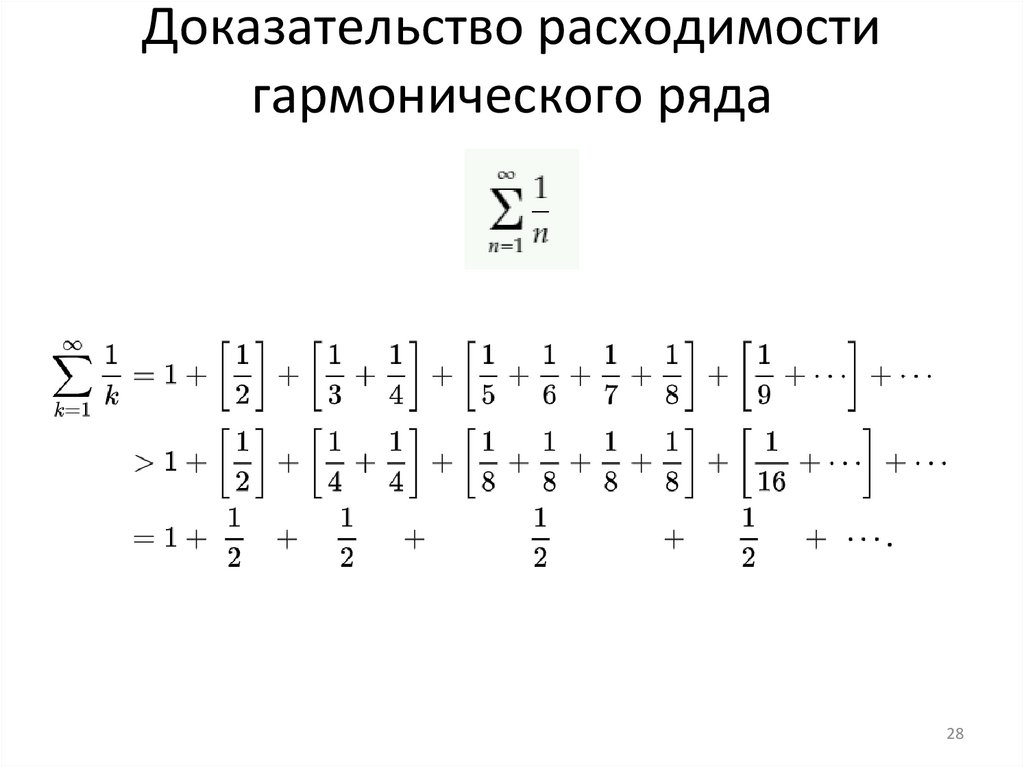
Доказательство расходимостигармонического ряда
27
28.
Доказательство расходимостигармонического ряда
28
29.
Признак=необходимое условие + достаточноеусловие
29
30.
3031.
2-й признак сравнения(предельный)
31
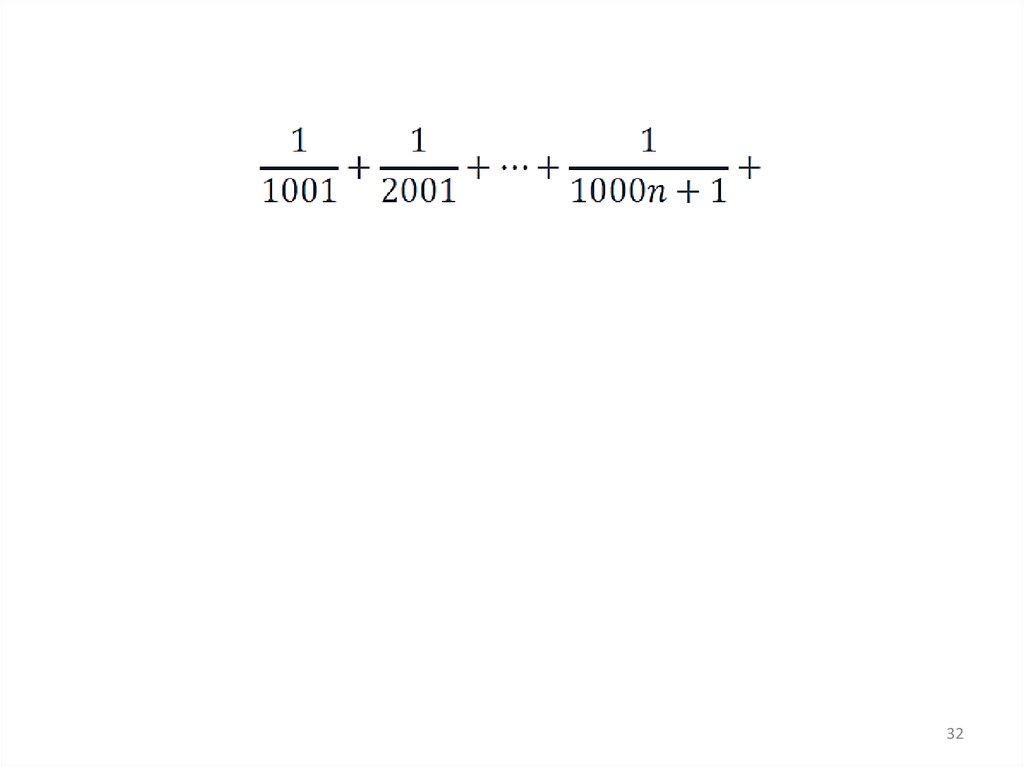
32.
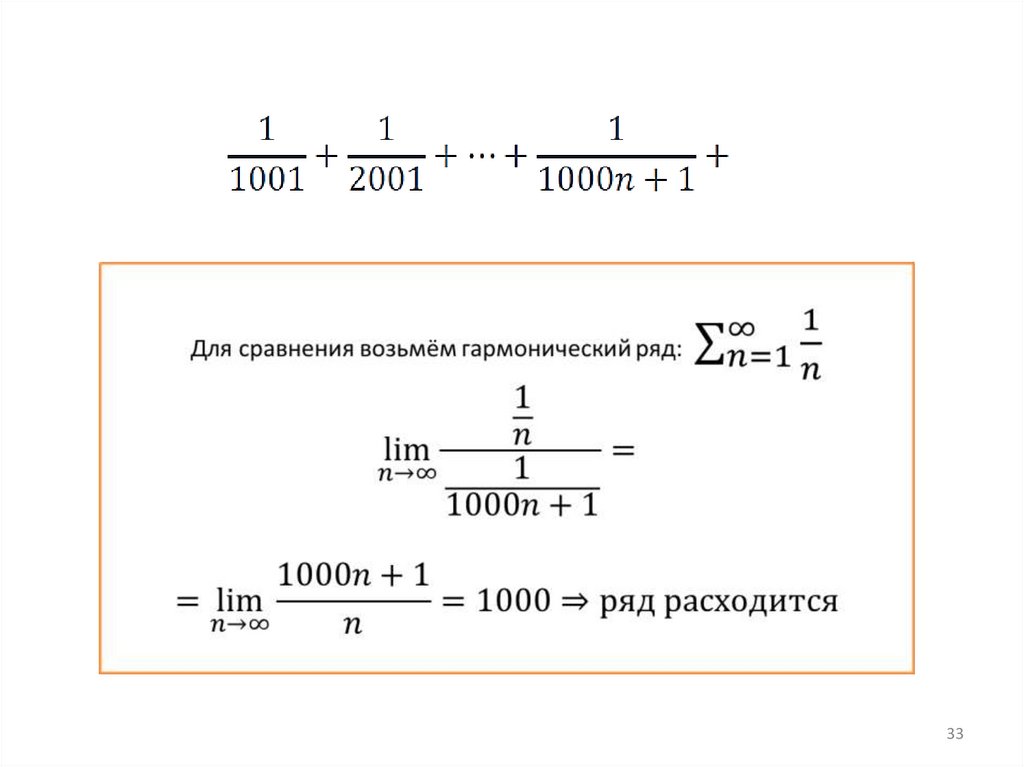
3233.
3334.
3435.
3536.
Сильный признак, но не всесильный:q=1 => нужны дополнительные исследования.
36
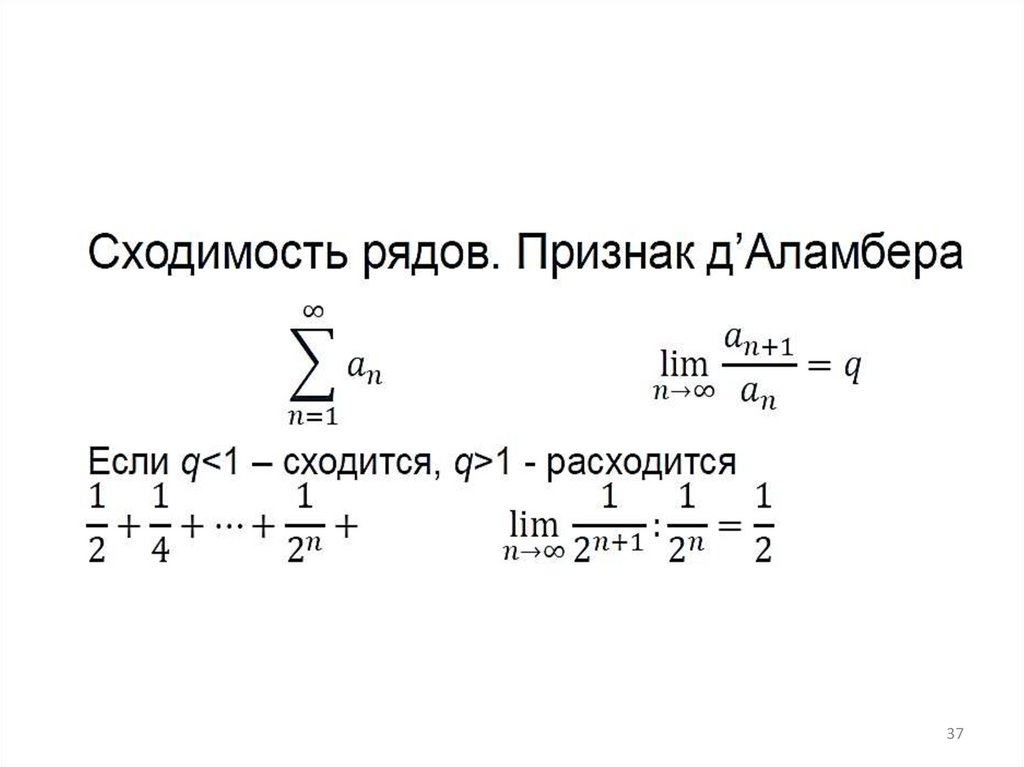
37.
3738.
Самый популярный признак, нопри q=1 нужны дополнительные
исследования.
38
39.
Ряд сходитсяРяд сходится
39
40.
Радикальный признак Коши40
41.
Радикальный признак Коши.Пример.
41
42.
Радикальный признак Коши.Пример.
0<1 -> ряд сходится
42
43.
Признак РаабеИсточник: http://mathprofi.ru/slozhnye_ryady.html
43
44.
Признак Раабе – пример.44
45.
Несобственные интегралы.Дополнение.
Дан несобственный интеграл:
45
46.
Интегральный признак КошиДанный ряд сходится одновременно с
несобственным интегралом:
То есть, если такой интеграл можно посчитать, и он не
равен бесконечности, ряд сходится.
46
47.
Исследовать ряд с помощьюинтегрального признака Коши
Для этого нужно посчитать
интеграл:
47
48.
Исследовать ряд с помощьюинтегрального признака Коши
Для этого нужно посчитать
интеграл:
48
49.
Исследовать ряд с помощьюинтегрального признака Коши
Для этого нужно посчитать
интеграл:
!замена пределов интегрирования при замене
переменной!
49
50.
Интеграл расходится,следовательно
расходится и ряд.
50
51.
Давайте исследуем и этот ряд51
52.
Для этого найдём интеграл52
53.
Для этого найдём интеграл!замена пределов интегрирования при замене
переменной!
53
54.
Интегралсходится,
следовательно
ряд тоже
сходится.
54
55.
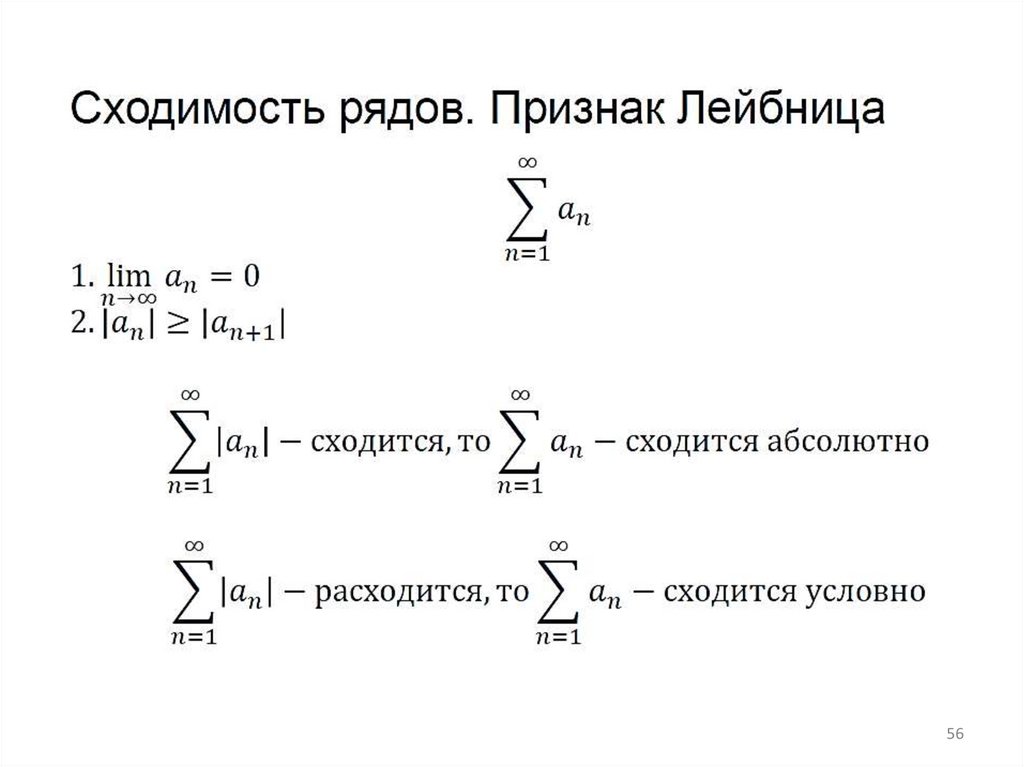
Сходимость рядов:знакочередующиеся ряды
55
56.
5657.
5758.
=58
59.
=Используются для аппроксимации функции многочленами
59
60.
6061.
6162.
6263.
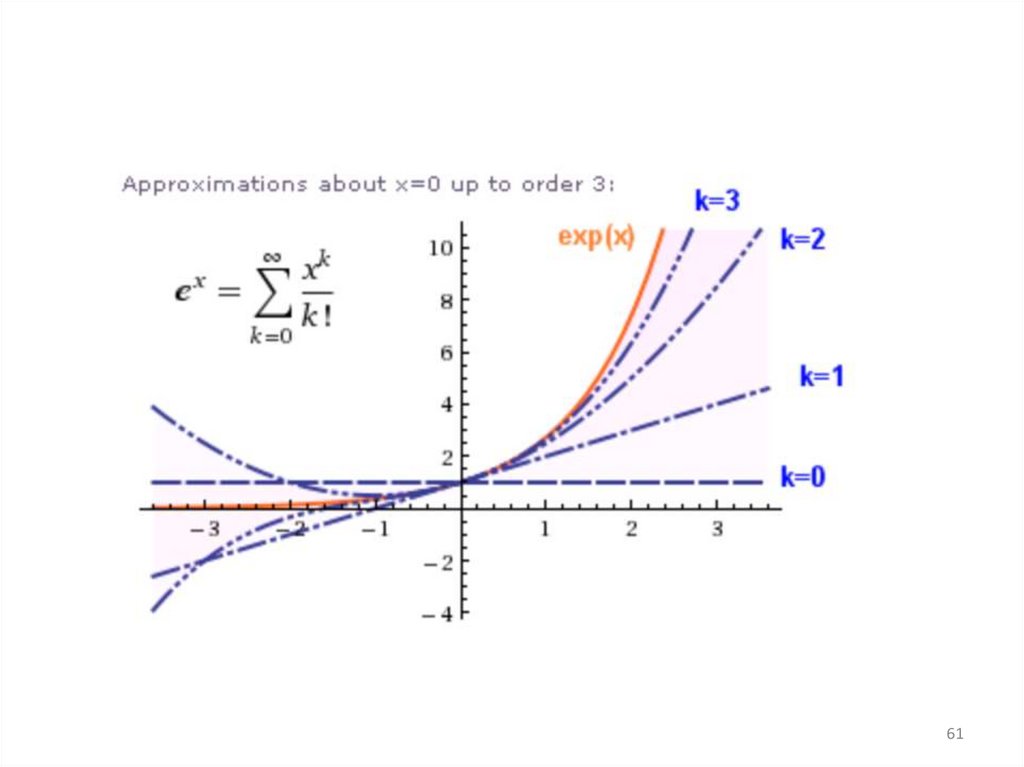
Ряд Маклорена (ряд Тейлора вокрестности точки 0)
63
64.
6465.
6566.
6667.
6768.
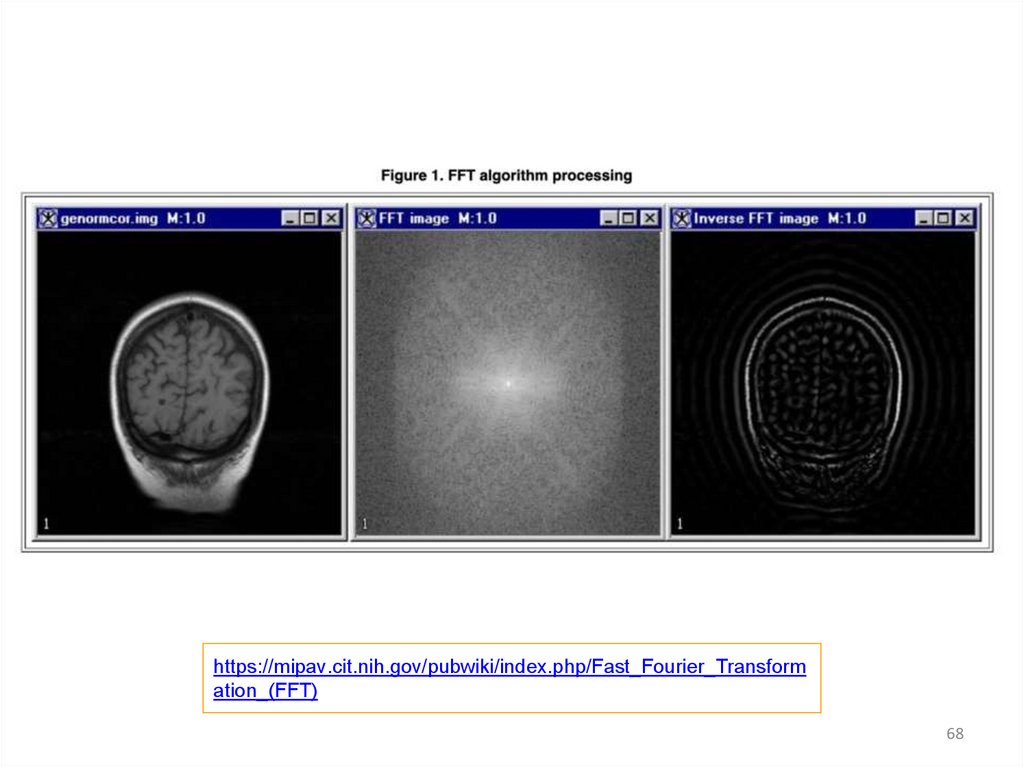
https://mipav.cit.nih.gov/pubwiki/index.php/Fast_Fourier_Transformation_(FFT)
68
69.
Fast Fourier transformation (FFT).Применяются в аудио формате .mp3.
До этого формата аудио дорожка хранилась в
виде массива времени и значения амплитуды
звуковой волны.
В формате .mp3 хранятся уже коэффициенты FFT.
При этом существо сокращается место на
хранение звуковой дорожки. Все современные
мультимедийные
форматы,
особенно
работающие в Интернете, как правило,
построены на FFT.
69
70.
Спасибо!Успехов!





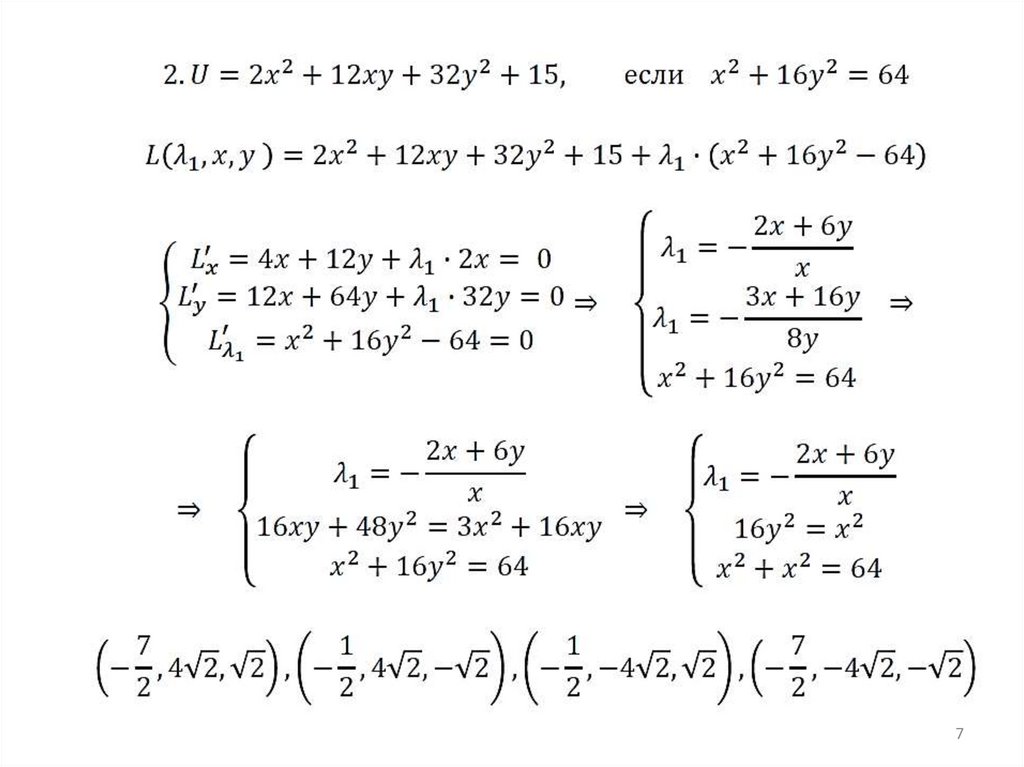





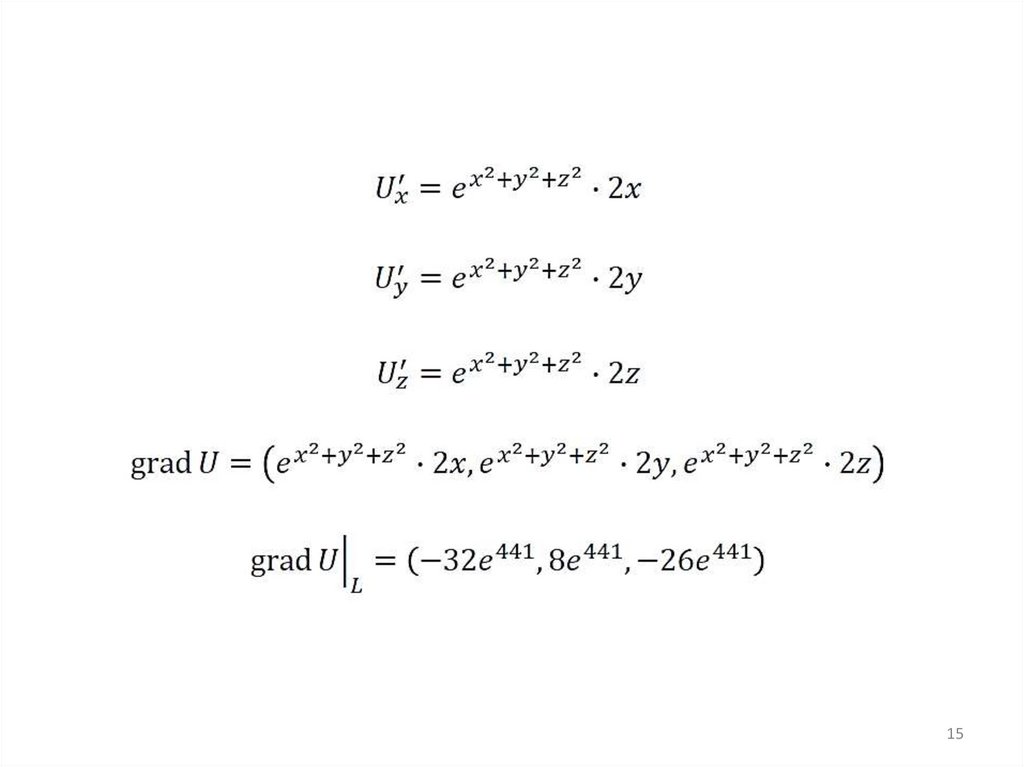
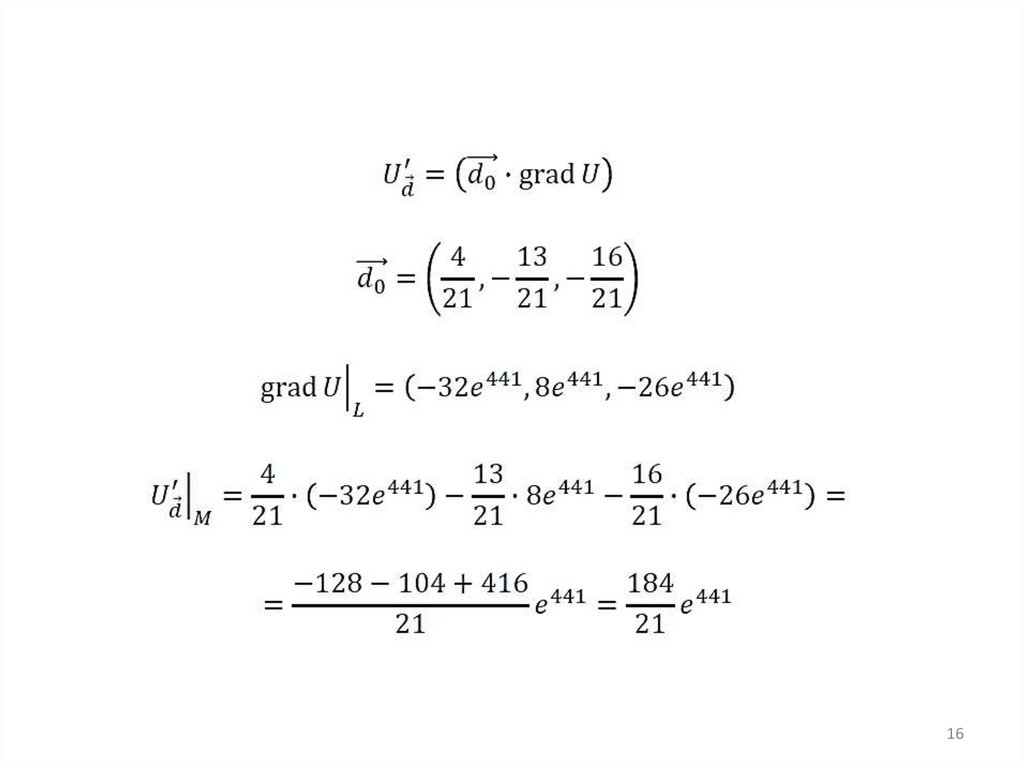













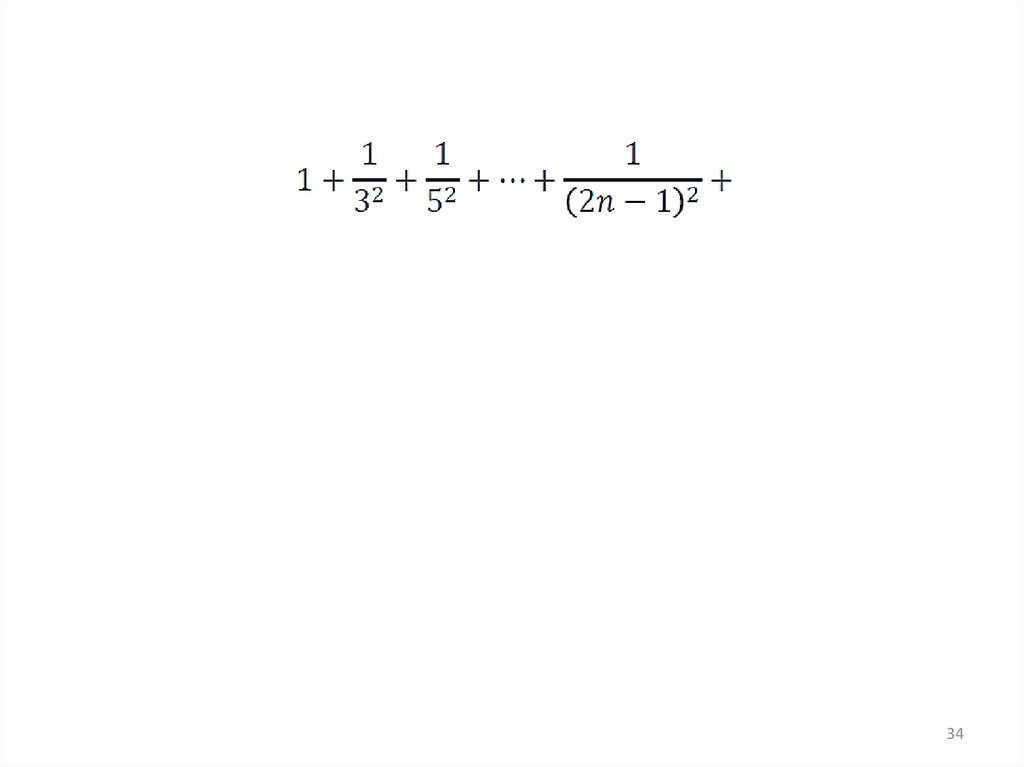
































 mathematics
mathematics








