Similar presentations:
Интегралы. Введение в математический анализ
1.
ИнтегралыВведение в математический анализ
2.
План вебинара1)Разбор ДЗ
2) Интегралы:
- неопределённые интегралы
- определённые интегралы
3) Дифференциальные уравнения
2
3.
Разбор ДЗ (ФНП). Часть 1.1.
Найти область определения функции.
3
4.
2.Найти частные производные 1-го
порядка функции.
4
5.
56.
3.Найти полный дифференциал функции
в точке (1;1).
6
7.
78.
89.
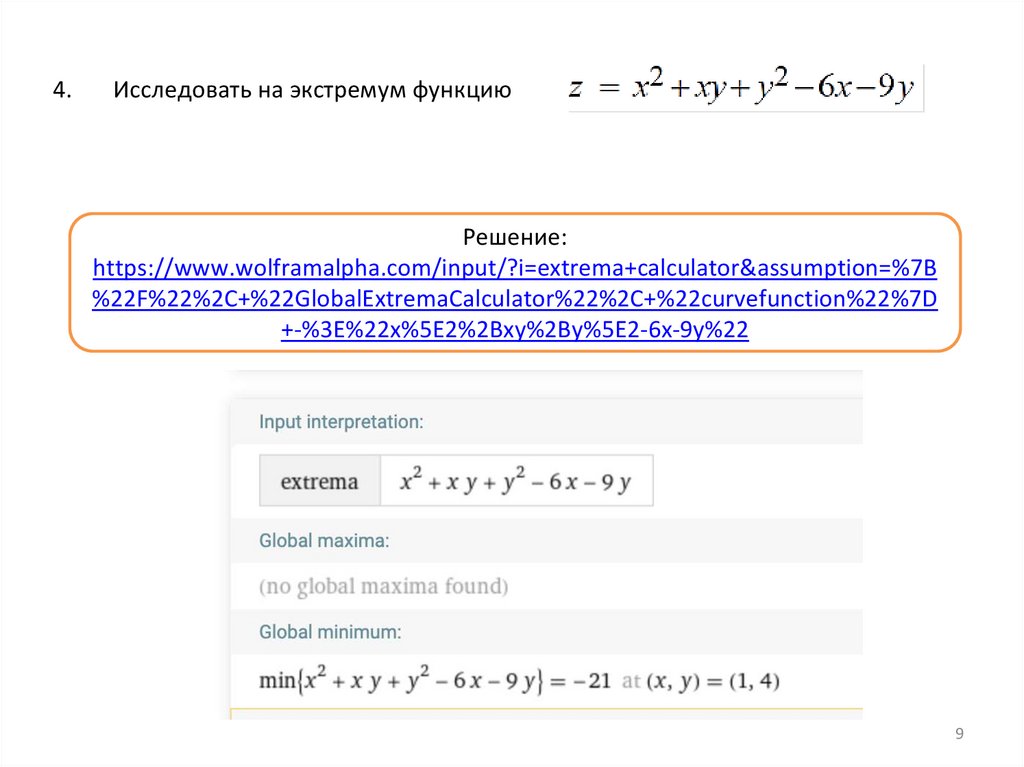
4.Исследовать на экстремум функцию
Решение:
https://www.wolframalpha.com/input/?i=extrema+calculator&assumption=%7B
%22F%22%2C+%22GlobalExtremaCalculator%22%2C+%22curvefunction%22%7D
+-%3E%22x%5E2%2Bxy%2By%5E2-6x-9y%22
9
10.
1011.
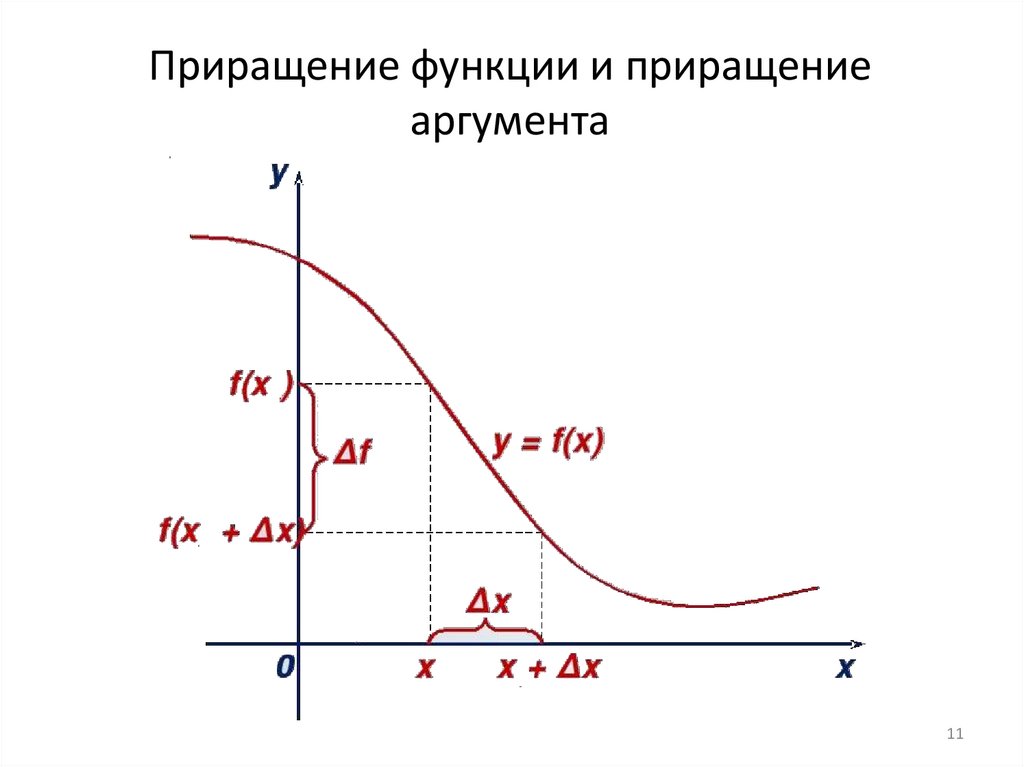
Приращение функции и приращениеаргумента
11
12.
1213.
1314.
Интегрированиепо сути, это противодействие
дифференцированию.
Знак интегрирования:
SQUARE -> S ->
14
15.
При интегрировании проверить себя довольно просто: достаточно взятьпроизводную от ответа - должна получится функция под интегралом.
15
16.
1617.
Основные правила интегрирования17
18.
1819.
1920.
Весь процесс интегрирования сводится к тому,что необходимо привести подынтегральную
функцию к табличному виду.
20
21.
2122.
2223.
Метод замены переменной(по сути, он идентичен внесению под знак
дифференциала)
23
24.
В этом методе важно вернуться к исходной переменной:24
25.
2526.
Источник:26
27.
Интегрируем правую и левую части27
28.
2829.
2930.
3031.
Какие интегралы берутся по частям31
32.
Дробь правильная(старшая степень выражения в знаменателе
выше степени выражения в числителе)
32
33.
3334.
3435.
3536.
3637.
3738.
3839.
3940.
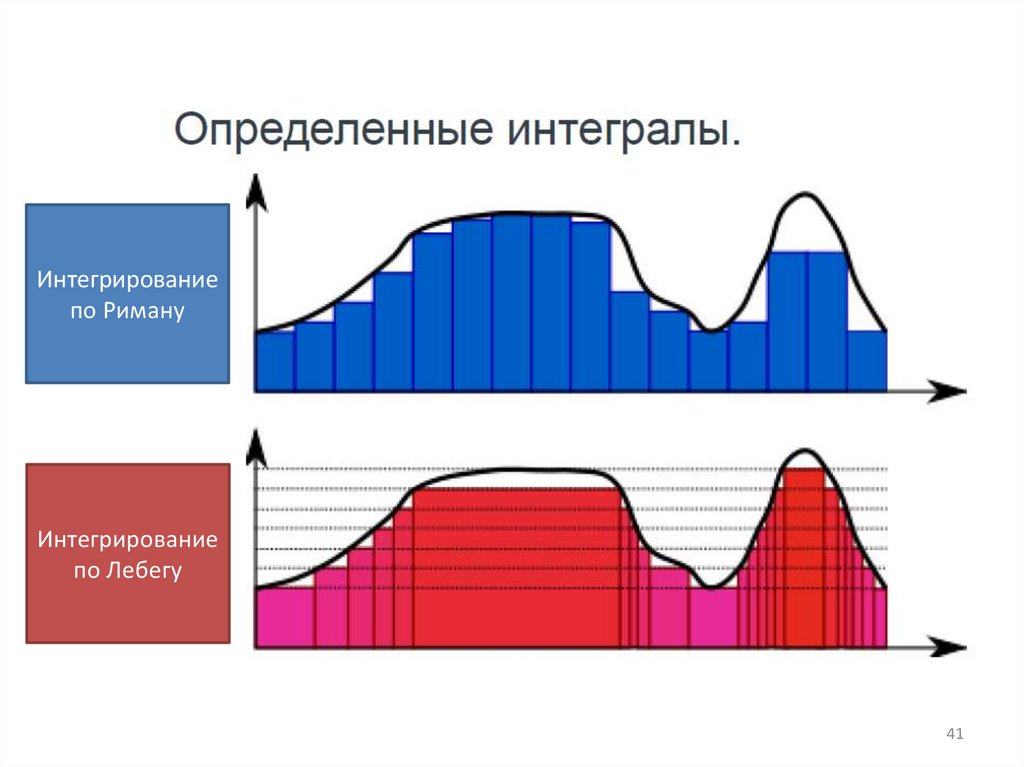
Для интеграла Римана функция должна быть непрерывна идифференцируема во всех точках заданного отрезка [a,b] . Для
интеграла Лебега таких ограничений нет.
Т.е. интеграл Лебега совпадает с интегралом Римана там, где интеграл
Римана существует. При этом интеграл Лебега можно брать и от не
дифференцируемых в точке функций. Например, от функции Дирихле.
40
41.
Интегрированиепо Риману
Интегрирование
по Лебегу
41
42.
Статьи по интегралам Лебега• Интеграл Лебега:
https://mathworld.wolfram.com/LebesgueInt
egral.html
• Мера Лебега:
https://mathworld.wolfram.com/Measure.html
• Пример вычисления интеграла Лебега:
https://demonstrations.wolfram.com/LebesgueI
ntegration/
42
43.
4344.
4445.
4546.
4647.
4748.
4849.
4950.
Несобственные интегралыопределённые интегралы с особенностями
на границах.
Одна из границ - бесконечность
Особенность на
одной из границ
интегрирования
50
51.
Примеры вычислениянесобственных интегралов
51
52.
Дифференциальные уравнения: гдеприменяются.
DSP (Цифровая обработка сигналов)
Computer vision
«Анализ любых экспериментальных данных (зависимости величин) - только
диффуры! А это - весь мир». (c, @xmoonlight, https://qna.habr.com/q/149841)
52
53.
Решение дифференциальныхуравнений
53
54.
5455.
5556.
5657.
5758.
Как определить, что ДУ однородноеи использовать замену вида
смотрим тут
http://mathprofi.ru/odnorodnye_diffury_pervogo_poryadka.html
58




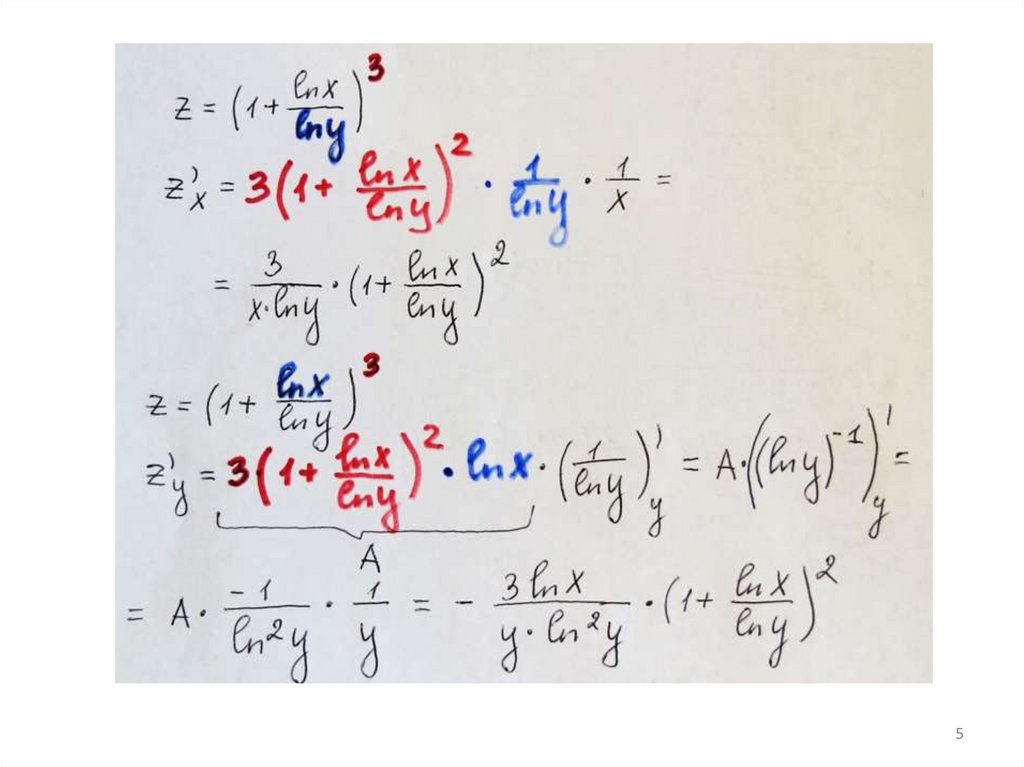

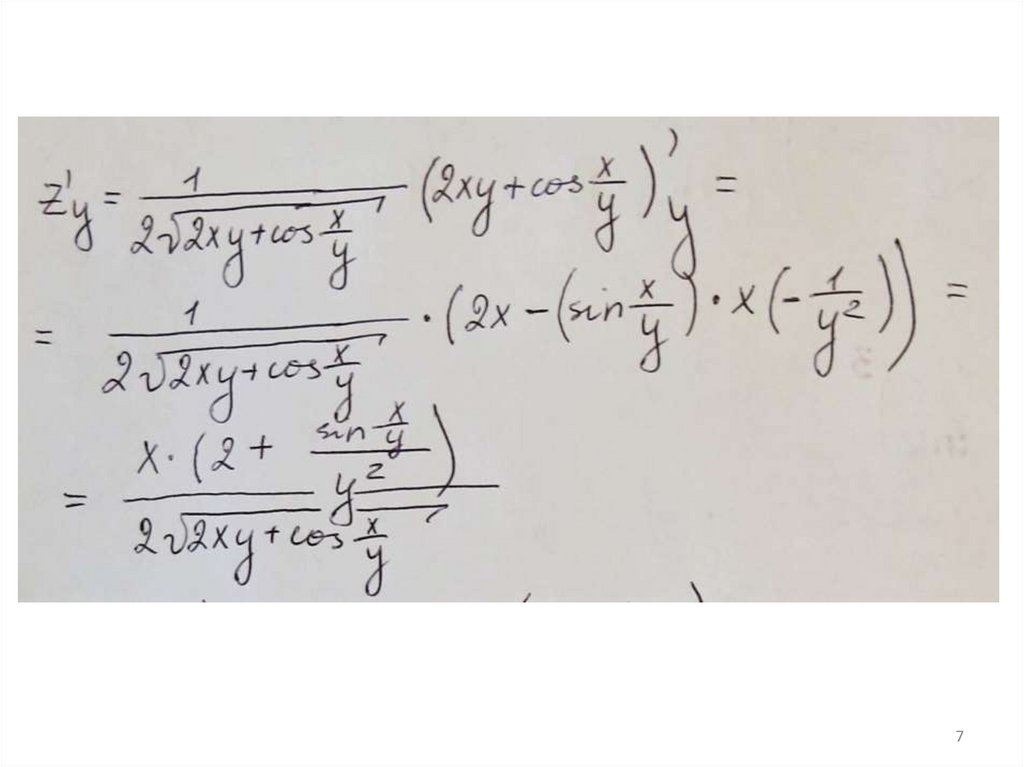
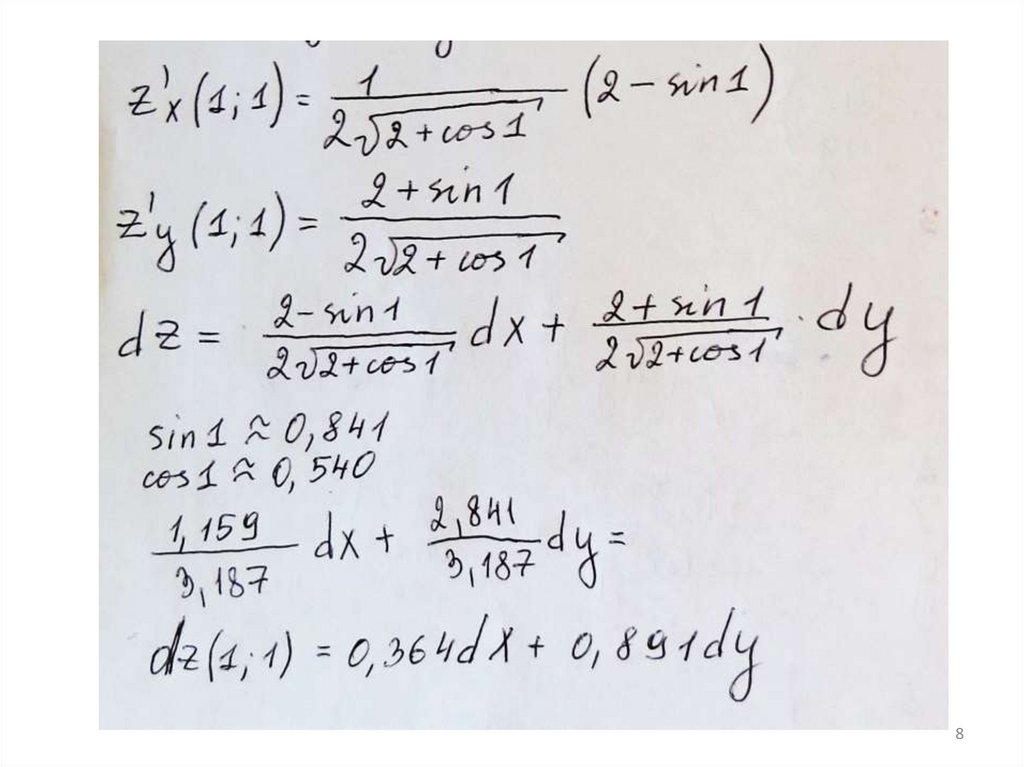
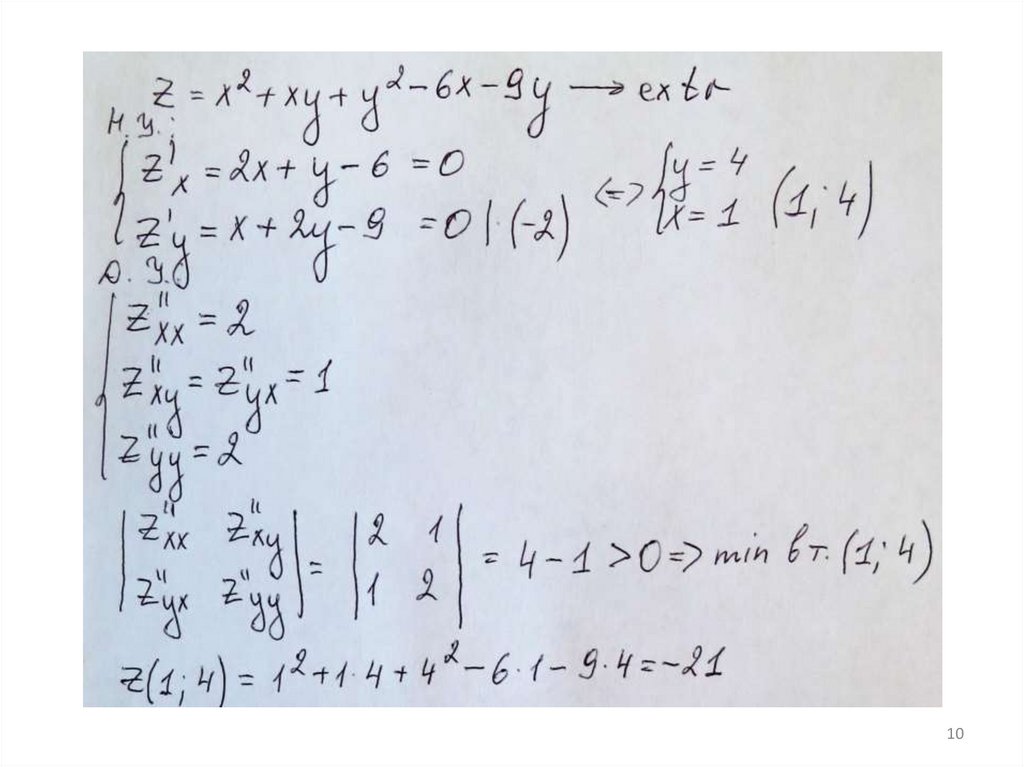

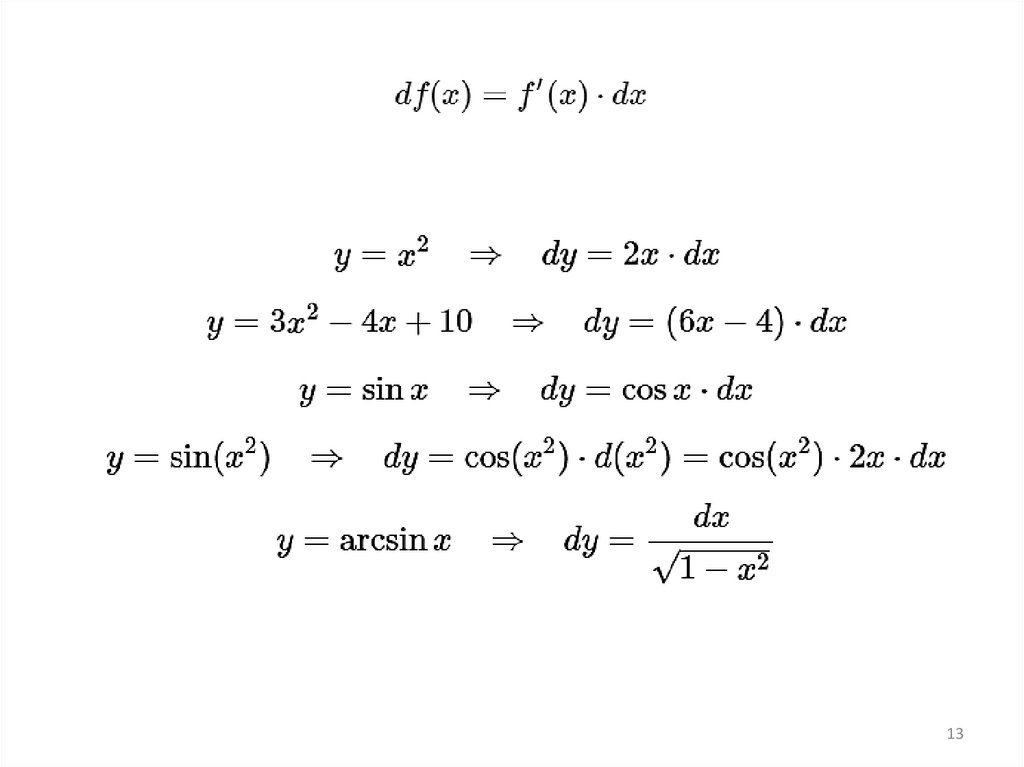


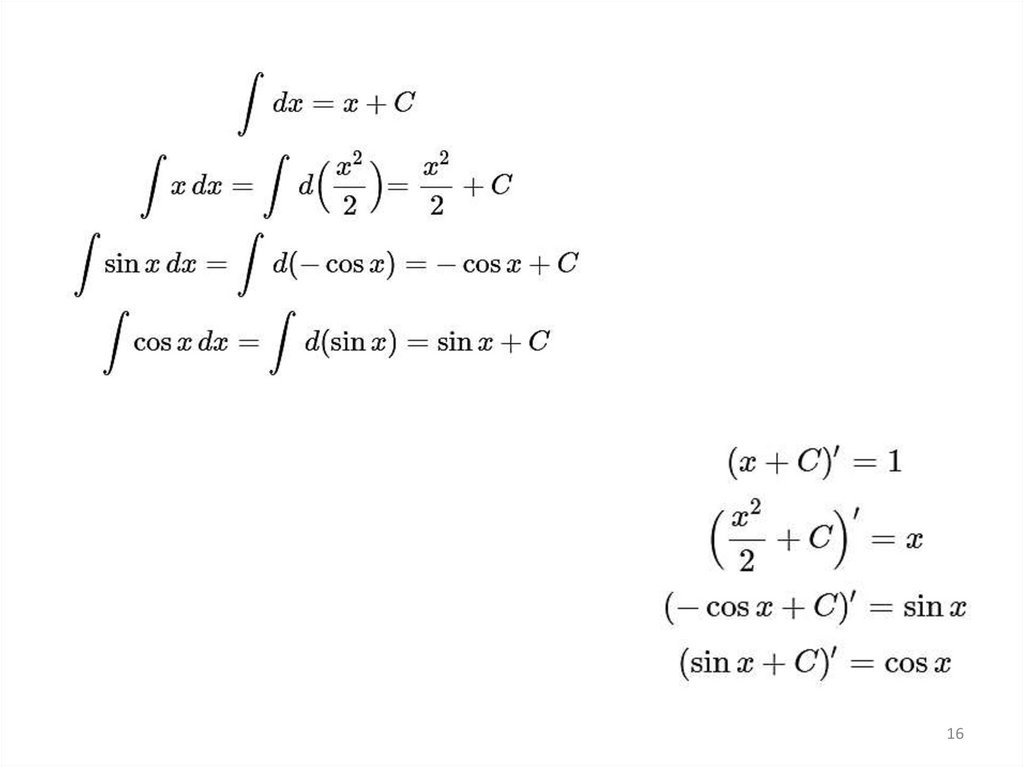








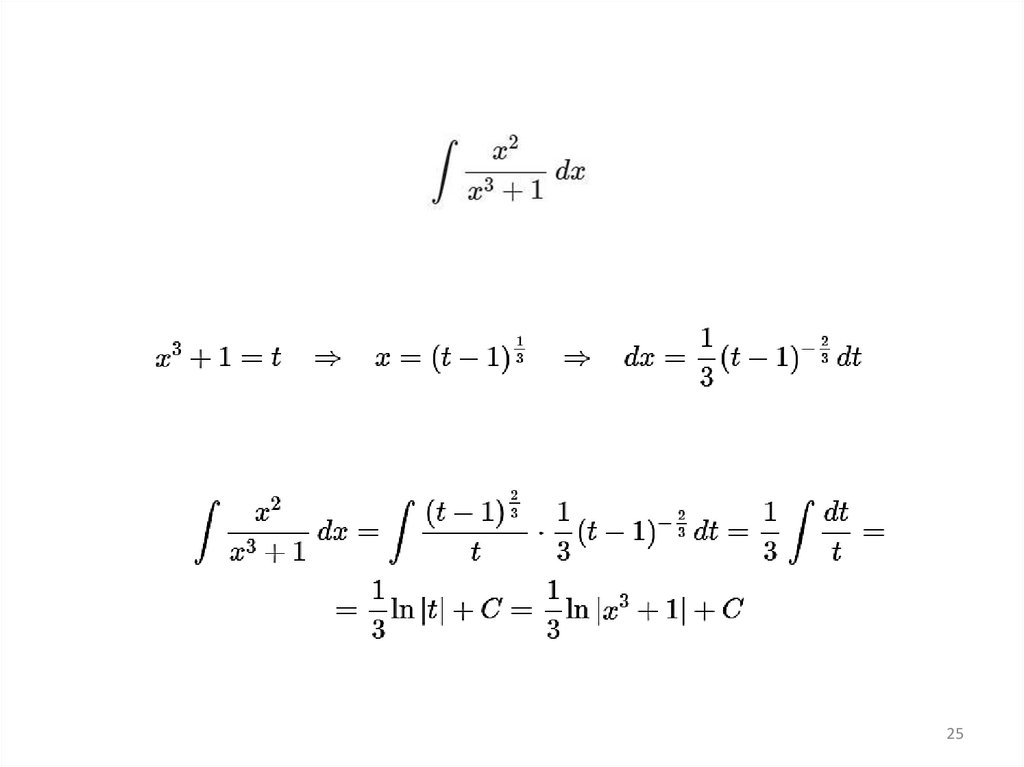

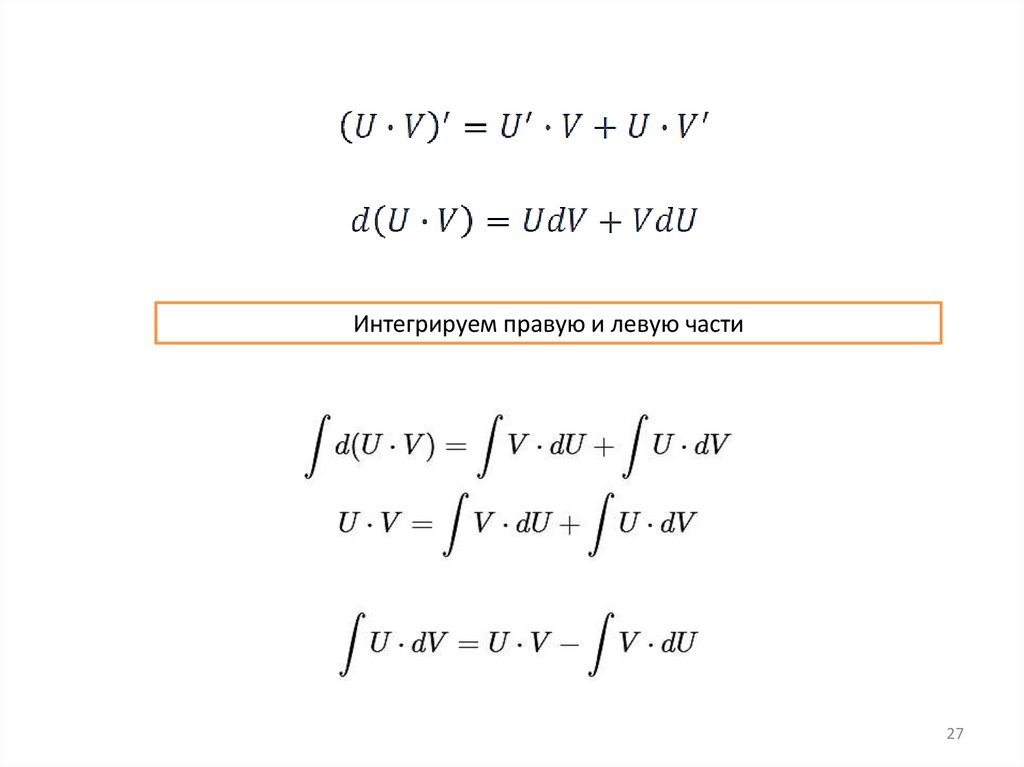

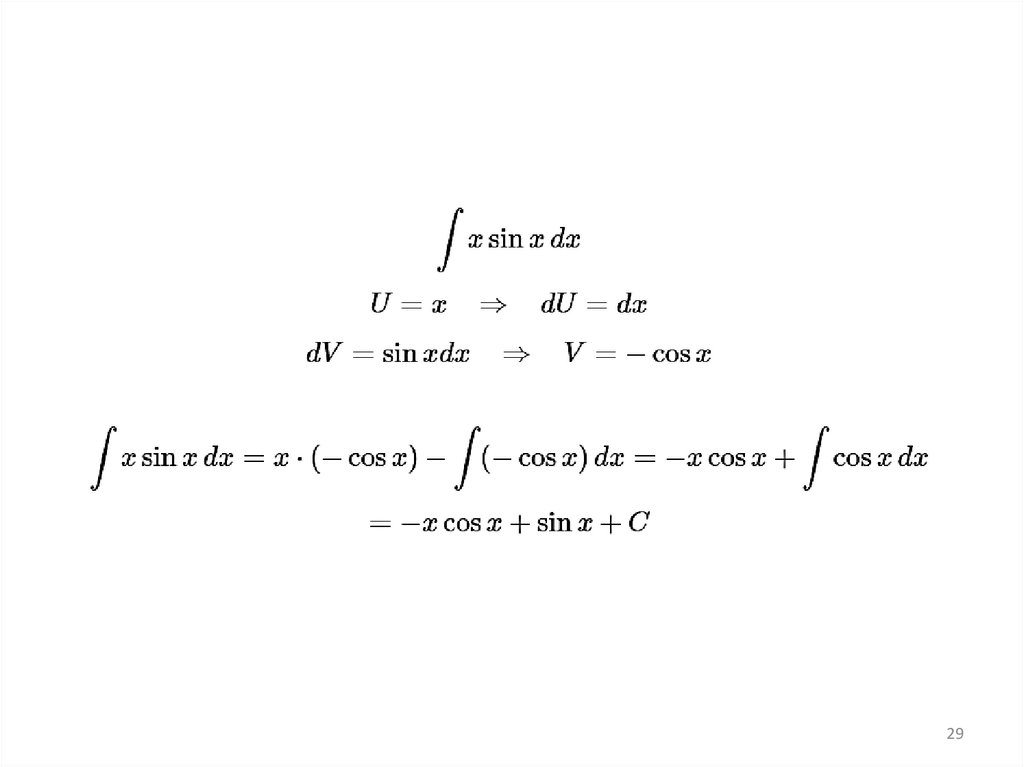













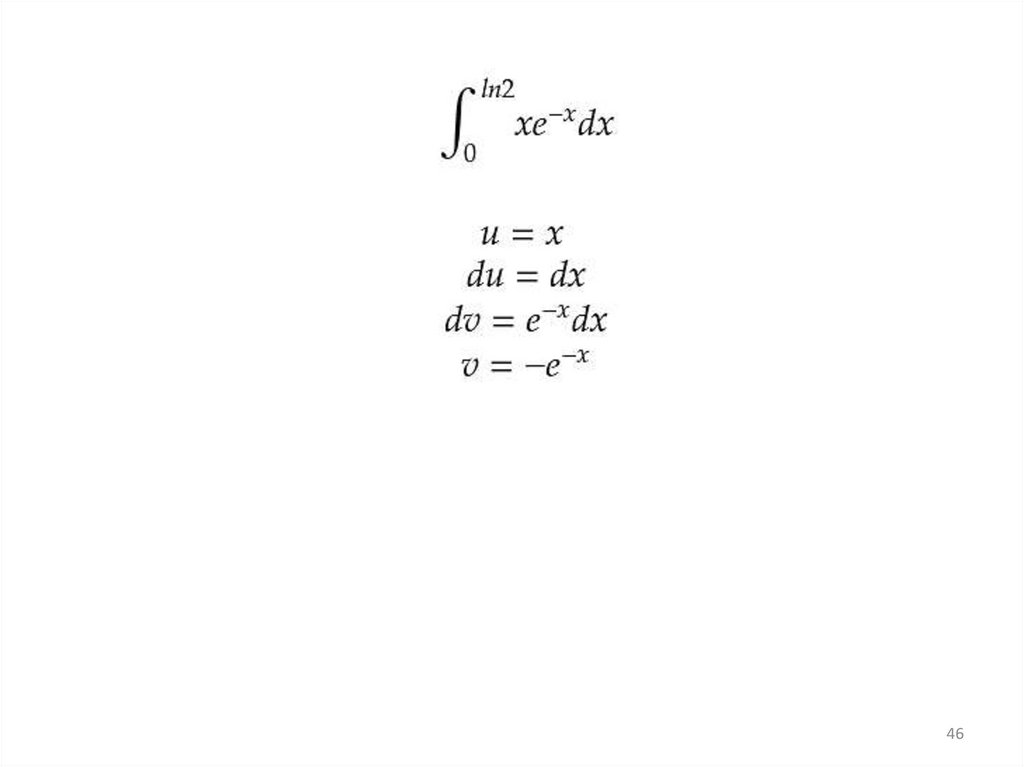











 mathematics
mathematics








