Similar presentations:
Производная функций нескольких переменных. Часть 2
1.
Вебинар «Производные функции несколькихпеременных, часть 2»
Введение в математический анализ
2.
План1.
2.
3.
4.
Разбор ДЗ.
Градиент.
Производная по направлению.
Условный экстремум – метод множителей
Лагранжа.
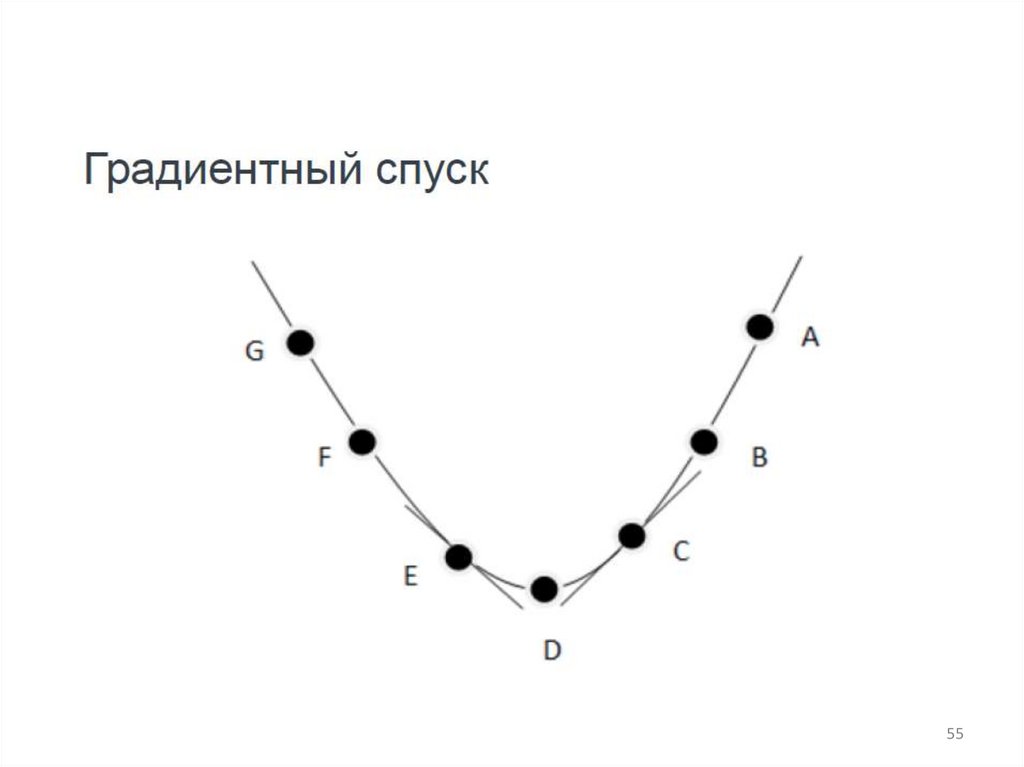
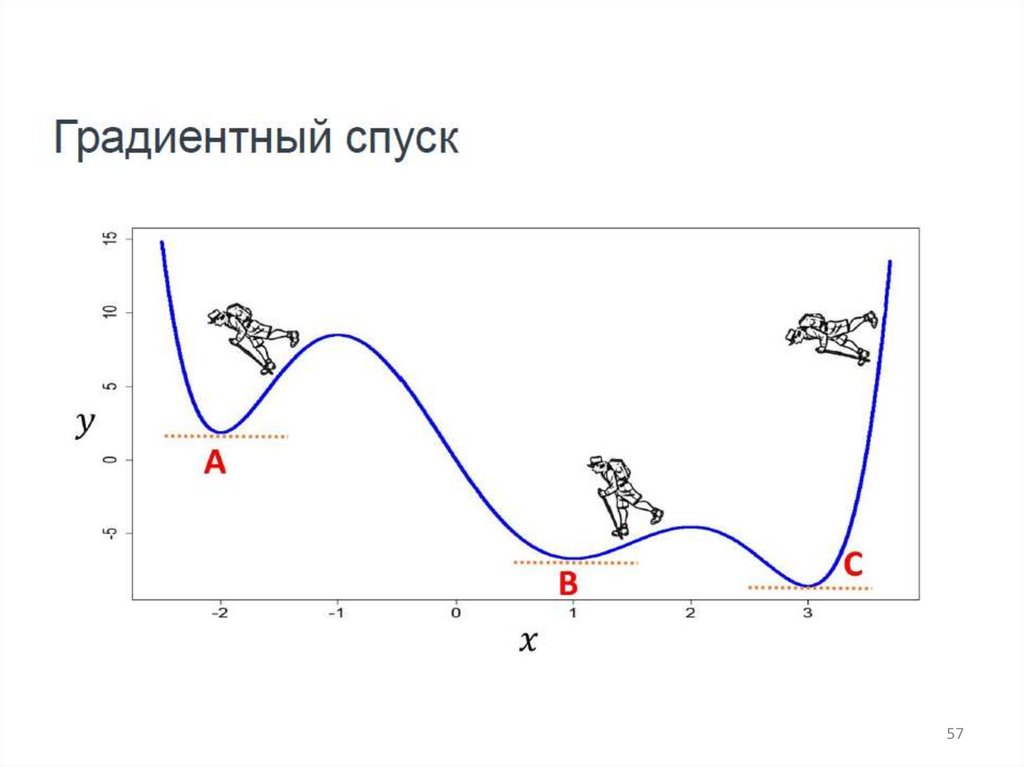
5. Градиентный спуск.
2
3.
По мотивам ДЗ❑Квадрат! Есть разница между (sinx)^2 и
sin(x^2).
❑ sin2, sin1, cos2 можно не упрощать, но можно
посчитать, используя ПО.
❑Единицы измерения угла:
▪ градусы (если есть значок);
▪ радианы – по умолчанию.
3
4.
45.
56.
2. Найти экстремумы функций (если они есть)1) y = |2x|
Необходимое условие: y'=|2x|/x=2|x|/x
в нуле производной не существует
Достаточное условие: производная функции существует в
окрестности точки и меняет свой знак при переходе через нее
0 - экстремум (минимум)
6
7.
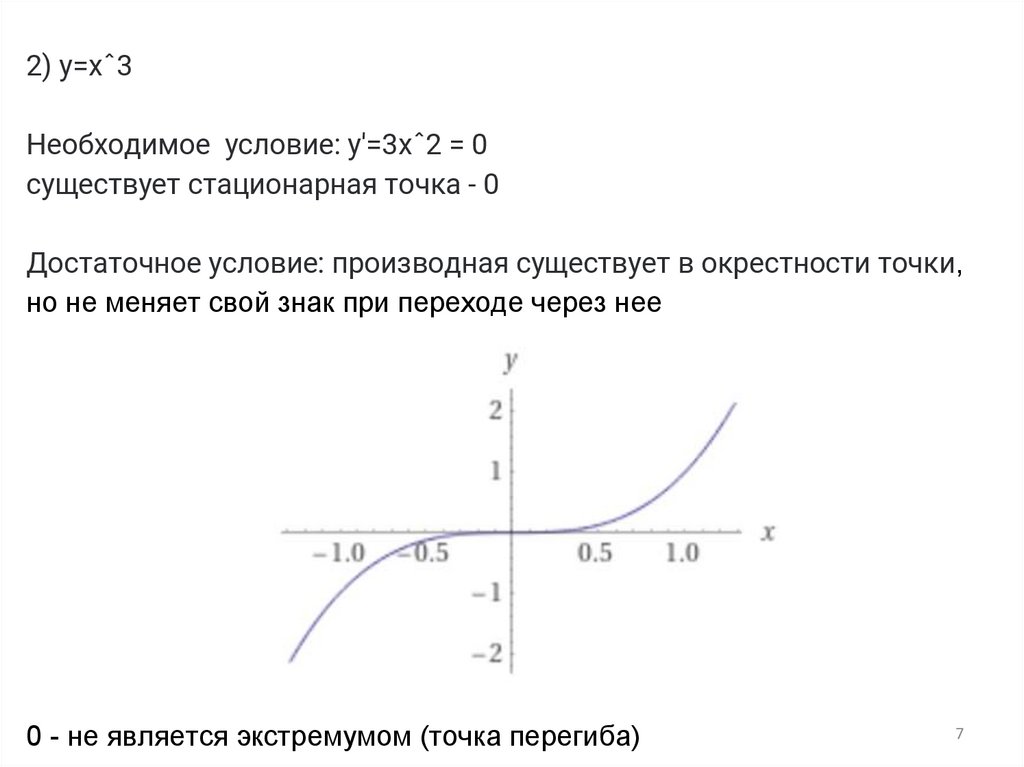
2) y=xˆ3Необходимое условие: y'=3xˆ2 = 0
существует стационарная точка - 0
Достаточное условие: производная существует в окрестности точки,
но не меняет свой знак при переходе через нее
0 - не является экстремумом (точка перегиба)
7
8.
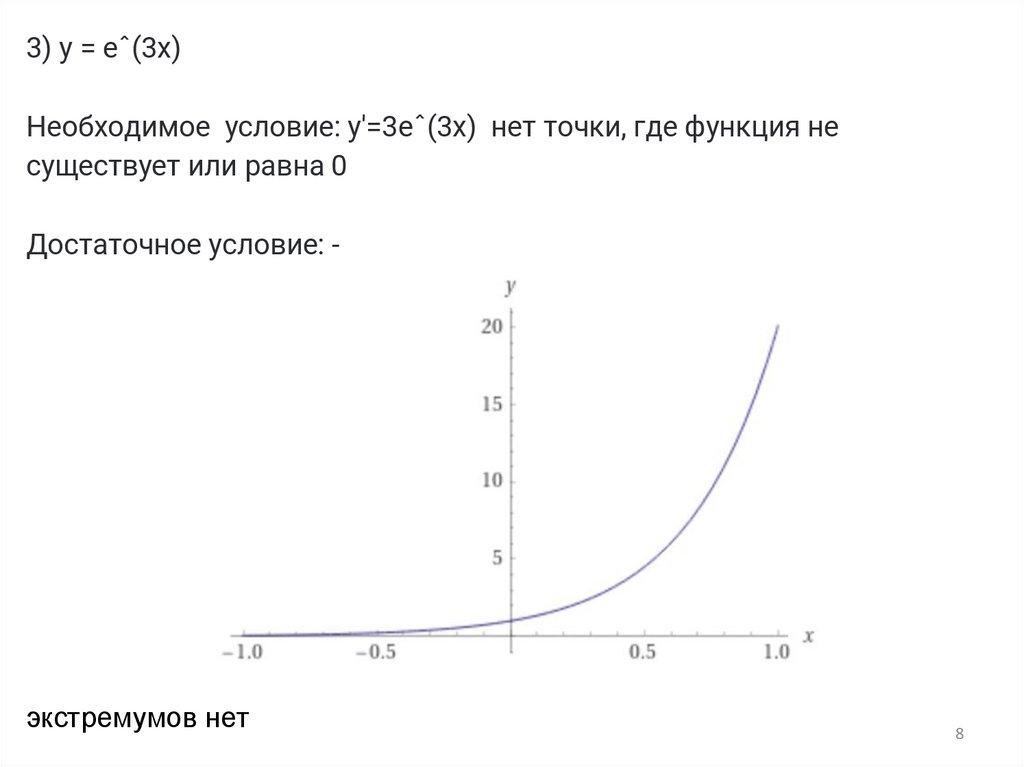
3) y = eˆ(3x)Необходимое условие: y'=3eˆ(3x) нет точки, где функция не
существует или равна 0
Достаточное условие: -
экстремумов нет
8
9.
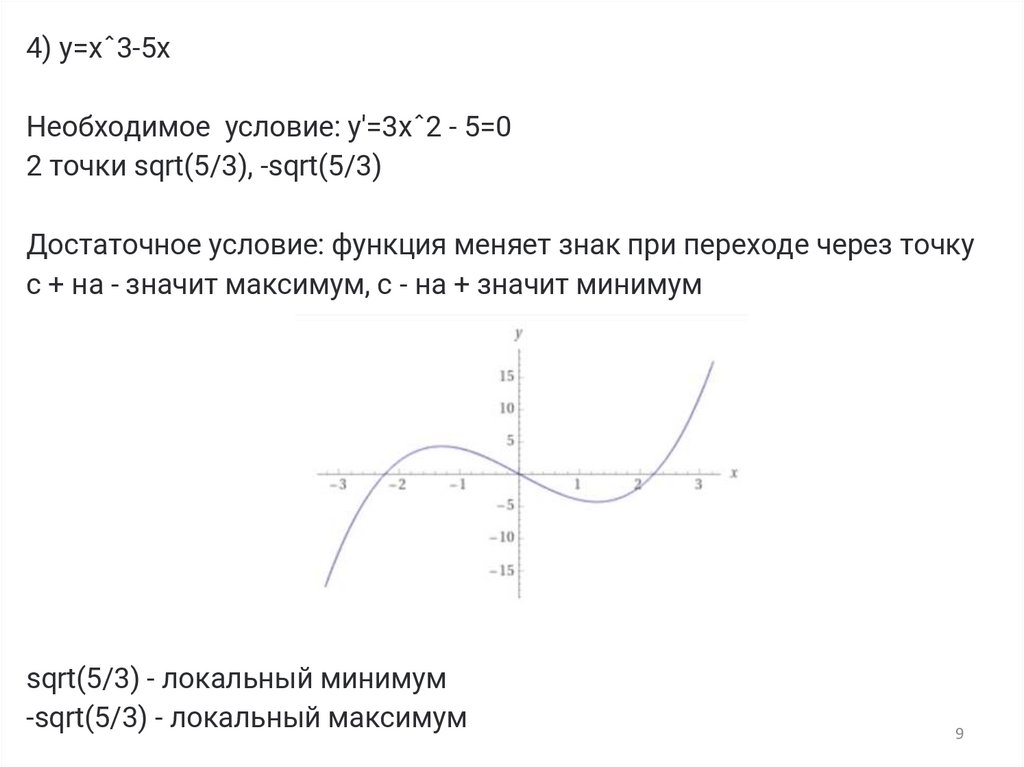
4) y=xˆ3-5xНеобходимое условие: y'=3xˆ2 - 5=0
2 точки sqrt(5/3), -sqrt(5/3)
Достаточное условие: функция меняет знак при переходе через точку
с + на - значит максимум, с - на + значит минимум
sqrt(5/3) - локальный минимум
-sqrt(5/3) - локальный максимум
9
10.
На прошлом вебинаре• Частные производные функций нескольких
переменных;
• Смешанные производные ФНП;
• Локальные экстремумы.
10
11.
Найти частные производныеZ=sinx/siny
• Z’(x)
• Z’(y)
11
12.
Найти частные производныеZ=sinx/siny
12
13.
ГрадиентОпределение
13
14.
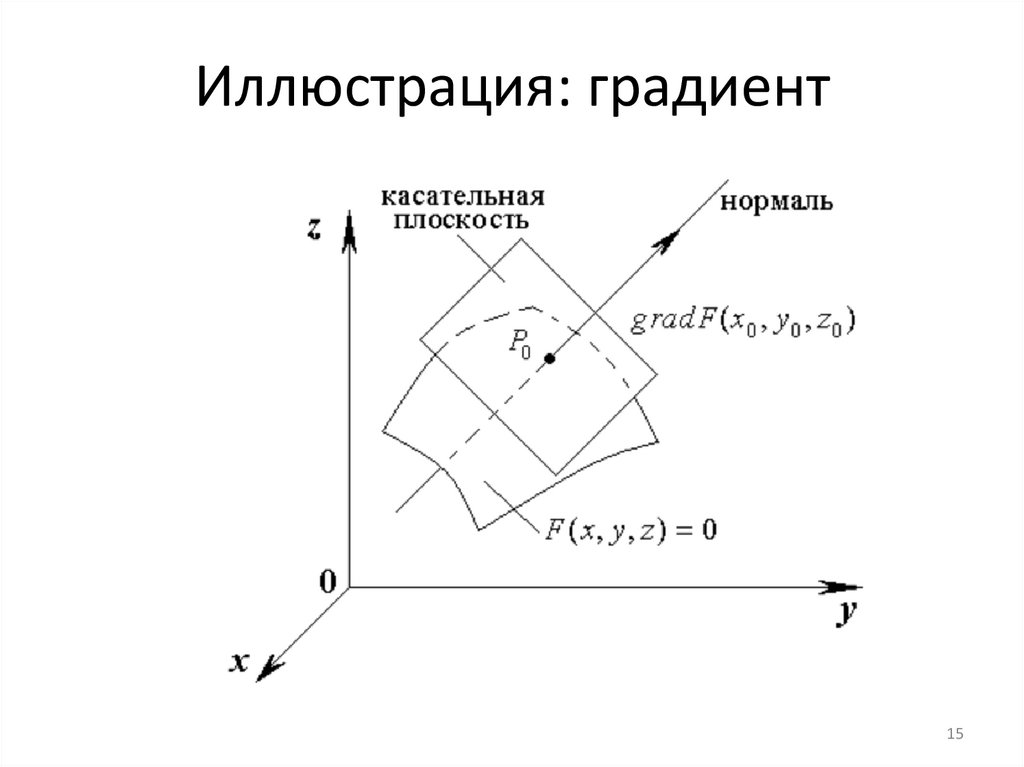
ГрадиентГрадиент - это вектор показывающий направление
наибольшего возрастания функции. Модуль вектора
градиента показывает скорость изменения функции.
14
15.
Иллюстрация: градиент15
16.
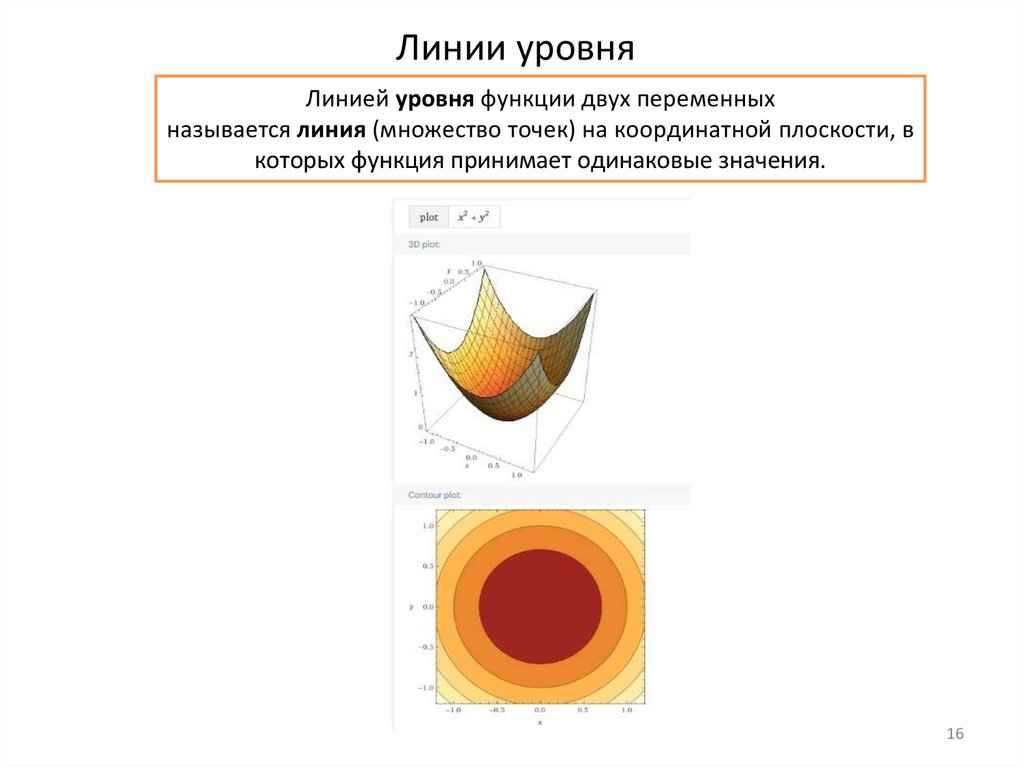
Линии уровняЛинией уровня функции двух переменных
называется линия (множество точек) на координатной плоскости, в
которых функция принимает одинаковые значения.
16
17.
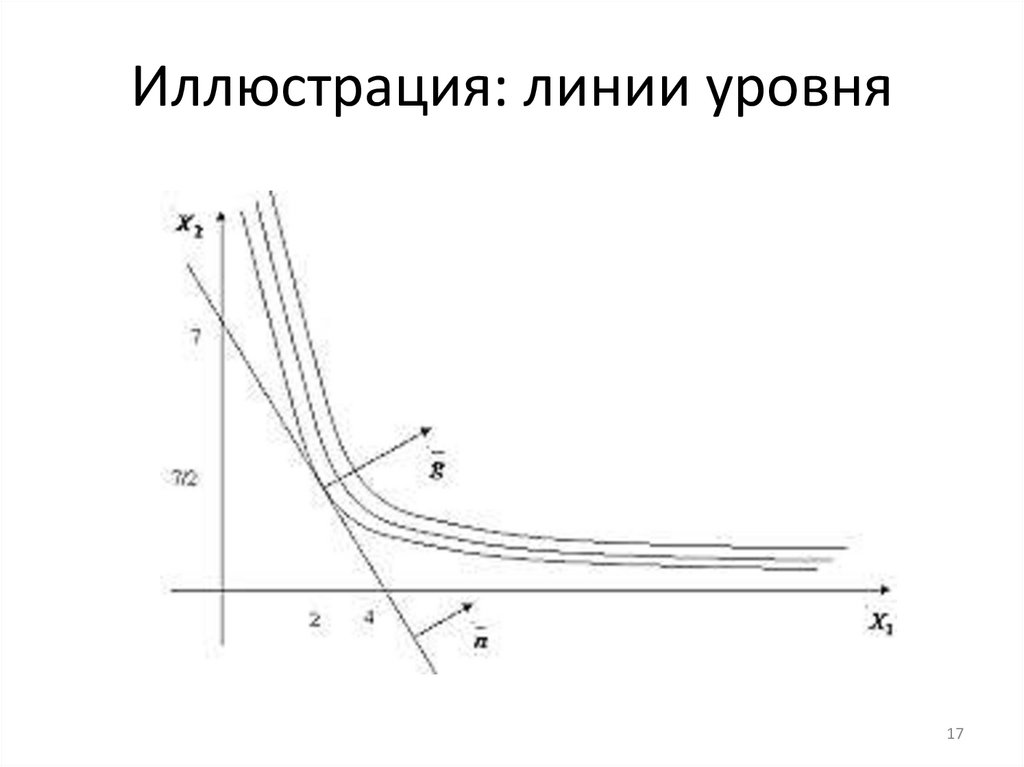
Иллюстрация: линии уровня17
18.
1819.
ГрадиентПример
19
20.
Производная по направлениюИсточник:
http://mathprofi.ru/proizvodnaja_po_napravleniju_i_gradient.
html
20
21.
Физический смысл производной понаправлению
21
22.
2223.
1. Найдём частные производные в точке М(1;2)23
24.
2. Найдём координаты направляющего вектора единичной длины24
25.
3. Вычисляем по формуле25
26.
В каком направлении у функциибудет наибольшая скорость роста?
26
27.
!Производная по направлениюградиента принимает наибольшее
значение!
68,77
27
28.
2829.
2930.
3031.
По мотивам прошлого вебинара31
32.
3233.
3334.
Квадратичная форма34
35.
3536.
3637.
*Полуопределенные квадратичныеформы
37
38.
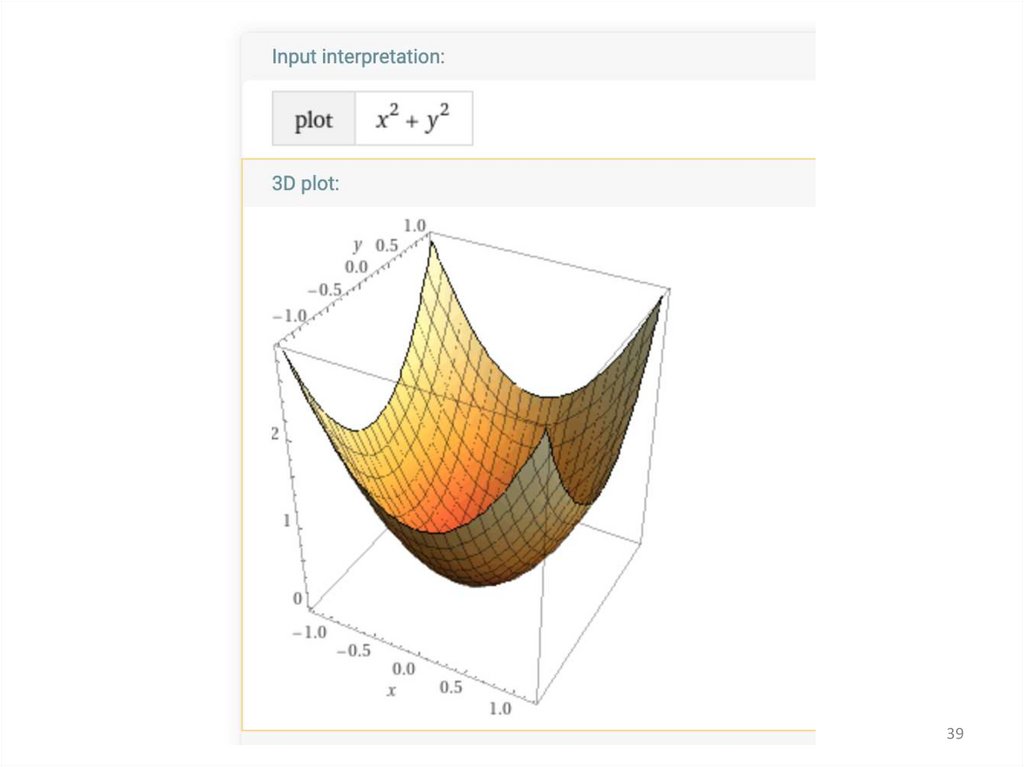
График38
39.
3940.
4041.
4142.
4243.
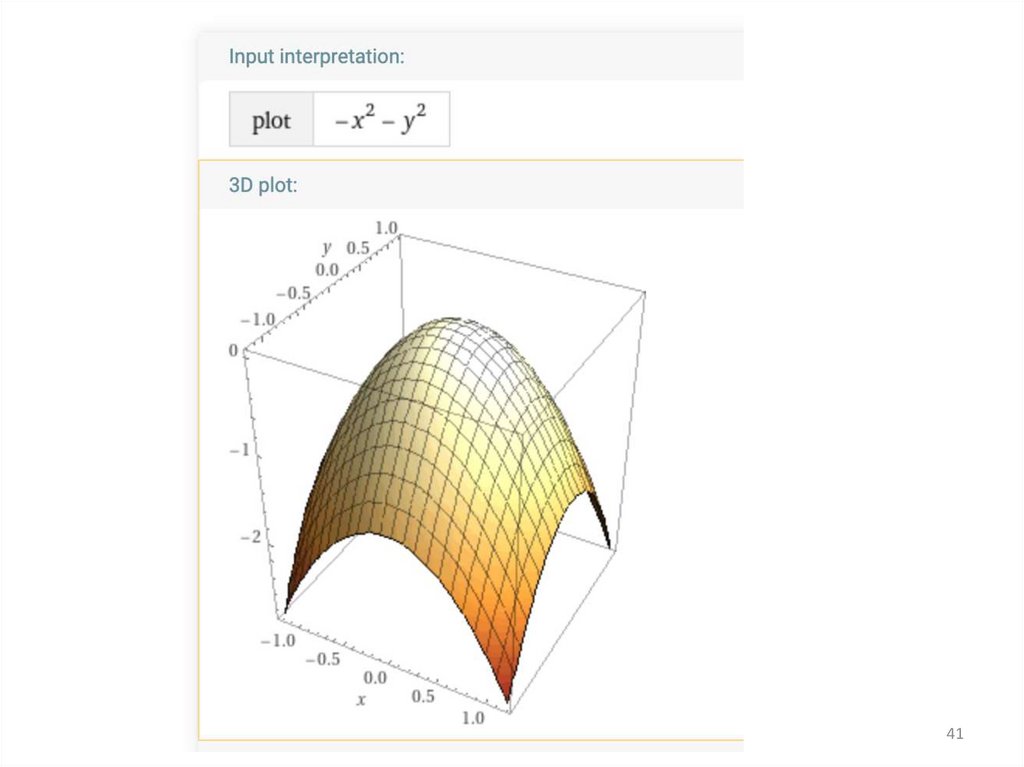
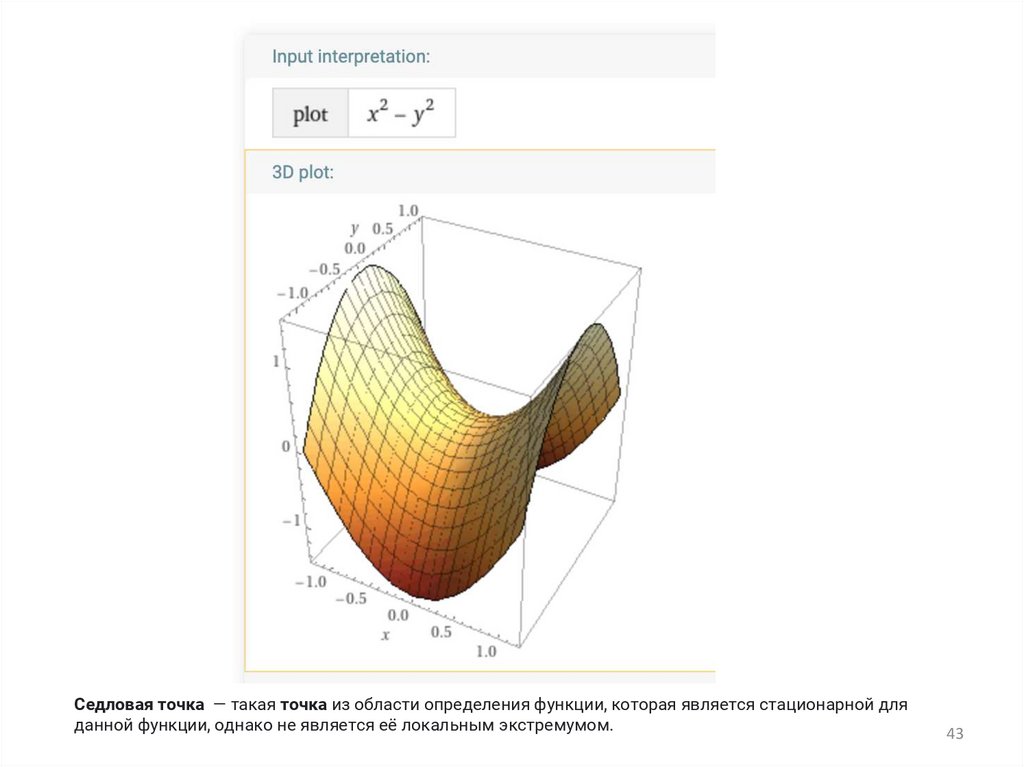
Седловая точка — такая точка из области определения функции, которая является стационарной дляданной функции, однако не является её локальным экстремумом.
43
44.
4445.
Исследование функции на условныйэкстремум
Функция Лагранжа
Необходимые условия экстремума
45
46.
Достаточные условия экстремумаЕсли в стационарной точке определитель матрицы A > 0, то в этой точке у
функции максимум.
Если в стационарной точке определитель матрицы A < 0, то в этой точке у
функции минимум.
46
47.
4748.
4849.
4950.
5051.
5152.
5253.
5354.
5455.
5556.
5657.
5758.
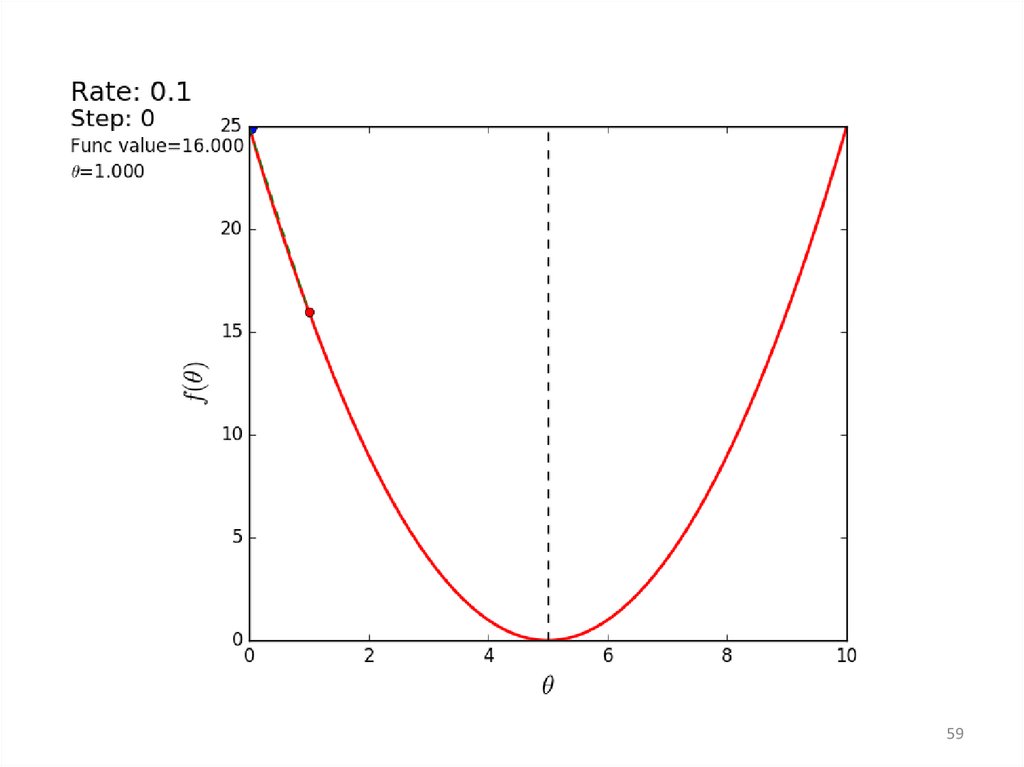
5859.
5960.
Реализация градиентного спуска• http://kayumov.ru/401/
60
61.
Проблема: «овражные» функциипример
61
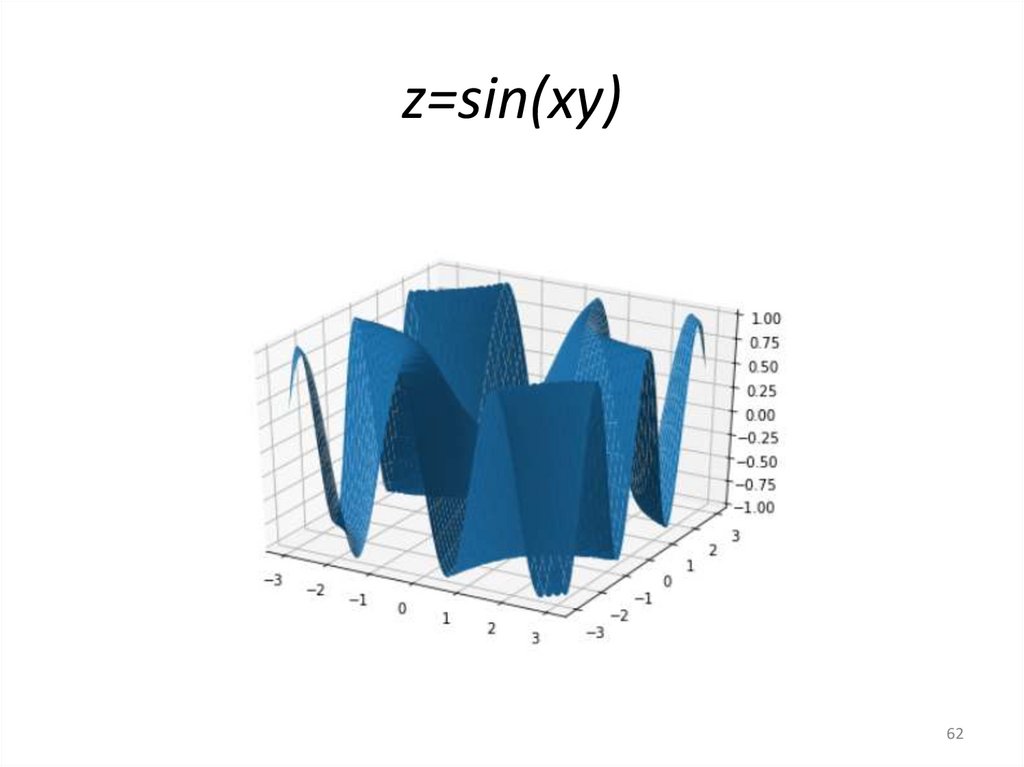
62.
z=sin(xy)62
63.
Имитация отжигаhttps://upload.wikimedia.org/wikipedia/commons/d/d5/Hill_Climbing_with_Simula
ted_Annealing.gif
63
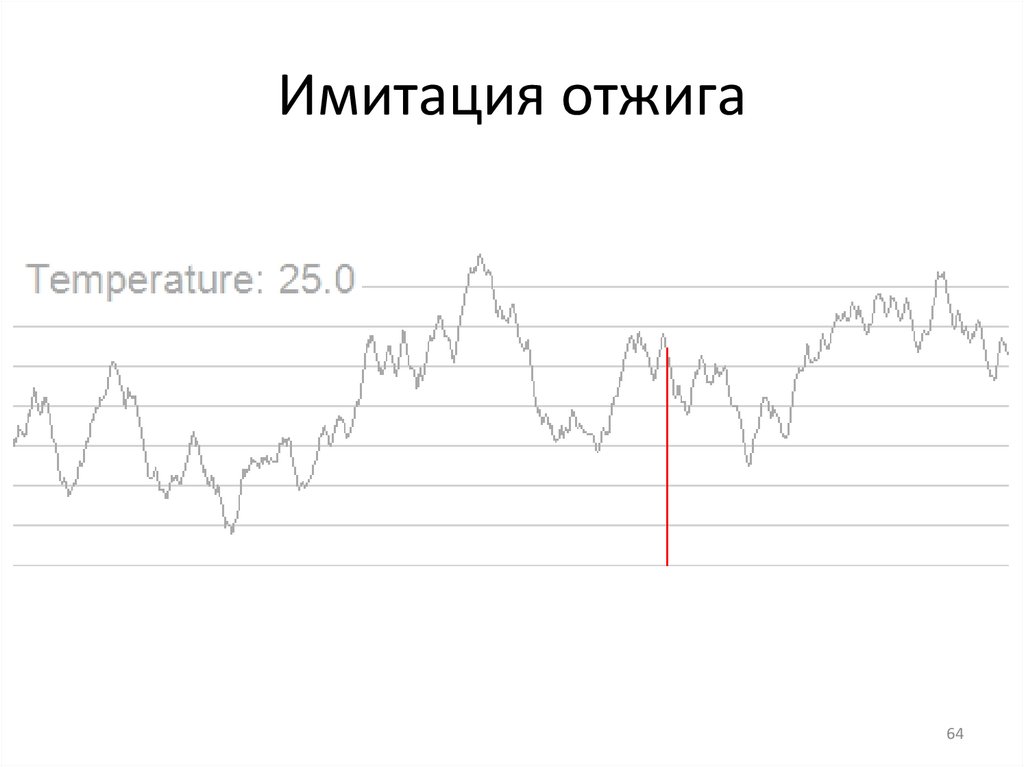
64.
Имитация отжига64
65.
Время вопросовСпасибо!
















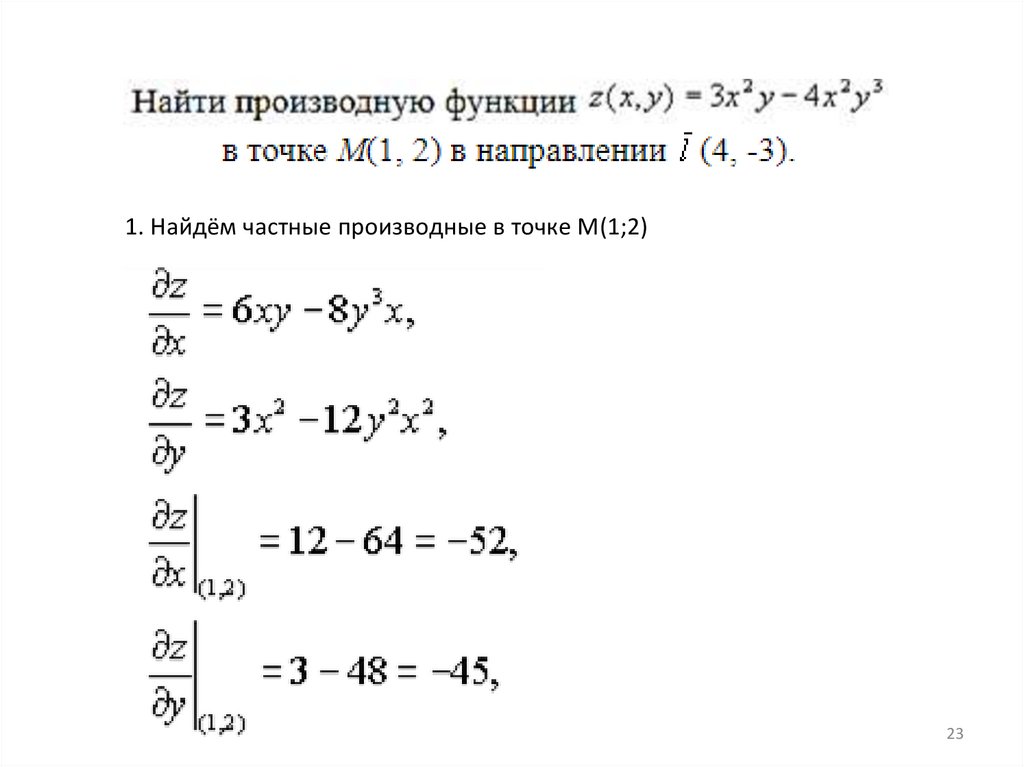





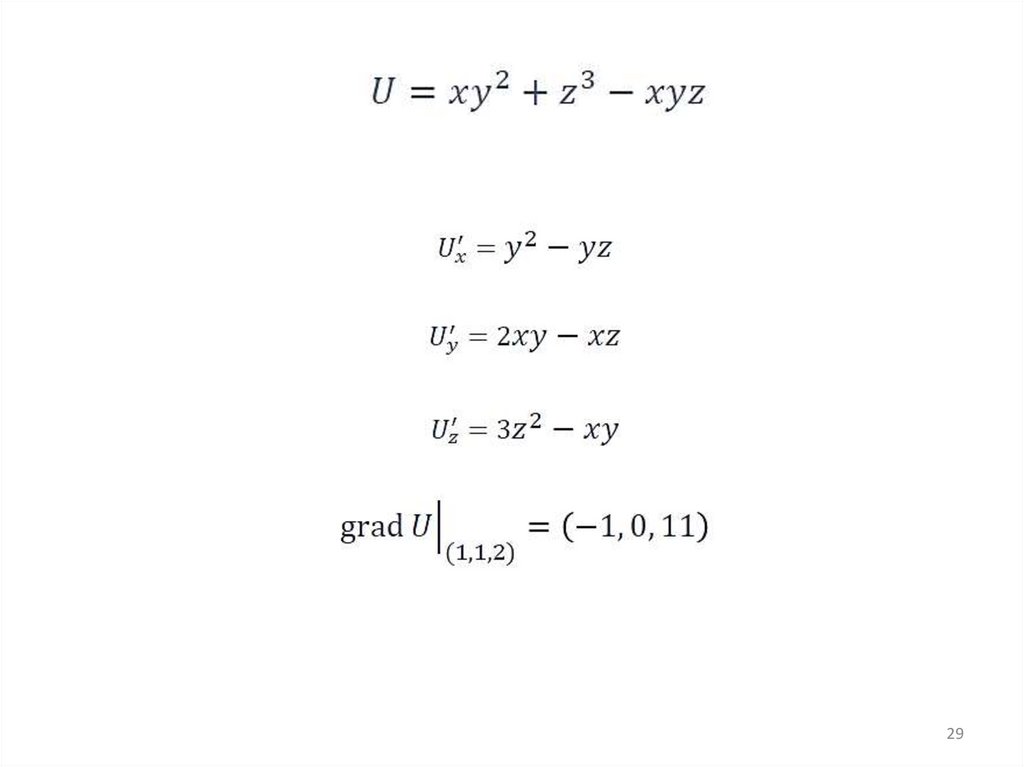
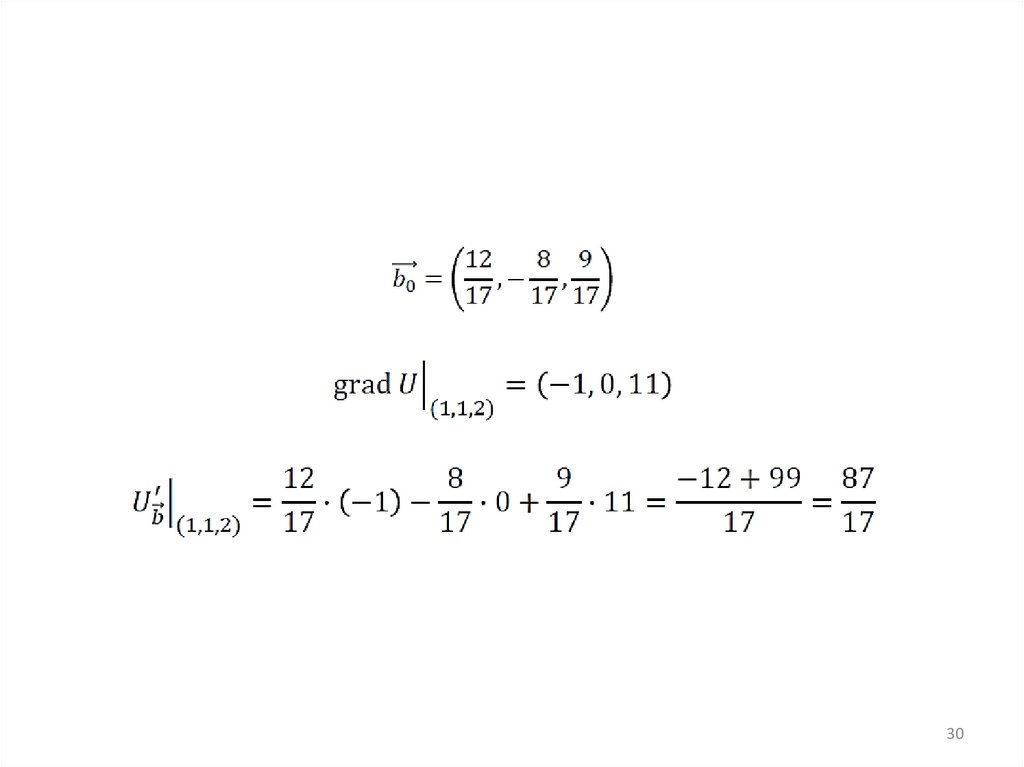








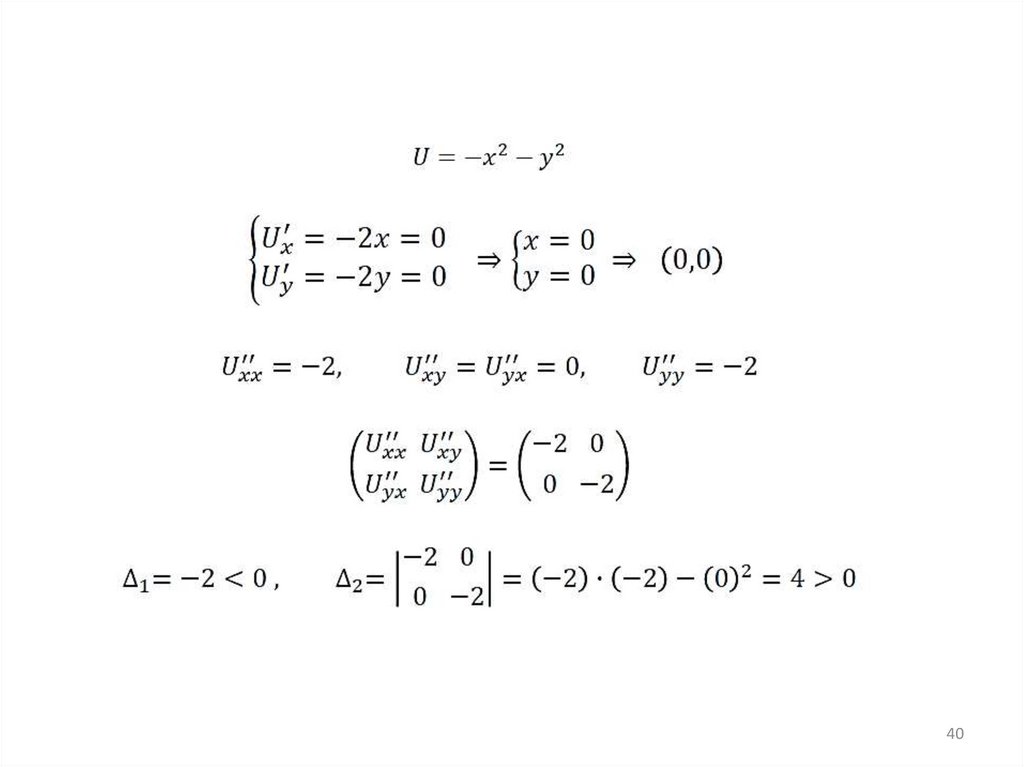
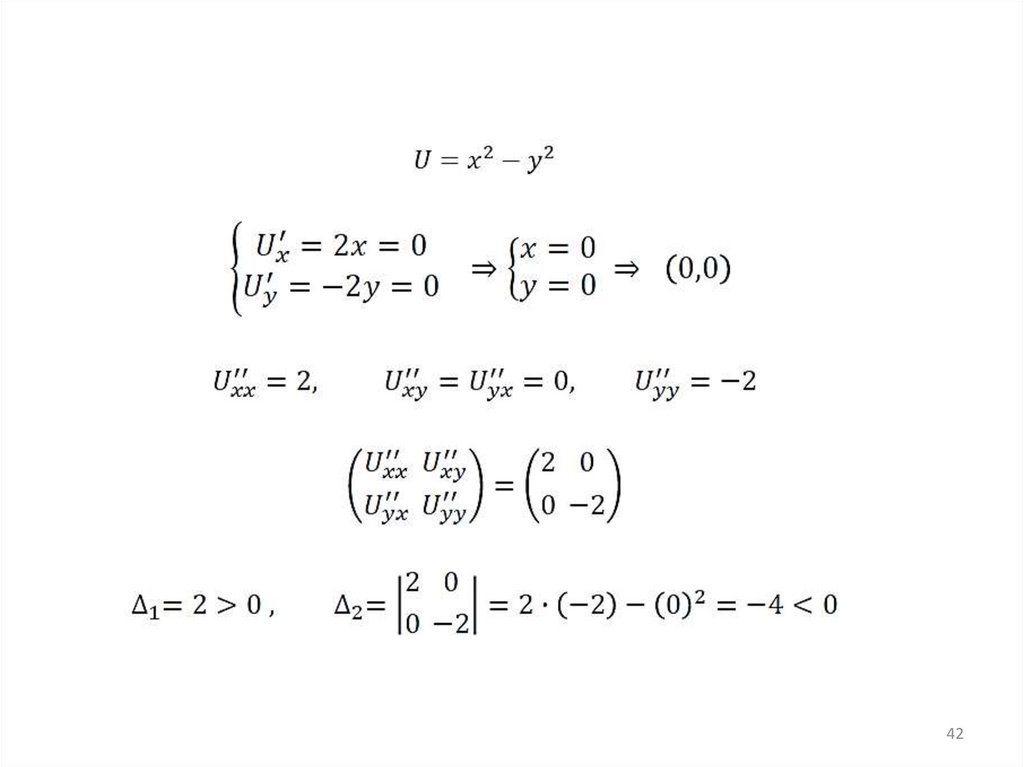

















 mathematics
mathematics








