Similar presentations:
Производные функции нескольких переменных (часть 1)
1.
Производные функциинескольких
переменных (часть 1)
Введение в математический анализ
2.
План1. Разберём ДЗ
2. Несколько слов о математическом моделировании.
3. Функции 2-х переменных; функции многих
переменных.
4. Частные производные, дифференциалы функций.
5. Экстремум функции 2-х переменных.
6. Аппроксимация. МНК.
2
3.
Разбор ДЗ по теме «Производныеодной переменной»
3
4.
45.
56.
67.
Задание 2= - sin(pi + 3*sqrt(pi))(2*sqrt(pi)+3) =
= sin(3*sqrt(pi))(2*sqrt(pi)+3) =
= -5,38 (с округлением)
7
8.
Задание 38
9.
910.
Задание 410
11.
Функции многих переменных.Где применяется математическое
моделирование?
Модели потребительского выбора, фирмы
(производственные функции);
экономического роста; равновесия на
товарных, факторных и финансовых рынках и
т. д.
Механика жидкости - нефтедобывающая
промышленность.
11
12.
Математическое моделирование –зачем?
• Упрощенно описать реальность.
• Учесть ключевые факторы.
• Принять решение.
• Математическая модель – основа для
принятия решения.
12
13.
Задачи математическогопрограммирования
Решают: проблему выбора, оптимизации.
У истоков: Канторович, Кун, Таккер.
13
14.
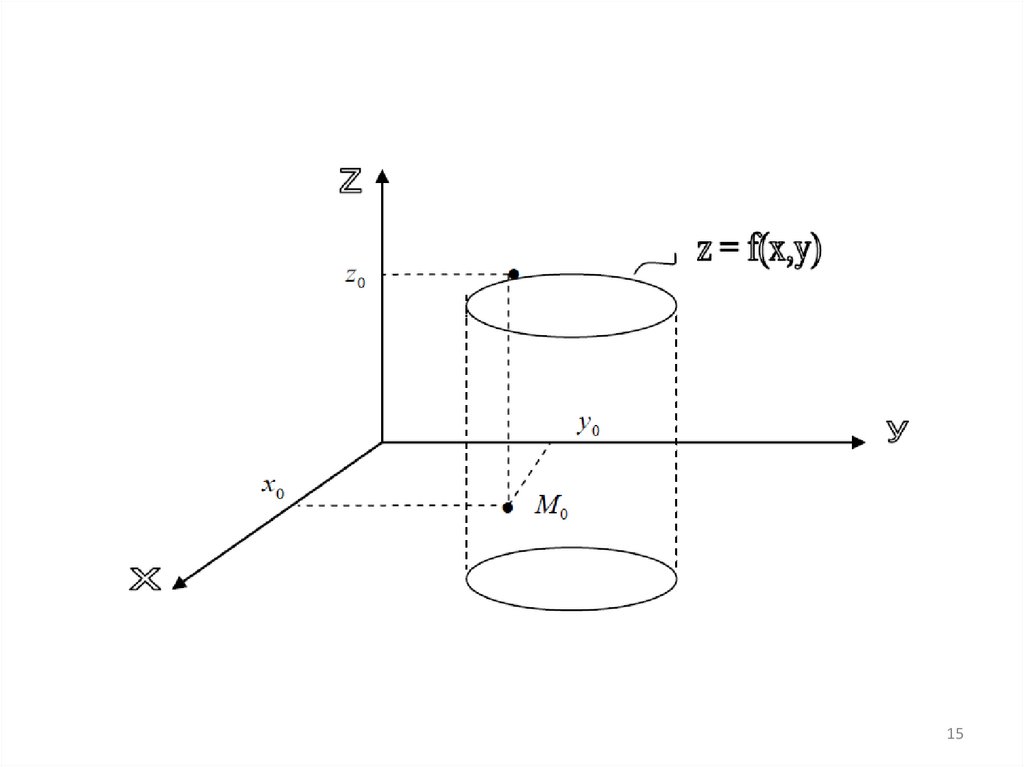
Функция 2-х переменных:определение.
График функции - поверхность
14
15.
1516.
Область определения функции 2-хпеременных D(x;y)
16
17.
Примеры поверхностей 2-го порядка17
18.
Пример18
19.
Пример19
20.
ПримерD(x;y)
Круг радиуса 1 в центре с началом координат
20
21.
Функция многих переменных:определение.
21
22.
Частные производные 1-го порядка- «дельта икс», приращение переменной x
=
- «дельта игрек», приращение переменной у
22
23.
2324.
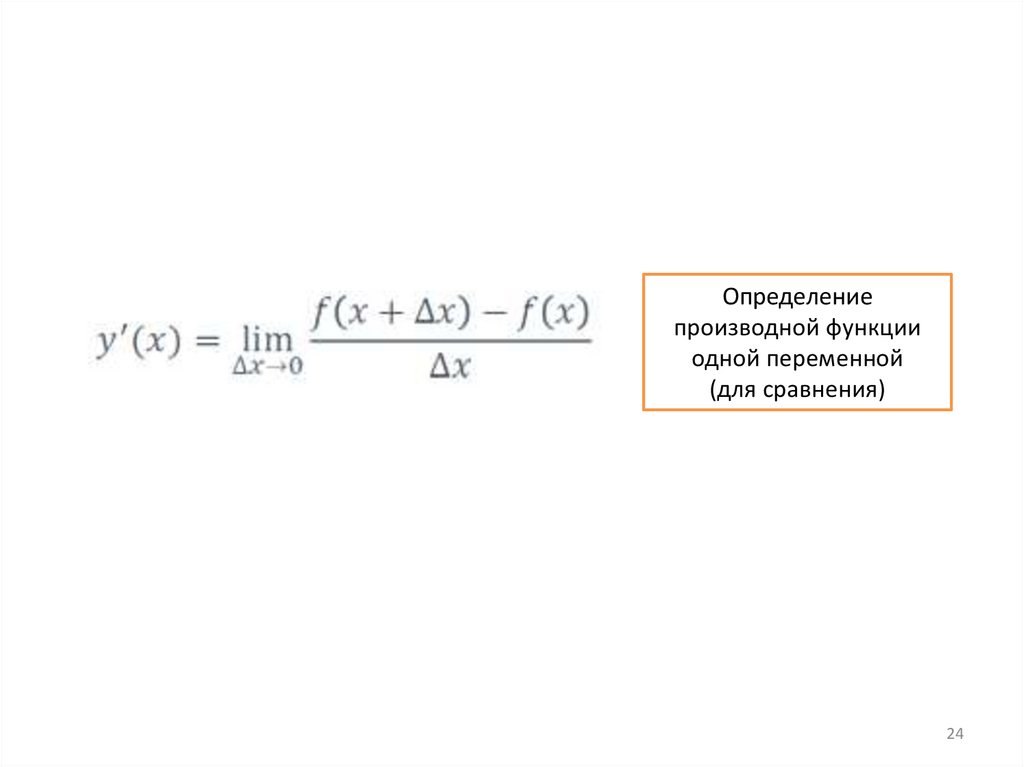
Определениепроизводной функции
одной переменной
(для сравнения)
24
25.
Вычисление частных производных25
26.
Сравнение с неявными функциямиВ случае неявной функции y зависит от х: y(x)
В случае функции нескольких переменных – нет: z(x,y)
26
27.
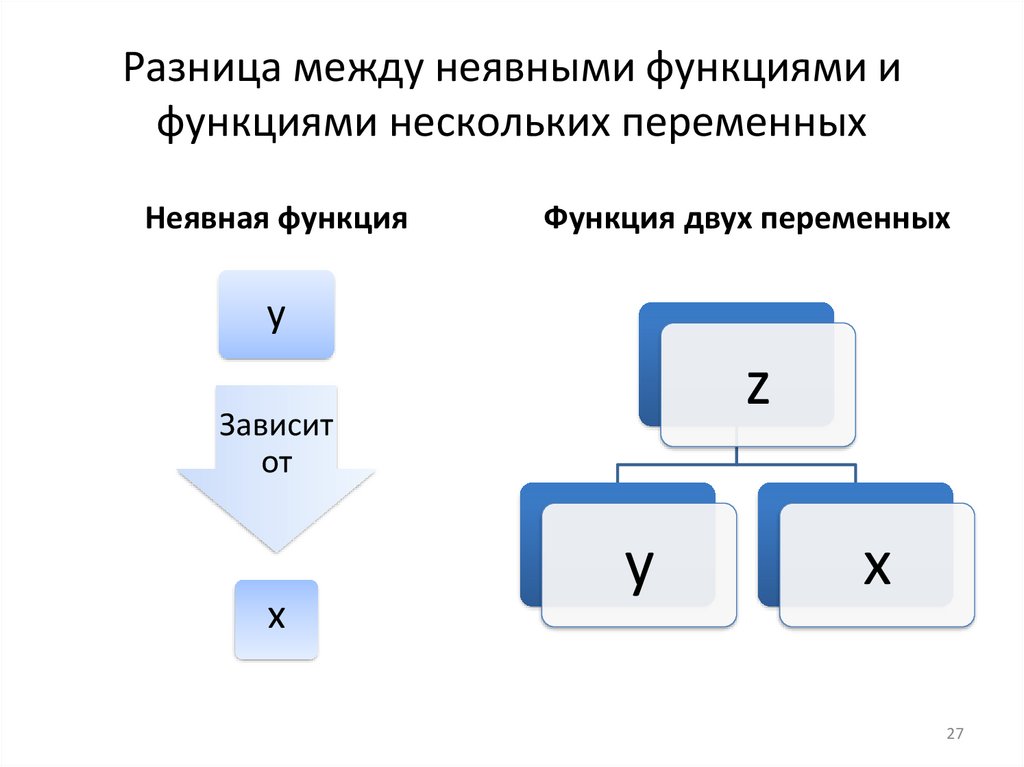
Разница между неявными функциями ифункциями нескольких переменных
Неявная функция
Функция двух переменных
у
z
Зависит
от
y
x
27
х
28.
Вычислить:28
29.
Вычисление частных производных29
30.
3031.
Частный дифференциал функциимногих переменных W(x,y,z)
dx – «дифференциал икс» - произвольное бесконечно малое приращение
переменной величины
31
32.
Частный дифференциал не путаем счастной производной функции
многих переменных
Частный дифференциал равен частной
производной умноженной на приращение
32
33.
Полный дифференциал функциимногих переменных W(x,y,z)
33
34.
Полный дифференциал функциимногих переменных W(x,y,z)
34
35.
3536.
dW = W’(x)dx+W’(y)dy+W’(z)dzdW=(2cos(2x)+cos(5y))dx5xsin(5y)dy-(7/(cos(7z)^2)dz
dW(0;0;0)=3dx-7dz
36
37.
dW (0;0;0) = 3dx-7dzИнтерпретация
В точке (0;0;0) при бесконечно малых
приращениях x, y и z главную линейную часть
приращения функции W можно вычислить по
формуле.
37
38.
Частные производные 2-го порядка38
39.
Частные производные 2-го порядка39
40.
4041.
4142.
4243.
4344.
4445.
4546.
4647.
Экстремум функции 2-х переменных47
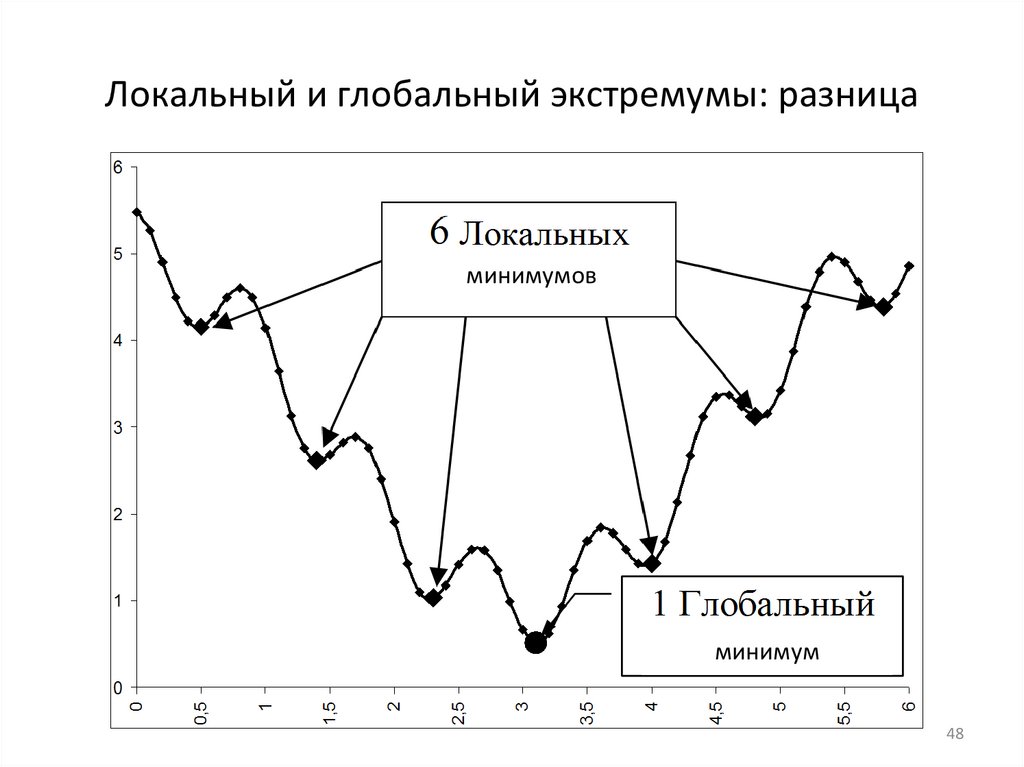
48.
Локальный и глобальный экстремумы: разницаминимумов
минимум
48
49.
Найти наибольшее и наименьшее значенияфункции на заданном отрезке
http://mathprofi.ru/naibolshee_i_naimenshee_znacheniya_funkcii_na_otrezke.html
(пример 3)
49
50.
Экстремум функции 2-х переменныхНеобходимые условия экстремума.
Частные производные равны нулю или не существуют.
Точки, для которых это выполняется, называются критическими.
Точки, в которых производная равна 0, называются стационарными.
Технически – решаем систему уравнений
Важно!
Не каждая критическая точка является точкой экстремума.
Аналог для функций одной переменой: точки перегиба (y = x3 )
50
51.
Необходимые условия экстремумафункции нескольких переменных
z’x=0
z’y=0
(для стационарных точек)
51
52.
Достаточное условие экстремума(для стационарных точек)
1
2
Минимум
Максимум
52
53.
Определитель матрицы 2х253
54.
К достаточному условию есть несколькоподходов
Два математических:
• через полный дифференциал второго порядка
(требует большого навыка работы с числами);
• через уравнения касательной плоскости (является
самым сложным способом, но при этом самым
надежным).
Два алгебраических:
• через критерий Сильвестра (с помощью матрицы
Гёссе. Является самым простым способом, но требует
начального уровня знания в линейной алгебре);
• через собственные значение матрицы Гёссе
(является самым быстрым, но требует более
глубокого уровня знания в линейной алгебре).
54
55.
Пример: исследовать на экстремумфункцию
55
56.
Необходимые условия56
57.
Достаточные условия (частный случайкритерия Сильвестра)
М1 (0;0)
М2 (1;0.5)
57
58.
Источник: www.linis.ru58
59.
Комментарий к записи59
60.
Аппроксимация60
61.
• Интерполяция — способ нахожденияпромежуточных значений величины по
имеющемуся дискретному набору
известных значений.
• Экстраполяция — способ построения
функции вне интервала известных
значений.
61
62.
6263.
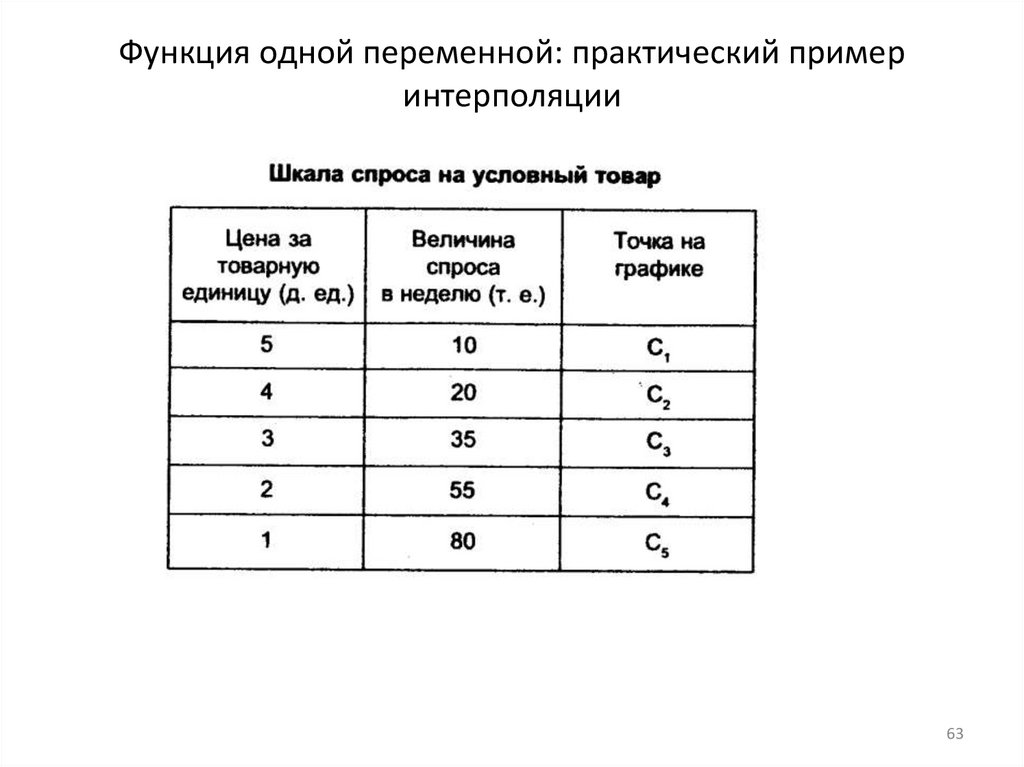
Функция одной переменной: практический примеринтерполяции
63
64.
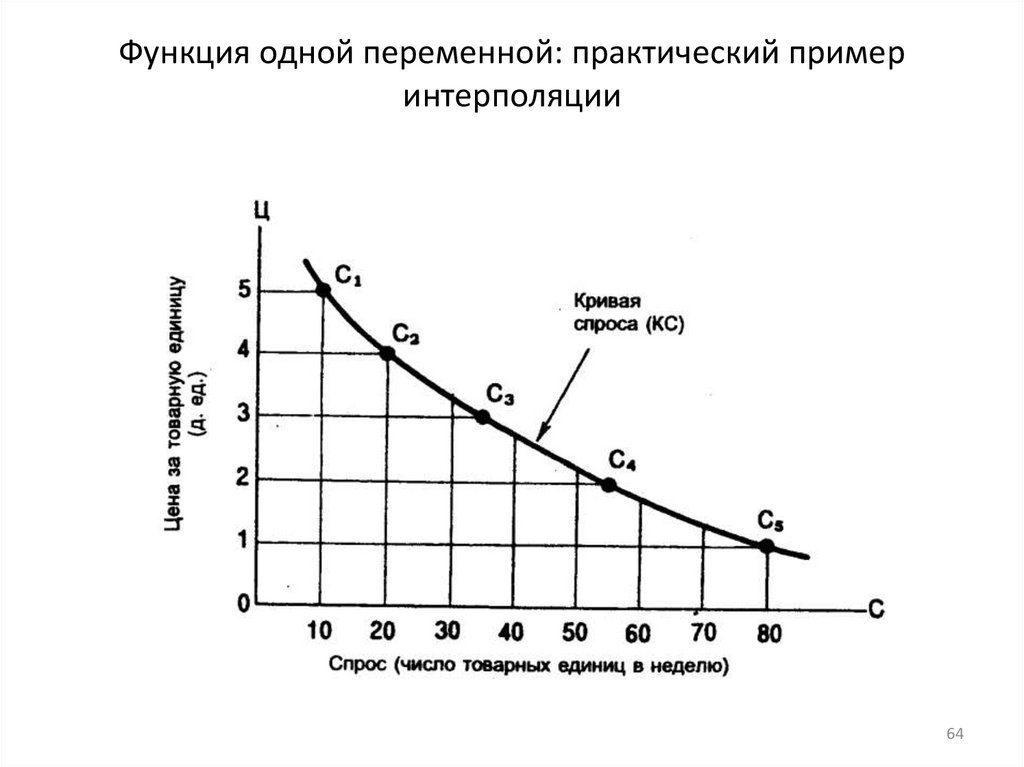
Функция одной переменной: практический примеринтерполяции
64
65.
6566.
6667.
6768.
МНК68
69.
6970.
7071.
Оценка качества модели:коэффициент детерминации
Находится в диапазоне от 0 до 1;
Чем ближе к 1, тем лучше модель.
71
72.
МНК для нелинейных функцийВзвешенный МНК
Обобщённый МНК
И т. д.
72
73.
МНК для нелинейных функций73
74.
МНК для нелинейных функций74
75.
Спасибо!75



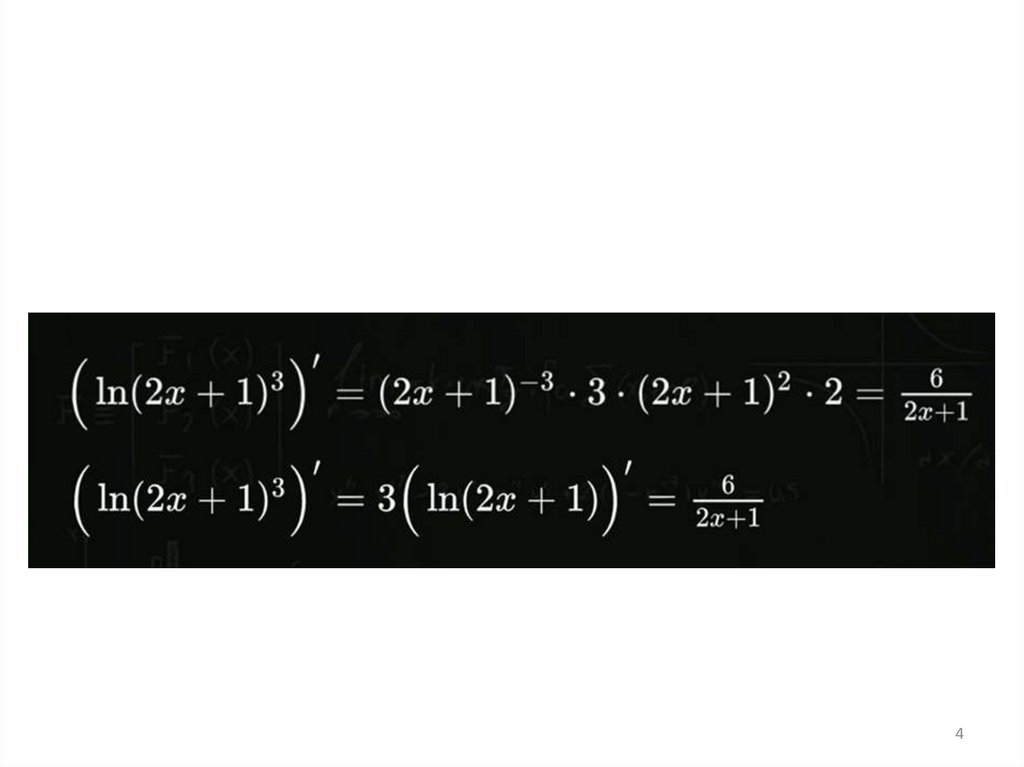






















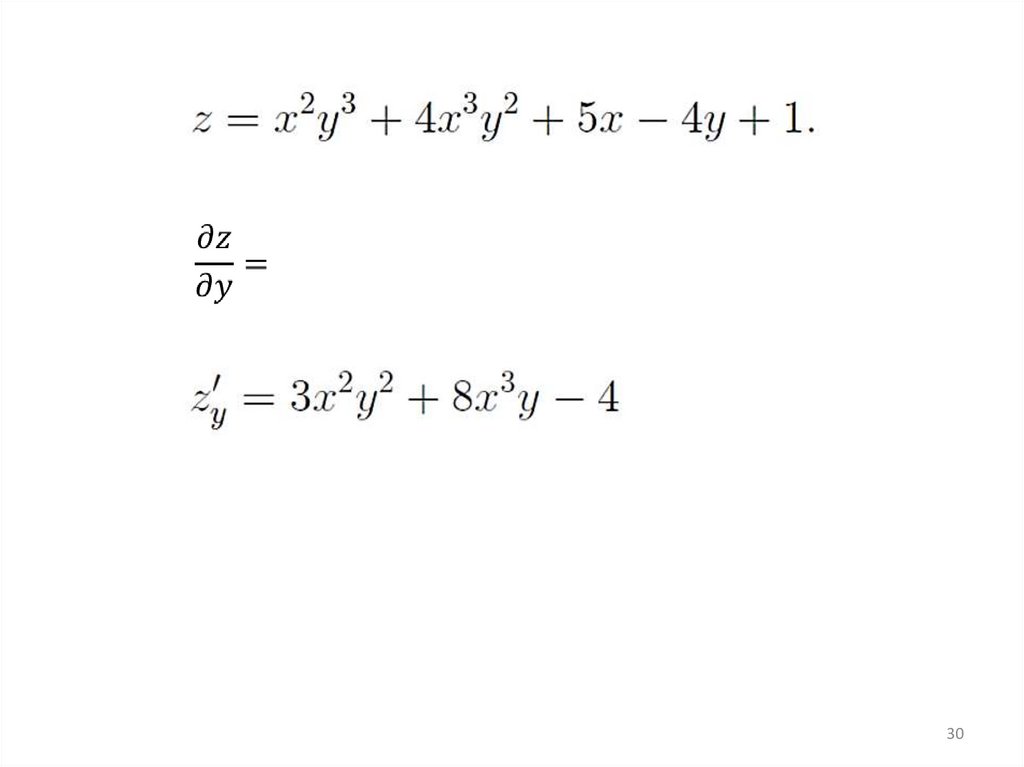





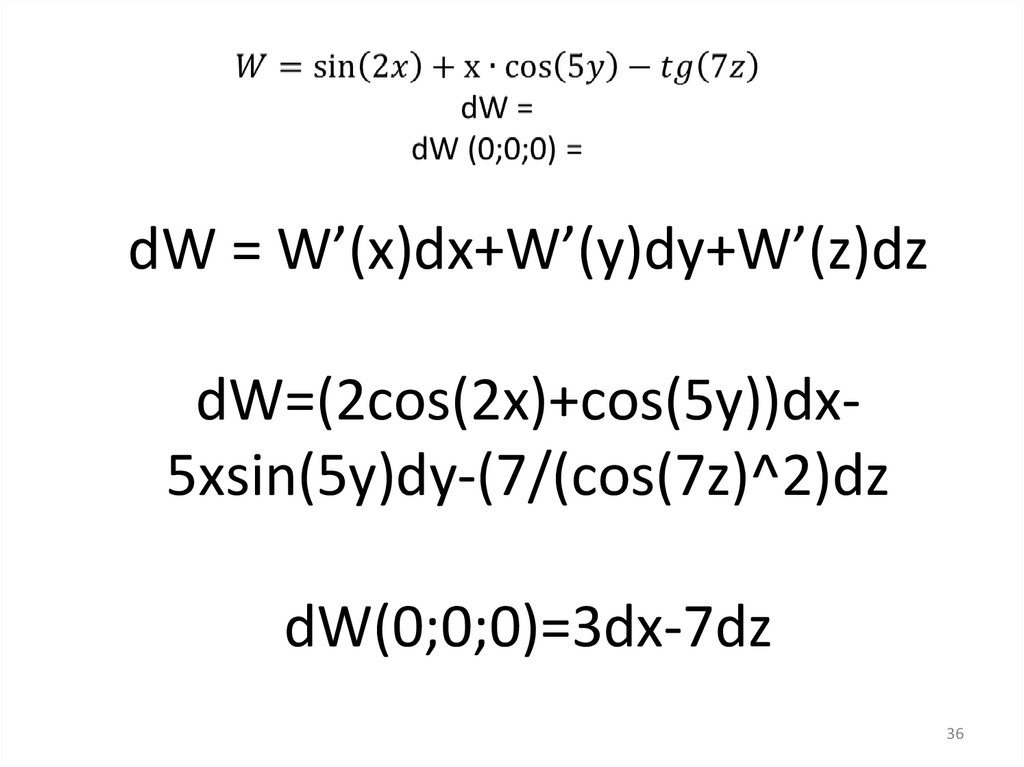




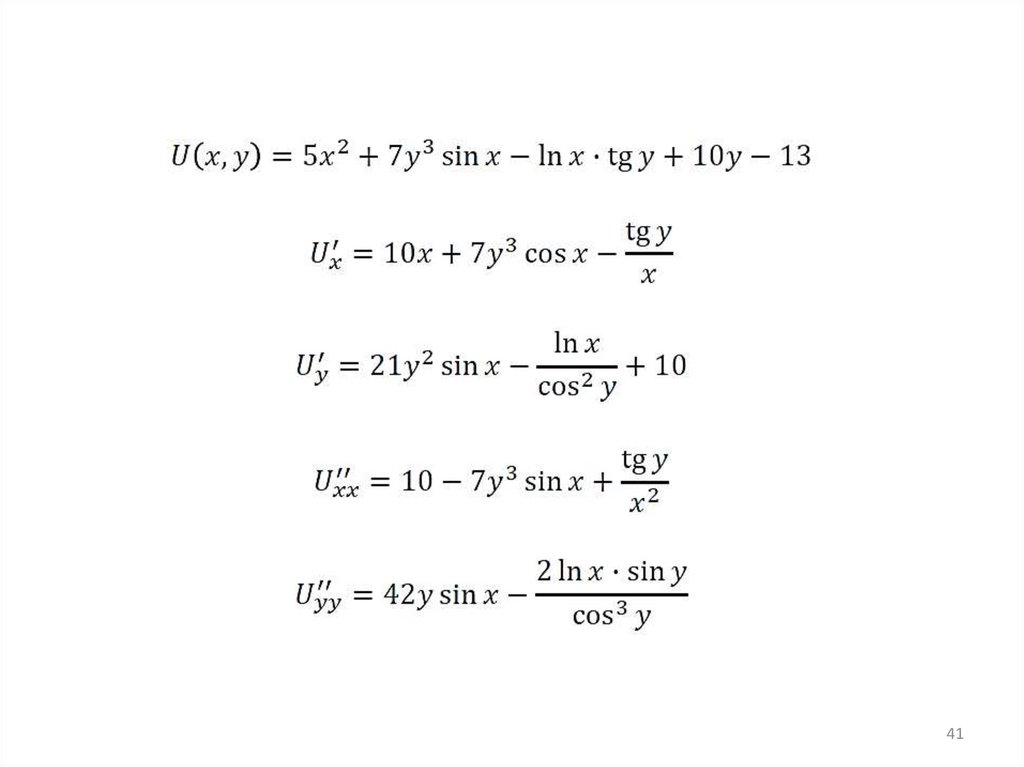
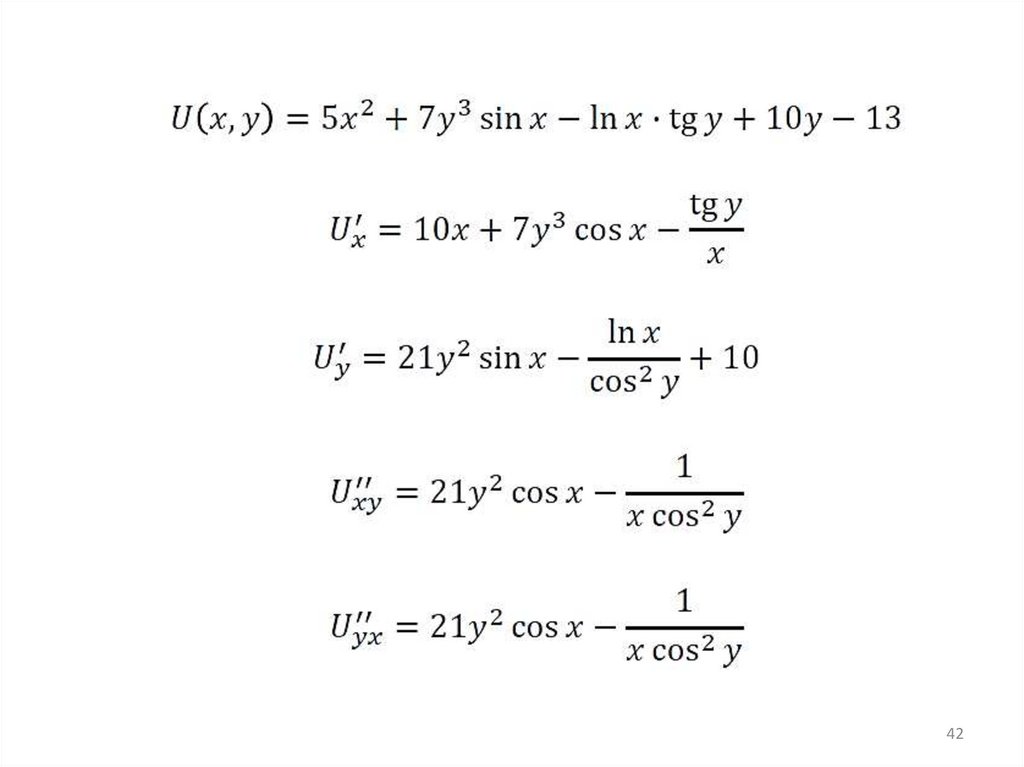
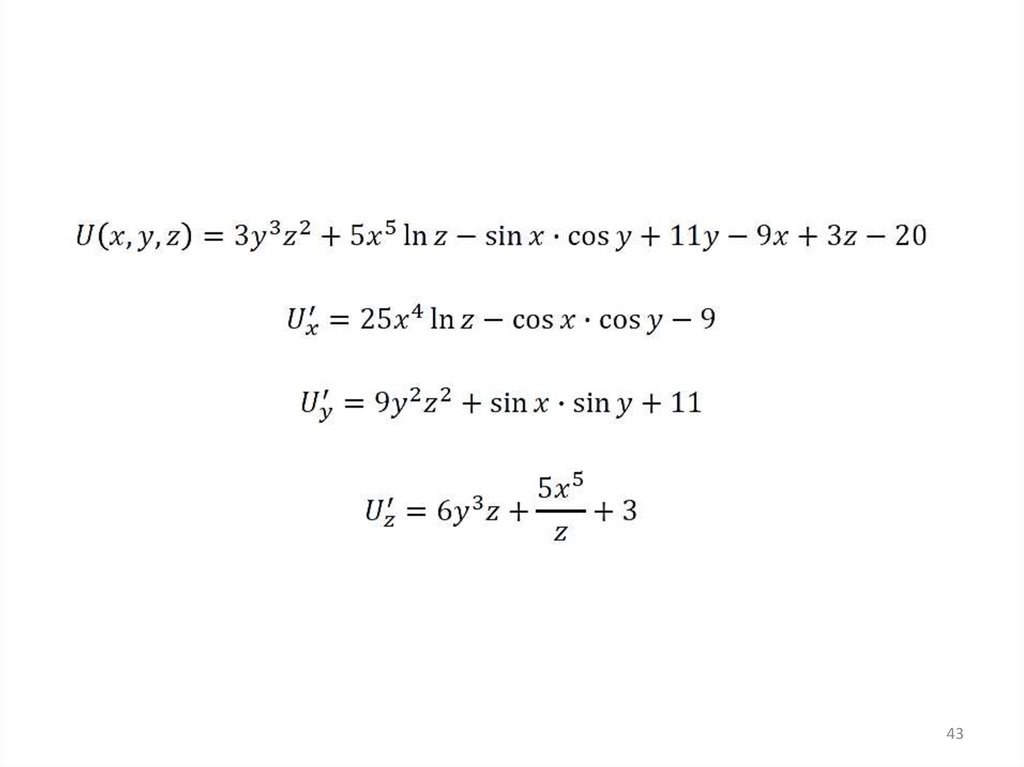
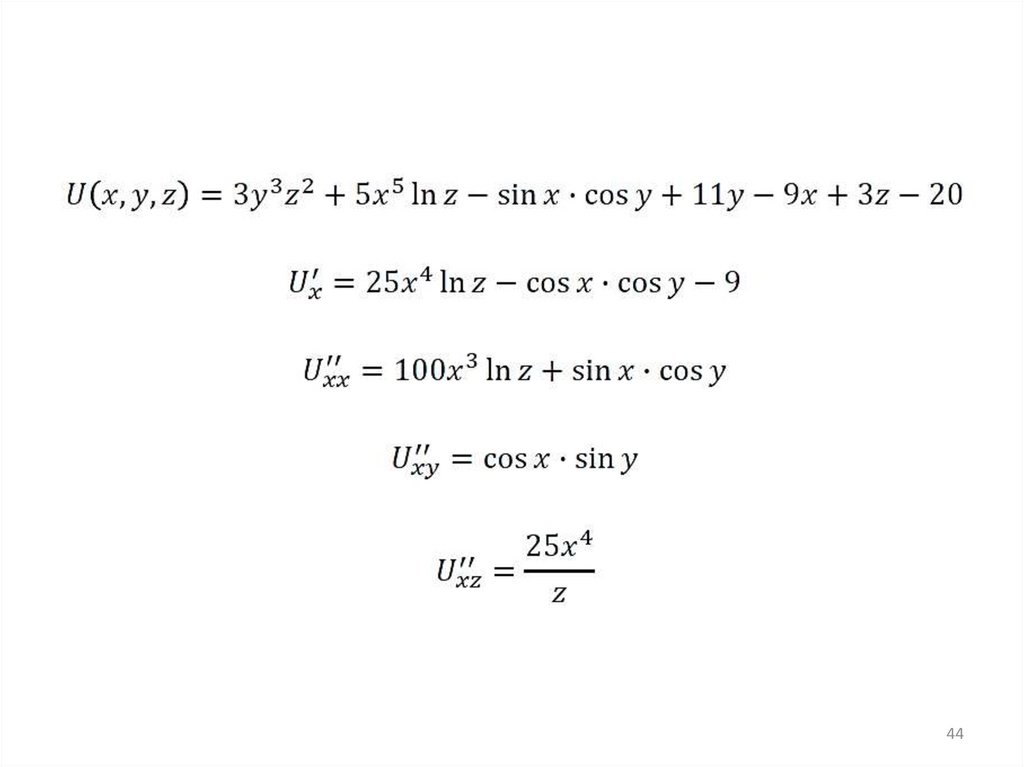
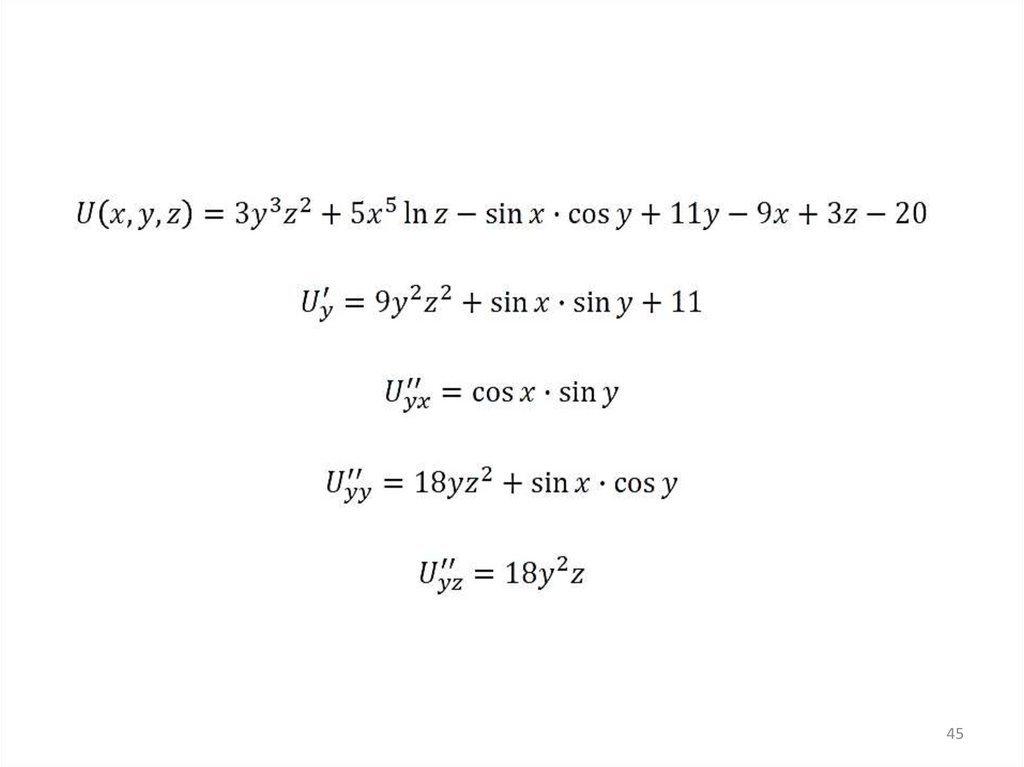




















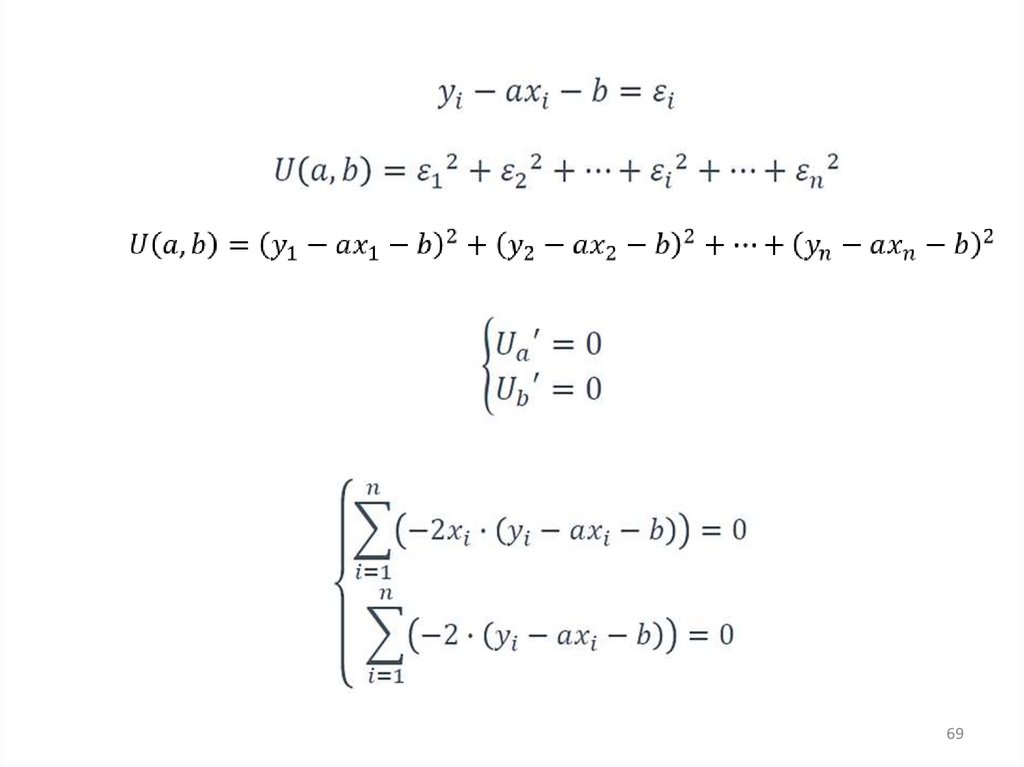






 mathematics
mathematics








