Similar presentations:
Производные функции нескольких переменных (часть 1). Введение в математический анализ
1.
Производные функциинескольких переменных
(часть 1)
Введение в математический анализ
2.
План0.1) Разберём ДЗ.
1. Несколько слов о математическом
моделировании.
2. Функции 2-х переменных; функции многих
переменных.
3. Частные производные, дифференциалы функций.
4. Экстремум функции 2-х переменных.
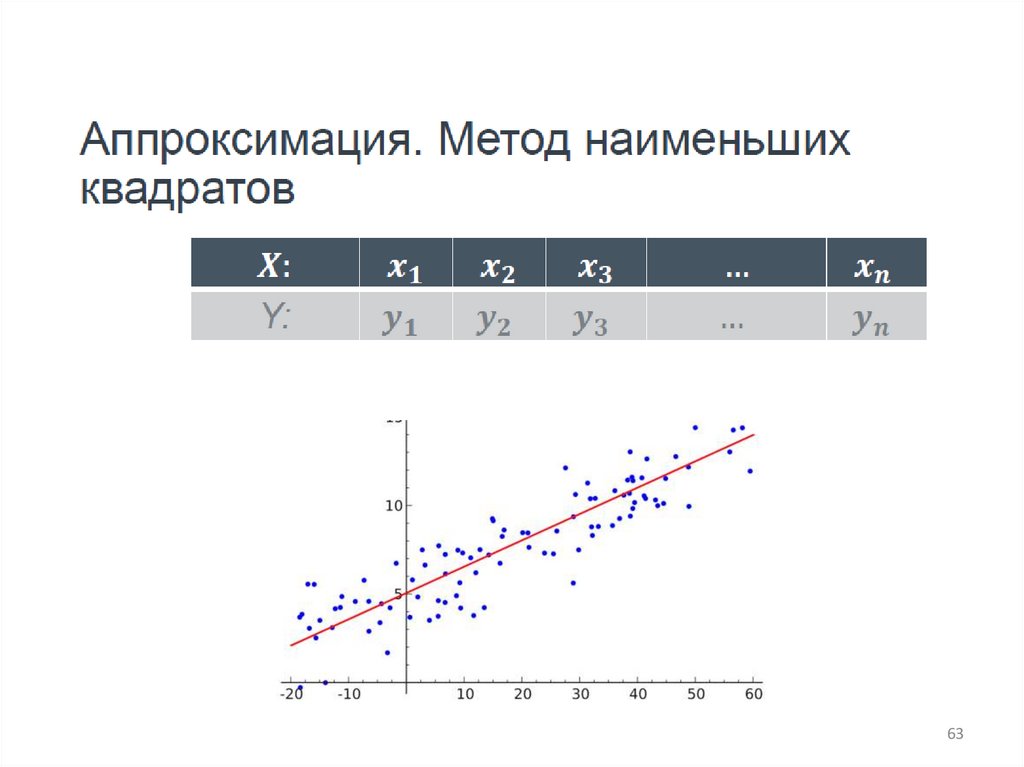
5. Аппроксимация. МНК.
2
3.
Разбор ДЗ по теме «Производныеодной переменной»
3
4.
45.
56.
67.
- (2pi^(1/2)+3)*sin(pi+3pi^(1/2)) = (2pi^(1/2)+3)*(sin(pi)cos(3pi^(1/2))+ cos(pi)sin(3pi^(1/2)))=- (2pi^(1/2)+3)*(0 - sin(3pi^(1/2)))=
(2pi^(1/2)+3)*sin(3pi^(1/2)) = -5,38 (с округлением).
7
8.
Задание 68
9.
910.
1011.
Функции многих переменных.Где применяется математическое
моделирование?
модели потребительского выбора, фирмы
(производственные функции);
экономического роста; равновесия на
товарных, факторных и финансовых рынках и
т. д.
11
12.
Математическое моделирование –зачем?
• Упрощённо описать реальность.
• Учесть ключевые факторы.
• Принять решение.
• Математическая модель – основа для
принятия решения.
12
13.
Задачи математическогопрограммирования
Решают: проблему выбора, оптимизации.
У истоков: Канторович, Кун, Таккер.
13
14.
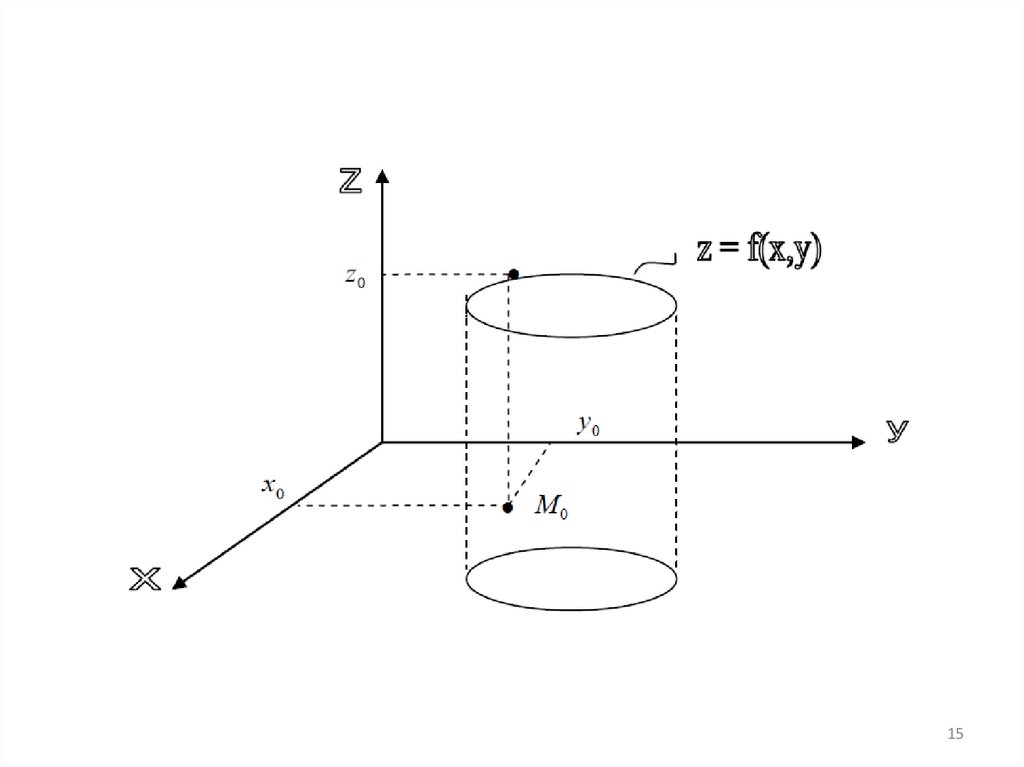
Функция 2-х переменных:определение.
График функции - поверхность
14
15.
1516.
Область определения функции 2-хпеременных D(x;y)
16
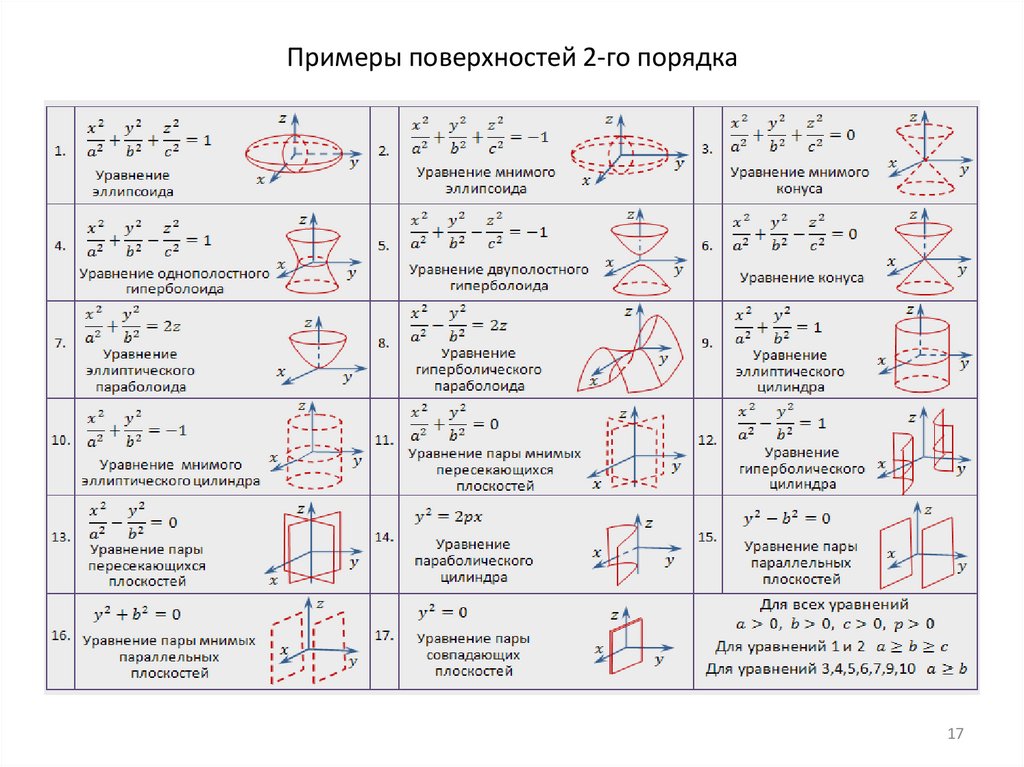
17.
Примеры поверхностей 2-го порядка17
18.
Пример18
19.
Пример19
20.
ПримерD(x;y)
Круг радиуса 1 в центре с началом координат
20
21.
Функция многих переменных:определение.
21
22.
Частные производные 1-го порядка- «дельта икс», приращение переменной x
=
22
23.
Определениепроизводной функции
одной переменной
(для сравнения)
23
24.
Вычисление частных производных24
25.
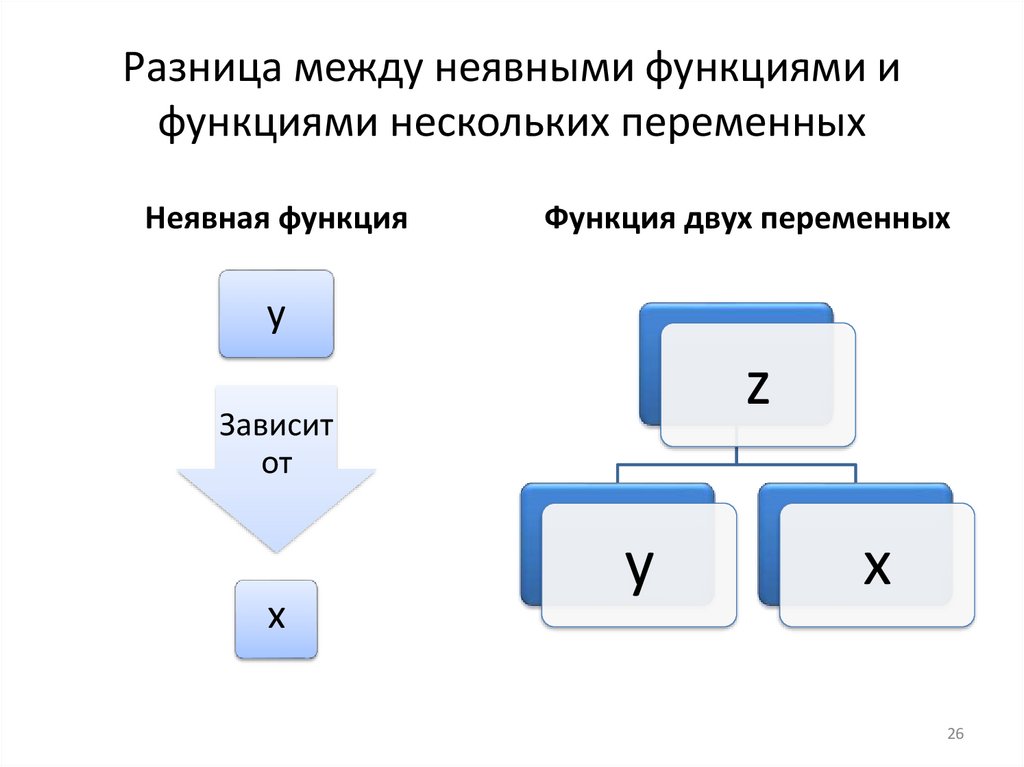
Сравнение с неявными функциямиВ случае неявной функции y зависит от х: y(x)
В случае функции нескольких переменных – нет: z(x,y)
25
26.
Разница между неявными функциями ифункциями нескольких переменных
Неявная функция
Функция двух переменных
у
z
Зависит
от
y
x
26
х
27.
Вычислить:27



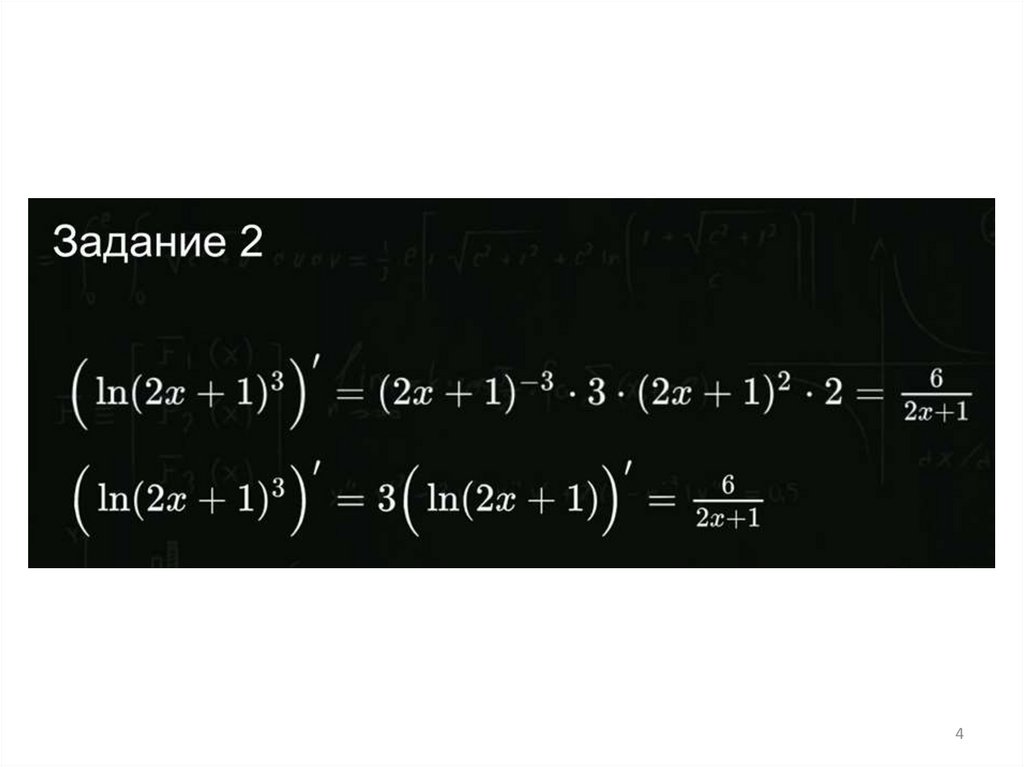





















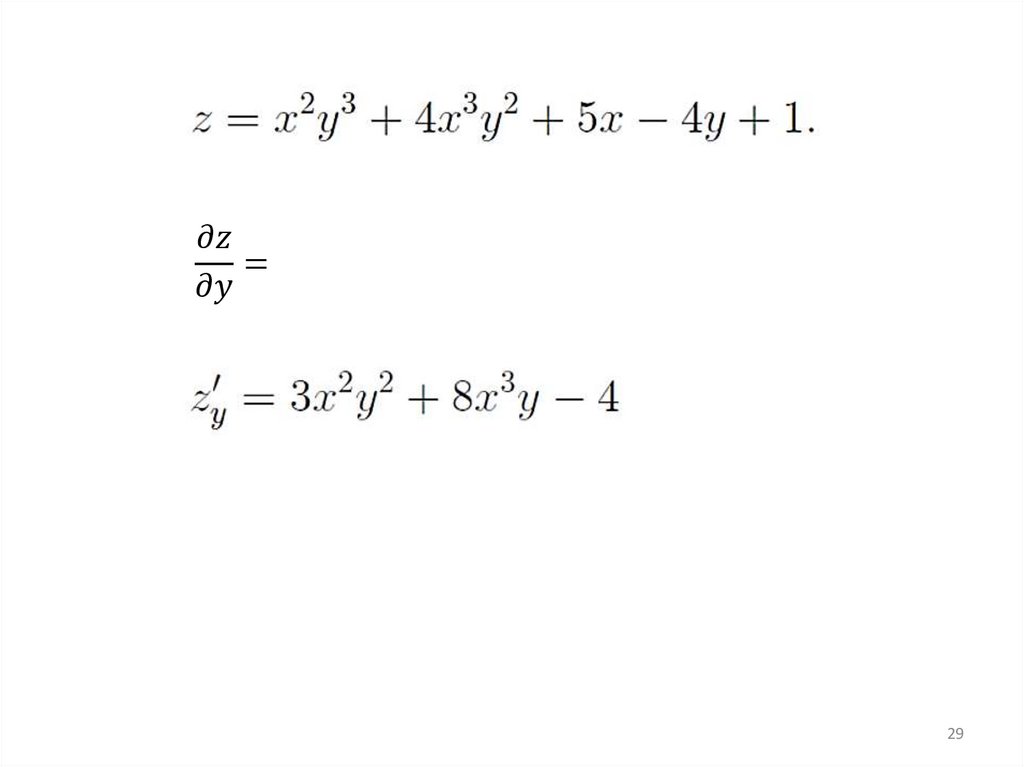









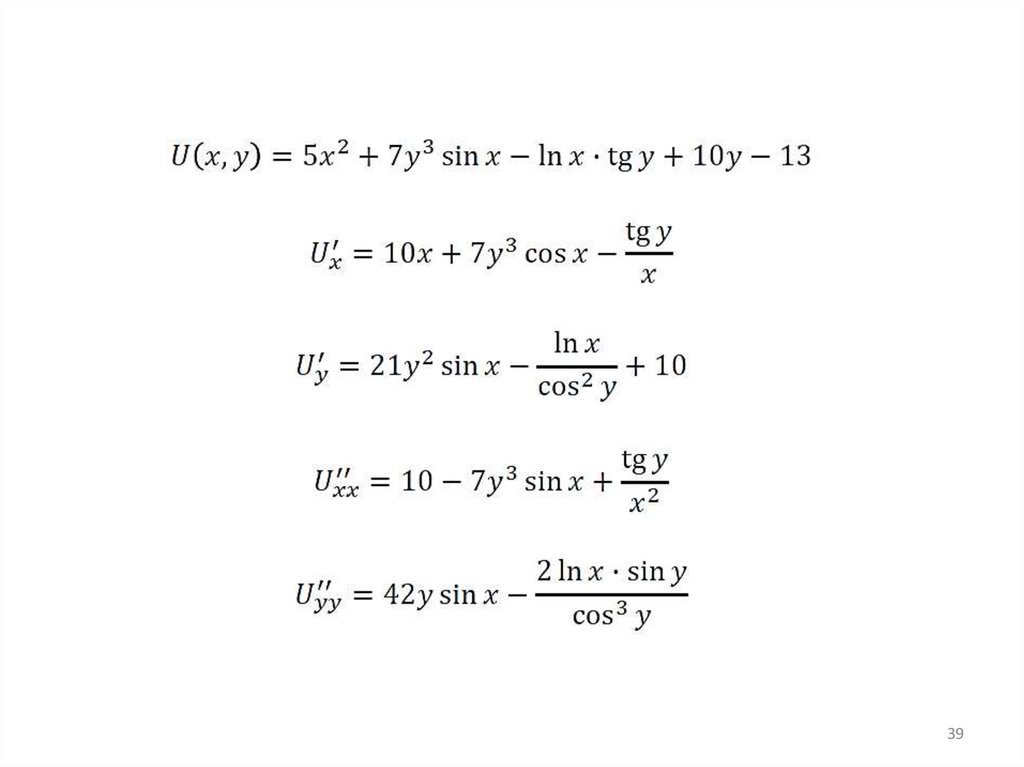
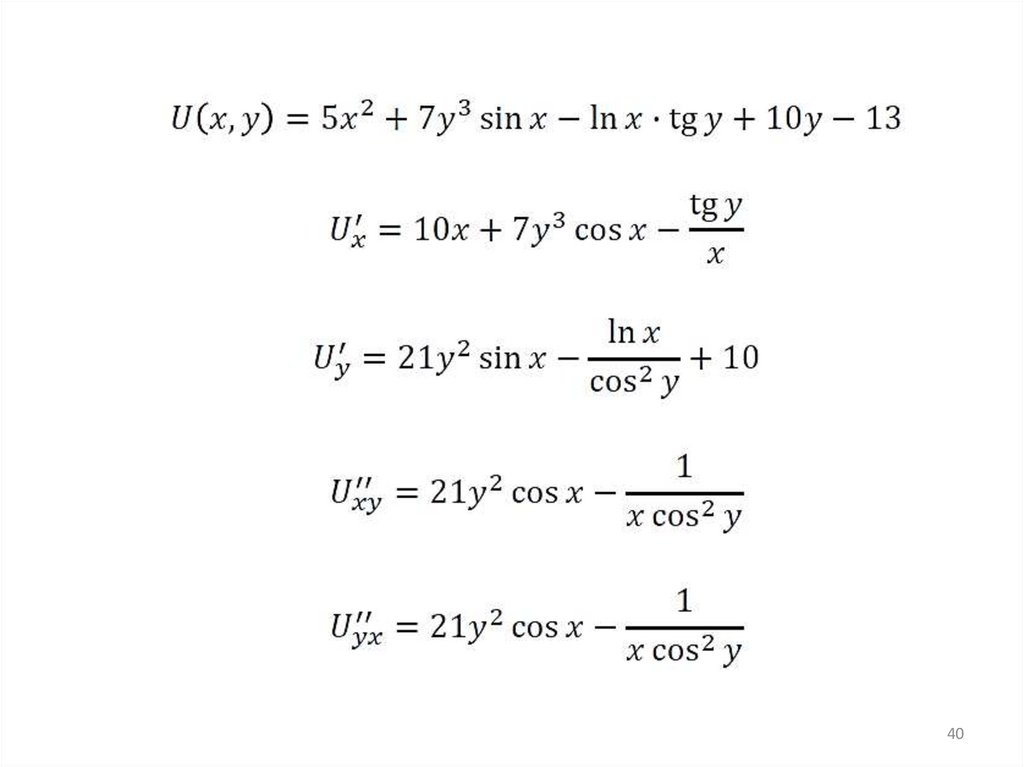
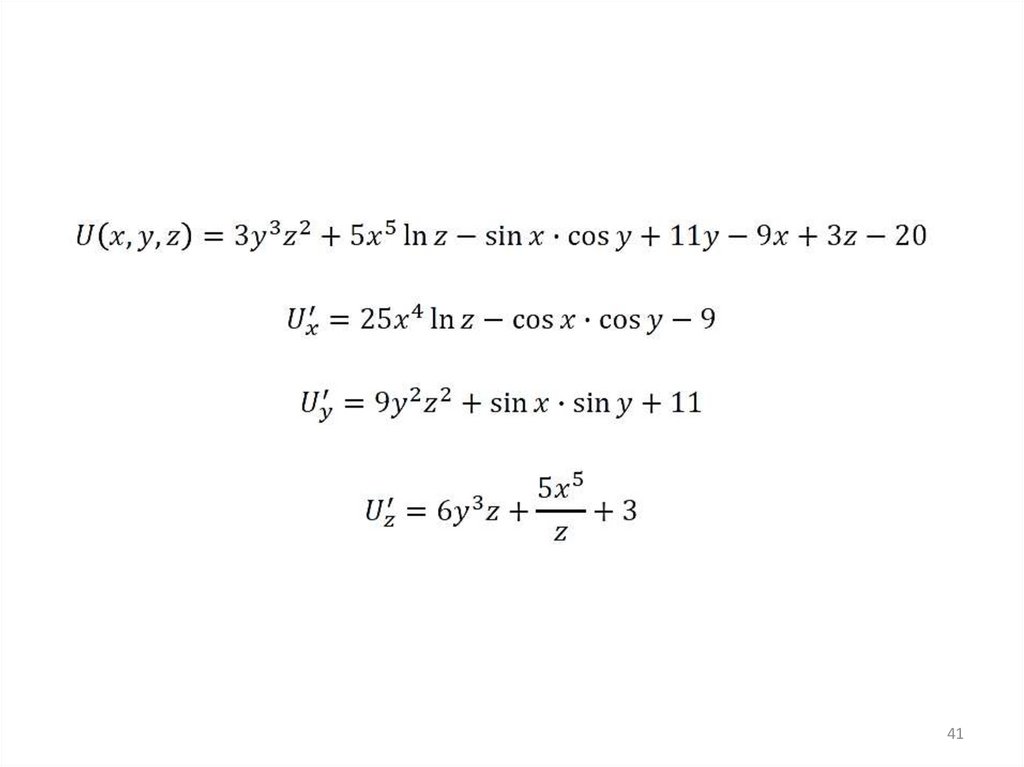
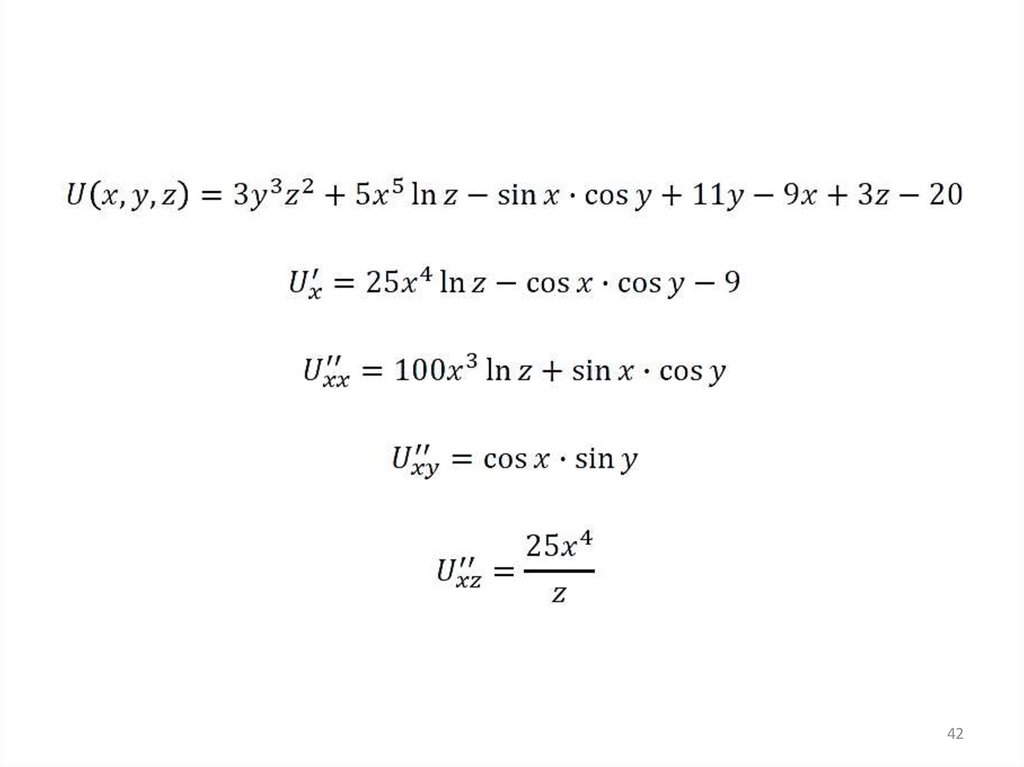
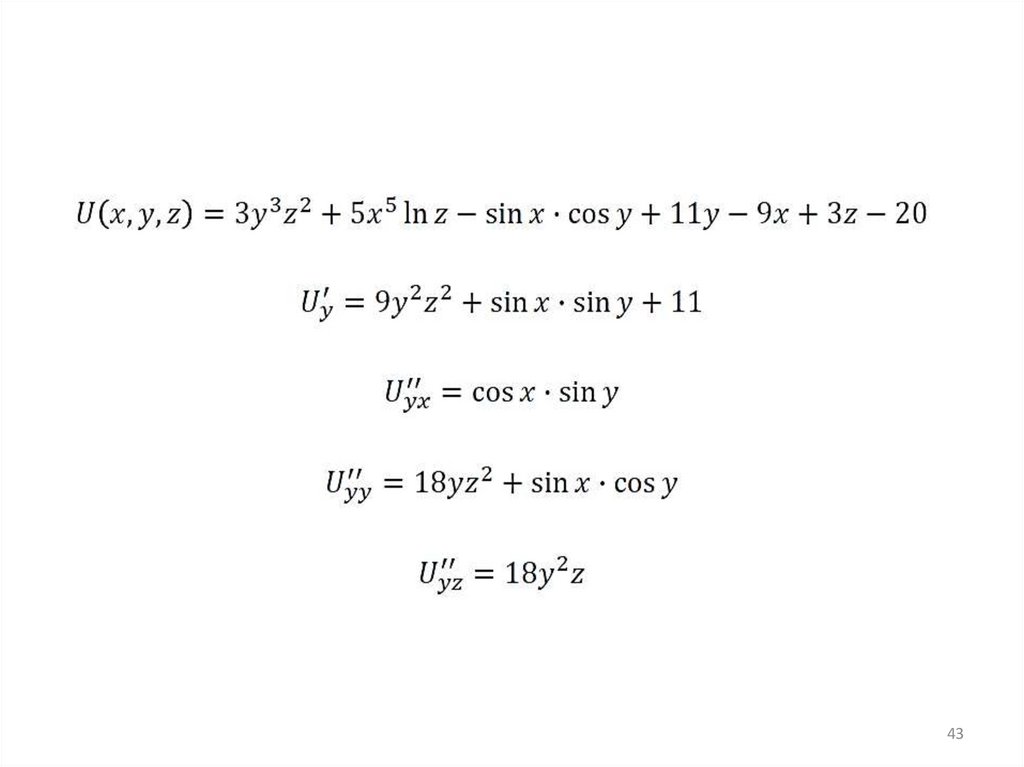
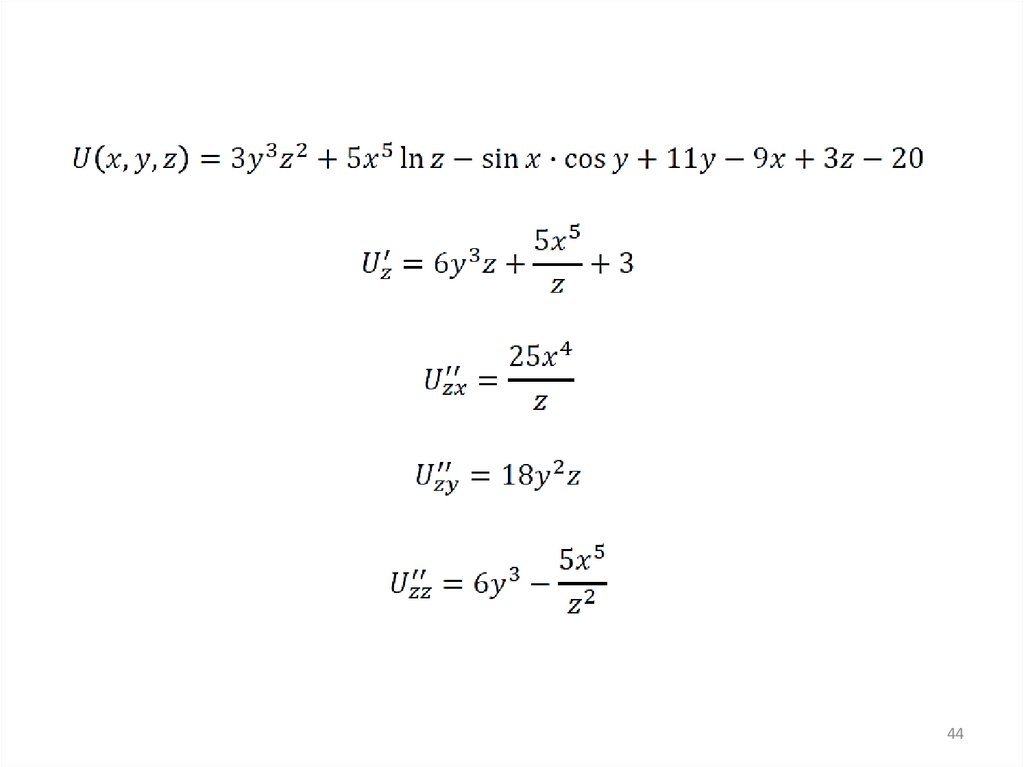



















 mathematics
mathematics








