Сложное (составное) движение точки

1.

Сложное (составное) движение точки
Сложное движение точки
Сложное (составное) движение точки - такое
движение, которое может быть составлено из двух
(нескольких) простых движений.
Движение рассматривается
координат:
неподвижной
(движущейся).
в
двух системах
и
подвижной

2. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ

движение, которое допускает разделение на два
простых с помощью дополнительной подвижной
системы отсчета
Сложное движение

3.

Сложное движение точки
Хʹ У ʹ Z ʹ - неподвижная система координат - НПСК
Х У Z – подвижная система координат - ПСК
м
z
z'
o'
x'
o
x
y'
y
Подвижная точка М

4.

Сложное движение точки
Движение точки относительно неподвижной
системы координат называется абсолютным.
Движение точки относительно подвижной
системы
координат
называется
относительным.
Движение
подвижной
системы
координат
относительно неподвижной системы координат
называется переносным.

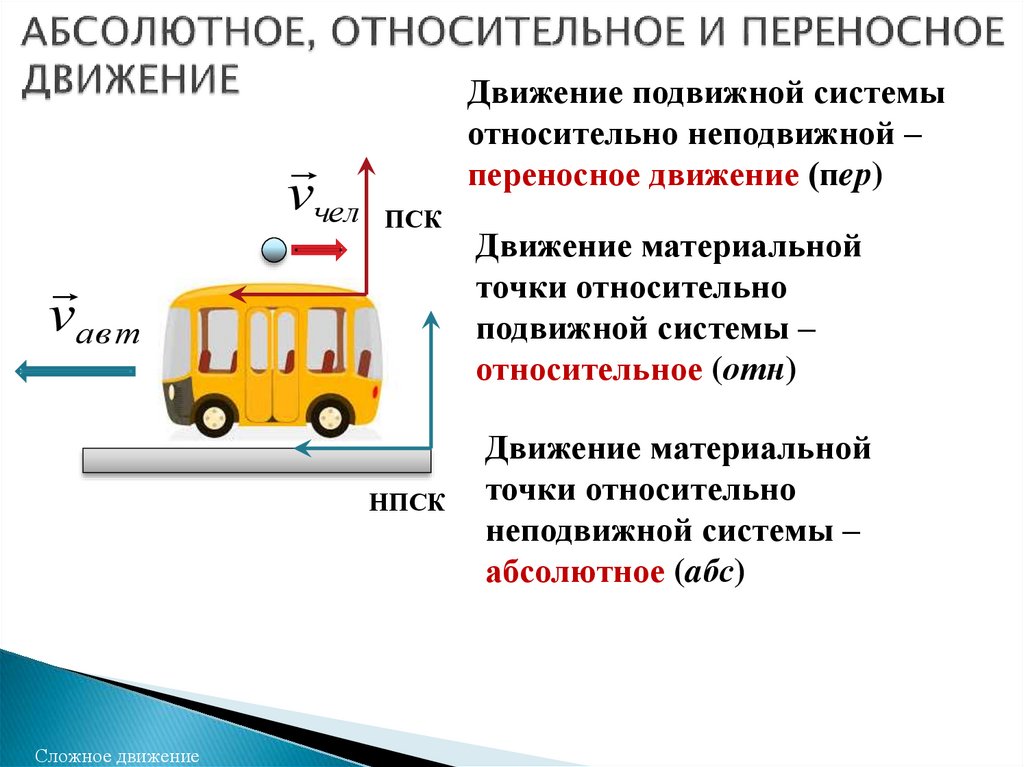
5. АБСОЛЮТНОЕ, ОТНОСИТЕЛЬНОЕ И ПЕРЕНОСНОЕ ДВИЖЕНИЕ

vчел
Движение подвижной системы
относительно неподвижной –
переносное движение (пeр)
ПСК
vав т
НПСК
Сложное движение
Движение материальной
точки относительно
подвижной системы –
относительное (отн)
Движение материальной
точки относительно
неподвижной системы –
абсолютное (aбс)

6. Теорема о сложении скоростей:

Сложное движение точки
Теорема о сложении скоростей:
V Vотн Vпер
Абсолютная скорость точки равна геометрической
сумме переносной и относительной скоростей

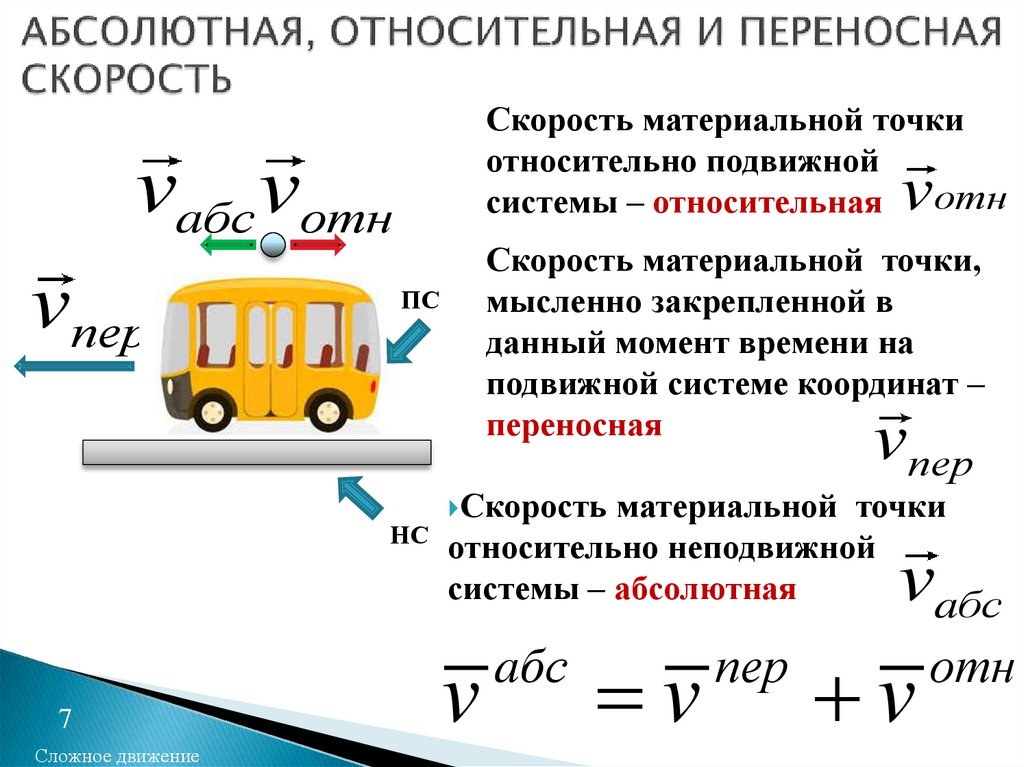
7. АБСОЛЮТНАЯ, ОТНОСИТЕЛЬНАЯ И ПЕРЕНОСНАЯ СКОРОСТЬ

Скорость материальной точки
относительно подвижной
системы – относительная отн
vaбс vотн
vпeр
v
Скорость материальной точки,
мысленно закрепленной в
данный момент времени на
подвижной системе координат –
переносная
ПС
vпeр
НС
Скорость
материальной точки
относительно неподвижной
системы – абсолютная
vaбс
7
Сложное движение
v
aбс
v
пер
v
отн

8.

Сложное движение точки
Скорости и ускорения при сложном движении
обозначаются
Vабс,
aабс- абсолютные
Vотн ,
Vпeр ,
- относительные
aотн
- переносные
aпeр
Сложение векторов скорости по теореме косинусов
Vaбс
Vпeр
Vотн
Vaбс Vотн Vпeр
2
2
Vaбс Vотн
Vпeр
2VотнVпeр cos

9.

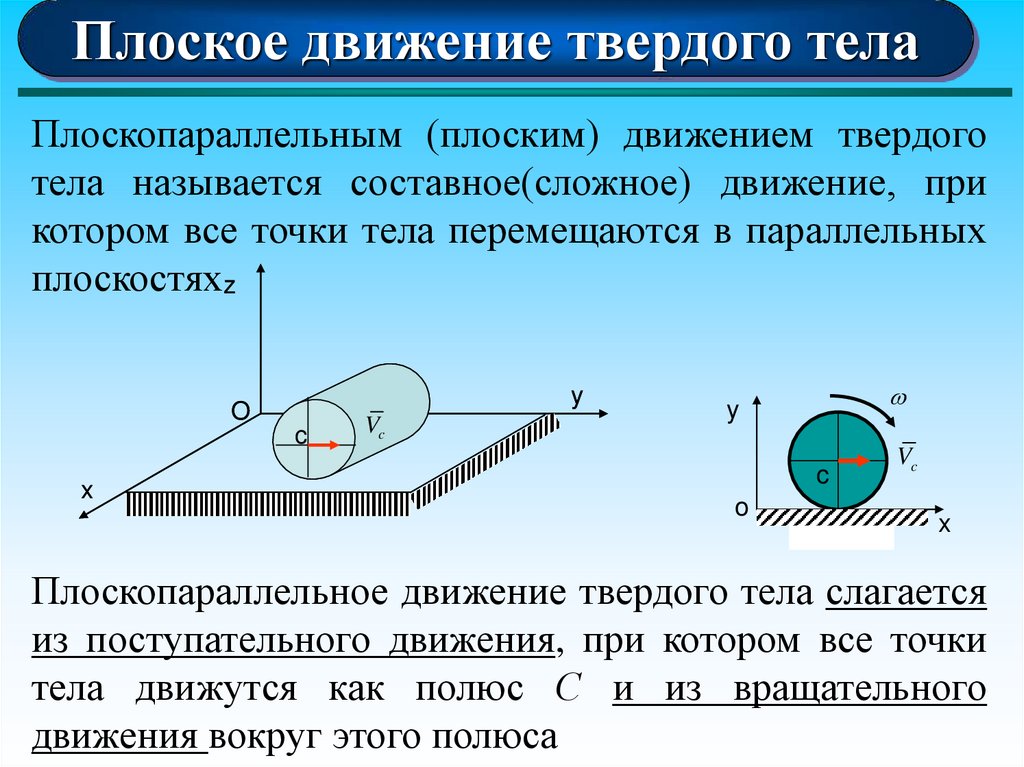
Плоское движение твердого тела
Плоскопараллельным (плоским) движением твердого
тела называется составное(сложное) движение, при
котором все точки тела перемещаются в параллельных
плоскостяхz
y
O
c
x
Vc
y
c
c
o
Рис.3.
Vc
x
Плоскопараллельное движение твердого тела слагается
из поступательного движения, при котором все точки
тела движутся как полюс С и из вращательного
движения вокруг этого полюса

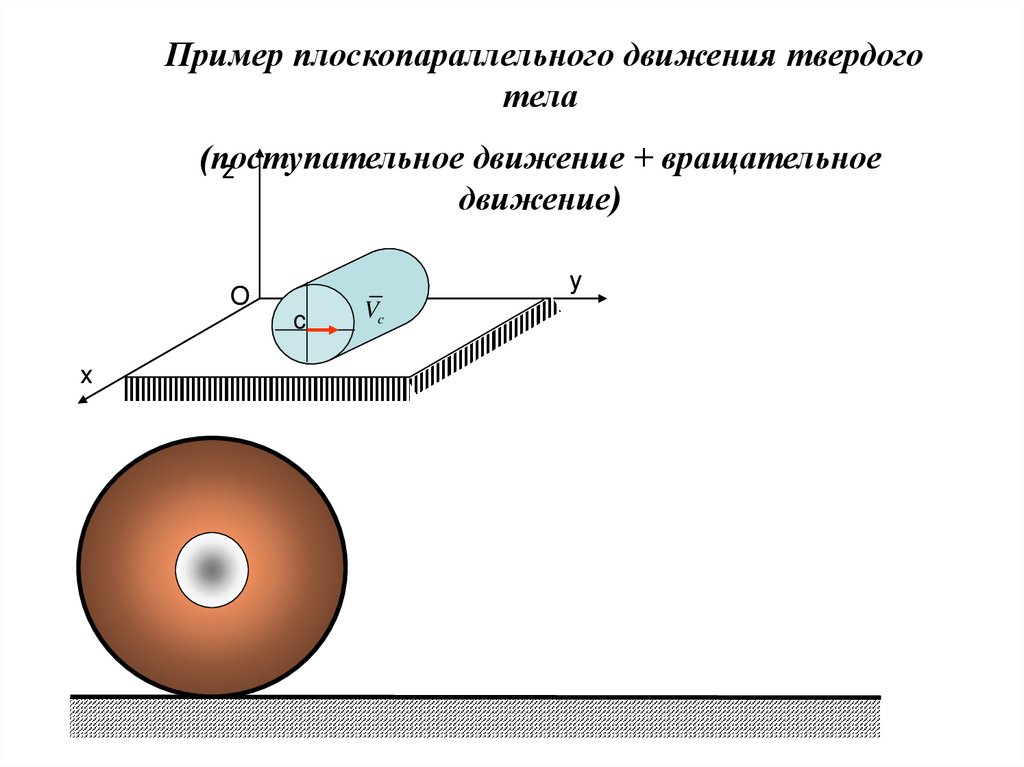
10.

Пример плоскопараллельного движения твердого
тела
(поступательное
движение + вращательное
z
движение)
y
O
c
x
Vc

11. Геометрическая интерпретация теоремы

Теорема о скоростях точек тела при плоскопараллельном
движении (ВЕКТОРНАЯ)
Геометрическая
Скорость произвольной точки
интерпретация теоремы
плоской фигуры равна
геометрической сумме скорости
полюса и вращательной скорости
этой точки вокруг оси, проходящей
через полюс (полюс это точка,
VBA
В-произвольная
точка
скорость которой известна).
VA
VB VA VBA
VB
VBA AB
ω
VBA AB
тела
тело
А-полюс
VA известная
скорость

12.

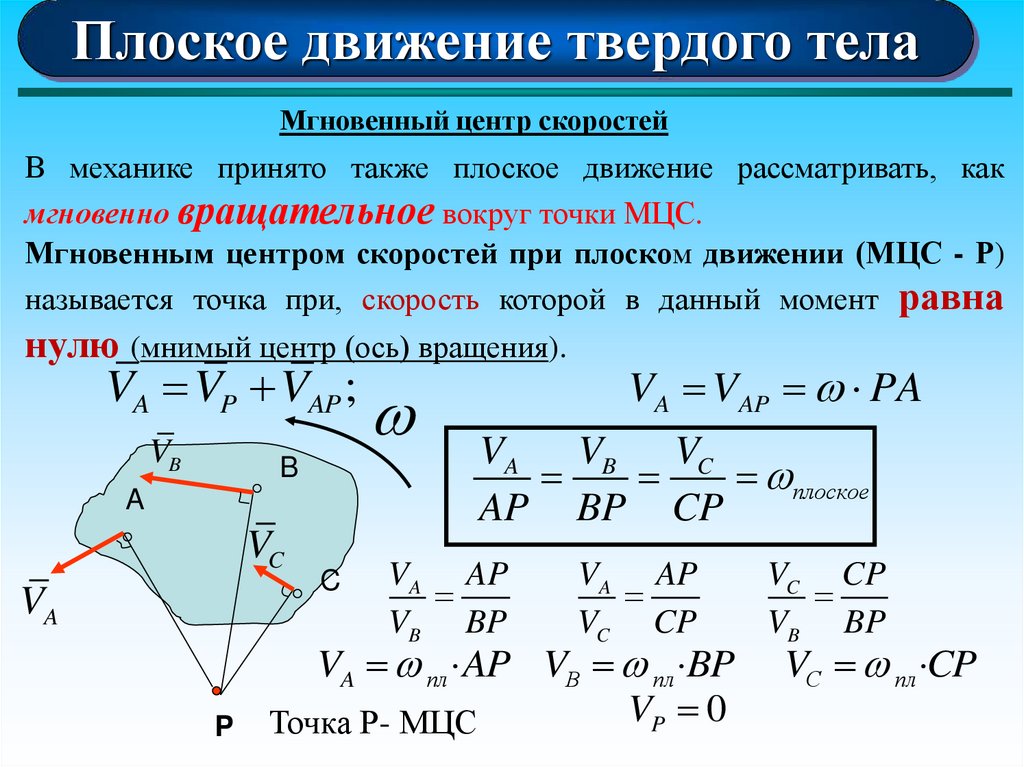
Плоское движение твердого тела
Мгновенный центр скоростей
В механике принято также плоское движение рассматривать, как
мгновенно вращательное вокруг точки МЦС.
Мгновенным центром скоростей при плоском движении (МЦС - Р)
называется точка при, скорость которой в данный момент равна
нулю (мнимый центр (ось) вращения).
VA VP VAP ;
VB
B
A
VC
VA
P
C
VA VAP PA
VA VB VC
плоское
AP BP CP
VA AP
VB BP
VA AP
VC CP
VA пл AP VB пл BP
VP 0
Точка Р- МЦС
VC CP
VB BP
VC пл CP

13.

VA
B
Правило нахождения
Мгновенного центра скоростей
A
VB
P
Мгновенным центром скоростей (МЦС)
называется точка, скорость которой в
данный момент времени равна нулю.
(может не лежать на теле и постоянно
меняющая своё положение)
Точка P – мгновенный центр
скоростей. VP=0
!!! Точка P находится на пересечении перпендикуляров,
восстановленных к скоростям в точках «А» и «В»
Найдём точку P - МЦС
VA VP VAP
VB VP VBP
VAP AP
VBP BP

14.

Плоское движение твердого тела
Свойства МЦС:
•Скорости всех точек фигуры перпендикулярны отрезкам,
соединяющим эти точки с МЦС
•Модули скоростей пропорциональны расстояниям точек
до МЦС
•Угловая скорость тела равна в каждый данный момент
времени отношению скорости какой-нибудь точки к ее
расстоянию до МЦС

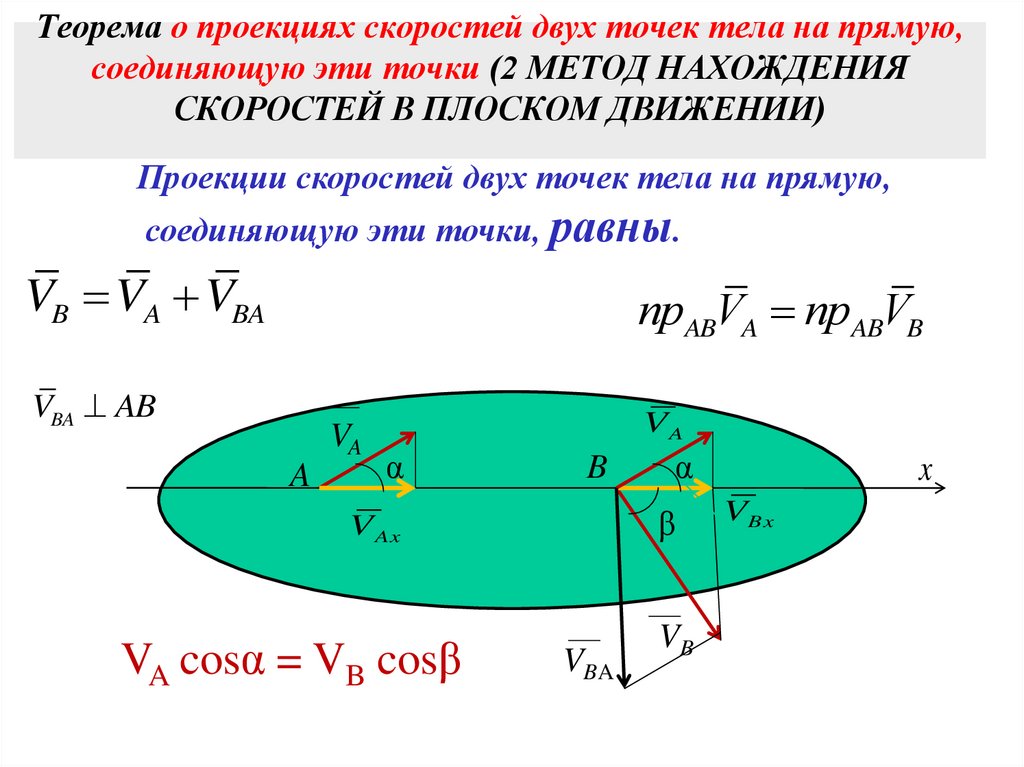
15. Теорема о проекциях скоростей двух точек тела на прямую, соединяющую эти точки (2 МЕТОД НАХОЖДЕНИЯ СКОРОСТЕЙ В ПЛОСКОМ

ДВИЖЕНИИ)
Проекции скоростей двух точек тела на прямую,
соединяющую эти точки, равны.
VB VA VBA
прABVA прABVB
VBA AB
VA
A
VA
α
B
β
V Ax
VA cosα = VB cosβ
α
VBA
VB
x
VBx

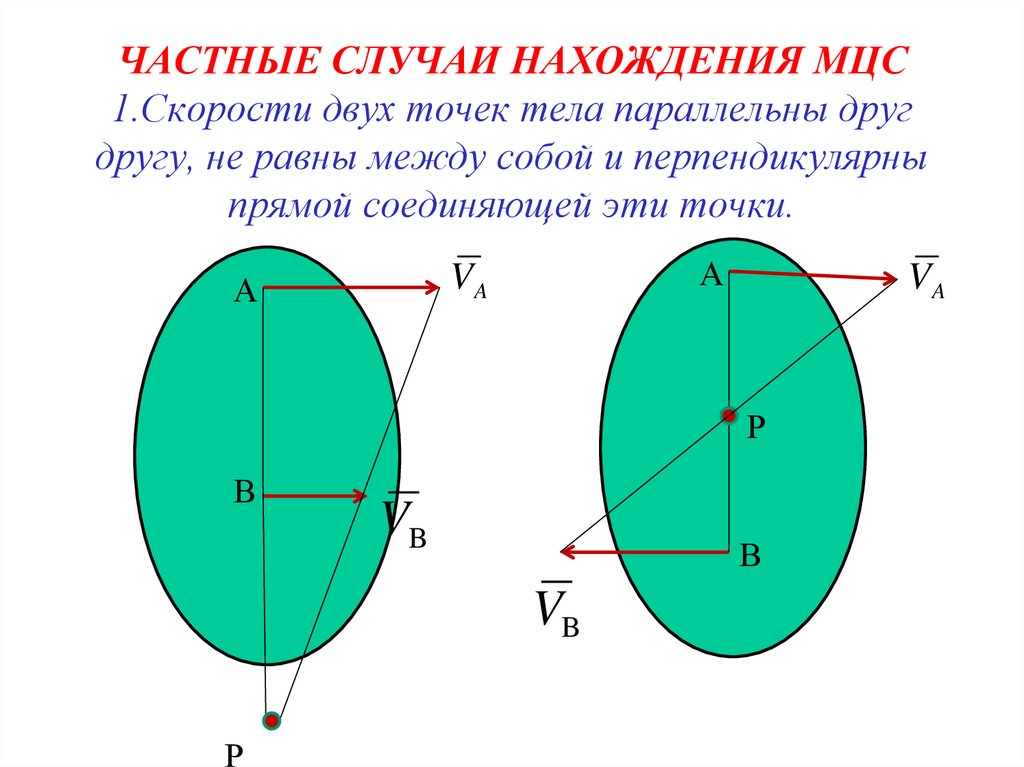
16. ЧАСТНЫЕ СЛУЧАИ НАХОЖДЕНИЯ МЦС 1.Скорости двух точек тела параллельны друг другу, не равны между собой и перпендикулярны прямой

соединяющей эти точки.
А
VA
А
VA
Р
В
VB
В
VB
Р

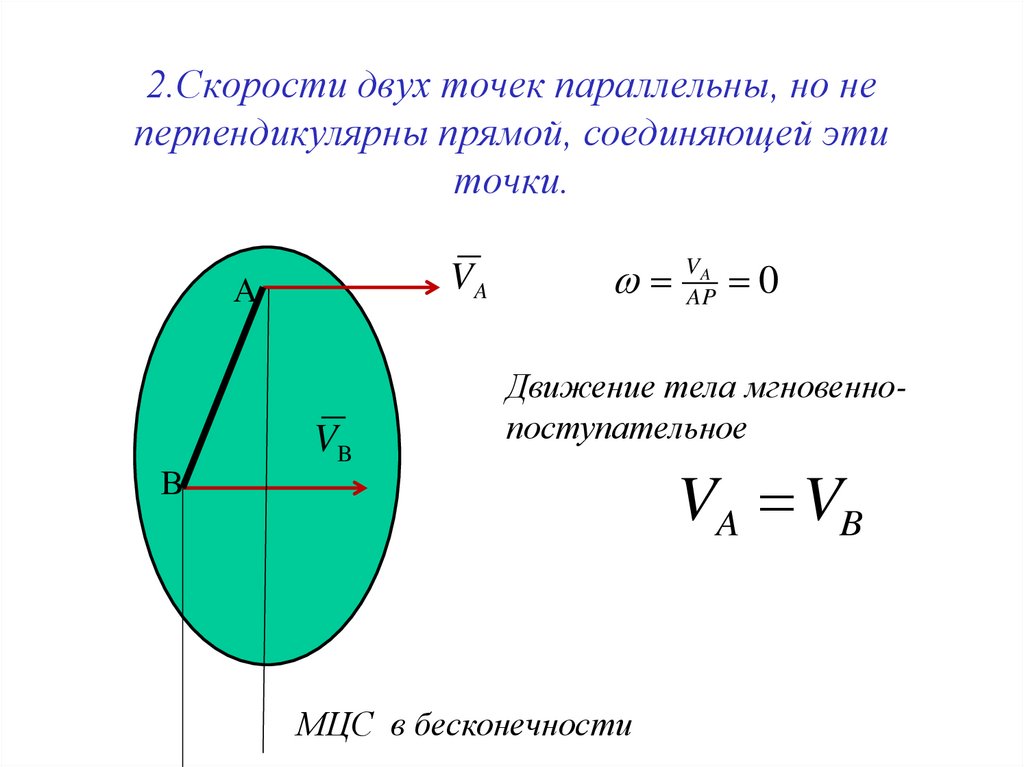
17. 2.Скорости двух точек параллельны, но не перпендикулярны прямой, соединяющей эти точки.

VA
А
В
VB
VA
AP
0
Движение тела мгновеннопоступательное
МЦС в бесконечности
VA VB

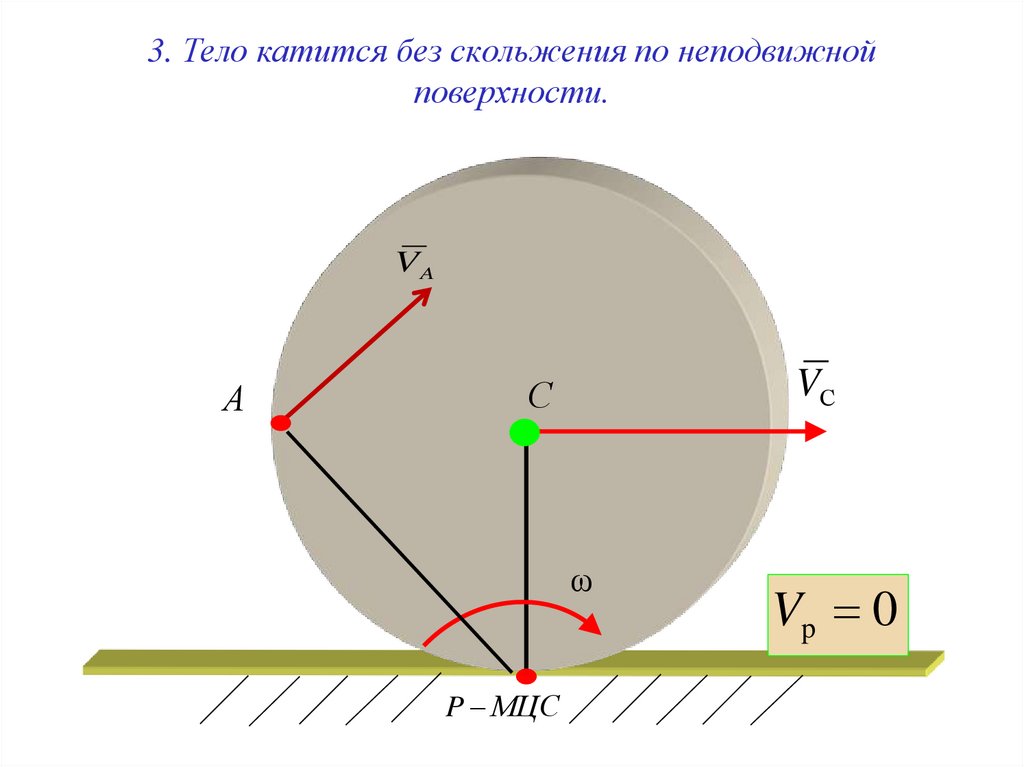
18. 3. Тело катится без скольжения по неподвижной поверхности.

VA
А
VС
С
ω
P МЦС
Vp 0

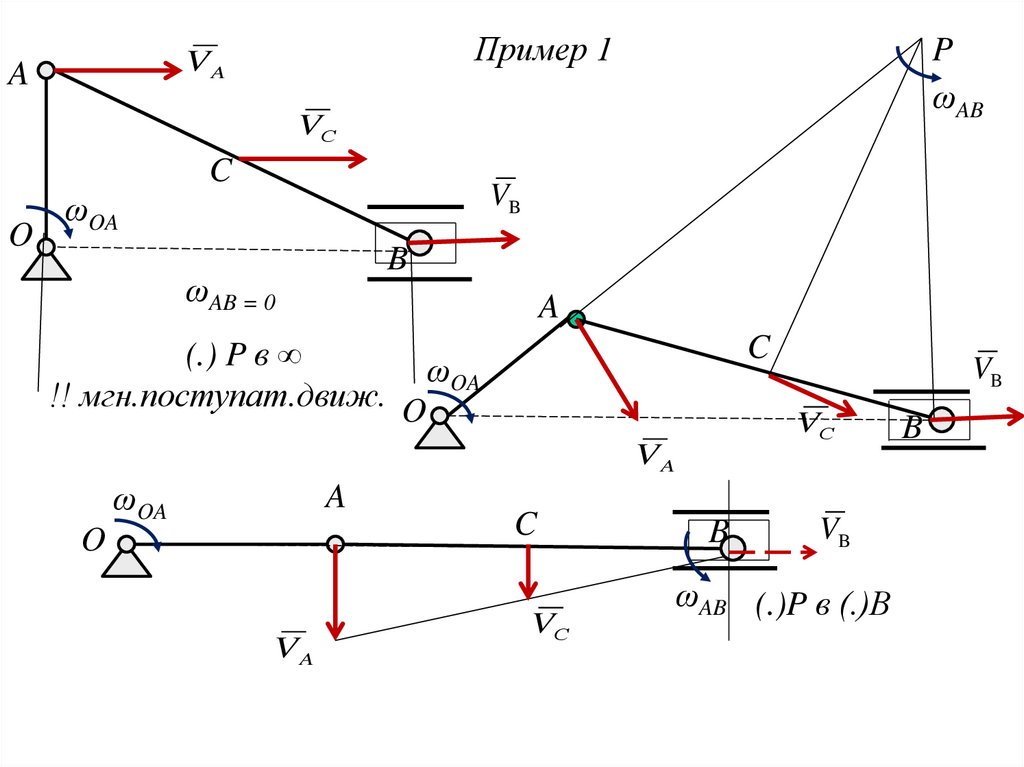
19.

Пример 1
VA
A
P
ωAB
VС
C
O
VB
ωOA
B
ωAB = 0
A
C
(.) P в ∞
ωOA
!! мгн.поступат.движ. O
VB
VС
VA
ωOA
A
O
VA
C
VС
B
VB
ωAB (.)P в (.)В
B

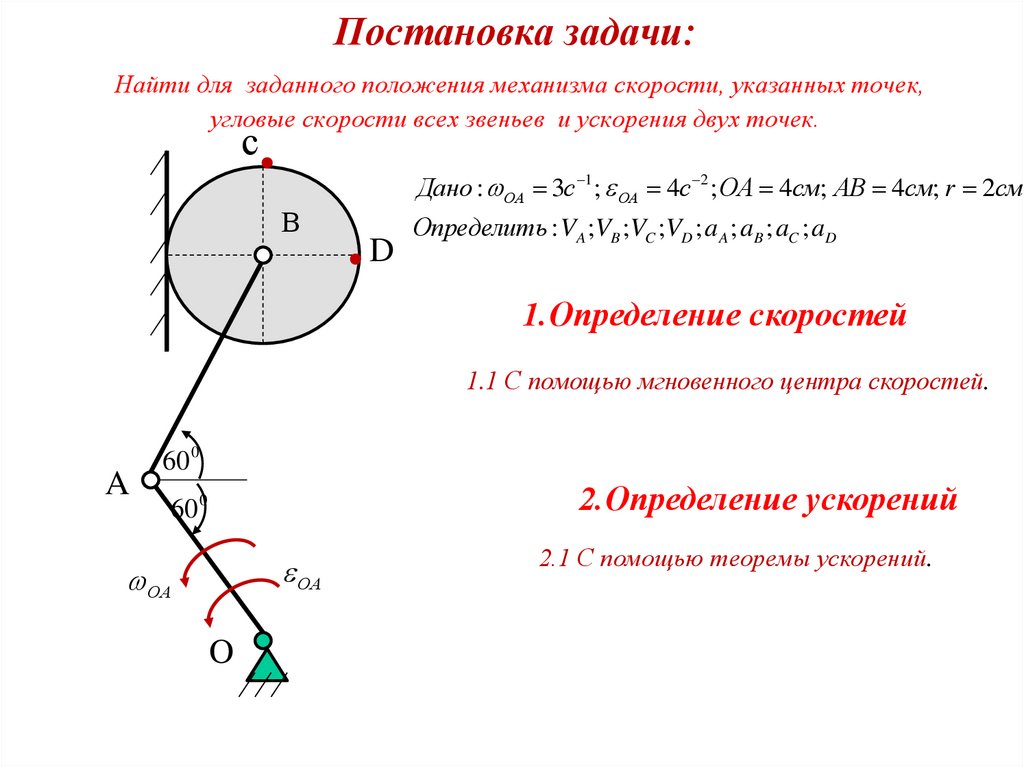
20. Постановка задачи: Найти для заданного положения механизма скорости, указанных точек, угловые скорости всех звеньев и ускорения

двух точек.
с
Дано : ОА 3с 1; ОА 4с 2 ; ОА 4см; АВ 4см; r 2см
ВВ
D
Определить : VA ;VB ;VC ;VD ; a A ; aB ; aC ; aD
1.Определение скоростей
1.1 С помощью мгновенного центра скоростей.
A
60 0
2.Определение ускорений
60 0
ОА
ОА
O
2.1 С помощью теоремы ускорений.

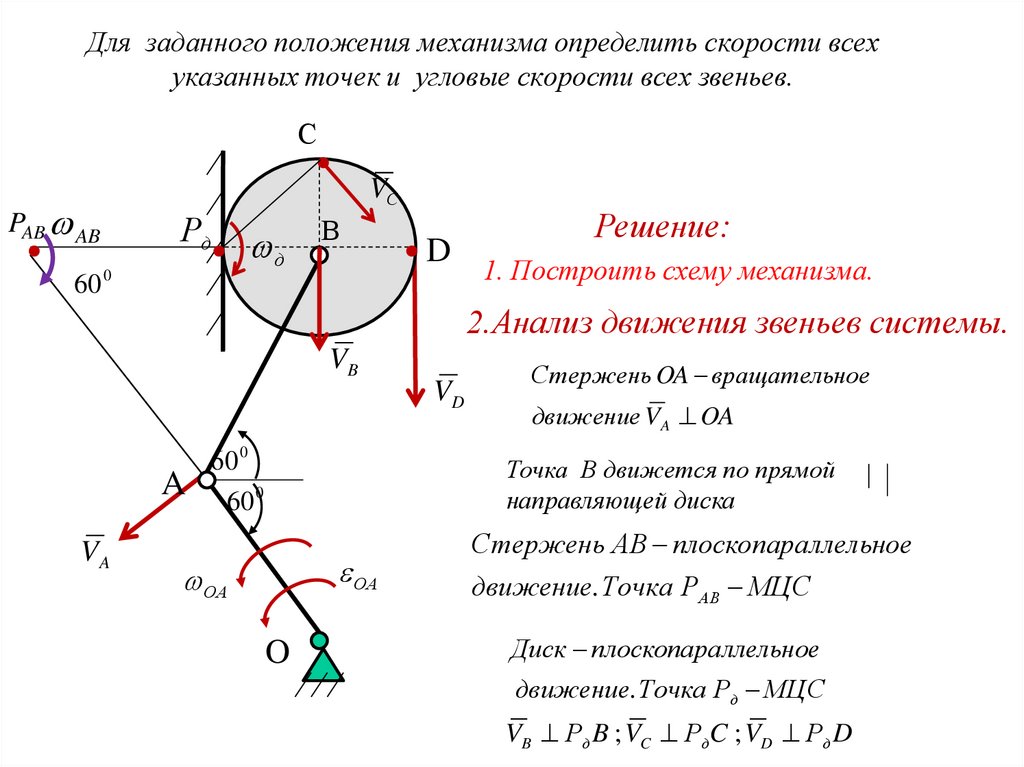
21. Для заданного положения механизма определить скорости всех указанных точек и угловые скорости всех звеньев.

С
VС
PAB AB
60
Рд
0
д
В
D
Решение:
1. Построить схему механизма.
2.Анализ движения звеньев системы.
VB
VD
A
VA
60 0
60 0
Стержень OA вращательное
движение VA OA
Точка В движется по прямой
направляющей диска
ОА
ОА
O
Стержень АВ плоскопараллельное
движение. Точка РАВ МЦС
Диск плоскопараллельное
движение. Точка Рд МЦС
VB Рд B ; VC РдC ; VD Рд D

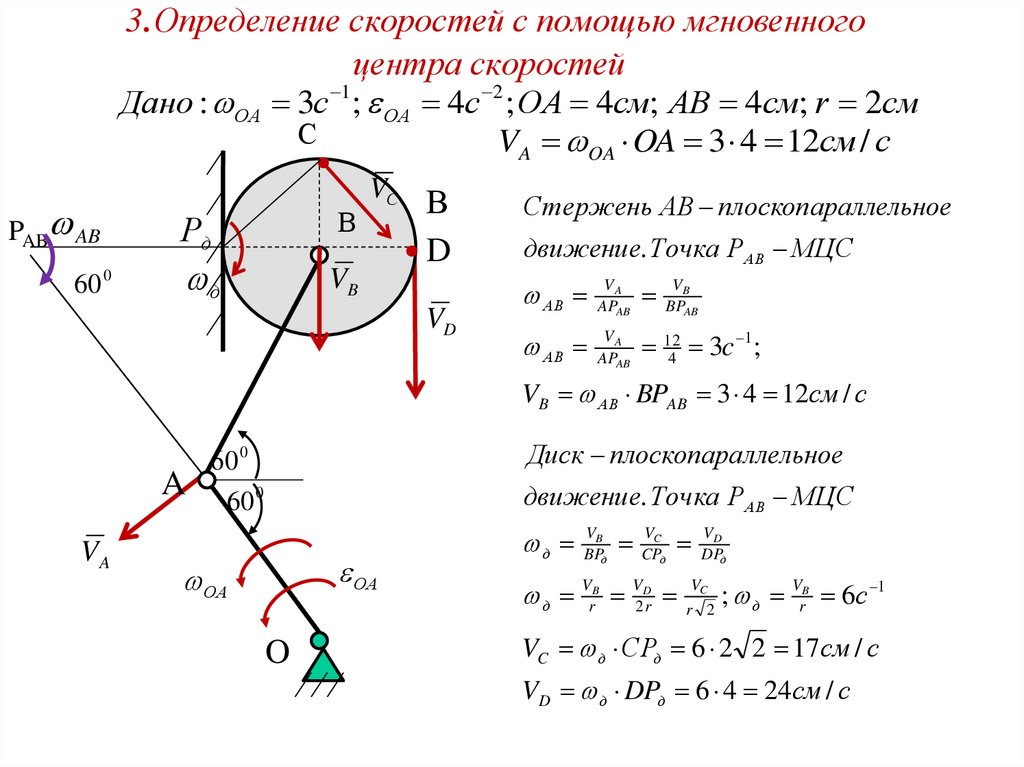
22. 3.Определение скоростей с помощью мгновенного центра скоростей

Дано : ОА 3с 1; OA 4с 2 ; ОА 4см; АВ 4см; r 2см
С
VA OA OA 3 4 12см / с
PAB AB
ВВ
Рд
д
60 0
VС
VB
В
D
VD
Стержень АВ плоскопараллельное
движение. Точка РАВ МЦС
АВ
VA
APAB
АВ
VA
APAB
124 3c 1 ;
VB
BPAB
VB АВ BPAB 3 4 12см / с
A
VA
Диск плоскопара ллельное
60 0
60 0
движение. Точка РАВ МЦС
ОА
ОА
O
д
VB
BPд
VС
CPд
д Vr V2 r
B
D
VD
DPд
VB
1
;
6
с
д
r
2
VC
r
VC д СPд 6 2 2 17см / с
VD д DPд 6 4 24см / с

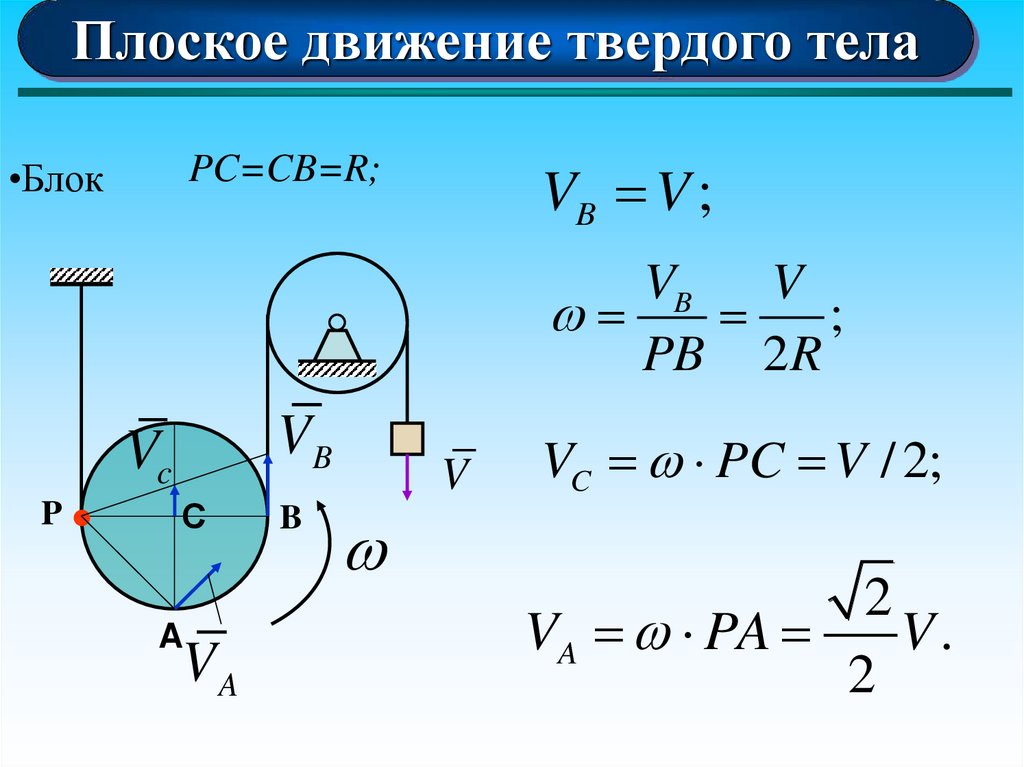
23.

Плоское движение твердого тела
VB V ;
PC=CB=R;
•Блок
VB
V
;
PB 2R
VB
Vc
P
С
A
VA
B
V
VC PC V / 2;
2
VA PA
V.
2

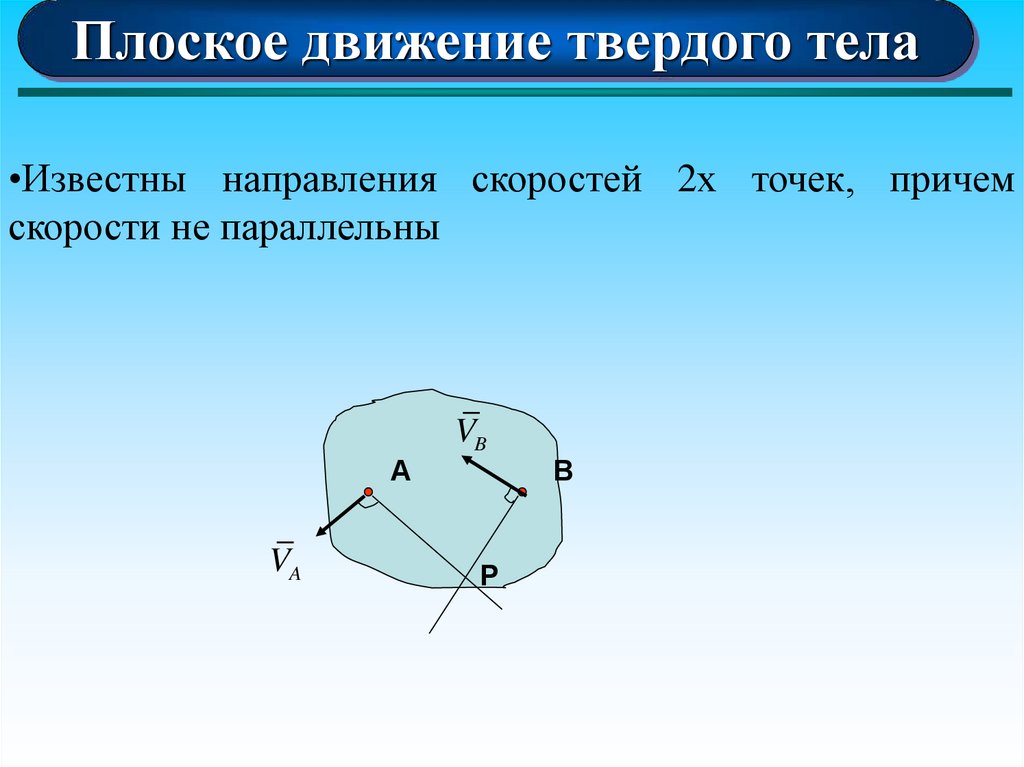
24.

Плоское движение твердого тела
•Известны направления скоростей 2х точек, причем
скорости не параллельны
А
VA
VB
Р
В

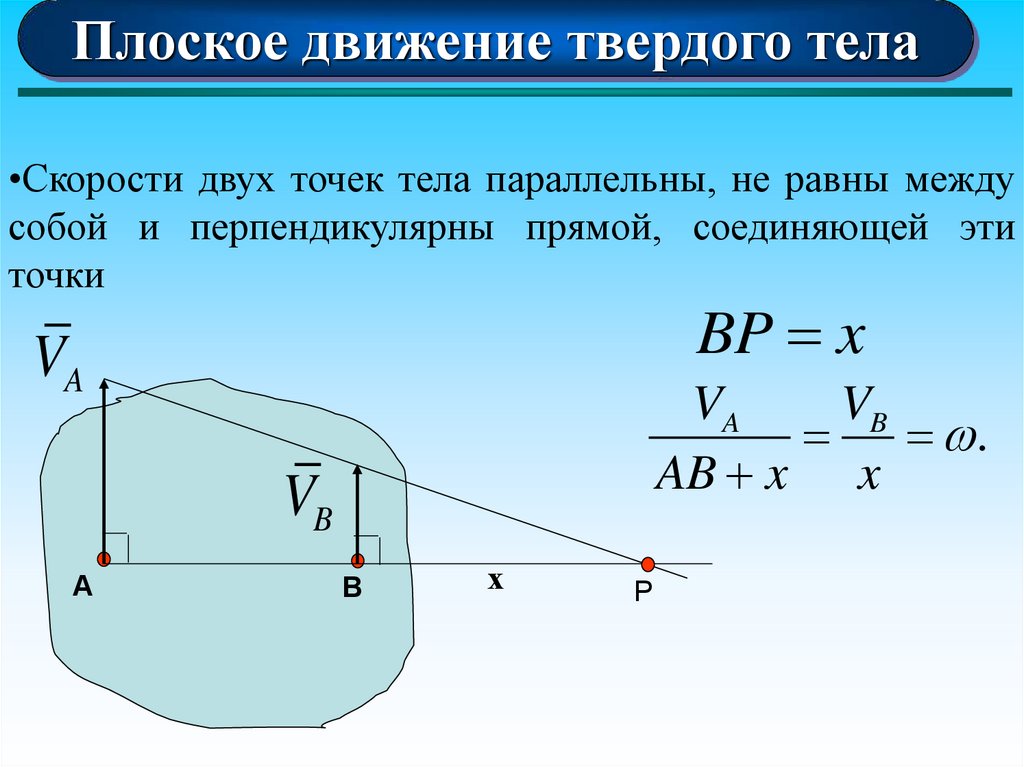
25.

Плоское движение твердого тела
•Скорости двух точек тела параллельны, не равны между
собой и перпендикулярны прямой, соединяющей эти
точки
BP x
VA
VA
VB
.
AB x x
VB
А
В
х
Р