Интеграл функции

1.

2.

Интеграл функции — сумма каких-либо чисел,
предназначенных для их интегрирования.
Процесс нахождения интеграла
называется интегрированием.
Согласно основной теореме анализа,
интегрирование является операцией,
обратной дифференцированию, чем помогает решать
дифференциальные уравнения.
Существует несколько различных определений операции
интегрирования, отличающихся в технических деталях.
Однако все они совместимы, то есть любые два способа
интегрирования, если их можно применить к данной
функции, дадут один и тот же результат. Наиболее простым
является интеграл Римана.

3.

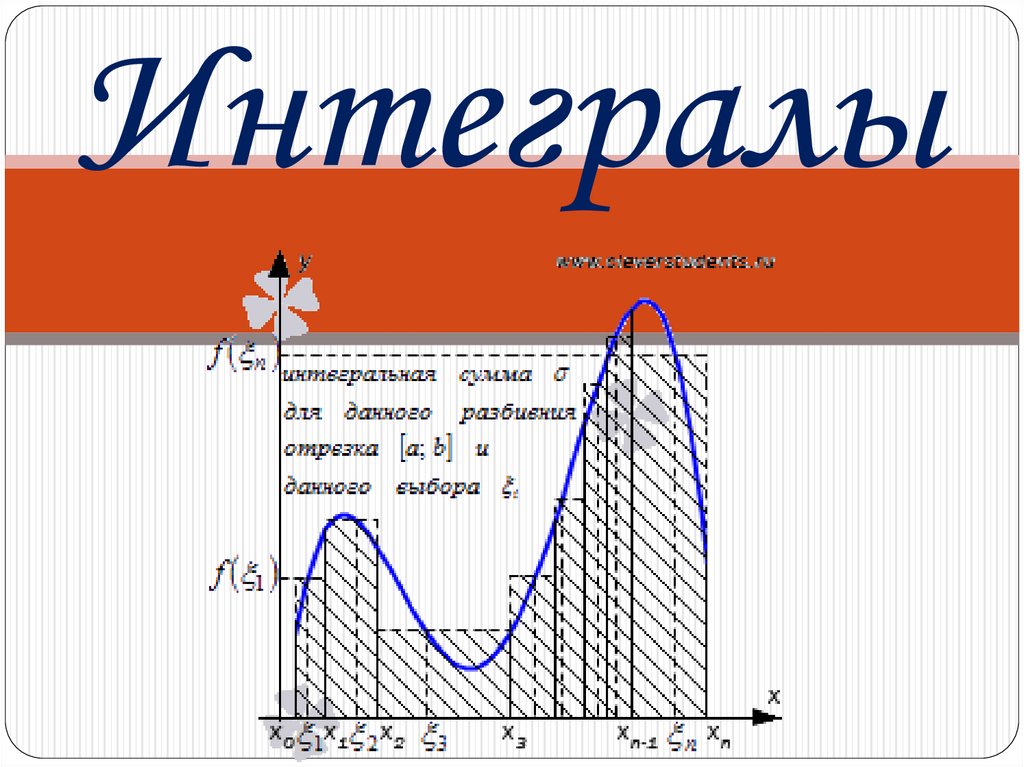
Риманова сумма (суммарная площадь прямоугольников) в пределе, при измельчении
разбиения, дает площадь подграфика.

4.

Неформально интеграл функции одной переменной можно ввести
как площади подграфика (фигуры, заключенной между графиком функции и осью
абсцисс).
Пытаясь найти эту площадь, можно рассматривать фигуры, состоящие из
некоторого количества вертикальных прямоугольников, основания которых
составляют вместе отрезок интегрирования и получаются при разбиении отрезка на
соответствующее количество маленьких отрезков.
Площадь S такой фигуры при каком-то конкретном разбиении на отрезки
длинами будет интегральной суммой:
В пределе - при «размельчении» разбиения (когда каждое
стремится к нулю)
интегральная сумма должна стремиться к интегралу функции f на отрезке:

5.

Альтернативная наглядная
интерпретация
Очень сходна интерпретация интеграла как сложения масс элементарных объемов при
нахождении массы неоднородного тела исходя из его плотности (являющейся
функцией координат):
В случае меньшей размерности области интегрирования (не 3, а 2 или 1) под
имеется в виду двумерная (поверхностная) или одномерная ("линейная")
плотность, а под
- элементарная площадь или элементарная длина
соответственно.
Для произвольной размерности n под
понимается n-мерный объем.

6.

• Определённый интеграл и Неопределённый интеграл
• Интеграл Римана и Римана — Стилтьеса
• Интеграл Лебега и Лебега — Стилтьеса
• Интеграл Даниэля

7.

Определённый интеграл — аддитивный монотонный функционал, заданный на
множестве пар, первая компонента которых есть интегрируемая функция или
функционал, а вторая — область в множестве задания этой функции (функционала).
Обозначения:
a - нижний предел.
b - верхний предел.
- подынтегральная функция.
- длина частичного отрезка.
- интегральная сумма от функции
на
соответствующей разбиению
- супремум длин частичных отрезков.

8.

Свойства
Если функция
интегрируема по Риману на
, то она ограничена на нем.
Геометрический смысл
Определённый интеграл
осью абсцисс, прямыми
численно равен площади фигуры, ограниченной
и
и графиком функции
.
Примеры вычислений
Далее приведены примеры взятий определенных интегралов с помощью формулы Ньютона — Лейбница.
1.
2.
3.

9.

Неопределённый интегра́л для функции
— это
совокупность всех первообразных данной функции.
Если функция
определена и непрерывна на
промежутке
и
- её первообразная, то
есть
при
, то
где С — произвольная постоянная.

10.

1. Метод введения нового аргумента. Если
то
Где
— непрерывно дифференцируемая функция.
2. Метод разложения. Если
то

11.

3. Метод подстановки. Если
где
— непрерывна, то, полагая
непрерывна вместе со своей производной
4. Метод интегрирования по частям. Если
дифференцируемые функции от x , то
и
, получим
— некоторые

12.

1.
2.
3.

13.

Интеграл Римана — Стилтьеса — обобщение определённого интеграла, предложенное в
1894 году Стилтьесом. Вместо предела обычных интегральных сумм
рассматривается предел сумм
где интегрирующая функция
есть функция с
ограниченным изменением (ограниченной вариацией). Если
дифференцируема, то он выражается через обычный интеграл:
непрерывно

14.

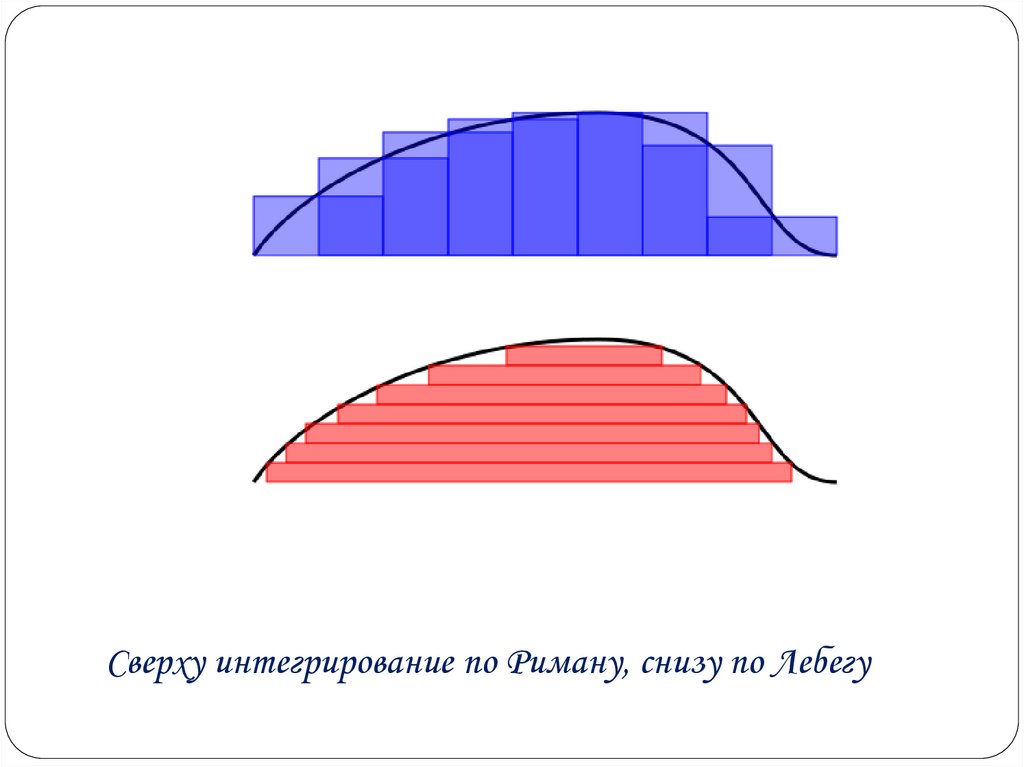
Интеграл Лебе́га— это обобщение интеграла Римана на
более широкий класс функций.
Все функции, определённые на конечном отрезке числовой
прямой и интегрируемые по Риману, являются также
интегрируемыми по Лебегу, причём в этом случае оба
интеграла равны. Однако существует большой класс функций,
определённых на отрезке и интегрируемых по Лебегу, но
неинтегрируемых по Риману. Также интеграл Лебега может
иметь смысл для функций, заданных на
произвольных множествах (интеграл Фреше).

15.

Сверху интегрирование по Риману, снизу по Лебегу

16.

Интеграл Лебега определяют пошагово, переходя от более простых
функций к сложным. Будем считать, что дано пространство с
мерой
, и на нем определена борелевская
функция
.
Определение 1. Пусть — индикатор некоторого измеримого множества,
то есть
, где
. Тогда интеграл Лебега функции
по
определению:

17.

Определение 2. Пусть
где
,а
множества. Тогда
— простая функция, то есть
— конечное разбиение
,
на измеримые
Определение 3. Пусть теперь — неотрицательная функция, то
есть
. Рассмотрим все простые функции
, такие
что
. Обозначим это семейство
. Для каждой функции
из этого семейства уже определён интеграл Лебега. Тогда интеграл от
задаётся
формулой:
Наконец, если функция произвольного знака, то её можно представить в виде разности
двух неотрицательных функций. Действительно, легко видеть, что:
где

18.

Определение 4. Пусть — произвольная измеримая функция.
Тогда ее интеграл задаётся формулой:
Определение 5. Пусть наконец
множество. Тогда по определению
Где
произвольное измеримое
— индикатор-функция множества А .

19.

Интеграл Лебега линеен, то есть
Где
— произвольные константы;
Интеграл Лебега сохраняет неравенства, то есть
если
почти всюду,
измерима
и
интегрируема, то интегрируема и
, и более того
Интеграл Лебега не зависит от поведения функции на множестве меры
нуль, то есть если
почти всюду, то

20.

Интеграл Даниеля — одно из обобщений интеграла Римана,
альтернативное понятию интеграла Лебега.
В сравнении с интегралом Лебега, интеграл Даниеля не требует
предварительной разработки подходящей теории меры, за счёт чего
имеет определённые преимущества, особенно в функциональном
анализе при обобщении на пространства высших размерностей и
дальнейших обобщениях (например, в форме интеграла Стилтьеса).
Конструкции Лебега и Даниеля эквивалентны, если рассматривать в
качестве элементарных ступенчатые функции, однако при
обобщении понятия интеграла на более сложные объекты
(например, линейные функционалы) возникают существенные
трудности в построении интеграла по Лебегу, тогда как интеграл
Даниеля строится в этих случаях относительно просто.

21.

Определение
Основная идея состоит в обобщении понятия интеграла, исходя о
представлении о нём как о функционале. Рассмотрим семейство H
ограниченных вещественнозначных функций (называемых элементарными
функциями), определённых на пространстве X , удовлетворяющее следующим
аксиомам:
1. Если
, то
.
2. Если
, то
, где c — действительное число.
3. Если
, то
и
.
На классе H задан функционал
1.
.
2.
.
3. Если
и
Лебега).
4.
, если
, обладающий следующими свойствами:
, то
(свойство

22.

Области интегрирования
•Кратный интеграл
В математическом анализе кратным или многократным интегралом называют
множество интегралов, взятых от
переменных. Например:
Замечание: кратный интеграл − это определённый интеграл, при его вычислении
всегда получается число.

23.

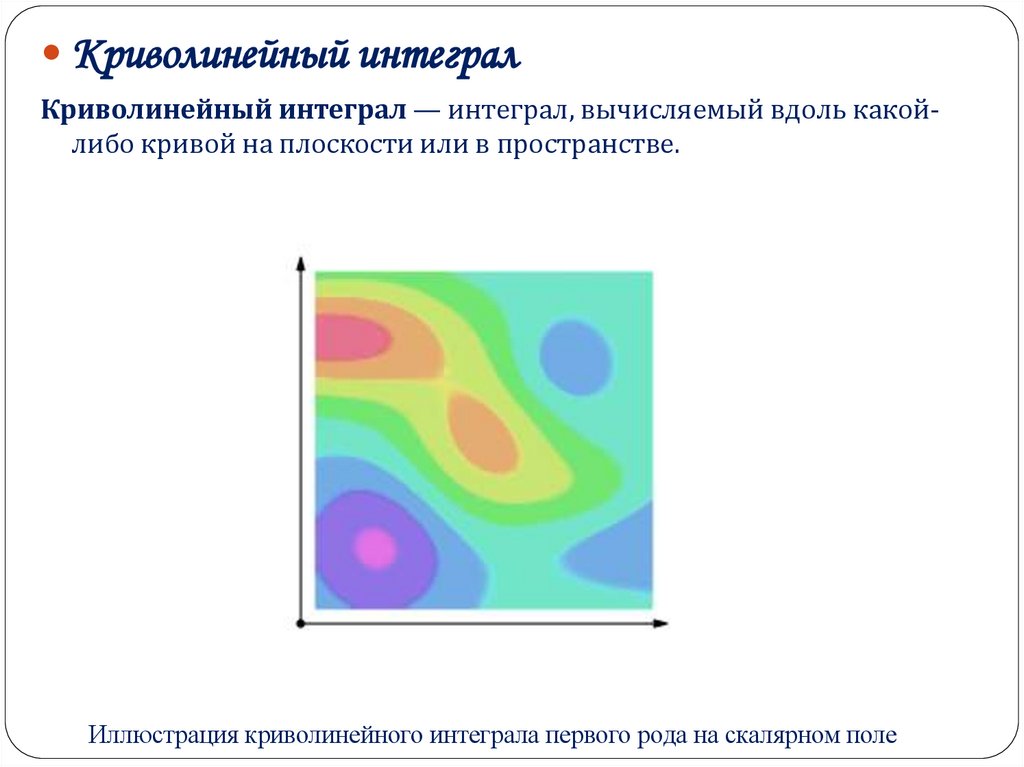
Криволинейный интеграл
Криволинейный интеграл — интеграл, вычисляемый вдоль какойлибо кривой на плоскости или в пространстве.
Иллюстрация криволинейного интеграла первого рода на скалярном поле

24.

Криволинейный интеграл первого рода.
Свойства.
1.
Линейность:
2.
Аддитивность: если
3.
Монотонность: если
4.
Теорема о среднем для непрерывной вдоль
5.
Изменение направления обхода кривой интегрирования не влияет на знак
интеграла:
6.
Криволинейный интеграл первого рода не зависит от параметризации
кривой.
в одной точке, то
на
, то
функции
:

25.

Криволинейный интеграл второго рода.
Иллюстрация криволинейного интеграла второго рода на векторном поле

26.

Свойства.
1.
Линейность:
2.
Аддитивность:
3.
Замечание. Для криволинейных интегралов второго рода несправедливы
свойство монотонности, оценка модуля и теорема о среднем.

27.

Дифференцирование по параметру
Пусть задан интеграл вида
В таком случае, производная по параметру t будет равна