B_11. Вычисление объема многогранников

1.

Открытый банк заданий по математике http://mathege.ru:8080/or/ege/Main.action

2.

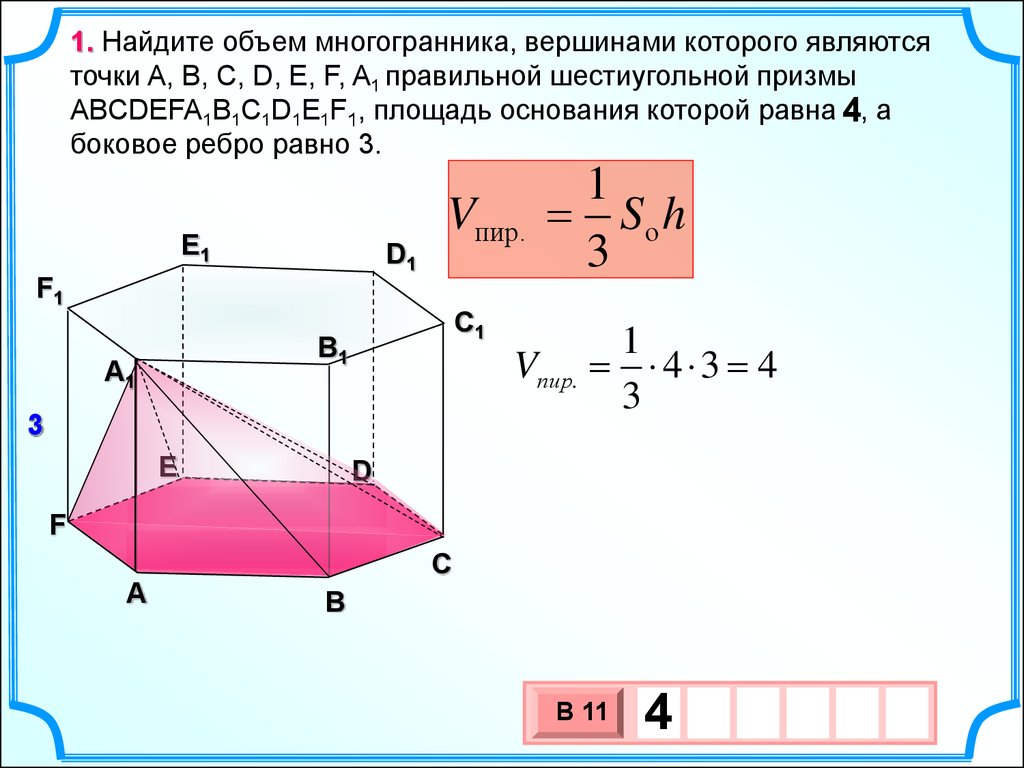
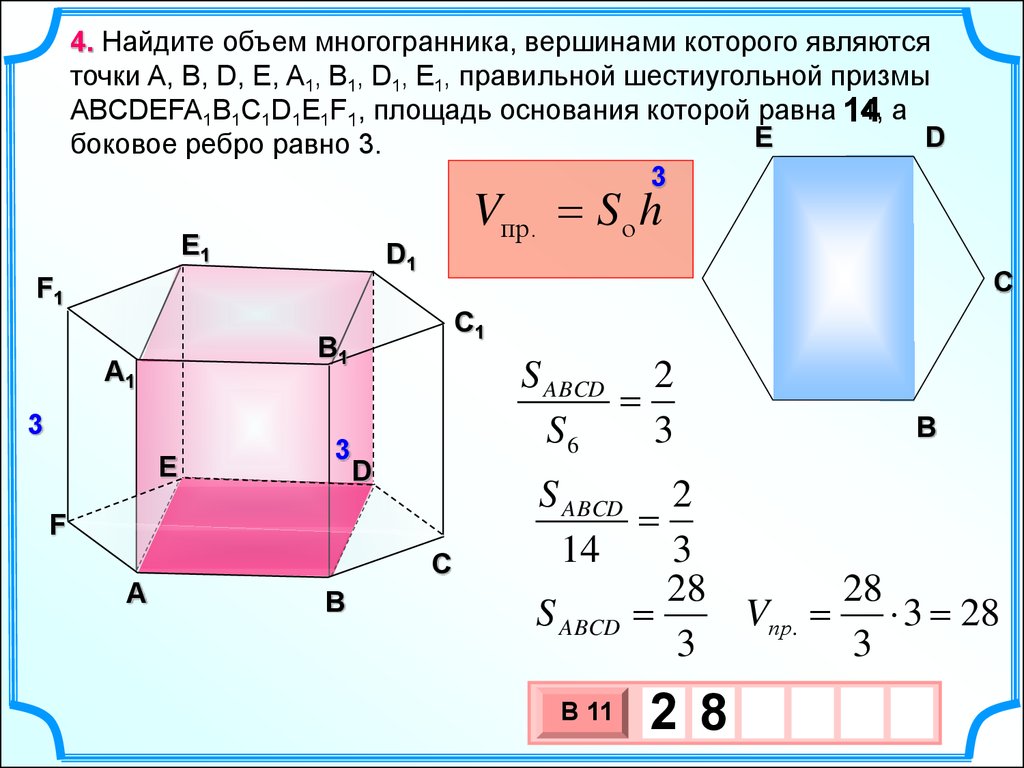
1. Найдите объем многогранника, вершинами которого являются
точки A, B, C, D, E, F, A1 правильной шестиугольной призмы
ABCDEFA1B1C1D1E1F1, площадь основания которой равна 4
4, а
боковое ребро равно 3.
E1
D1
Vпир.
1
Sо h
3
F1
C1
B1
А1
Vпир.
3
E
1
4 3 4
3
D
F
А
C
B
В 11
4
3
10 х
х

3.

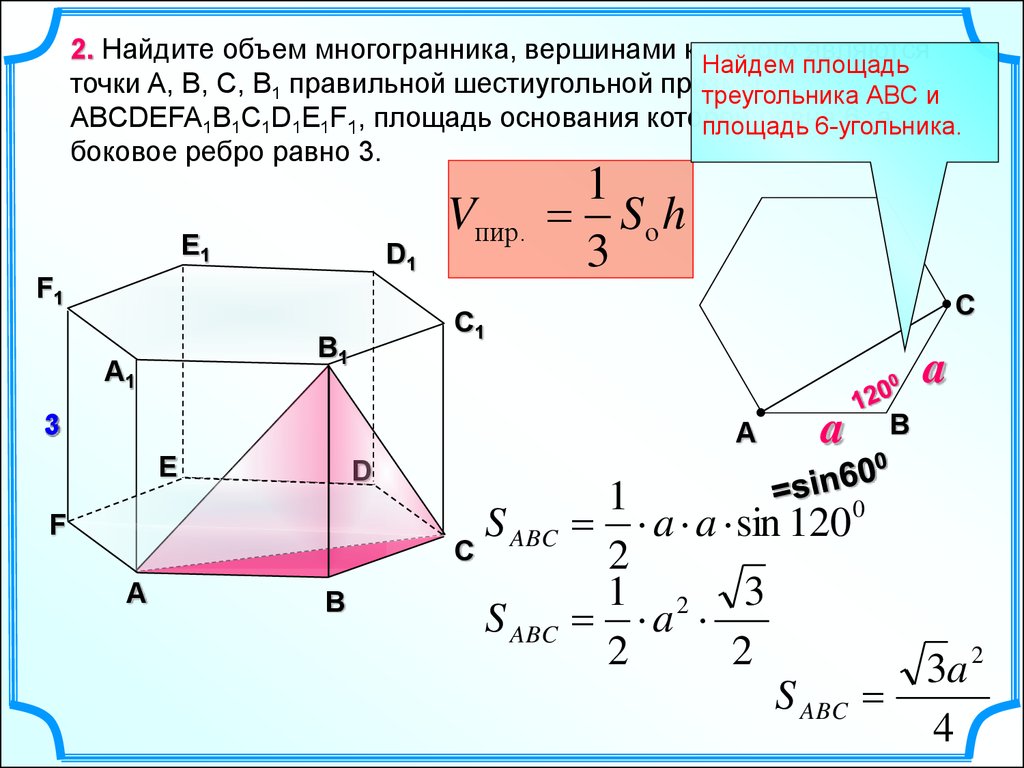
2. Найдите объем многогранника, вершинами которого являются
Найдем площадь
точки A, B, C, B1 правильной шестиугольной призмы
треугольника АВС и
ABCDEFA1B1C1D1E1F1, площадь основания которой
равна
6, а
площадь
6-угольника.
боковое ребро равно 3.
E1
D1
Vпир.
1
Sо h
3
F1
B1
А1
C
C1
a
3
А
E
D
F
C
А
B
S ABC
S ABC
a
B
1
0
a a sin 120
2
1 2 3
a
2
2
3a 2
S ABC
4

4.

1
S6 6 a a sin 600
2
2
3
3
a
3
2
3 a
2
2
Вычислить площадь правильного
6-угольника можно разбив его на
6 треугольников.
S ABC
3a 2
4
a
a
Найдем, какую часть составляет
площадь треугольника АВС от
всего 6-угольника.
S ABC
1
3a 2 3 3a 2
3a 2
2
:
S6
4
2
4 3 3a 2 6
Значит, площадь треугольника АВС в 6 раз
меньше площади шестиугольника.

5.

D
C
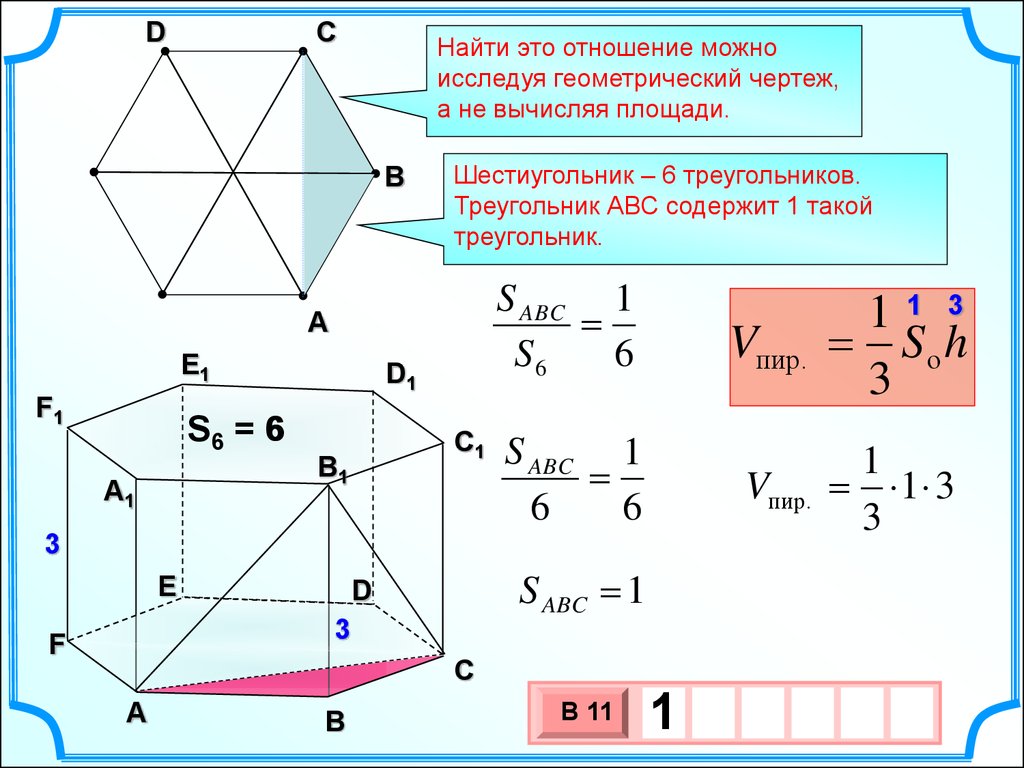
Найти это отношение можно
исследуя геометрический чертеж,
а не вычисляя площади.
B
Шестиугольник – 6 треугольников.
Треугольник АВС содержит 1 такой
треугольник.
S ABC 1
S6
6
A
E1
F1
D1
S6 = 6
C1
B1
А1
S ABC 1
6
6
Vпир.
11 3
Sо h
3
Vпир.
1
1 3
3
3
E
S ABC 1
D
3
F
C
А
B
В 11
1
3
10 х
х

6.

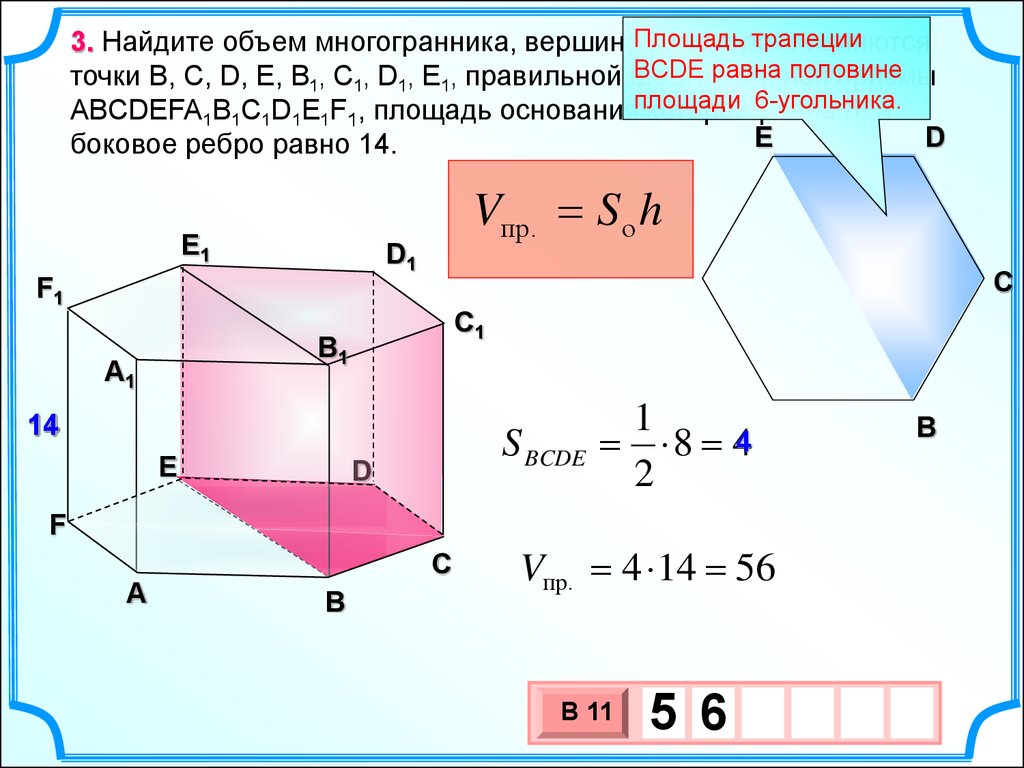
Площадь
трапеции
3. Найдите объем многогранника, вершинами
которого
являются
BCDE равна половине
точки B, C, D, E, B1, C1, D1, E1, правильной шестиугольной
призмы
ABCDEFA1B1C1D1E1F1, площадь основанияплощади
которой 6-угольника.
равна 8, а
E
D
боковое ребро равно 14.
Vпр. S о h
E1
D1
C
F1
C1
B1
А1
14
E
S BCDE
D
1
8 44
2
B
F
А
C
B
Vпр. 4 14 56
В 11
5 6
3
10 х
х

7.

Найдем
площадь
64. Найдите объем многогранника, вершинами
которого
являются
угольника и
точки A, B, D, E, A1, B1, D1, E1, правильной шестиугольной
призмы
ABCDEFA1B1C1D1E1F1, площадь основанияпрямоугольника.
которой равна 14, а
E
D
боковое ребро равно 3.
Vпр. S о h
E1
a
D1
a
F1
S6
3
E
D
C
B
3a
2
a
3
a
2
B
BD 2 a 2 a 2 2a a cos1200
F
А
C
C1
B1
А1
3
1
BD 2a 2a
2
2
2
BD 3a
2
2
BD a 3
2
S ABDE a 2 3

8.

S ABDE a
2
3a 2 3
S6
2
3
2
2
S ABDЕ
2
3
3
a
a
3
2
2
a 3 :
2
S6
3
2
1 3 3a
E
D
Найдем, какую часть составляет
площадь прямоугольника АВСD
от всего 6-угольника.
C
B
Найти это отношение можно
исследуя геометрический чертеж,
а не вычисляя площади.
Шестиугольник – 6 треугольников.
Прямоугольник содержит 4 таких
же треугольника.
S ABDЕ 4 2
S6
6 3

9.

4. Найдите объем многогранника, вершинами которого являются
точки A, B, D, E, A1, B1, D1, E1, правильной шестиугольной призмы
ABCDEFA1B1C1D1E1F1, площадь основания которой равна 14
14, а
E
D
боковое ребро равно 3.
3
Vпр. S о h
E1
D1
C
F1
C1
B1
А1
3
E
3
S ABCD 2
S6
3
D
F
А
C
B
B
S ABCD 2
14
3
28
28
S ABCD
Vпр. 3 28
3
3
В 11
2 8
3
10 х
х

10.

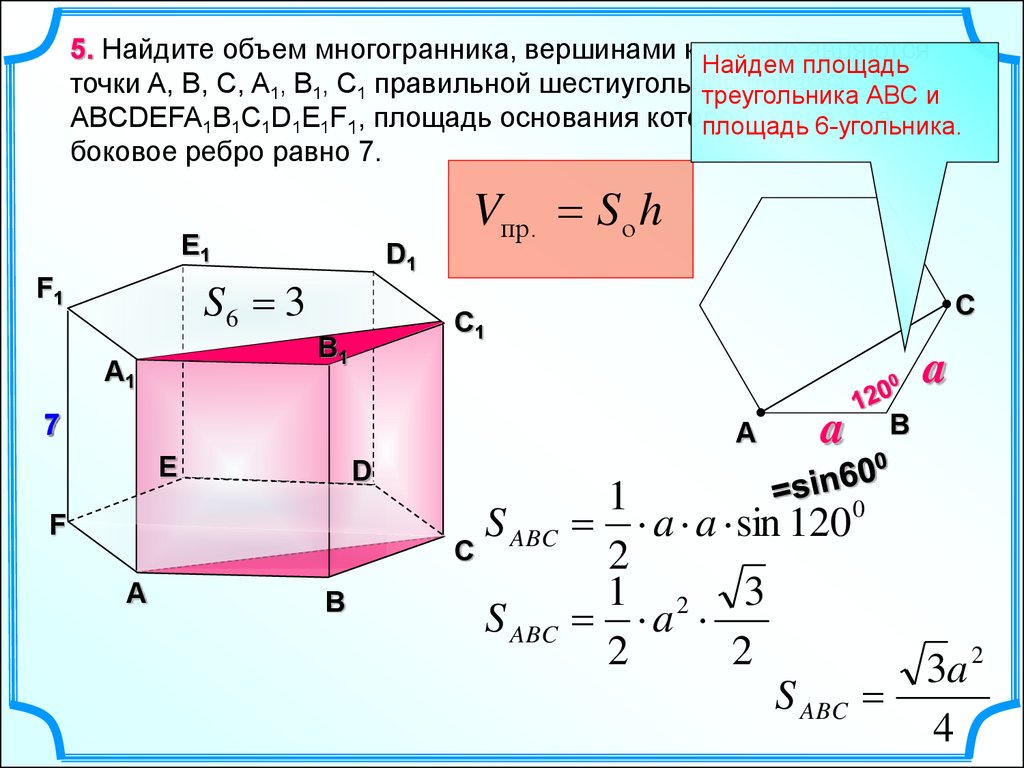
5. Найдите объем многогранника, вершинами которого являются
Найдем площадь
точки A, B, C, A1, B1, C1 правильной шестиугольной
призмы АВС и
треугольника
ABCDEFA1B1C1D1E1F1, площадь основания которой
равна
3, а
площадь
6-угольника.
боковое ребро равно 7.
Vпр. S о h
E1
D1
S6 3
F1
B1
А1
C
C1
a
7
А
E
D
F
C
А
B
S ABC
S ABC
a
B
1
0
a a sin 120
2
1 2 3
a
2
2
3a 2
S ABC
4

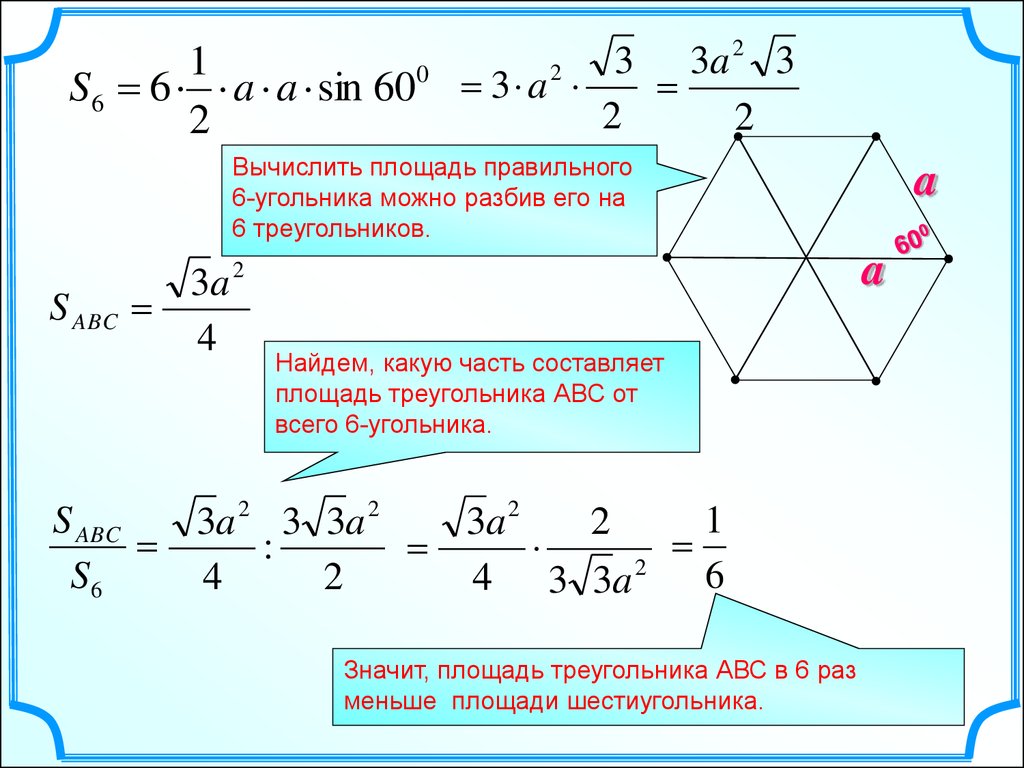
11.

1
S6 6 a a sin 600
2
2
3
3
a
3
2
3 a
2
2
Вычислить площадь правильного
6-угольника можно разбив его на
6 треугольников.
S ABC
3a 2
4
a
a
Найдем, какую часть составляет
площадь треугольника АВС от
всего 6-угольника.
S ABC
1
3a 2 3 3a 2
3a 2
2
:
S6
4
2
4 3 3a 2 6
Значит, площадь треугольника АВС в 6 раз
меньше площади шестиугольника.

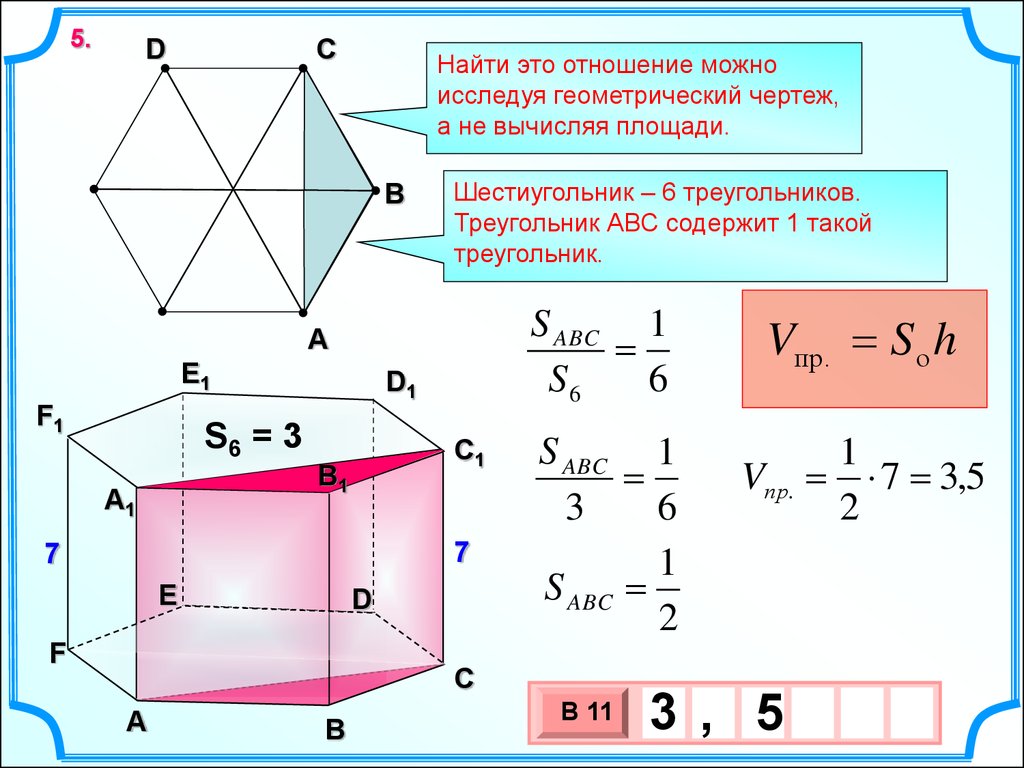
12.

5.
D
C
Найти это отношение можно
исследуя геометрический чертеж,
а не вычисляя площади.
B
Шестиугольник – 6 треугольников.
Треугольник АВС содержит 1 такой
треугольник.
S ABC 1
S6
6
A
E1
F1
D1
S6 = 3
C1
B1
А1
7
7
E
D
F
S ABC 1
3
6
1
S ABC
2
C
А
B
В 11
Vпр. S о h
Vпр.
3 , 5
1
7 3,5
2
3
10 х
х

13.

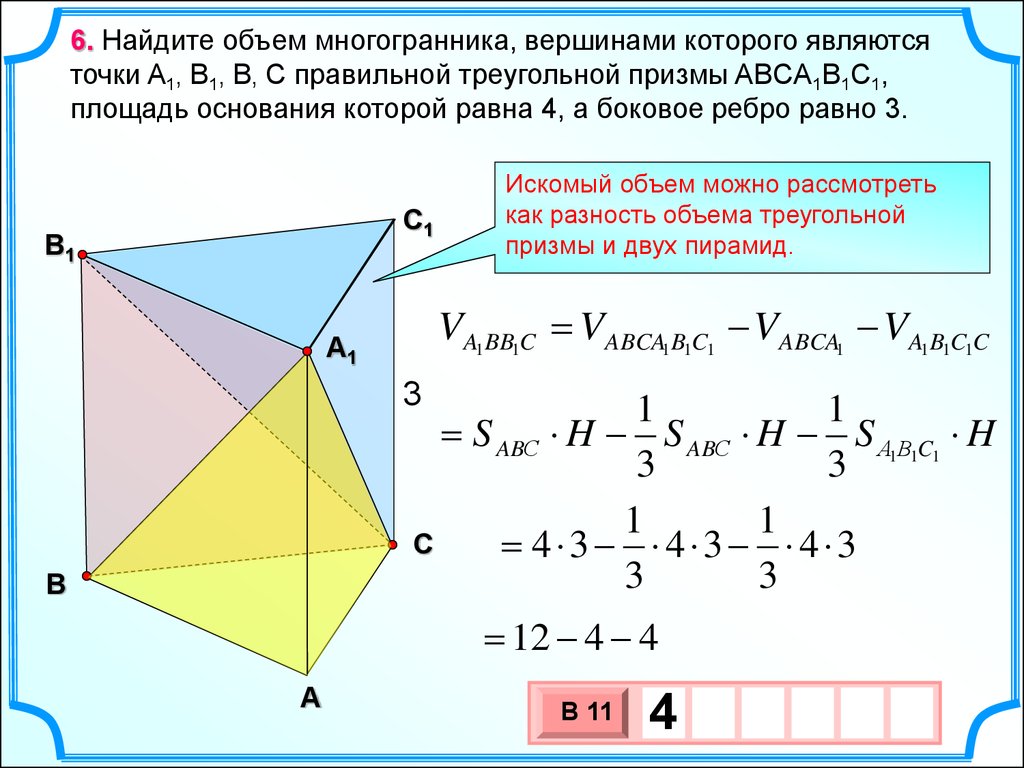
6. Найдите объем многогранника, вершинами которого являются
точки A1, B1, В, С правильной треугольной призмы ABCA1B1C1,
площадь основания которой равна 4, а боковое ребро равно 3.
С1
В1
Искомый объем можно рассмотреть
как разность объема треугольной
призмы и двух пирамид.
VA1BB1C VABCA1B1C1 VABCA1 VA1B1C1C
А1
3
1
1
S ABС H S ABС H S А1В1C1 H
3
3
1
1
С
4 3 4 3 4 3
3
3
В
12 4 4
А
В 11
4
3
10 х
х

14.

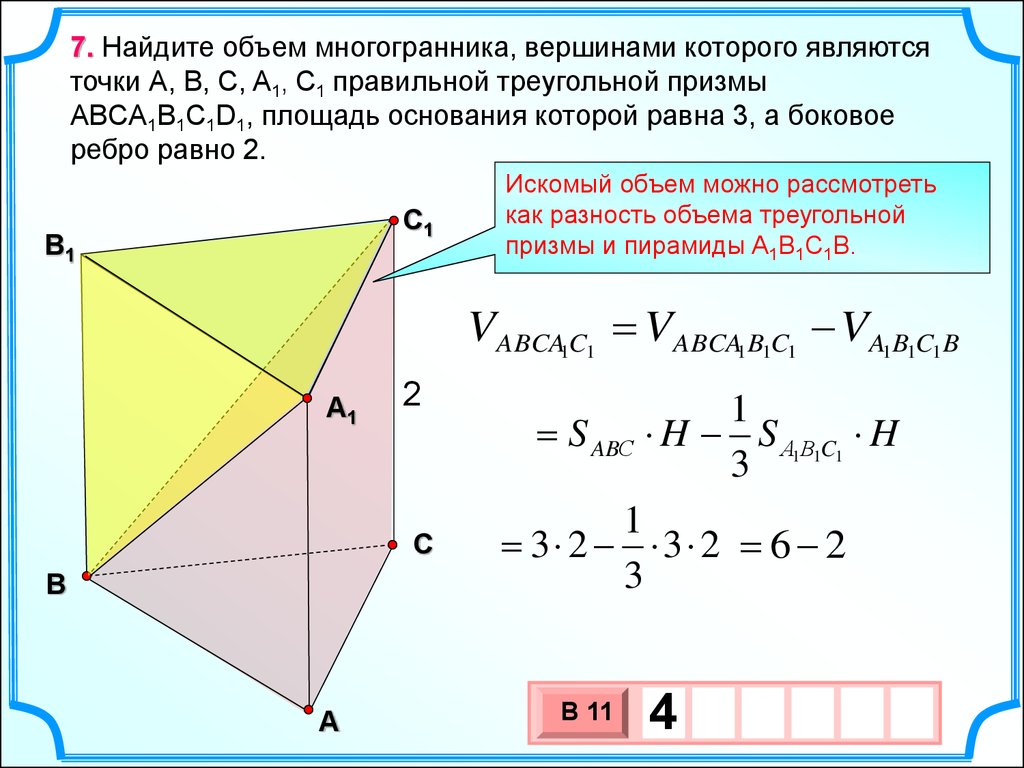
7. Найдите объем многогранника, вершинами которого являются
точки А, В, С, A1, С1 правильной треугольной призмы
ABCA1B1C1D1, площадь основания которой равна 3, а боковое
ребро равно 2.
С1
В1
Искомый объем можно рассмотреть
как разность объема треугольной
призмы и пирамиды A1B1C1B.
VABCA1C1 VABCA1B1C1 VA1B1C1B
А1
2
С
В
А
1
S ABС H S А1В1C1 H
3
1
3 2 3 2 6 2
3
В 11
4
3
10 х
х

15.

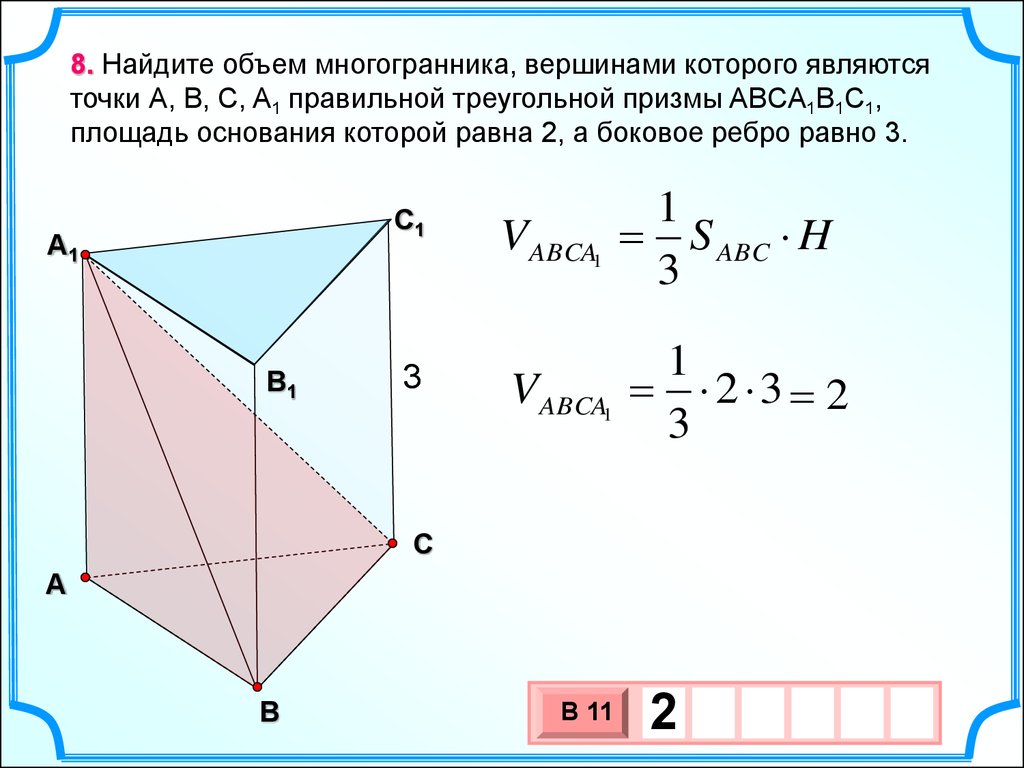
8. Найдите объем многогранника, вершинами которого являются
точки А, В, С, A1 правильной треугольной призмы ABCA1B1C1,
площадь основания которой равна 2, а боковое ребро равно 3.
С1
А1
В1
3
VABCA1
1
S ABC H
3
VABCA1
1
2 3 2
3
С
А
В
В 11
2
3
10 х
х

16.

9. Найдите объем многогранника, вершинами которого являются
точки А, В, C, B1 прямоугольного параллелепипеда ABCDA1B1C1D1,
у которого АВ=3, АD=3, AA1=3.
C1
B1
33
D1
1
S = ab
2
A1
3
C
B
3
D
VABCB1
1
S ABC H
3
3
1 1
VABCB1 3 3 3
3 2
9
V ABCB1
2
А
В 11
4 , 5
3
10 х
х

17.

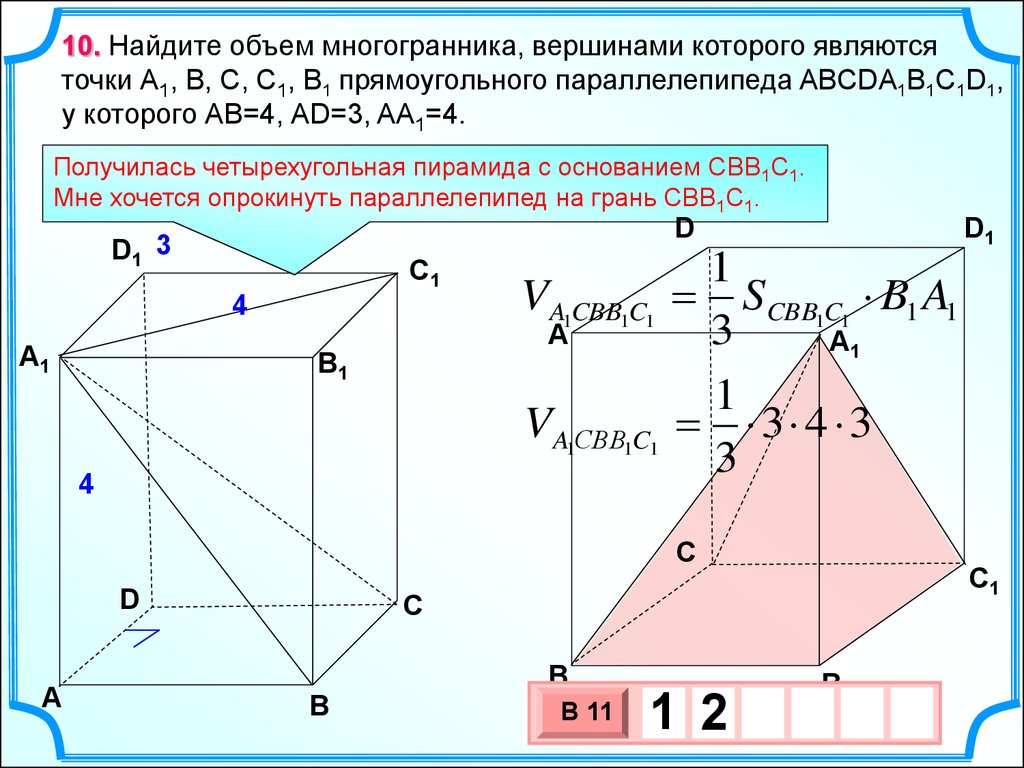
10. Найдите объем многогранника, вершинами которого являются
точки А1, В, C, C1, B1 прямоугольного параллелепипеда ABCDA1B1C1D1,
у которого АВ=4, АD=3, AA1=4.
Получилась четырехугольная пирамида с основанием СВВ1С1.
Мне хочется опрокинуть параллелепипед на грань CBВ1C1.
D
D1 3
C1
4
A1
B1
4
D1
1
VA1CBB1C1 SCBB1C1 B1 A1
3
A
A1
1
VA1СBB1C1 3 4 3
3
C
D
A
C1
C
B
B
В 11
1 2
3
10 х
B1
х

18.

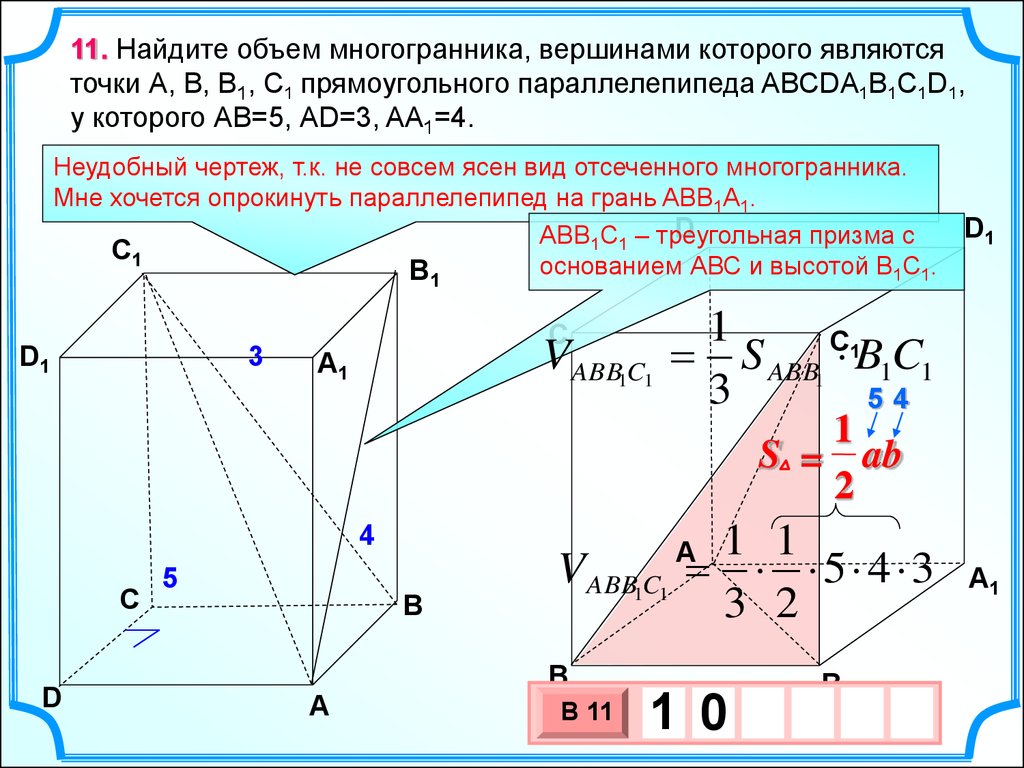
11. Найдите объем многогранника, вершинами которого являются
точки А, В, B1, C1 прямоугольного параллелепипеда ABCDA1B1C1D1,
у которого АВ=5, АD=3, AA1=4.
Неудобный чертеж, т.к. не совсем ясен вид отсеченного многогранника.
Мне хочется опрокинуть параллелепипед на грань ABВ1А1.
D
АВВ1С1 – треугольная
призма с
C1
основанием АВС и высотой В1С1.
B1
D1
3
C
VABB1C1
A1
D1
1
S ABB1 C 1B1C1
3
54
1
S = ab
2
4
C
D
5
B
VABB1C1
1 1
5 4 3
3 2
A
B
A
В 11
1 0
3
10 х
B1
х
A1

19.

12. Найдите объем многогранника, вершинами которого являются
точки А, В, C, D1 прямоугольного параллелепипеда ABCDA1B1C1D1,
у которого АВ=4, АD=3, AA1=4.
C1
B1
D1
VABCD1
A1
1
S ABC DD1
3
34
1
S = ab
2
4
C
B
VABСB1
4
D
3
1 1
3 4 4
3 2
A
В 11
8
3
10 х
х

20.

13. Найдите объем многогранника, вершинами которого являются
точки А, D, A1, B, C, B1 прямоугольного параллелепипеда ABCDA1B1C1D1,
у которого АВ=3, АD=4, AA1=5.
D1
C1
A1
Диагональное сечение делит
параллелепипед на два равных
многогранника. Равные фигуры имеют
равные объемы.
В1
VABCDB1 A1
1
VABCDA1B1C1D1
2
VABCDB1 A1
1
5 3 4
2
5
D
C
4
A
3
В
В 11
3 0
3
10 х
х