Similar presentations:
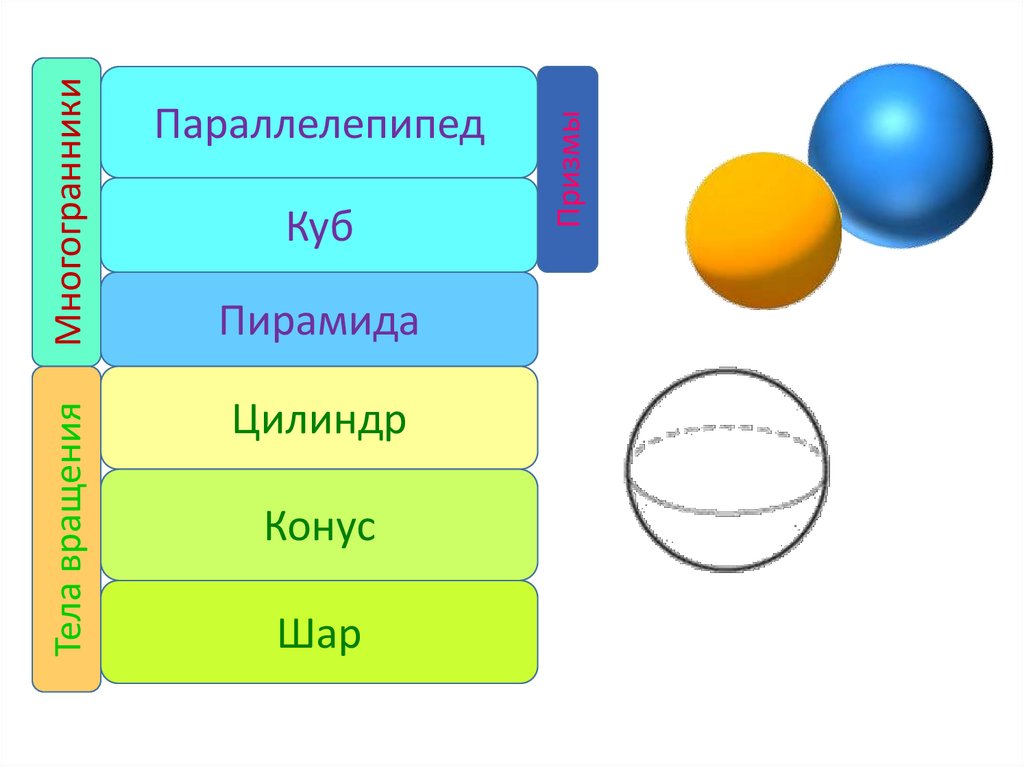
Многогранники
1.
2.
КубПирамида
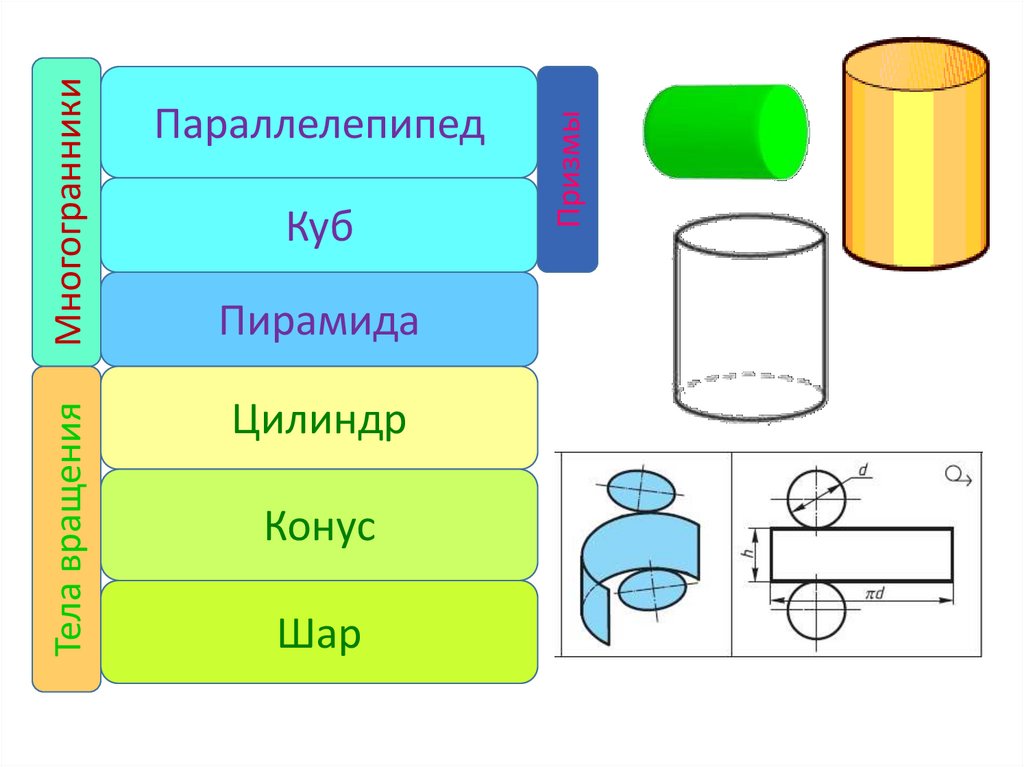
Цилиндр
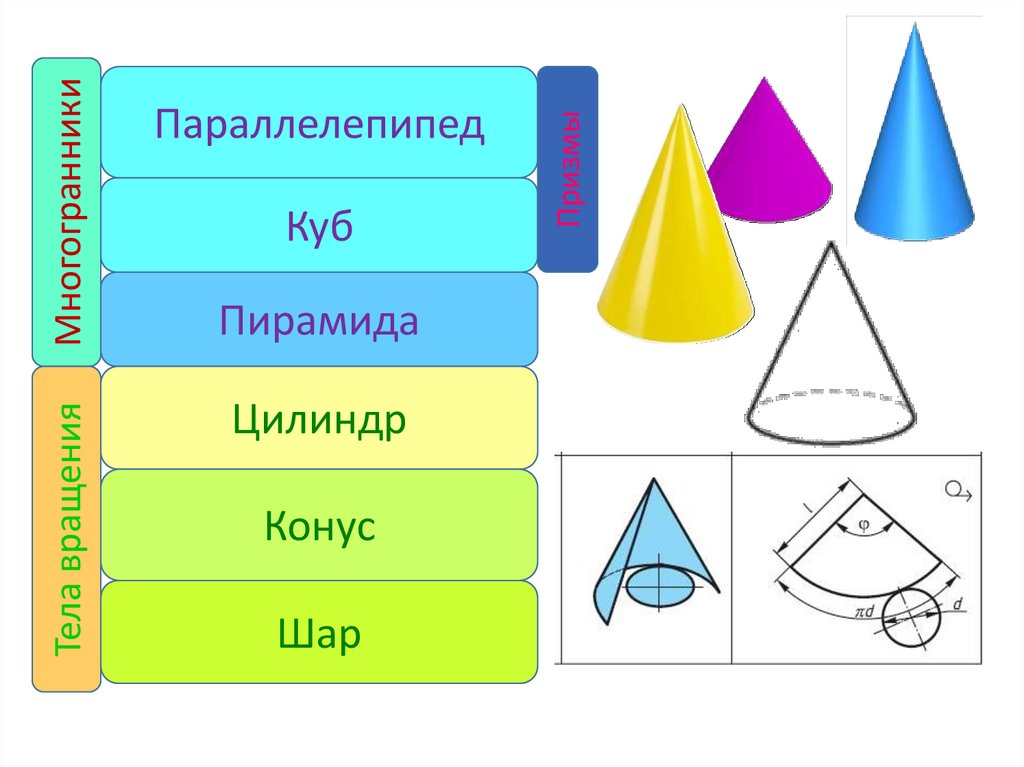
Конус
Шар
Призмы
Многогранники
Тела вращения
Параллелепипед
В математике важны формы
предметов, их размеры, поэтому
вместо предметов
рассматриваются геометрические
тела, названия которых во многих
случаях произошли от
соответствующих предметов.
3.
КубПирамида
Цилиндр
Конус
Шар
Призмы
Многогранники
Тела вращения
Параллелепипед
4.
КубПирамида
Цилиндр
Конус
Шар
Призмы
Многогранники
Тела вращения
Параллелепипед
5.
КубПирамида
Цилиндр
Конус
Шар
Призмы
Многогранники
Тела вращения
Параллелепипед
6.
КубПирамида
Цилиндр
Конус
Шар
Призмы
Многогранники
Тела вращения
Параллелепипед
7.
КубПирамида
Цилиндр
Конус
Шар
Призмы
Многогранники
Тела вращения
Параллелепипед
8.
КубПирамида
Цилиндр
Конус
Шар
Призмы
Многогранники
Тела вращения
Параллелепипед
9. Многообразие геометрических форм вокруг нас на примере зданий
10.
11. Поверхность каждого геометрического тела делит пространство на внутреннюю и внешнюю области. Поверхность шара называют сферой
(«сфера» — латинская форма греческогослова «сфайра» — шар).
12.
13.
Многогранник –геометрическое тело,
ограниченное со всех
сторон плоскими
многоугольниками.
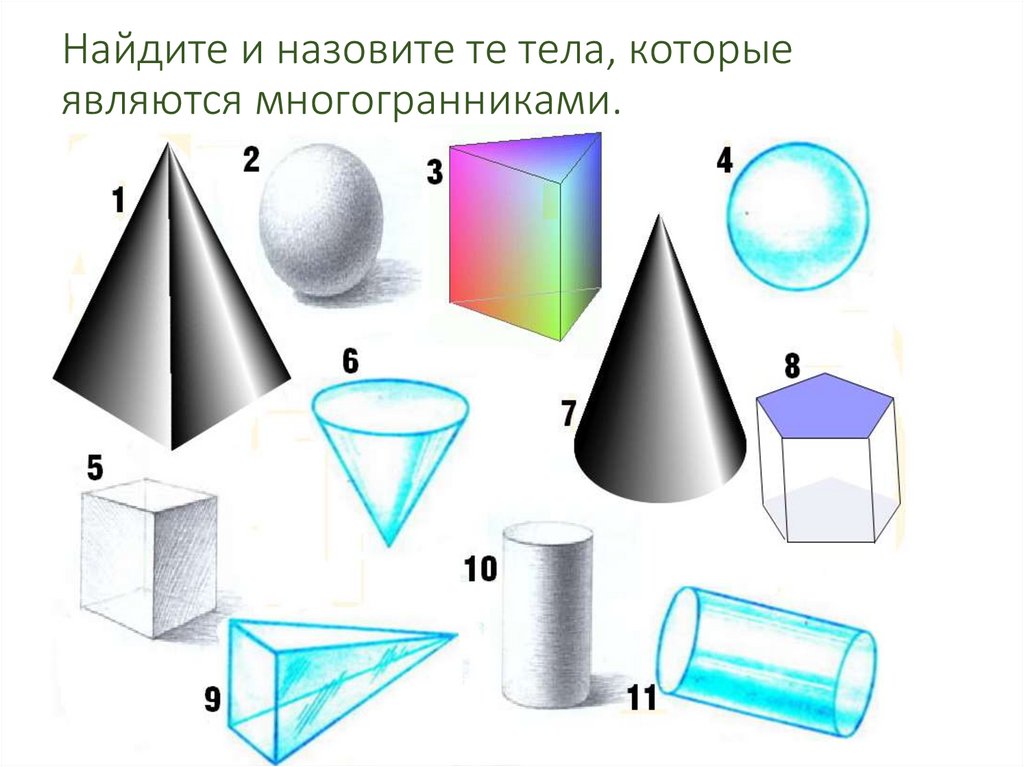
14. Найдите и назовите те тела, которые являются многогранниками.
15. Многогранники
Поверхность любогомногогранника состоит из
многоугольников. Каждый из
многоугольников называют
гранью многогранника, вершины этих
многоугольников – вершинами многогранника,
а стороны – ребрами.
16.
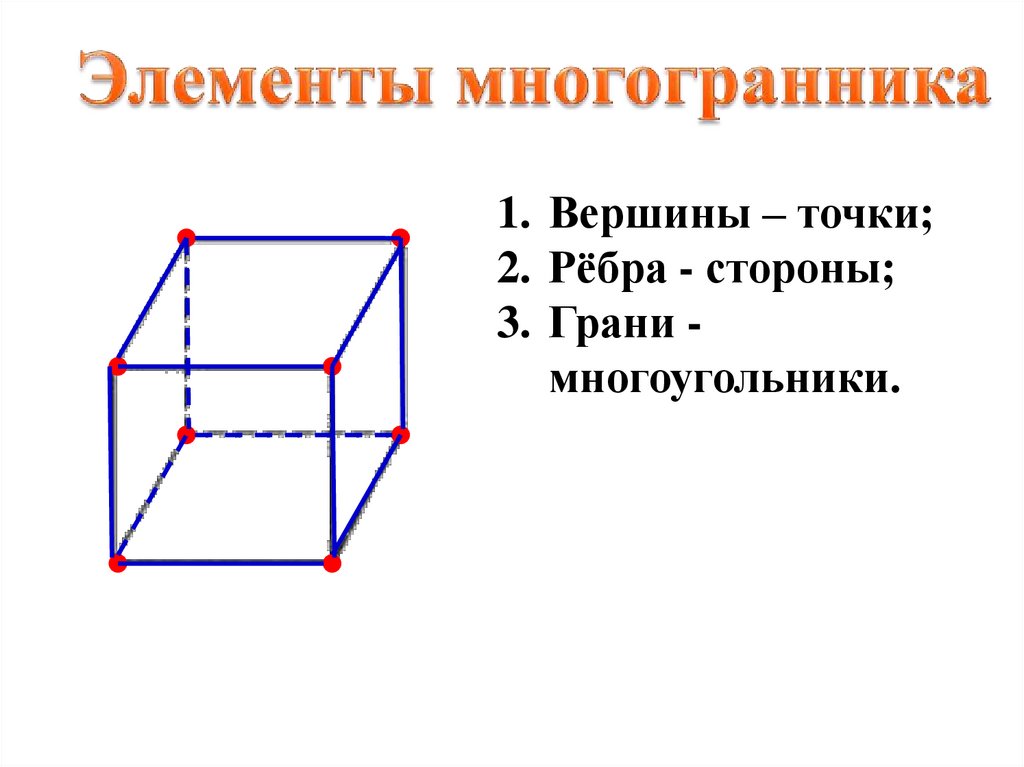
1. Вершины – точки;2. Рёбра - стороны;
3. Грани многоугольники.
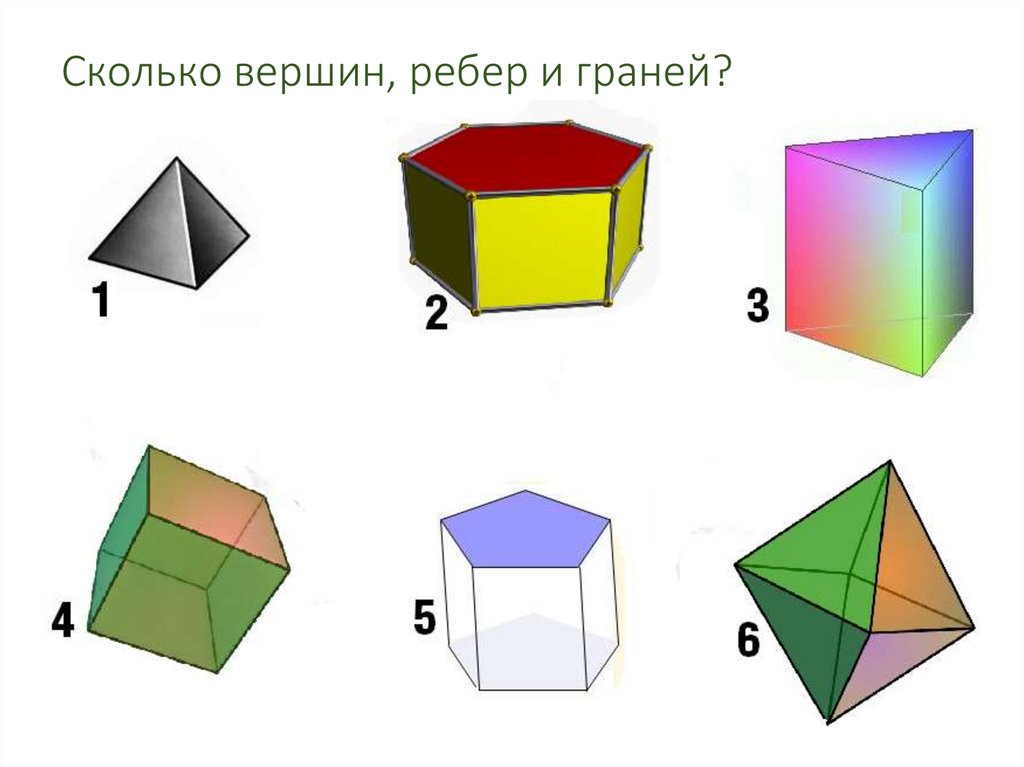
17. Сколько вершин, ребер и граней?
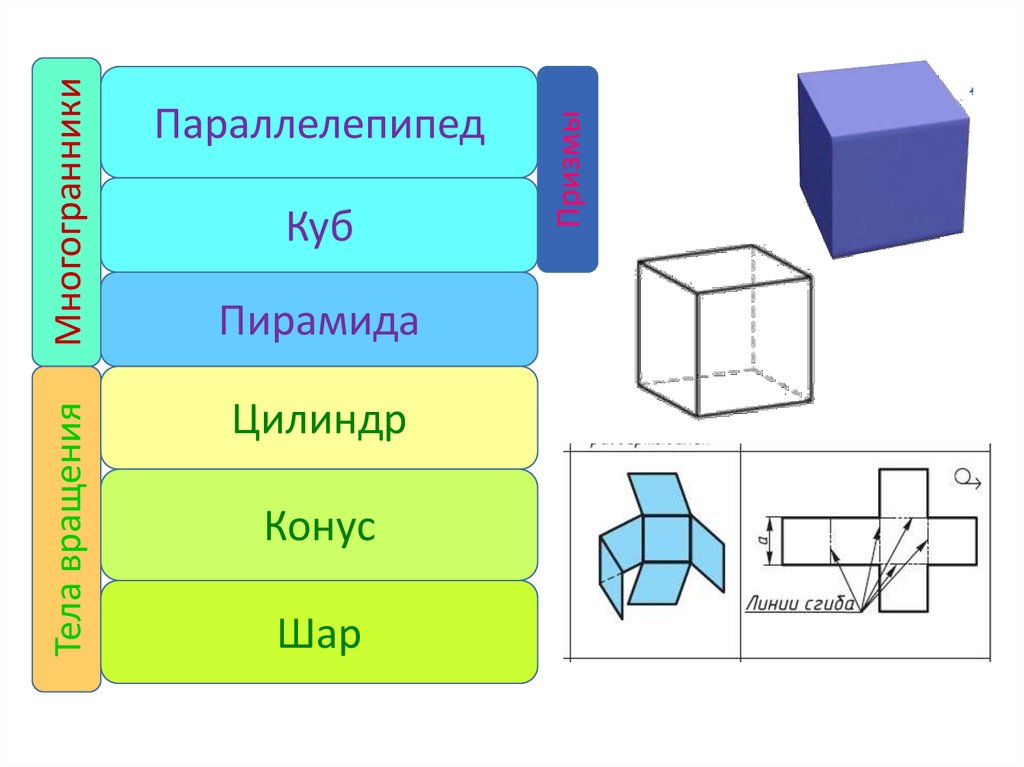
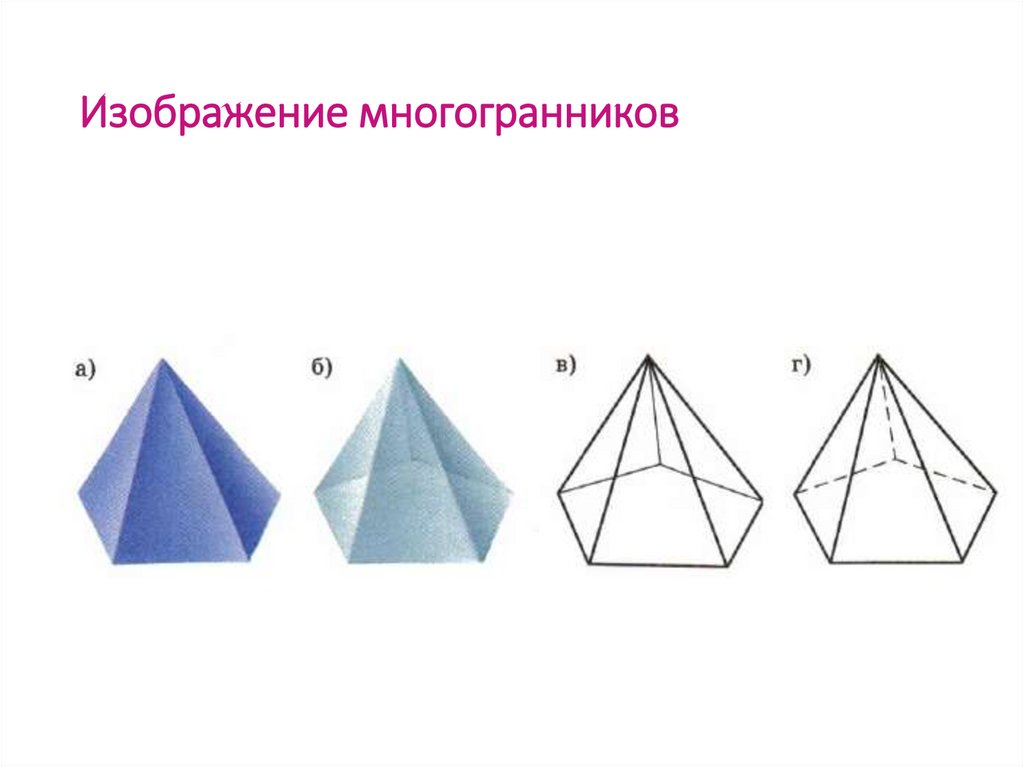
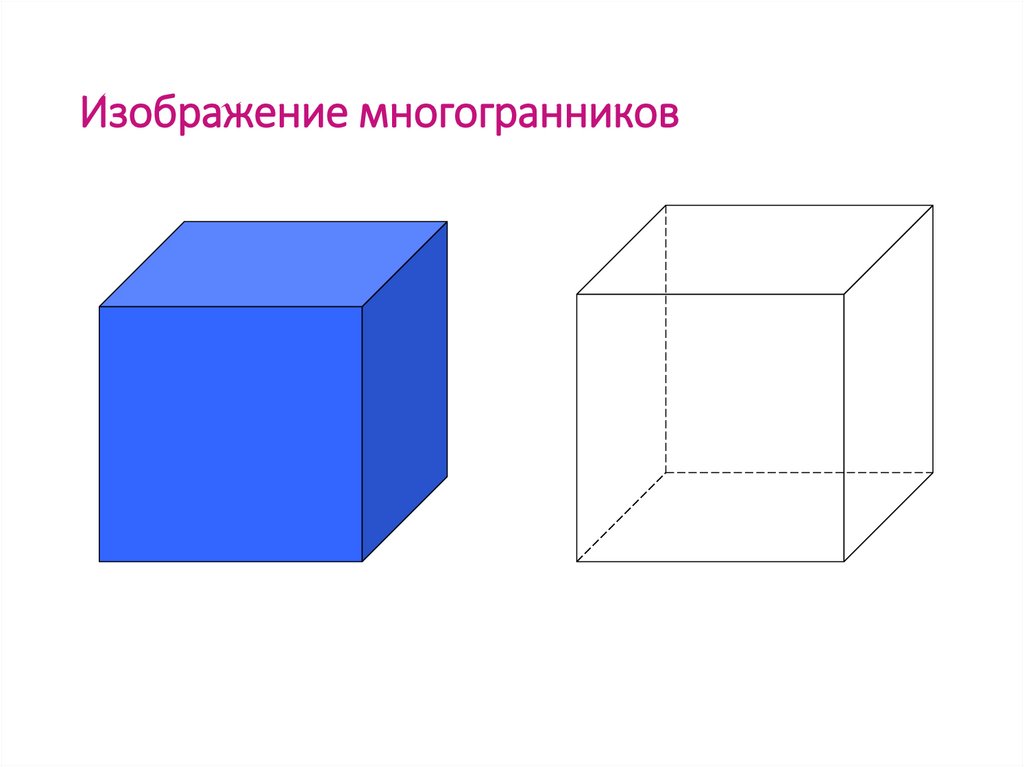
18. Изображение многогранников
1819. Изображение многогранников
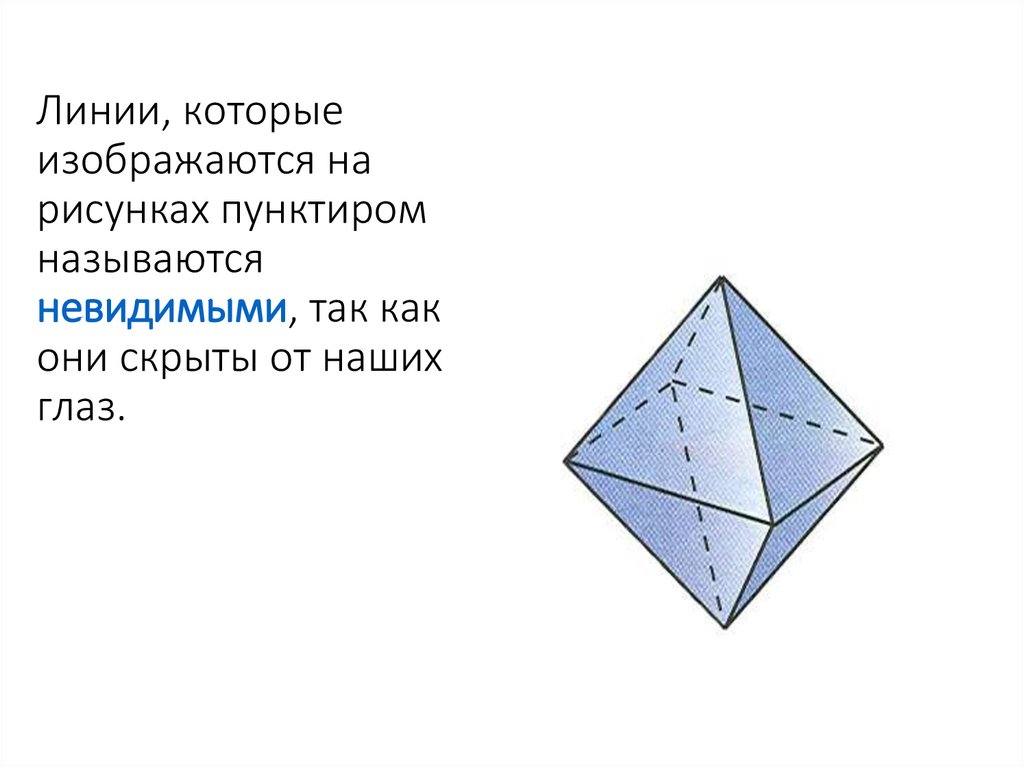
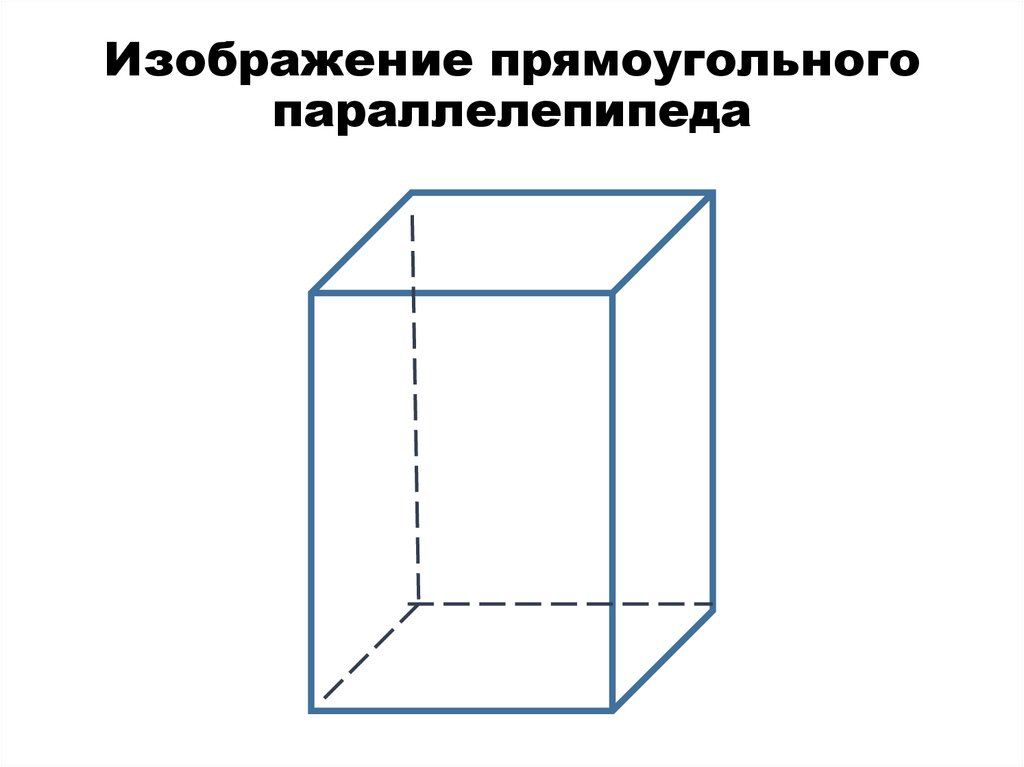
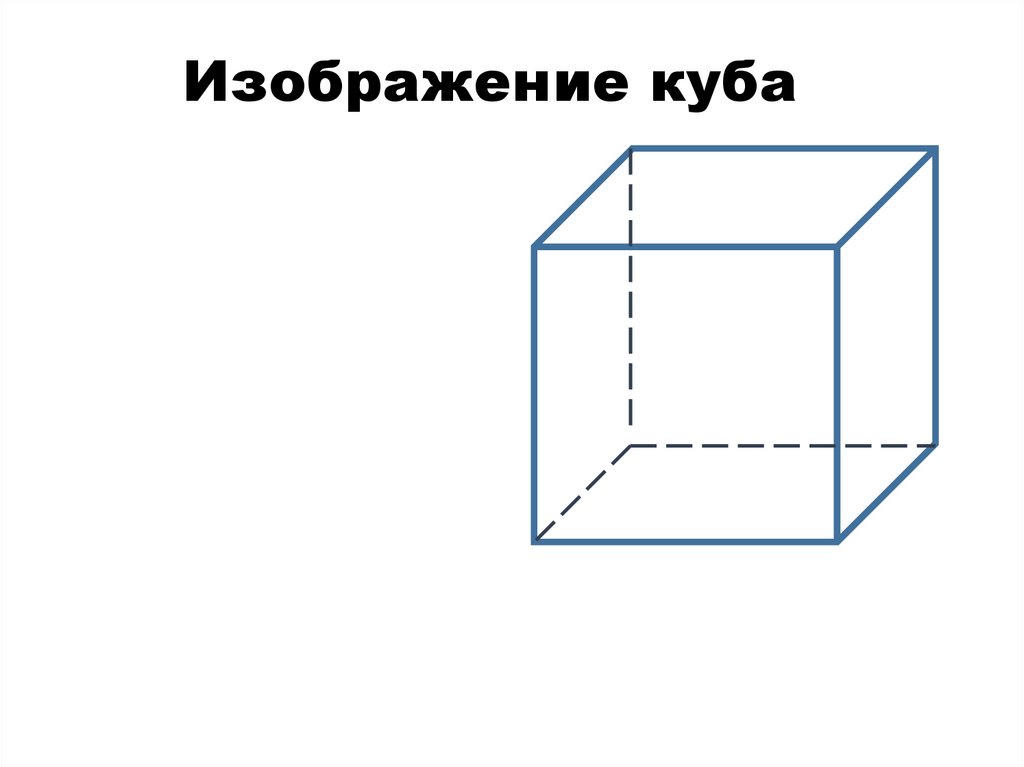
20. Линии, которые изображаются на рисунках пунктиром называются невидимыми, так как они скрыты от наших глаз.
21.
22. Параллелепипед в нашей жизни
Окружающие нас предметы имеют формупрямоугольного параллелепипеда.
23.
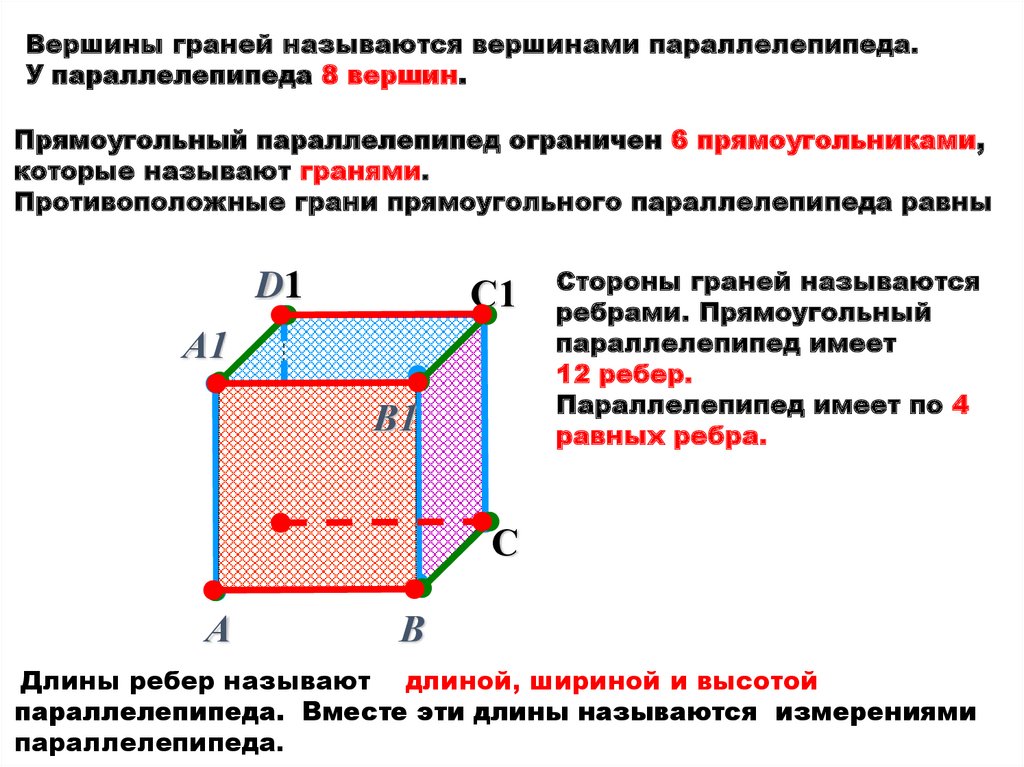
Вершины граней называются вершинами параллелепипеда.У параллелепипеда 8 вершин.
Прямоугольный параллелепипед ограничен 6 прямоугольниками,
которые называют гранями.
Противоположные грани прямоугольного параллелепипеда равны
D1
С1
А1
В1
D
А
Стороны граней называются
ребрами. Прямоугольный
параллелепипед имеет
12 ребер.
Параллелепипед имеет по 4
равных ребра.
С
В
Длины ребер называют длиной, шириной и высотой
параллелепипеда. Вместе эти длины называются измерениями
параллелепипеда.
24. Изображение прямоугольного параллелепипеда
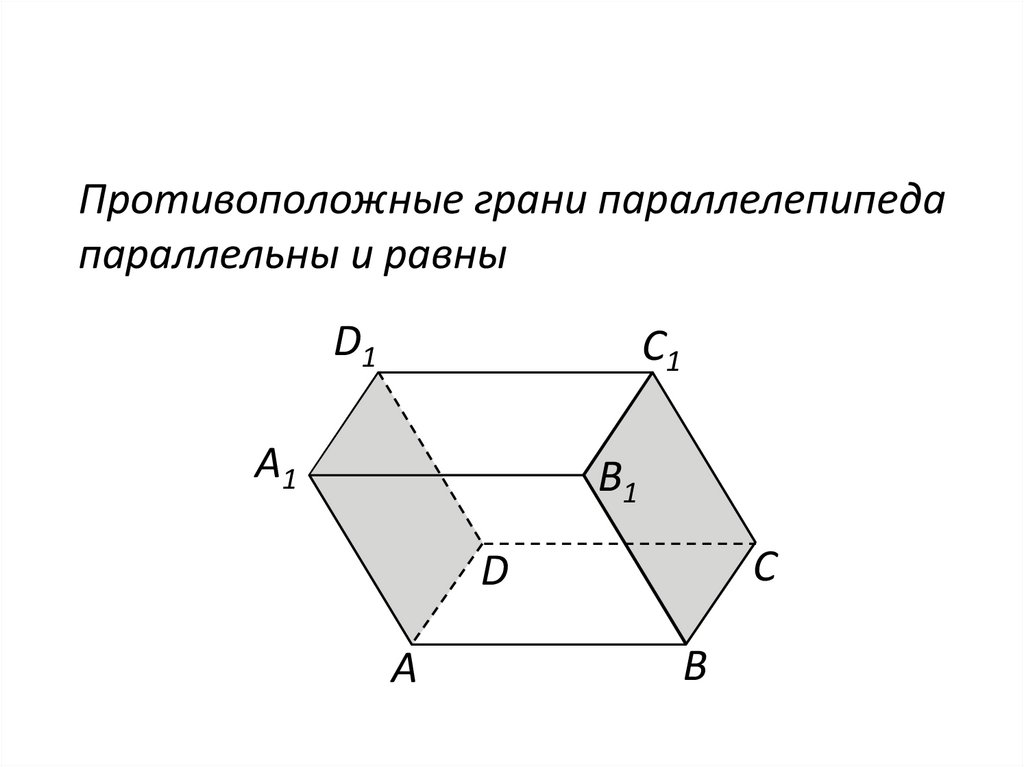
25.
Противоположные грани параллелепипедапараллельны и равны
D1
C1
А1
B1
С
D
А
В
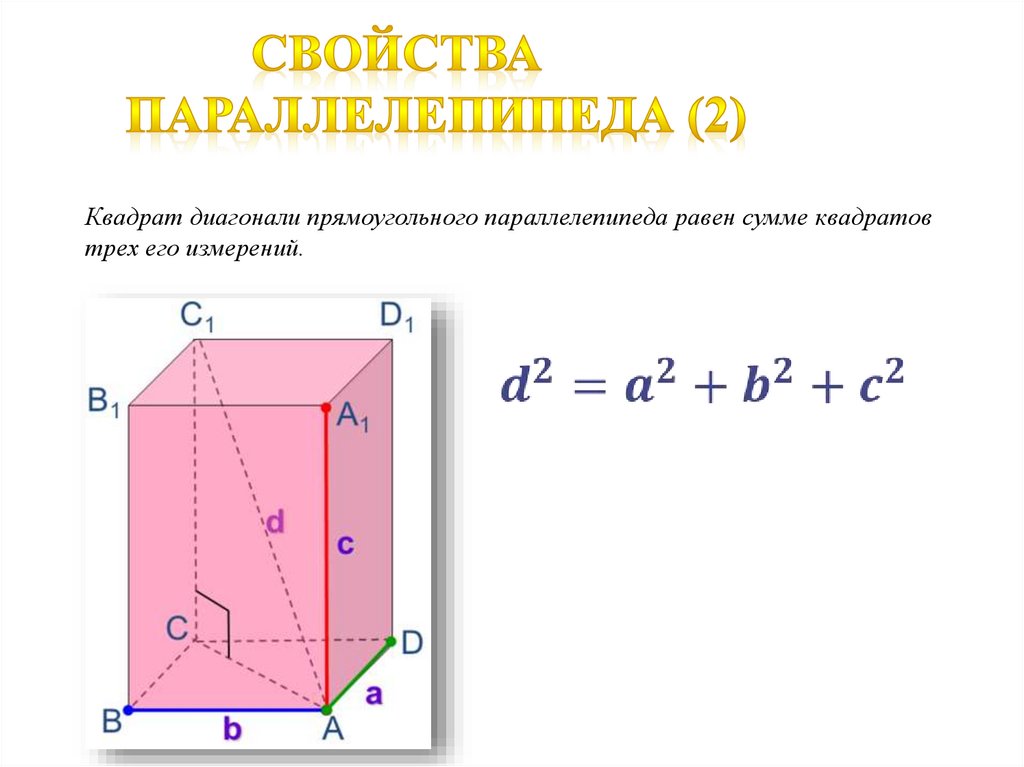
26.
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратовтрех его измерений.
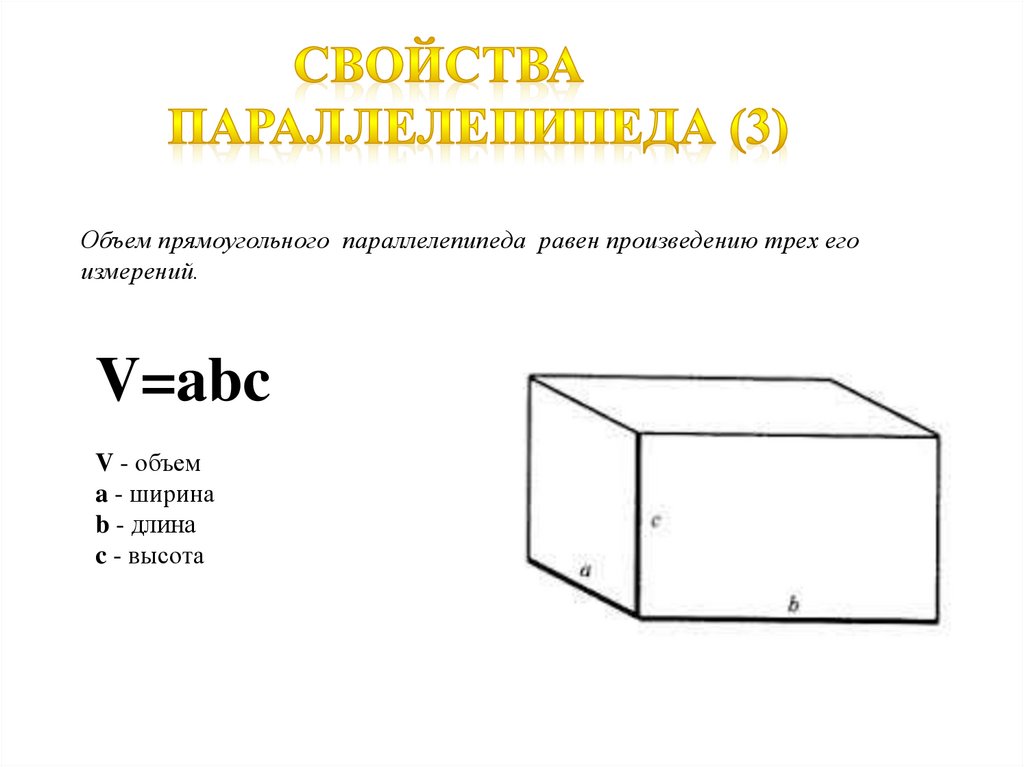
27.
Объем прямоугольного параллелепипеда равен произведению трех егоизмерений.
V=abc
V - объем
a - ширина
b - длина
c - высота
28.
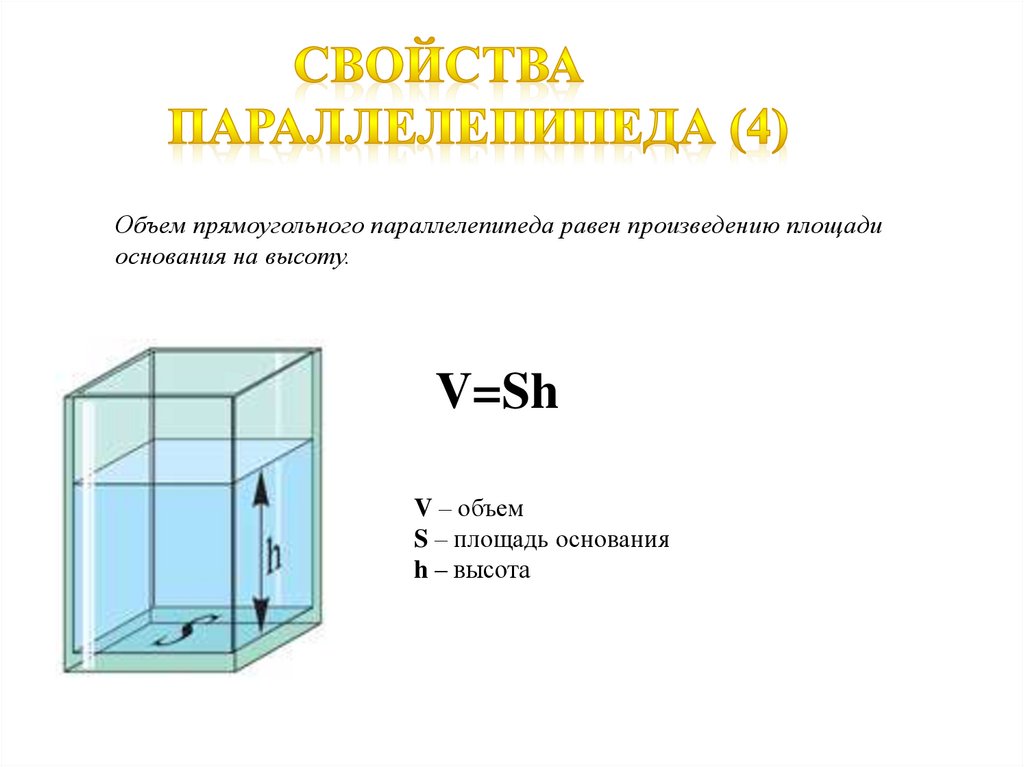
Объем прямоугольного параллелепипеда равен произведению площадиоснования на высоту.
V=Sh
V – объем
S – площадь основания
h – высота
29.
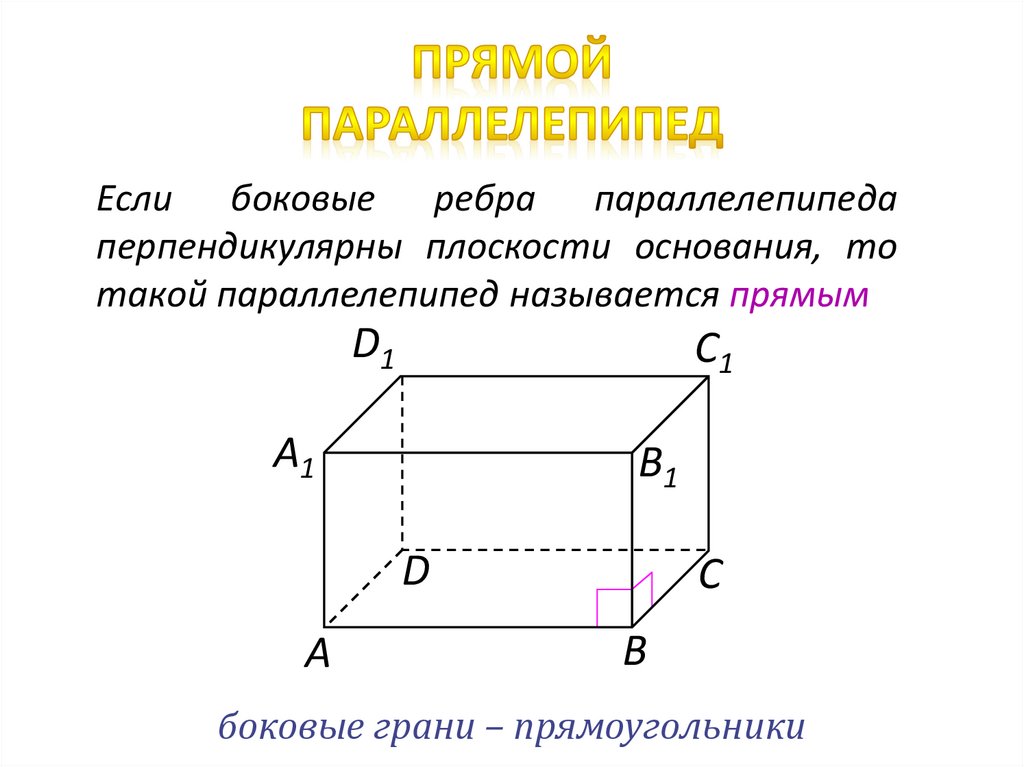
Если боковые ребра параллелепипедаперпендикулярны плоскости основания, то
такой параллелепипед называется прямым
D1
C1
А1
B1
D
А
С
В
боковые грани – прямоугольники
30.
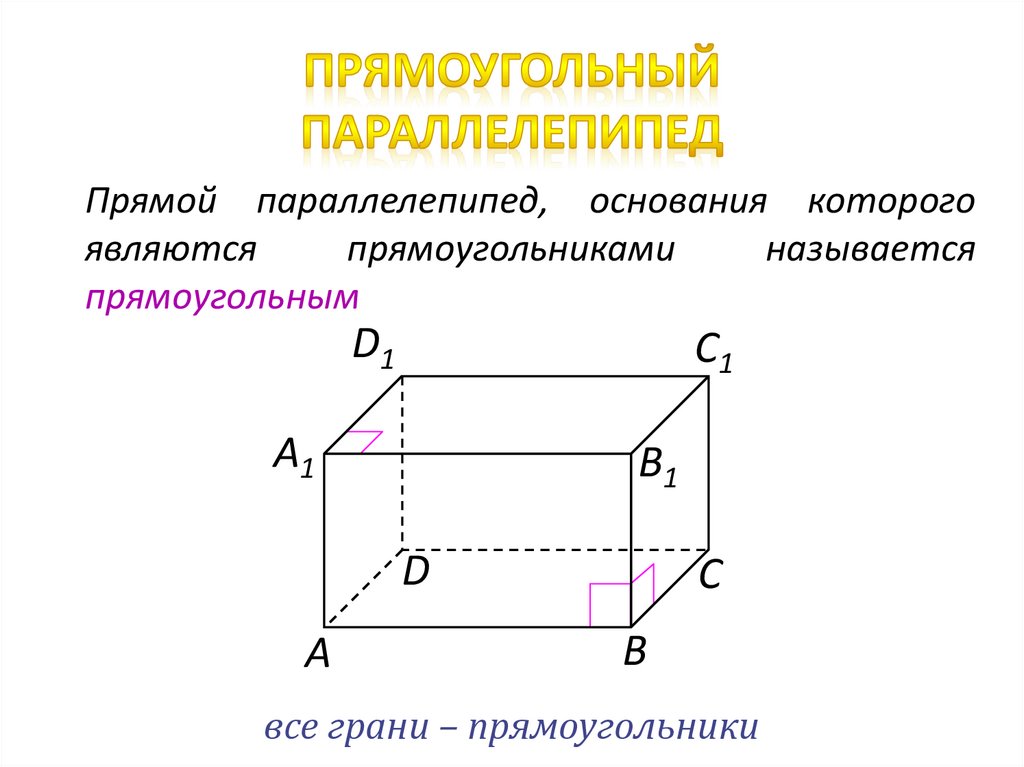
Прямой параллелепипед, основания которогоявляются
прямоугольниками
называется
прямоугольным
D1
C1
А1
B1
D
А
С
В
все грани – прямоугольники
31.
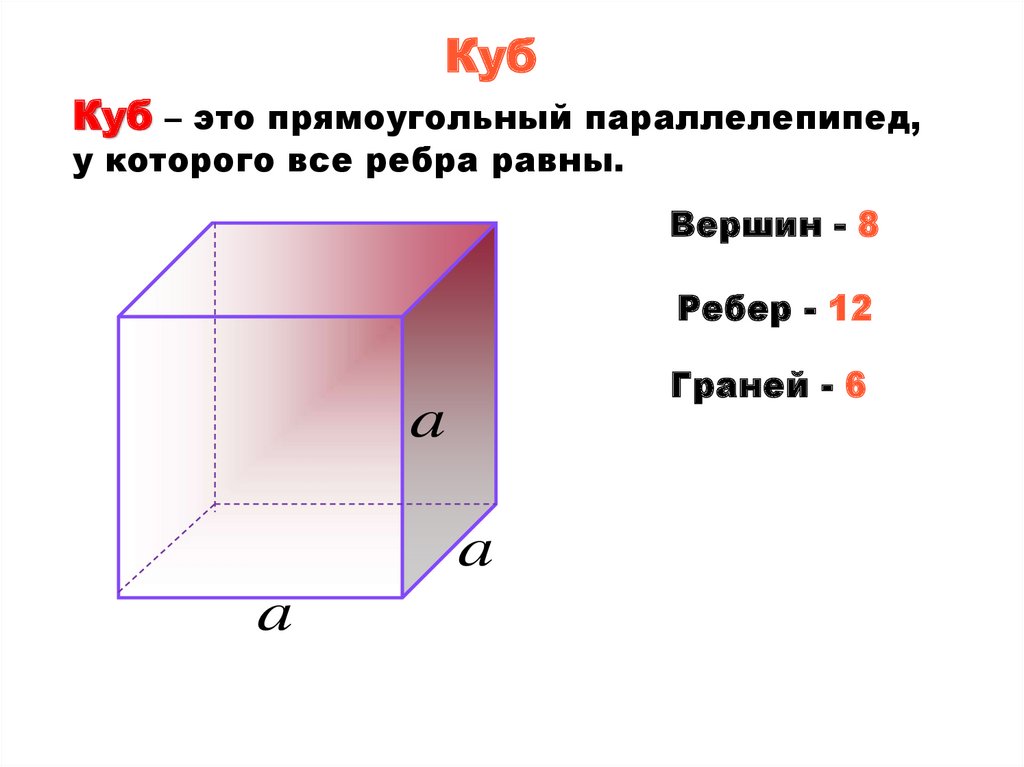
КубКуб – это прямоугольный параллелепипед,
у которого все ребра равны.
Вершин - 8
Ребер - 12
Граней - 6
a
a
a
32.
Прямоугольный параллелепипед, все граникоторого – равные квадраты называется кубом
d
a
a
d2 = 3a2
a
все грани – равные квадраты
33.
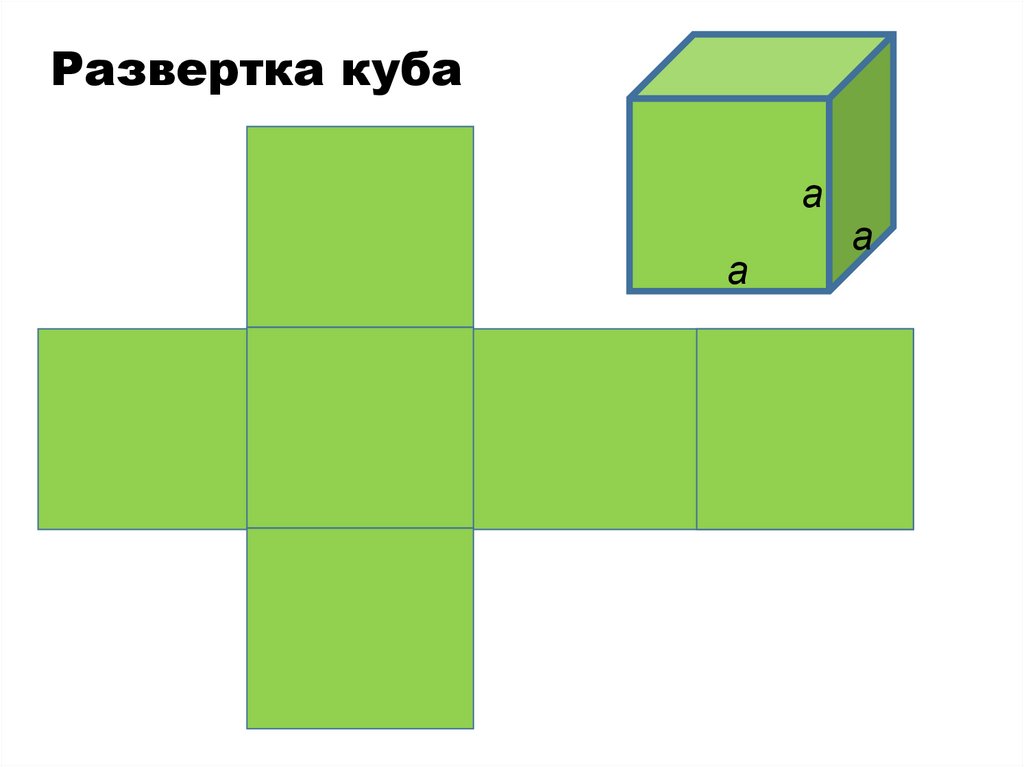
Изображение куба34. Развертка куба
аа
а
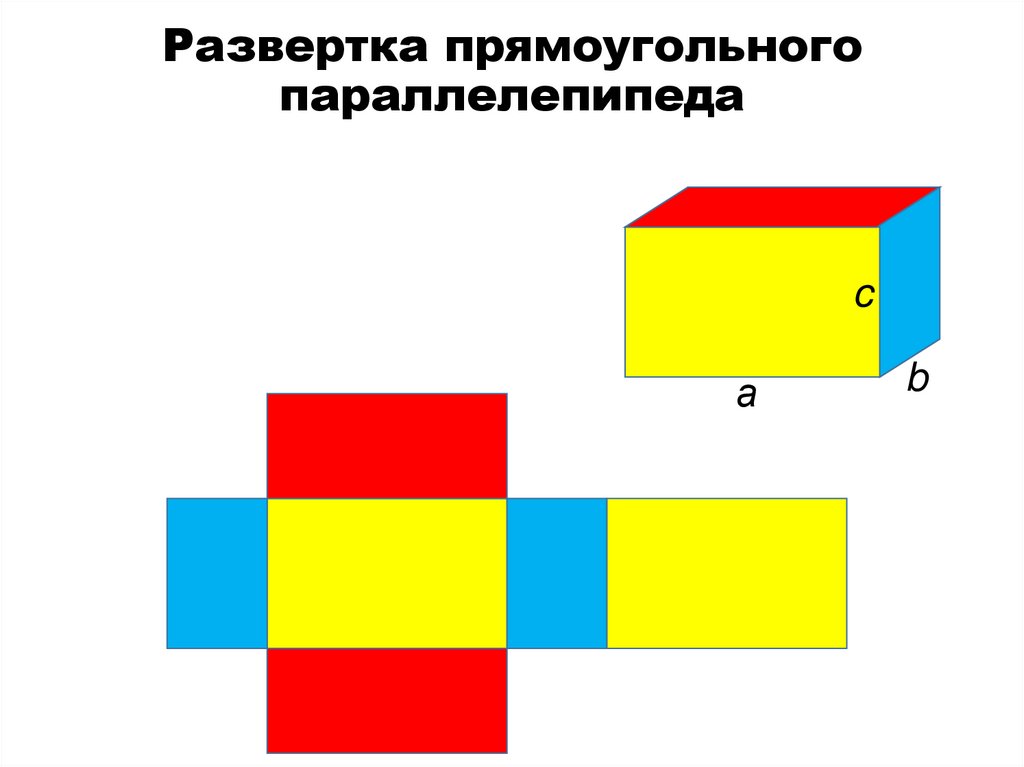
35. Развертка прямоугольного параллелепипеда
cа
b
36.
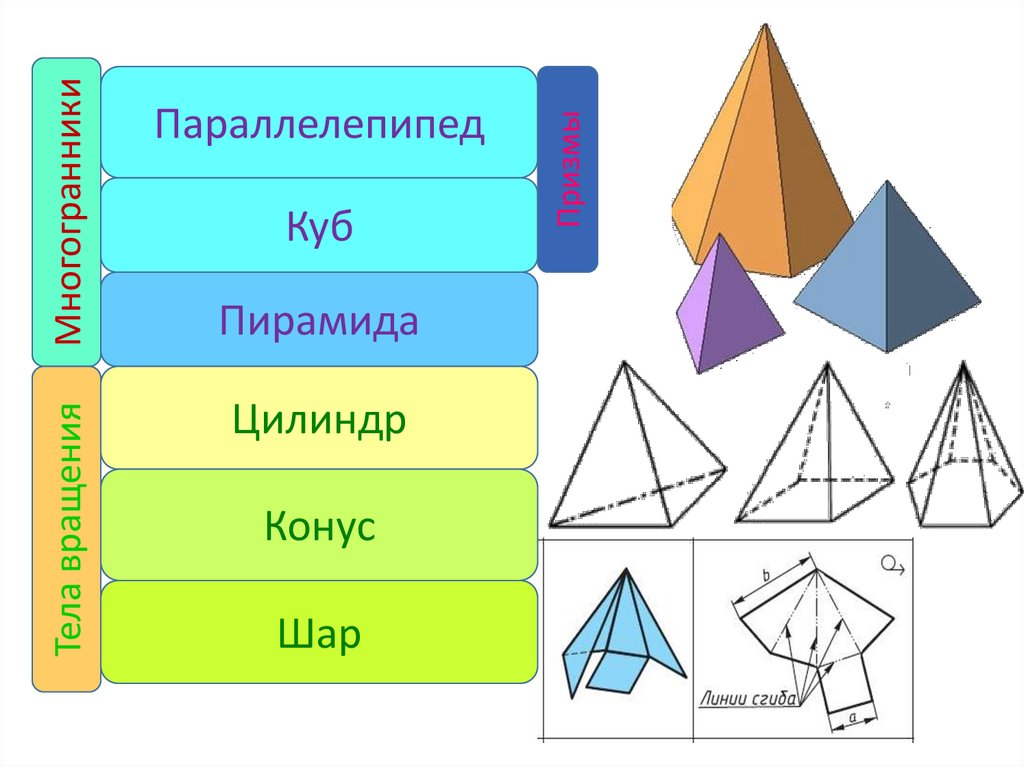
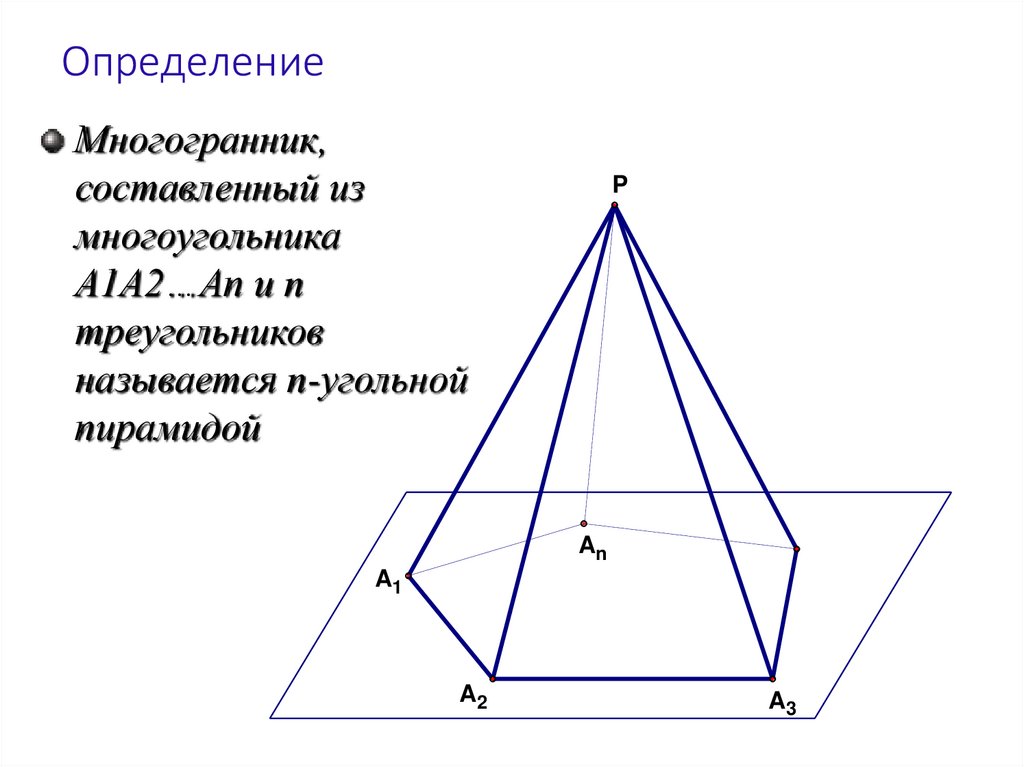
ПИРАМИДА37. Определение
Многогранник,составленный из
многоугольника
A1A2…An и n
треугольников
называется n-угольной
пирамидой
P
An
A1
A2
A3
38.
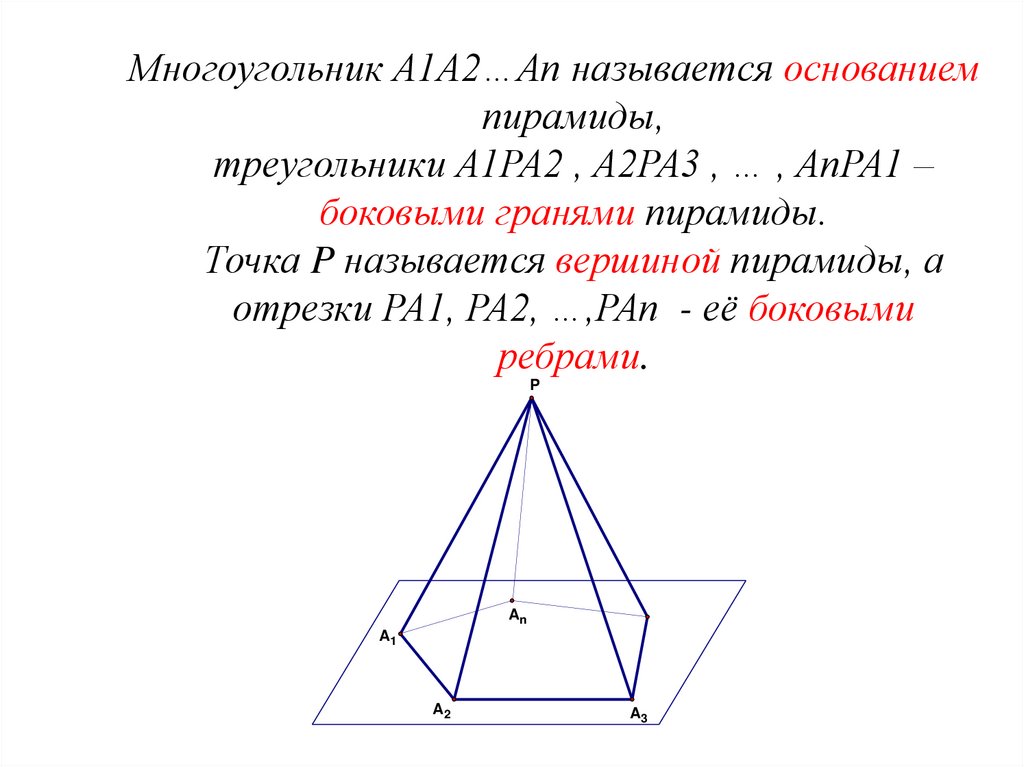
Многоугольник A1A2…An называется основаниемпирамиды,
треугольники A1PA2 , A2PA3 , … , AnPA1 –
боковыми гранями пирамиды.
Точка P называется вершиной пирамиды, а
отрезки PA1, PA2, …,PAn - её боковыми
ребрами.
P
An
A1
A2
A3
39.
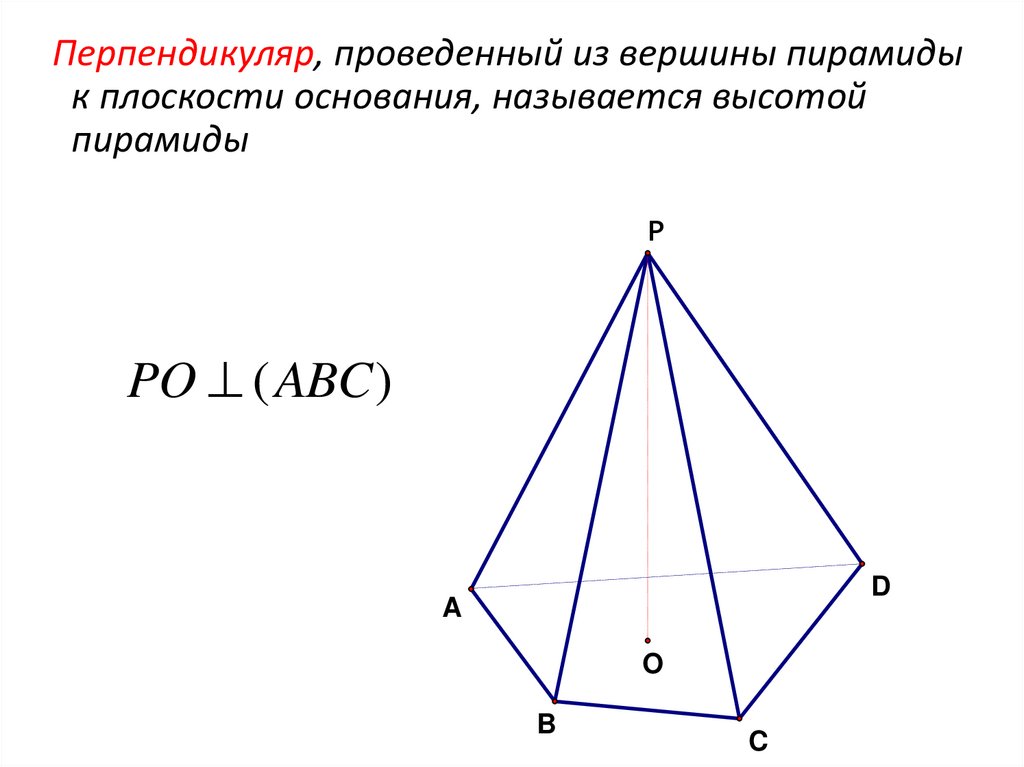
Перпендикуляр, проведенный из вершины пирамидык плоскости основания, называется высотой
пирамиды
P
PO ( ABC )
D
A
O
B
C
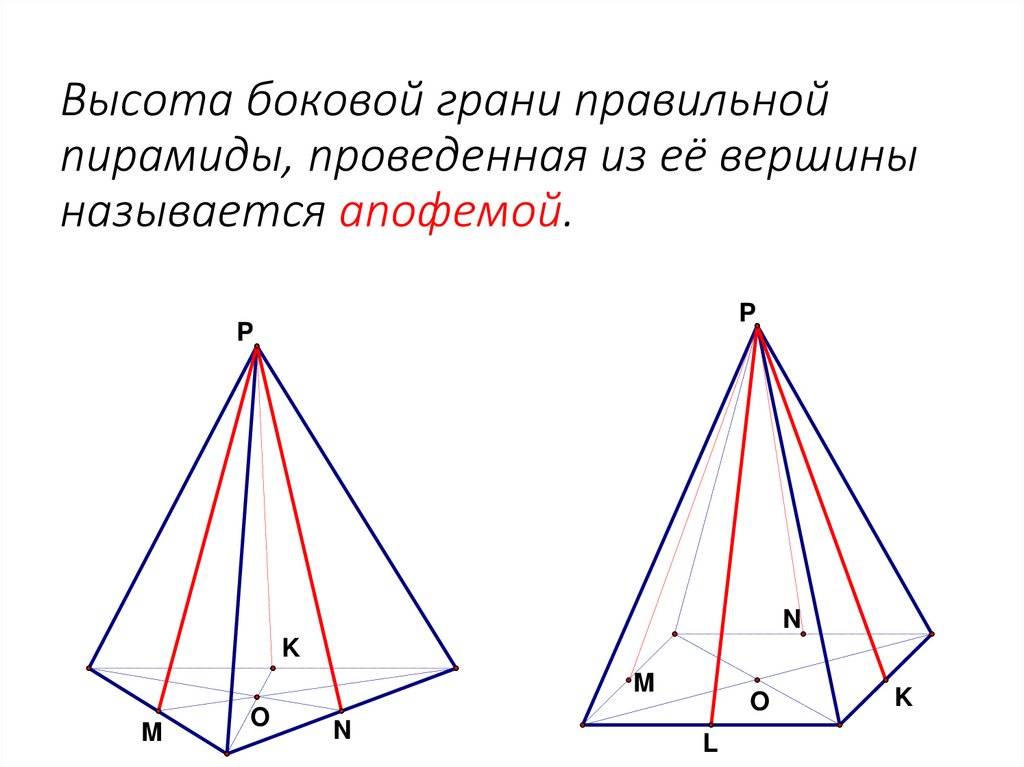
40. Высота боковой грани правильной пирамиды, проведенная из её вершины называется апофемой.
PP
N
K
M
M
O
N
O
L
K
41.
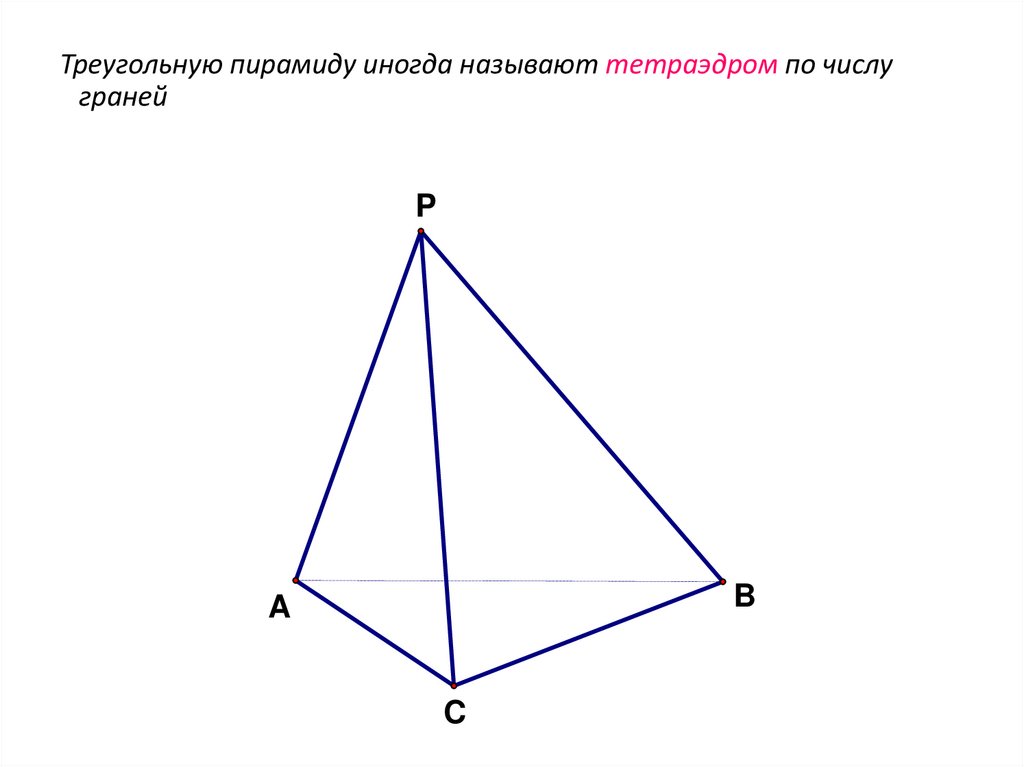
Треугольную пирамиду иногда называют тетраэдром по числуграней
P
B
A
C













 mathematics
mathematics








