В мире многогранников (11 класс)

1.

Подготовил:
ученик 11 «А» класса
Кусаинов Алмаз

2. Цели проекта:

Познакомиться с историей развития
теории многогранников;
Изучить многообразие многогранников,
их использование человеком.

3.

Первые упоминания о многогранниках известны
еще у египтян и вавилонян за 3000 лет до нашей эры. В
тоже время теория многогранников – современный
раздел математики. Она имеет большое значение не
только для теоретических исследований по геометрии,
но и для практических приложений в других разделах
математики.
Многогранники интересны и сами по себе. Они
выделяются необычными свойствами и имеют красивые
формы, например правильные, полуправильные и
звёздчатые многогранники. Они обладают богатой
историей, которая связана с такими знаменитыми
учёными древности, как Пифагор, Евклид, Архимед.
Формы многогранников находят широкое
применение в конструировании сложных и красивых
многогранных поверхностей, которые используются в
реальных архитектурных проектах.

4.

Геометрия как теоретическая наука стала
складываться в Древней Греции в период с VΙΙ по ΙΙΙ
век до н.э. Известны, правда, и более ранние сведения
о геометрии, в частности о многогранниках, но это
были отдельные разрозненные факты.
Так, например, многогранники были известны в
Древнем Египте и Вавилоне. Достаточно вспомнить
знаменитые египетские пирамиды и самую известную
из них – пирамиду Хеопса. Это правильная пирамида,
в основании которой квадрат со стороной 233м и
высота которой достигает 146,5м.
Над её сооружением трудились ежедневно около
100000 человек в течение 20 лет.

5.

В древней Греции основную роль в развитии геометрии
сыграли так называемые философские школы, самыми
известными были школы Фалеса, Пифагора, Платона,
Александрийская и др.
Фалес (635—548 гг. до н. э.) из Милета определил высоту
предмета по её тени. Он измерял высоту пирамиды
«наблюдая тень пирамиды в тот момент, когда наша
тень имеет такую же длину, как и мы сами».
В V веке до нашей эры ведущая роль в развитии
математики принадлежит Пифагору (570— 470 гг. до н.
э.).
Пифагорейцы занимались изучением правильных
многоугольников. Именно школе Пифагора
приписывают открытие существования пяти типов
правильных выпуклых многогранников, которые
использовались для философских космологических
теорий. Согласно этим теориям элементы первоосновы
бытия: огонь, земля, воздух, вода
имеют форму правильных многогранников,
соответственно правильного тетраэдра, куба, октаэдра и
икосаэдр (рис. 1). Форму правильного додекаэдра (рис.
2) имела вся Вселенная.

6.

Более поздняя школа Александрийская. В 323 году до нашей эры
началась
эпоха эллинизма, которая дала миру трех знаменитых ученых:
Евклида, Архимеда, Аполлония.
Евклид является центральной фигурой этого периода, а вместе с
тем и всей древнегреческой математической науки. Из работ,
написанных Евклидом, главным произведением являются
«Начала». Оно состоит из 13 книг. Книги ХI—ХIΙΙ посвящены
стереометрии. В них излагаются начала стереометрии,
определяются отношения площадей кругов, объемов пирамид и
других тел, излагается теория правильных выпуклых
многогранников,
Кроме Евклида, крупным ученым эпохи эллинизма был Архимед
(287— 212 гг. до н. э.),
Архимед внес существенный вклад в математику. Ему
принадлежат теоремы о площадях плоских фигур, объемах тел.
Вслед за Евклидом Архимед занимался изучением правильных
многогранников.

7.

Еще одним крупным ученым той эпохи, занимавшимся
изучением многогранников, был Аполлоний (260— 170 гг. до н.
э.). Ему принадлежит теорема о том, что отношение объемов
октаэдра и икосаэдра равно отношению площадей их
поверхностей (задача
Аполлония).
Итак, к началу нашей эры ученые древности накопили
достаточно сведений по теории многогранников. Они описали
комбинаторные свойства (связанные с количеством граней,
вершин, ребер) основных простейших выпуклых
многогранников — призм, пирамид, правильных
многогранников, знали метрические свойства этих
многогранников, в том числе умели вычислять объем пирамиды,
применяя метод исчерпывания, использовали многогранники в
строительстве и архитектуре.

8.

Нас окружает множество предметов. Они отличаются формой,
размерами. материалом. из которого изготовлены, окраской.
Разных людей интересуют разные качества этих предметов.
Математиков интересуют форма предметов и их размеры.
Изображенные на рисунке мячи имеют форму шара, хотя все
они разных размеров. Многие небесные тела имеют форму,
близкую к форме шара. Стакан и карандаш на рисунке имеют
форму цилиндра.

9.

Формы предметов очень разнообразны и не для всякой формы
имеется специальное название.
Так как математики изучают не сами предметы, а их формы, то
вместо предметов они рассматривают геометрические тела:
цилиндр, шар, конус и т.д. Названия многих геометрических тел
идут из глубокой древности, причем произошли они от
соответствующих предметов. Например, из древней Греции термины
конус (conus — предмет, которым затыкали бочку), “пирамида”
(pura — огонь, костер), “цилиндр” (cylindrus — валик).
Интересный факт: все геометрические тела, кроме шара,
называются словами иностранного происхождения. А линии и их
части называются чисто русскими словами: прямая, отрезок,
ломаная, луч, треугольник, многоугольник

10.

Вспомним, что замкнутая линия разбивает
плоскость на две части: внутреннюю и
внешнюю. Эти области отделяются друг от
друга самой данной линией, которая для
каждой из этих областей является границей.
Точно так же и каждое геометрическое тело,
которое мы рассматриваем, имёет
внутреннюю и внешнюю области.
Внутренняя и внешняя области
геометрического тела отделены друг от
друга поверхностью этого тела.
Поверхность шара называется сферой, а для
поверхностей других геометрических тел
специальных терминов нет, говорят просто:
поверхность конуса, поверхность куба и т.д.

11.

Среди множества разнообразных геометрических тел есть большая группа
многогранников.
МНОГОГРАННИК – это такое тело, поверхность которого состоит из
конечного числа плоских многоугольников.
На рисунке изображены различные многогранники.
При всем их различии многогранники имеют ряд общих свойств.
Поверхность многогранника состоит из многоугольников.
Каждый из этих многоугольников называют гранью многогранника.
Вершины этих многоугольников являются также и вершинами многогранника, а
стороны многоугольников — ребрами многогранника.
Обратите внимание на то, что у многоугольника число вершин равно числу
сторон, а у многогранника число вершин и число граней необязательно одинаково.

12. «ИДЕАЛЬНЫЕ», «КОСМИЧЕСКИЕ» ФИГУРЫ – ТЕЛА ПЛАТОНА

Какие правильные многогранники вы знаете? Сколько их? На рисунке
представлены все пять видов правильных многогранников: самый простой
— тетраэдр (рис. а), куб, или гексаэдр (рис. 6), октаэдр (рис. в), додекаэдр
(рис. г), икосаэдр (рис. д).
Почему правильные многогранники получили такие имена? Это связано
с числом их граней. Так, тетраэдр имеет четыре грани, в переводе с
греческого «тетра» — четыре, «эдрон» — грань, вот и получается
четырехгранник - тетраэдр. Гексаэдр (куб) имеет шесть граней, «гекса» —
шесть; октаэдр — восьмигранник, «окто» — восемь; додекаэдр
двенадцатигранник, «додека» — двенадцать; наконец, икосаэдр имеет
двадцать граней, «икоси» - двадцать.

13. Какой многогранник называется правильным?

Чтобы ответить на этот вопрос, давайте сначала
перечислим свойства правильных многогранников. Итак:
1. Все ребра равны.
2. Все плоские углы равны.
З. Все грани равные, правильные многоугольники.
4. Все двугранные углы равна.
5. Все многогранные углы равны.
6. Все многогранные углы имеют одно и то же число
граней, и в каждой вершине сходится одно и то же число
ребер.

14.

Отсюда следуют определения правильных
многогранников:
ОПРЕДЕЛЕНИЕ 1. Правильным многогранником
называется многогранник, у которого все грани –
правильные равные многоугольники и все двугранные
углы равны.
ОПРЕДЕЛЕНИЕ 2. Выпуклый многогранник называется
правильным, если его грани являются правильными
многоугольниками с одни и тем же числом сторон и в
каждой вершине многогранника сходится одно и то же
число рёбер.

15. ИЗОБРАЖЕНИЕ ГЕОМЕТРИЧЕСКИХ ТЕЛ

С давних пор люди пытались изобразить объемные тела на плоскости так, чтобы их сразу можно
было отличить от плоских, чтобы чувствовалась глубина пространства. Были разработаны
специальные приемы, позволяющие обмануть зрение. Один из них — перспектива. Простым примером
может служить картина, на которой изображены железнодорожные рельсы: рельсы кажутся
сходящимися в одной точке, что и создает иллюзию объемного изображения.
Посмотрите на рисунок. Здесь изображен многогранник (рис. а). Хорошо видны три его передние
грани, но, не “обойдя его”, невозможно представить себе, как он выглядит сзади.
Представьте себе, что этот многогранник прозрачный (рис. б). Теперь мы видим все его грани, ребра,
вершины. Но изображать многогранник прозрачным не очень удобно. Получается набор линий, как на
рисунке в, в котором трудно разобраться. Глядя на этот рисунок, невозможно понять, как линии
расположены в пространстве.
В геометрии для облегчения восприятия договорились линии, которые скрыты от глаз наблюдателя,
изображать не сплошными, а штриховыми. Тогда наш многогранник мы будем изображать так, как
показано на рисунке г.

16. ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД

Как мы уже знаем, многогранники могут иметь самую различную форму. Среди них
выделяют прямоугольный параллелепипед (рис. 1). Обычный, всем известный кирпич с
точки зрения геометрии является параллелепипедом.
Форму параллелепипеда имеют
спичечные коробки, телевизоры и многие другие предметы, с которыми мы постоянно
встречаемся в нашей жизни. Форму прямоугольного параллелепипеда часто используют
архитекторы при проектировании зданий.
Каждый параллелепипед имеет три измерения: длину, ширину и высоту (рис.2).
У параллелепипеда 8 вершин, 12 ребер, 6 граней. Каждая грань параллелепипеда —
прямоугольник. Противоположные грани параллелепипеда равны.
Среди всех параллелепипедов особую роль играет один, хорошо вам известный — куб.
Куб, — это такой прямоугольный параллелепипед, у которого все ребра равны, поэтому все
его грани — квадраты.
Рис. 2
Рис. 1.

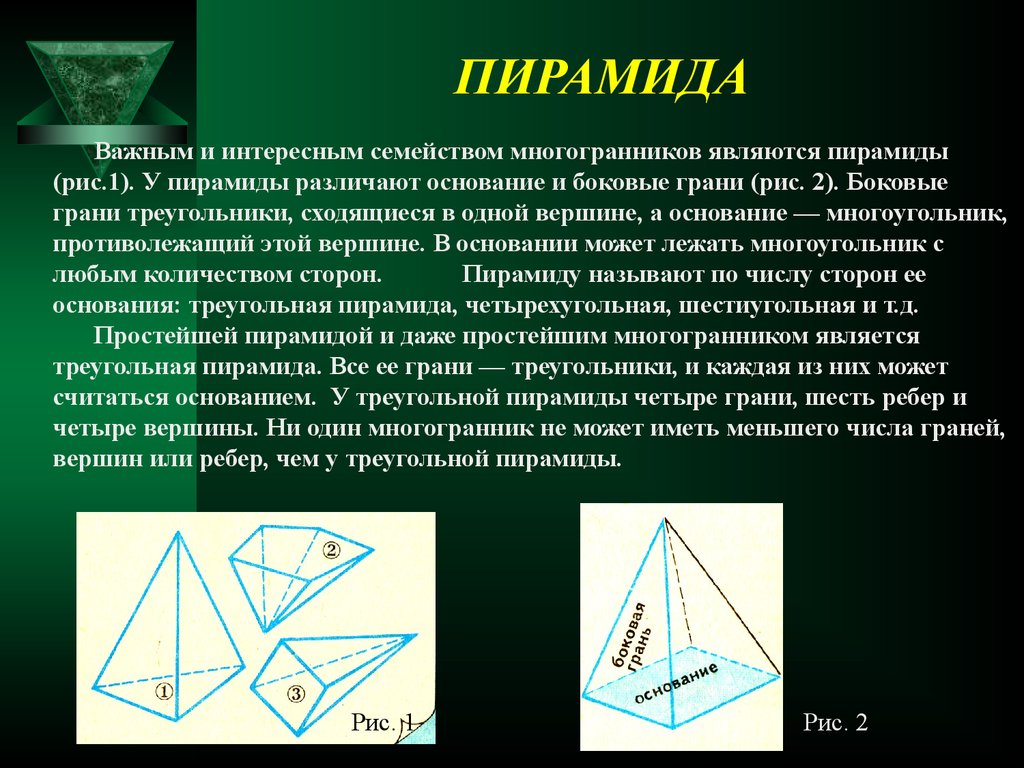
17. ПИРАМИДА

Важным и интересным семейством многогранников являются пирамиды
(рис.1). У пирамиды различают основание и боковые грани (рис. 2). Боковые
грани треугольники, сходящиеся в одной вершине, а основание — многоугольник,
противолежащий этой вершине. В основании может лежать многоугольник с
любым количеством сторон.
Пирамиду называют по числу сторон ее
основания: треугольная пирамида, четырехугольная, шестиугольная и т.д.
Простейшей пирамидой и даже простейшим многогранником является
треугольная пирамида. Все ее грани — треугольники, и каждая из них может
считаться основанием. У треугольной пирамиды четыре грани, шесть ребер и
четыре вершины. Ни один многогранник не может иметь меньшего числа граней,
вершин или ребер, чем у треугольной пирамиды.
Рис. 1.
Рис. 2

18. Развертки

На рисунке 1 изображена некоторая фигура (рис. а). Если ее вырезать из
бумаги и сложить (рис. б), то получится куб (рис. в). И наоборот, Разрезав
поверхность куба по некоторым ребрам, мы можем развернуть ее на плоскости.
При этом мы получим развертку куба.
Если мы хотим сделать из бумаги какой-нибудь многогранник, то его можно
получить следующим образом: начертить на бумаге его развертку, вырезать ее,
свернуть по линиям, соответствующим ребрам многогранника, и склеить. Для
удобства склейки можно по контуру развертки в некоторых местах оставить
узенькие полоски бумаги.
На рисунке 2 дана развертка ромбоусеченного кубооктаэдра. Этот
многогранник состоит из 26 граней, из которых 6 правильных восьмиугольников,
8 правильных шестиугольников и 12 квадратов.
Рис. 1.
Рис. 2

19. Выводы:

В результате работы мы:
познакомились с многообразием
многогранников, их свойствами,
узнали основы теории многогранников,
узнали о применении многогранников
человечеством со времён Древнего мира
по настоящее время.