Математикалық ұғымдарды

1. ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ  «ӨРЛЕУ» БІЛІКТІЛІКТІ АРТТЫРУДЫҢ ҰЛТТЫҚ ОРТАЛЫҒЫ АҚ ФИЛИАЛЫ  БІЛІМ БЕРУ ЖҮЙЕСІНІ

ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ
«ӨРЛЕУ» БІЛІКТІЛІКТІ АРТТЫРУДЫҢ ҰЛТТЫҚ ОРТАЛЫҒЫ АҚ ФИЛИАЛЫ
БІЛІМ БЕРУ ЖҮЙЕСІНІҢ БАСШЫ ЖӘНЕ ҒЫЛЫМИ -ПЕДАГОГИКАЛЫҚ
КАДРЛАР БІЛІКТІЛІГІН АРТТЫРАТЫН РЕСПУБЛИКАЛЫҚ ИНСТИТУТ
ЖОО педагогикалық мамандары оқытушыларының біліктілігін арттыру
БАҒДАРЛАМАСЫ
ПОРТФОЛИО
Мектеп математика курсының логикалық құрылымы пәні.
МАТЕМАТИКАЛЫҚ ҰҒЫМДАРДЫ
АНЫҚТАУДЫҢ ЛОГИКАЛЫҚ ТАЛДАУЫ:
АССОЦИОГРАММАЛЫҚ ТАЛДАУ
Тыңдаушы: Қорқыт Ата атындағы Қызылорда мемлекеттік университеті
“Гуманитарлық-педагогикалық” институты
“Физика және математика” кафедрасының магистрі
Джузбаева Айнур Мнажовна
Оқу мерзімі: 13.05.13 ж – 26.05.13 ж
Портфолио жетекшісі:
филос.ғ.д., доцент Оспанов С.И.
Алматы

2. М А З М Ұ Н Ы:  

М А З М Ұ Н Ы:
• Тыңдаушы туралы ақпарат
• «Математикалық ұғымдарды
анықтаудың логикалық талдауы»
тақырыбын оқытуға инновациялық
әдістерді пайдалану (практикалық сабақ)
• Білім алушының өзіндік жұмысын
ұйымдастыру
• Білімді бағалау жүйесі
• Интерактивті тест
• Аналитикалық есеп

3. Тыңдаушы туралы ақпарат:

Джузбаева Айнур
Мнажовна
Білімі: 1998 – 2002 жылдар аралығында Қарағанды
мемлекеттік
университетінде
“Математика“
мамандығының “Математик. Оқытушы” біліктілігі
бойынша білім алған. 2002-2004 жылдар аралығында
аталған
мамандық
бойынша
магистратураны
тәмамдаған.
Еңбек өтілі: 2002-2004жылдар аралығында Қарағанды
қаласындағы №41 мектебінің математика пәнінің
мұғалімі, 2004-2005 жылдар аралығында ҚарМУ –нің
математика факультетіндегі Т.Ғ.Мұстафин атындағы
“алгебра, геометрия және математикалық логика”
кафедрасының оқытушысы, 2005 жылдан бастап
ҚызМУ-де оқытушы.
Жүргізетін пәндері: Алгебра және сандар теориясы,
мектеп математика курсының логикалық құрылымы,
математикадан кластан тыс жұмыстар және т.б.

4. Сабақтың жоспары:

1. Математиканың логикалық құрылымы
туралы түсінік.
2. Математикалық ұғымдарды анықтау.
3. Математикалық ұғымның негізгі
сипаттамалары.
4. Математикалық ұғымдарды
классификациялаудың шарттары.
5. Мысалдар.

5. Практикалық сабақтың тақырыбы:

“Математикалық ұғымдарды анықтаудың
логикалық талдауы”
SMART мақсаты: Студент 1 оқу сағаты
ішінде математикалық ұғым анықтамасының
логикалық
талдауын
ұғымның
елеулі
белгілері арқылы жасауды үйрену керек.

6. М А Қ С А Т Ы:

• Математикалық ұғымдар туралы
білімдерін жүйелей түсіндіру.
• Оқушылардың конструктивті
ойлауын дамыту.
• Оқушыларды ізденімпаздыққа,
жауапкершілікке, ұйымшылдыққа,
іскерлікке тәрбиелеу.

7. 1. Математикалық білім беру төмендегі мәселелерді қамтитын күрделі процесс:

а) Математикалық
фактілер мен идеяларды
меңгерту;
ә) Математикалық біліктер мен дағдыларды
қалыптастыру;
б) Математикалық ойлауды дамыту.

8. АССОЦИОГРАММА ӘДІСІ НЕМЕСЕ «MIND MAP» - АҚЫЛ (ОЙ) КАРТАСЫ

Негізін салушы ағылшын ғалымы
Тони Бузан (1970)

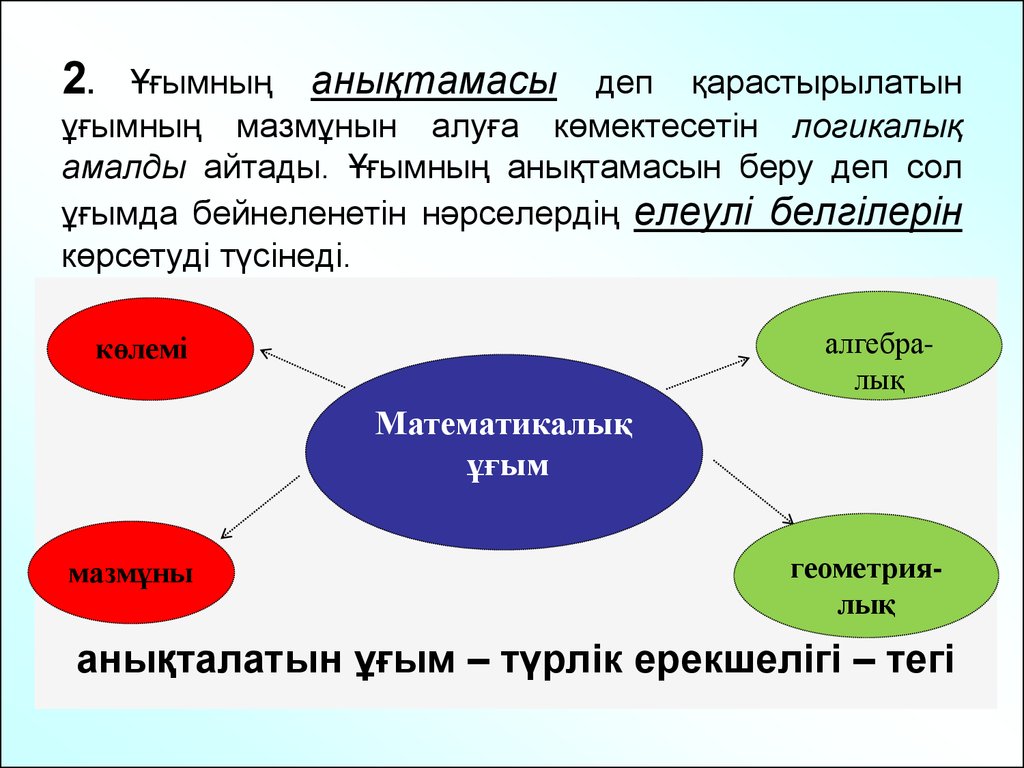
9. 2. Ұғымның анықтамасы деп қарастырылатын ұғымның мазмұнын алуға көмектесетін логикалық амалды айтады. Ұғымның анықтамасын беру деп сол ұғ

Ұғымның анықтамасы деп қарастырылатын
ұғымның мазмұнын алуға көмектесетін логикалық
амалды айтады. Ұғымның анықтамасын беру деп сол
ұғымда бейнеленетін нәрселердің елеулі белгілерін
көрсетуді түсінеді.
2.
алгебралық
көлемі
Математикалық
ұғым
мазмұны
геометриялық
анықталатын ұғым – түрлік ерекшелігі – тегі

10. Теориялық-анатомиялық негізі

Егер қалыпты жағдайда мидың сол жақ
жартысы ғана ойлау орталығы болса, онда
ассоциативтік әдіс соның екі
жартысын да ойлау үдерісіне бірде
қатыстыруды мақсат етеді.

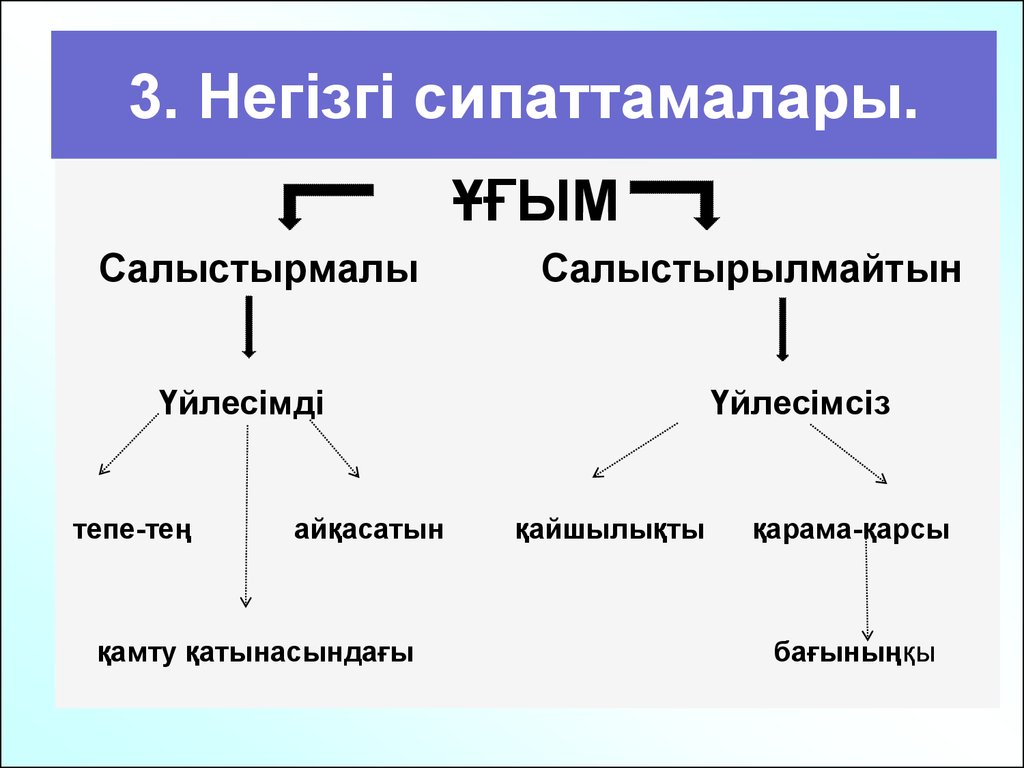
11. 3. Негізгі сипаттамалары.

ҰҒЫМ
Салыстырмалы
Салыстырылмайтын
Үйлесімді
тепе-тең
айқасатын
қамту қатынасындағы
Үйлесімсіз
қайшылықты
қарама-қарсы
бағыныңқы

12. Мидың сол жақ жартышары табиғи –жағдайында:

- зерделі ойлау қабілетіне,
- абстракциялық ойлауға,
- белсенді болуға,
- проблема шешуге,
- өзін сыни бақылап, бағалауға жауапты.

13. 4. Математикалық ұғымдарды классификациялаудың шарттары:

• 1. Бөлу негізі біріңғай болуы керек.
• 2. Бөлу өлшемдес болуы тиіс.
• 3. Бөлу мүшелерінің әрқайсысы
басқаларын қоспауы тиіс.
• 4. Бөлу үзіліссіз болуы керек.

14. Дидактикалық біліктерді ірілендіру технологиясы.

Әдістемесі:
• Бір мезгілде тура және кері амалдар
мен операцияларды меңгерту;
• Өзара қарама-қайшы ұғымдарды
салыстыру;
• Тұтас және қарама-қайшы ұғымдарды
сәйкестендіру;
• Амалдардың орындалу тәртібін реттеу.

15. Параллелепипед

SS
?
1.
А
В
2.
С
3.
4.
5.

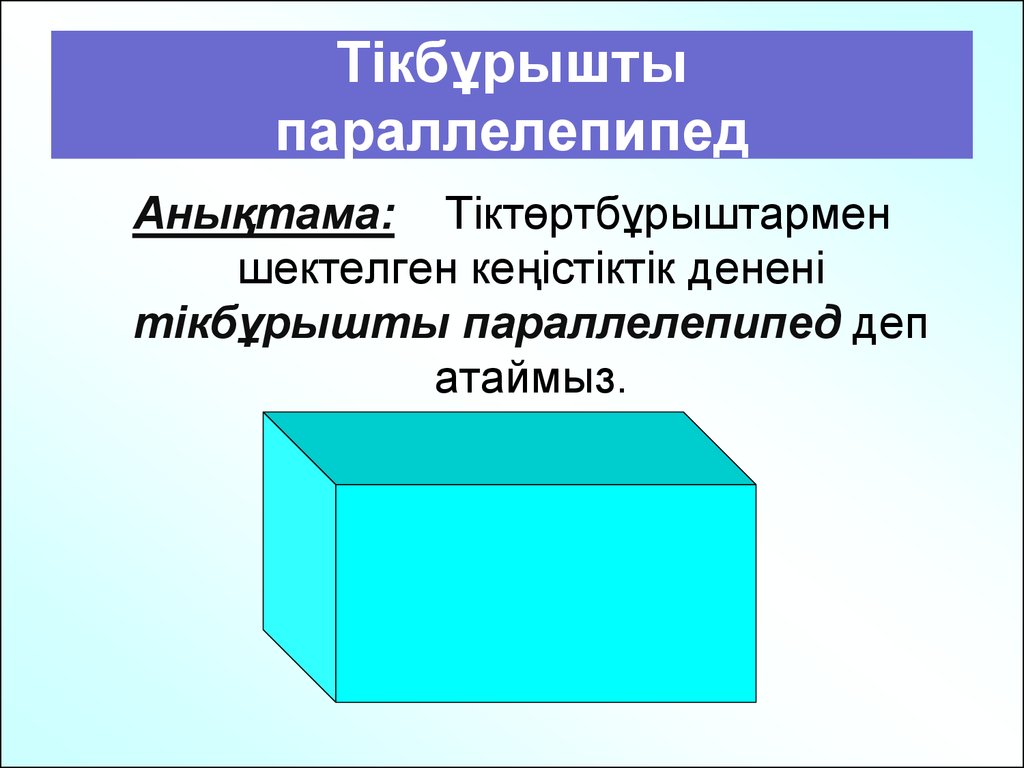
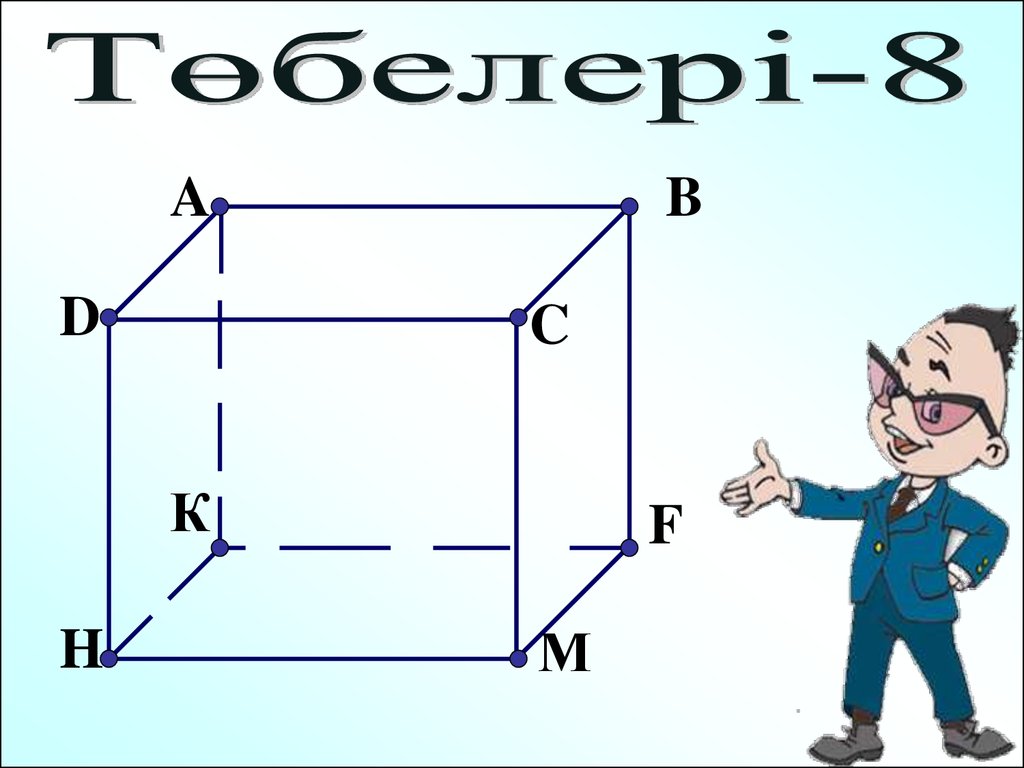
16. Тікбұрышты параллелепипед

Анықтама: Тіктөртбұрыштармен
шектелген кеңістіктік денені
тікбұрышты параллелепипед деп
атаймыз.

17.

A
D
B
C
К
H
F
М

18.

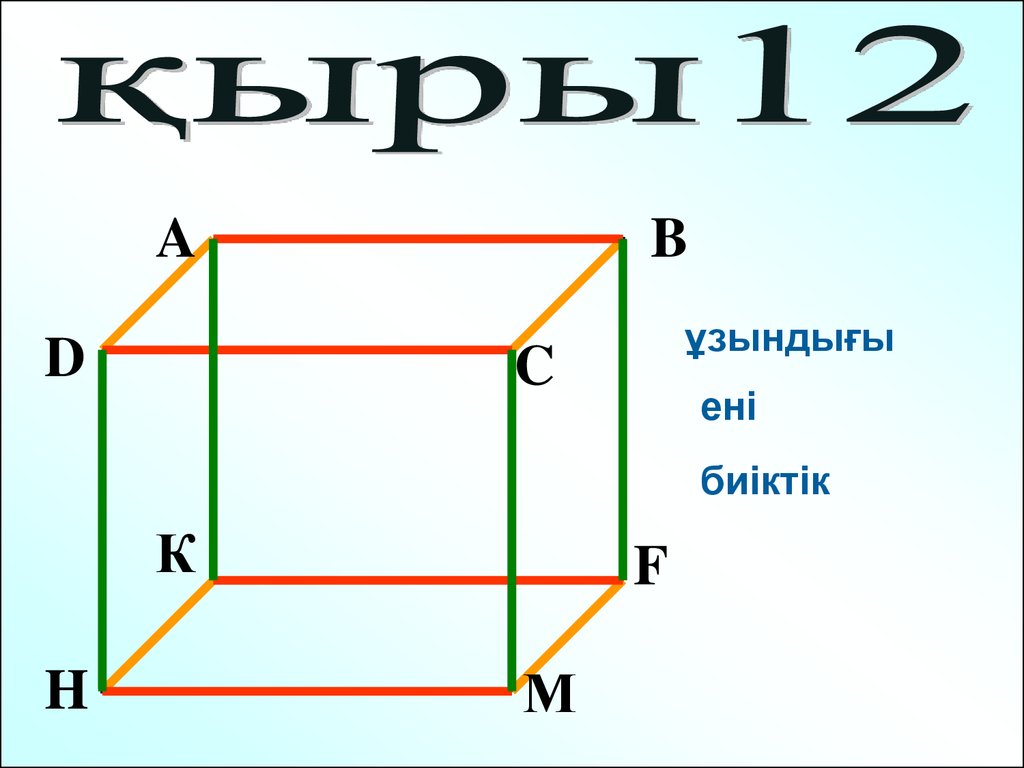
A
D
B
ұзындығы
C
ені
биіктік
К
H
F
М

19.

Тіктөртбұрыштар
Қарама қарсы
жақтары тең !

20.

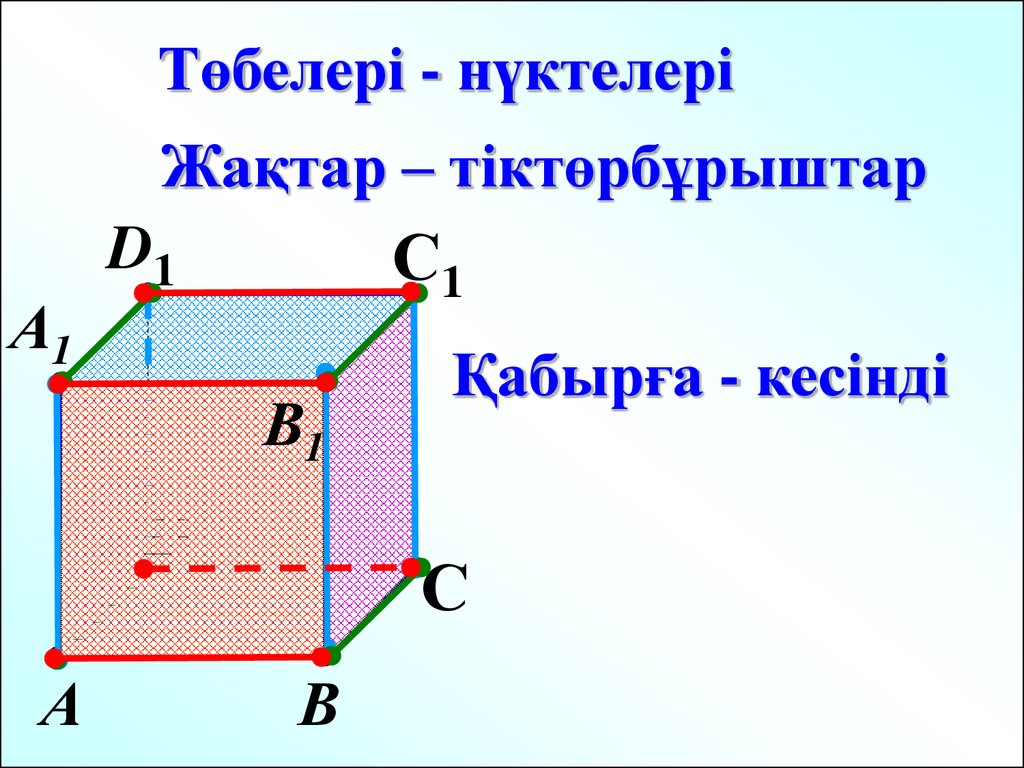
Төбелері - нүктелері
Жақтар – тіктөрбұрыштар
А1
С1
D1
В1
D
А
Қабырға - кесінді
С
В

21.

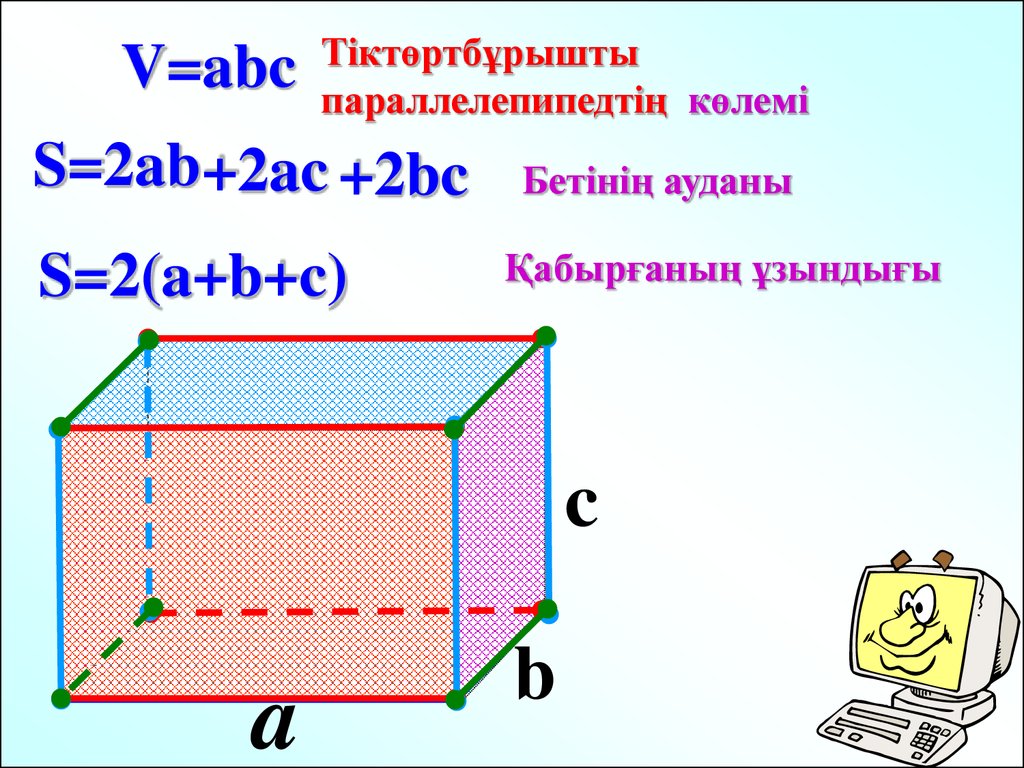
V=abc
Тіктөртбұрышты
параллелепипедтің көлемі
S=2ab+2ac +2bc
S=2(a+b+c)
Бетінің ауданы
Қабырғаның ұзындығы
c
a
b

22.

3
V=a
S=6a2
Кубтің көлемі
Куб бетінің ауданы
L=12a
a
a
a
Куб
қабырғаларының
ұзындығы

23.

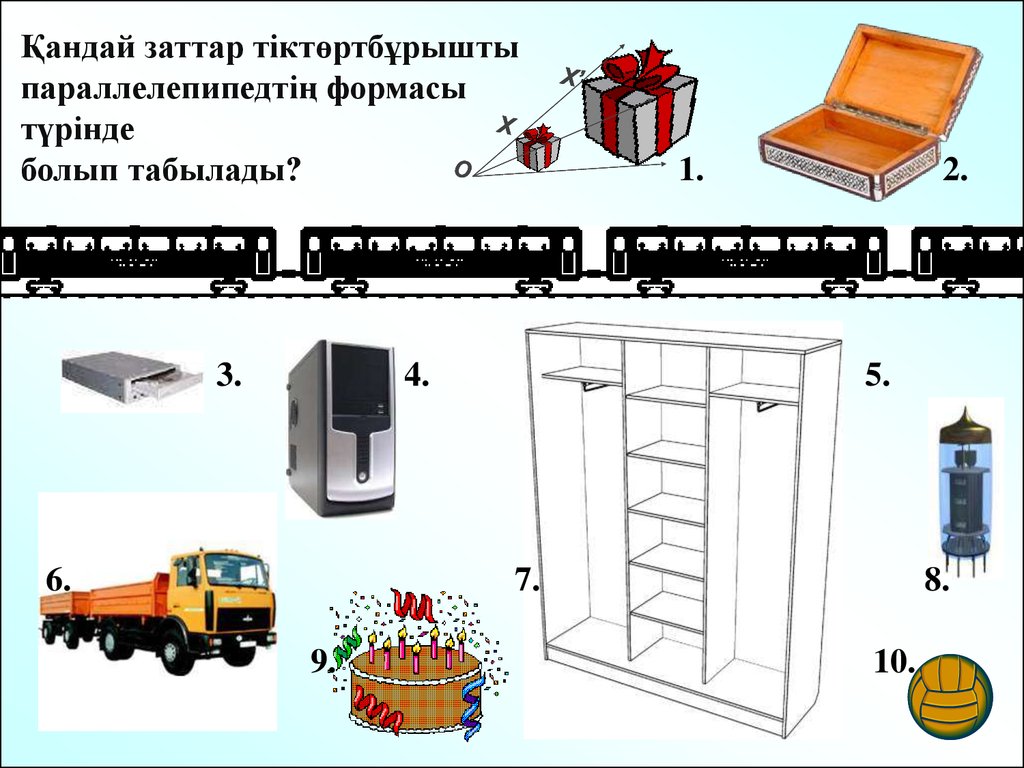
Қандай заттар тіктөртбұрышты
параллелепипедтің формасы
Х
түрінде
О
болып табылады?
3.
4.
6.
Х’
1.
2.
5.
7.
9.
8.
10.

24.

25.

1
4
3
2

26.

Куб-тікбұрышты
параллелепипед,
барлық
өлшемдері тең
Қандай геометриялық
фигуралар кубтың
жақтары болып
табылады?

27.

3
1
2

28.

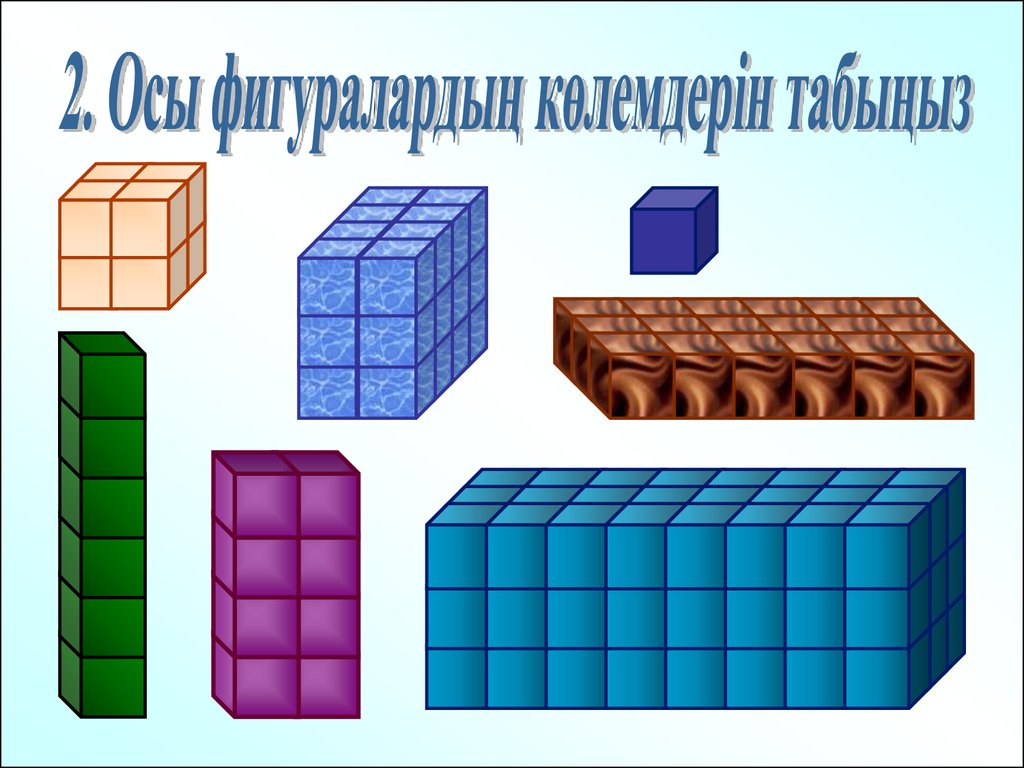
Мысалдар: 1. Параллелепипедті 1 см
қабырғасымен бірдей кубиктерден қосты.
Ол үшін неше кубик қажет болды?
С1
D1
А1
В1
5
D
4
А
8
С
В
V=8*4*5=160(см3)

29.

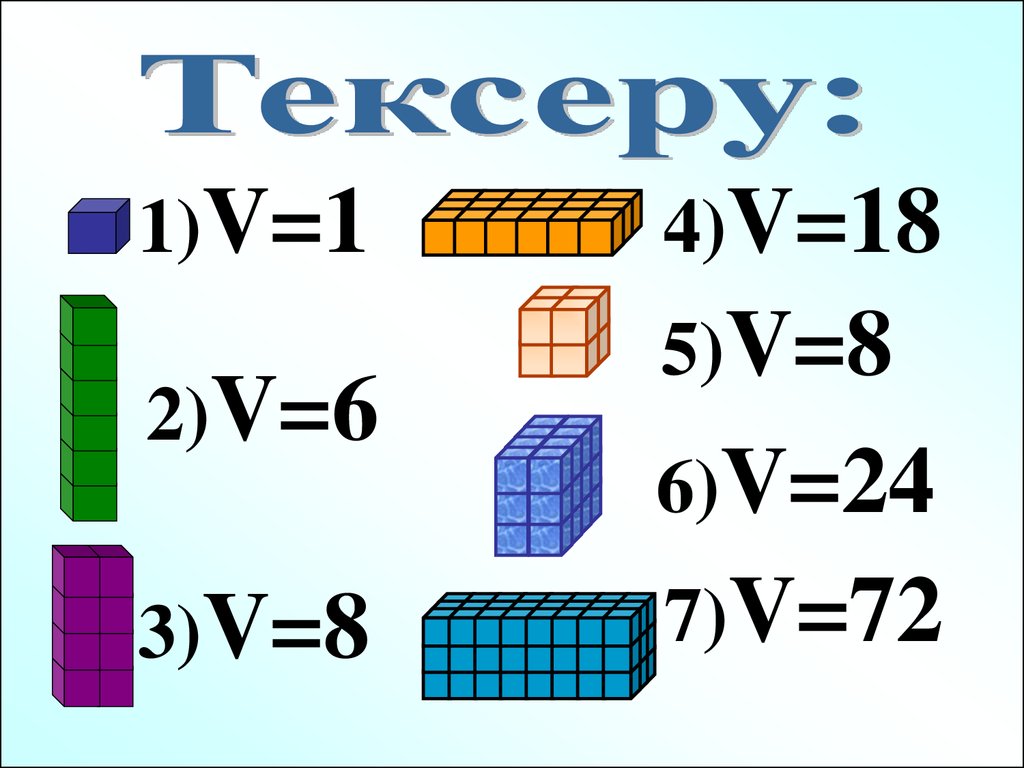
30.

1)V=1
2)V=6
3)V=8
4)V=18
5)V=8
6)V=24
7)V=72

31.

3. Дененің көлемін анықтаңыз,
егер АА1=АВ=АF=20см,
ВС=12 см, СD=8см.
С1
В1
12
В
С
8
D1
1) 203=8000(см3)
E1
V1
2) 8*8*20=1280(см3) V2
8
D
20
20
А
E
А1
3) 8000 – 1280 = 6720(см3) Vт
F1
20
F

32.

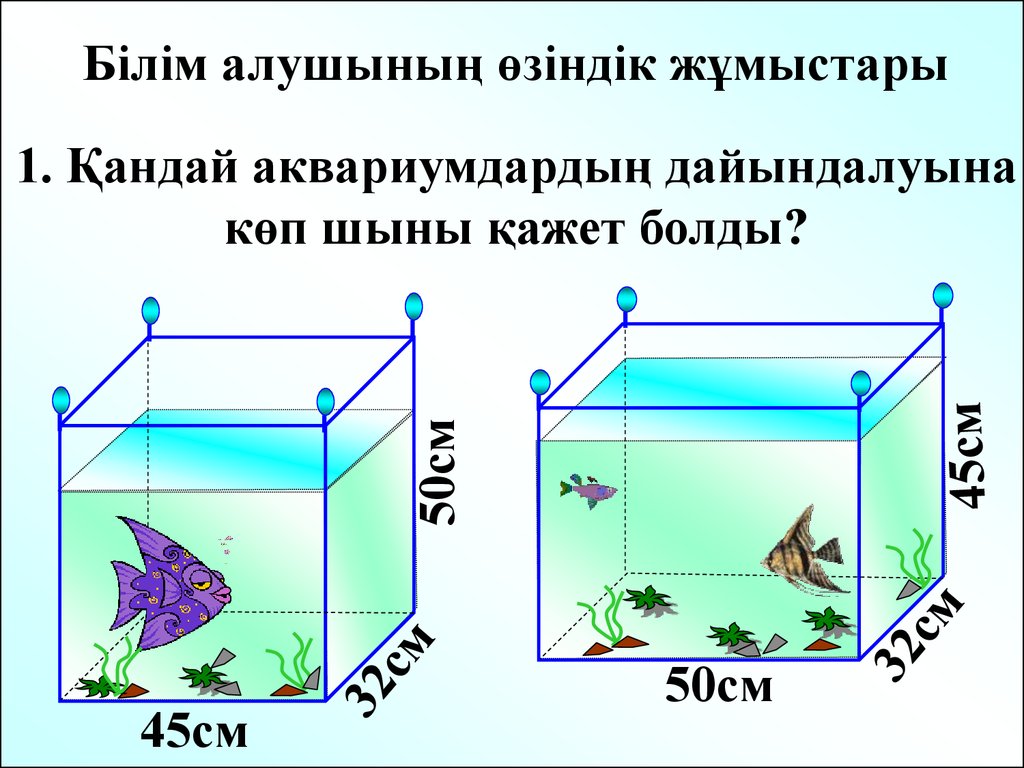
Білім алушының өзіндік жұмыстары
50см
1. Қандай аквариумдардың дайындалуына
көп шыны қажет болды?
45см
50см

33.

4,8м
7,5м

34.

3. Фигураның көлемін анықтау үшін
формуланы құрастырыңыз.
b
a-y
x
x-c
1) abx
y
V1
2) (a-y)(x-c)b V2
c
b 3) abc – (a-y)(x-c)b V
ф
a

35.

4. Фигураның көлемін есептеу үшін
формуласын құрастырыңыз.
1) a3
V1
2) aхх=ах2 V2
x
3) а3–
a
x
a
a
ах2
Vф

36.

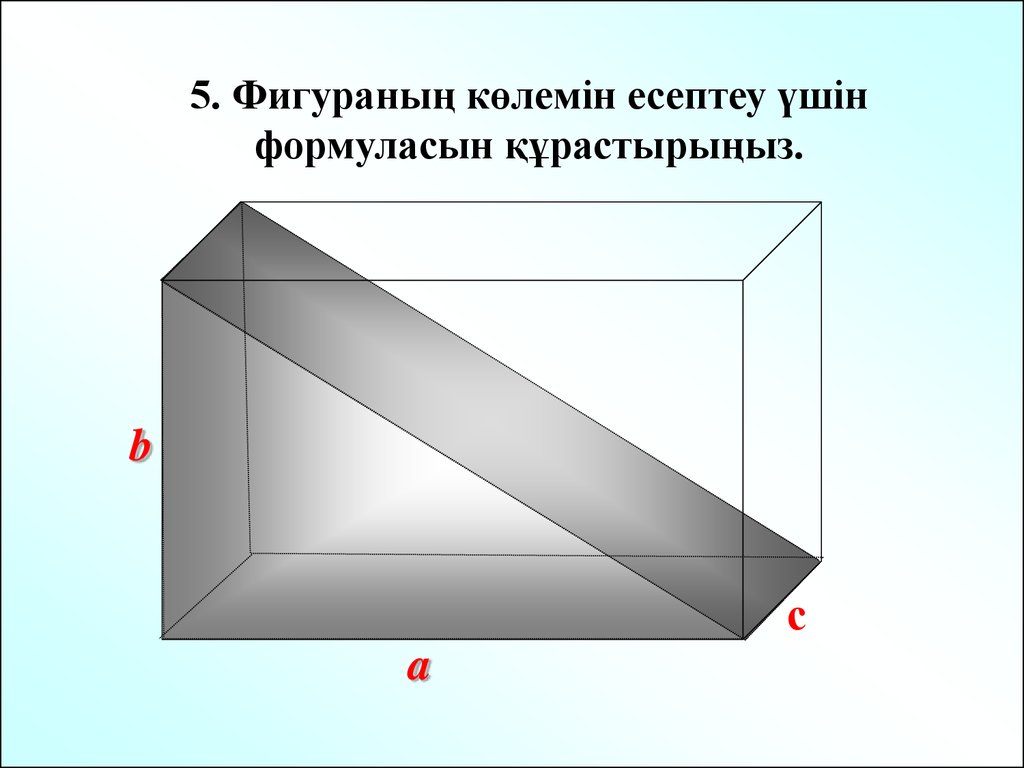
5. Фигураның көлемін есептеу үшін
формуласын құрастырыңыз.
b
с
a

37. Үй жұмысы:

Фигуралардың
моделін жасап әкелу

38. Бағалауға қойылатын талаптар:

1. Шешуі қажетті түсіндірмелер мен негіздеулерден
тұратын математикалық тілде сауатты жазылуы
керек;
2. Шешімі толық, барлық мүмкін жағдайлар
қарастырылып, ескерілуі тиіс;
3. Шешу әдісі, шешімі, жазу формасы әртүрлі болуы
мүмкін, бірақ шешімі толық негізделген.

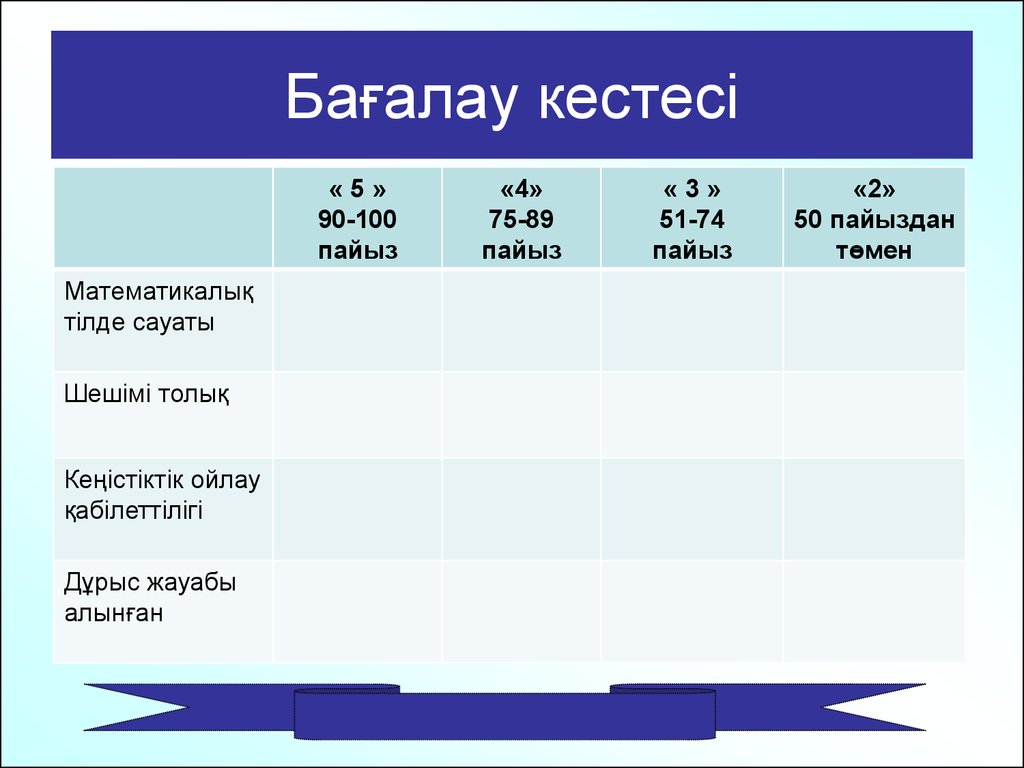
39. Бағалау кестесі

«5»
90-100
пайыз
Математикалық
тілде сауаты
Шешімі толық
Кеңістіктік ойлау
қабілеттілігі
Дұрыс жауабы
алынған
«4»
75-89
пайыз
«3»
51-74
пайыз
«2»
50 пайыздан
төмен

40.

Рубинштейн С.Л. Проблема способности и вопросы психологических теорий. М.: Педагогика, 1973 г.
•Якиманская И.С. Развитие пространственного мышления школьников. М.: Педагогика, 1988.
•Колмогоров А.Н. О системе основных понятий и обозначении для школьного курса математики. (МВШ, 1971, № 2).
•Столяр А.А. Педагогика математики. – Минск: Высшая школа, 1986
•Абылқасымова А.Е. Методика преподавания математики. Алматы, - Санат, 1993 г.
•Оразалиев А. «Математикалық сөйлемдер». Алматы, 1996 г.

41.

42. Anymeeting программасымен жұмыс жасау

43. Табиғаттағы ұғымның логикалық талдауы

44. Қолданылған әдебиеттер

1. Пиаже Ж. Психология интеллекта. Избранные психологические
труды. – Пер. с англ. и франц. – М.: Международная
педагогическая академия., 1994 г.
2. Рубинштейн С.Л. Проблема способности и вопросы
психологических теорий. М.: Педагогика, 1973 г.
3. Якиманская И.С. Развитие пространственного мышления
школьников. М.: Педагогика, 1988.
4. Колмогоров А.Н. О системе основных понятий и обозначении
для школьного курса математики. (МВШ, 1971, № 2).
5. Столяр А.А. Педагогика математики. – Минск: Высшая школа,
1986
6. Абылқасымова А.Е. Методика преподавания математики.
Алматы, - Санат, 1993 г.
7. Оразалиев А. «Математикалық сөйлемдер». Алматы, 1996 г.

45. Назар қойып тыңдағандарыңызға рахмет!

МАТЕМАТИКА ғылымдар патшасы!