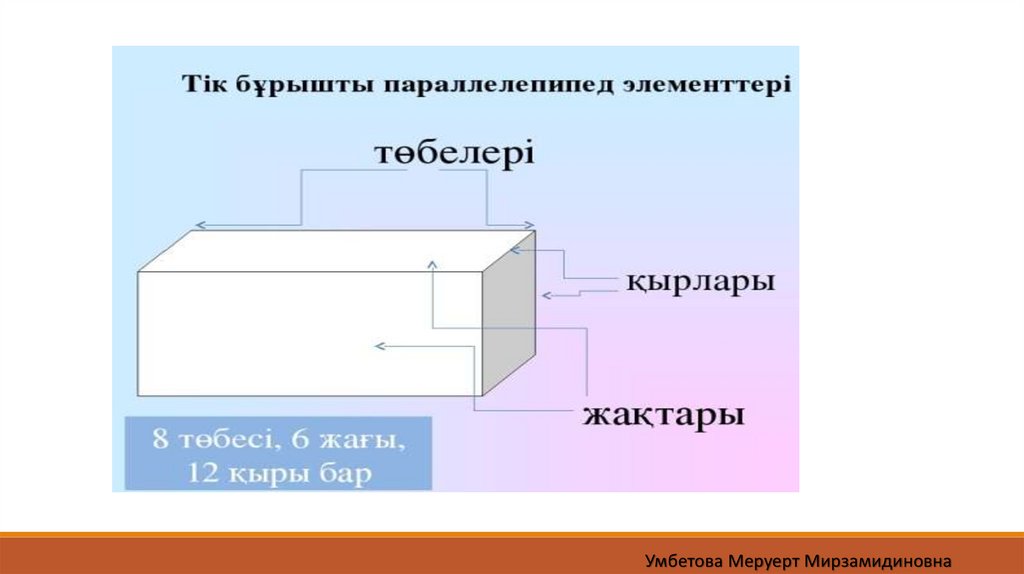
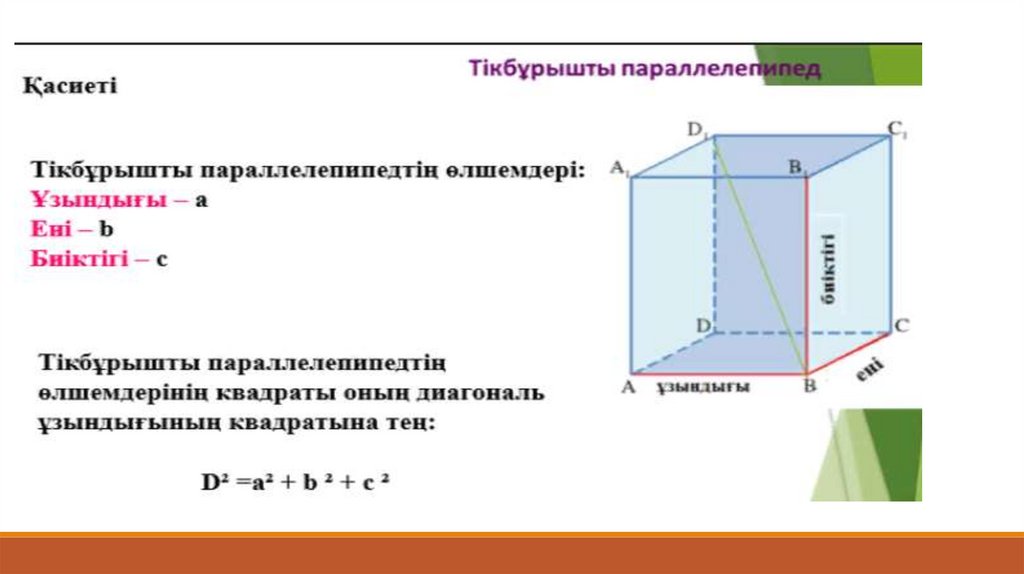
Тікбұрышты параллелепипед

1.

10 сынып. Геометрия. ЖМБ
Сабақтың тақырыбы:Тікбұрышты
параллелепипед
10.1.2 - тікбұрышты параллелепипед анықтамасын
және қасиеттерін білу;
10.3.7 - тікбұрышты параллелепипедтің қасиеттерін
қорытып шығару және есептер шығаруда қолдану;
Умбетова Меруерт Мирзамидиновна

2.

Умбетова Меруерт Мирзамидиновна

3.

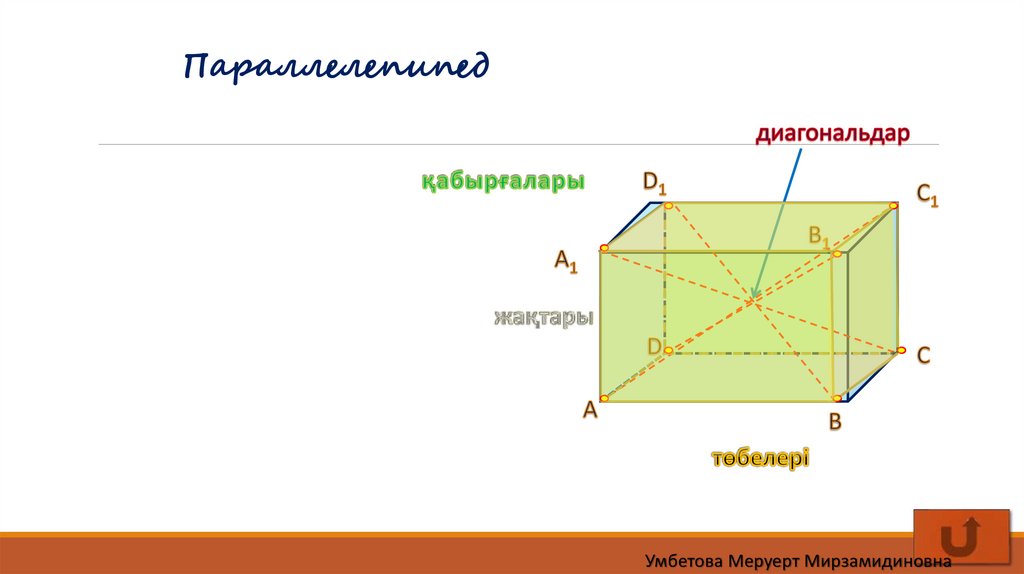
Параллелепипед
Умбетова Меруерт Мирзамидиновна

4.

Умбетова Меруерт Мирзамидиновна

5.

Умбетова Меруерт Мирзамидиновна

6.

7.

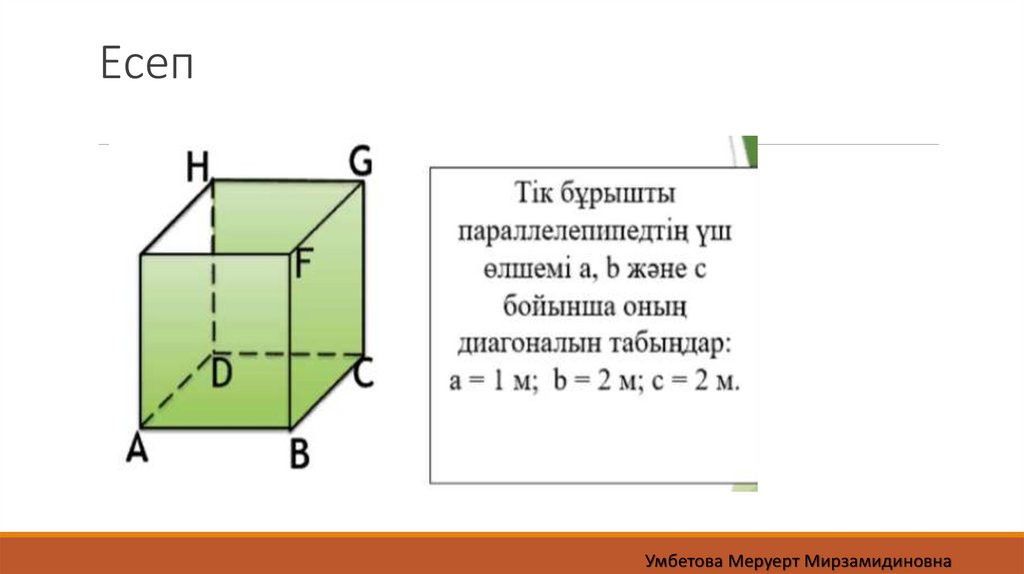
Есептер
Есеп шығару А-деңгей.
№1.Тік бұрышты параллелепипедтің үш өлшемі берілген. а=1 м, b=2 м,
с=2 м
1)диагоналін табыңыз (1 балл)
2)толық бетінің ауданын табыңыз (1 балл)
3)диагональдық қимасының ауданын табыңыз (2 балл)
Жауабы:1)3 м; 2)16 см2; 3)2 см немесе 2
№2. Тік параллелепипедтің табанының қабырғалары а=5 м, b=8 м,олардың
арасындағы бұрышы 300, биіктігі с=10 м.
1)бүйір бетінің ауданын табыңыз (1 балл)
2)толық бетінің ауданын табыңыз (2 балл)Жауабы:1)260 см2; 2) 300 см2.
Умбетова Меруерт Мирзамидиновна

8.

есептер
В-деңгей.
№1.Бір төбесіндегі үш жағының аудандары бойынша 21 м2, 33 м2, 77 м2
тік бұрышты параллелепипедтің үш өлшемін табыңыз. (5
балл)Жауабы:3 м, 7 м, 11 м.
№2. Тік бұрышты параллелепипедтің бүйір қыры 5 см, табан ауданы 360
см2, ал табанының диагоналі
41 см. Параллелепипедтің бүйір бетінің ауданын табыңыз. (5
балл)Жауабы: 490 см2.
Умбетова Меруерт Мирзамидиновна

9.

есептер
с-деңгей.
№1. Тік бұрышты параллелепипедтің табанының қабырғаларының
қатынасы 3:4 қатынасындай, ал диагональдық қимасының ауданы
15 см2. Параллелепипедтің бүйір бетінің ауданын табыңыз.
(8 балл)Жауабы: 42 см2.
№2. Тік параллелепипедтің табан қабырғалары 13 см және 14 смге, кіші диагоналы 17 см-ге, ал табанының ауданы 168 см2-қа тең.
Параллелепипедтің бүйір бетінің ауданын табыңыз. (10 балл)
Умбетова Меруерт Мирзамидиновна

10.

Есеп
Умбетова Меруерт Мирзамидиновна

11.

12.

Умбетова Меруерт Мирзамидиновна

13.

жауаптары
Умбетова Меруерт Мирзамидиновна

14.

15.

Жазық фигураның
жазықтыққа ортогональ
проекциясы және оның
ауданы

16.

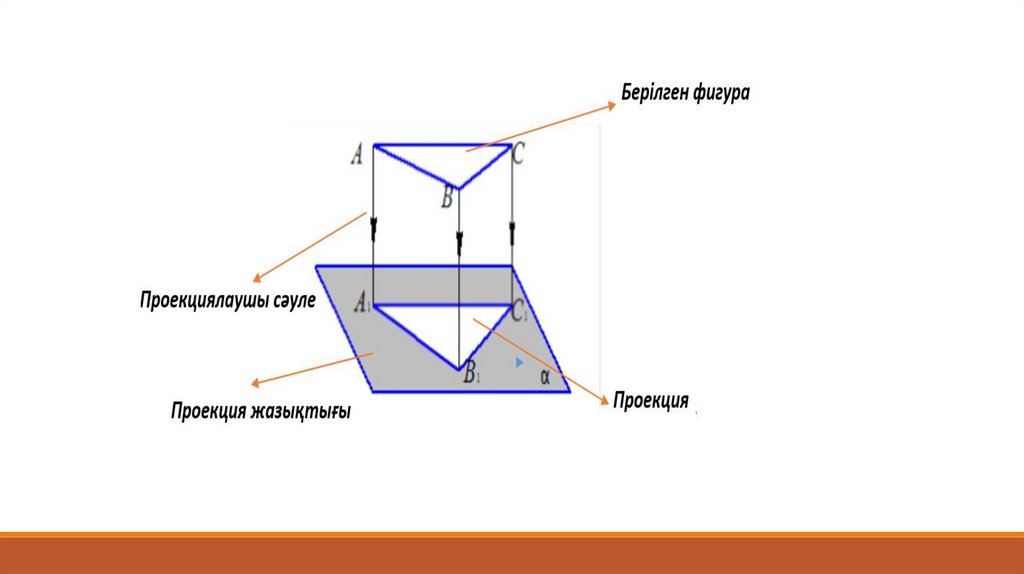
Жаңа материалмен танысу
Жаңа материалмен танысу: Проекциялау деп жазықтықта (қағазда,
экранда, дәптерде) нәрсенің кескінін салу процесін айтады. Бұл жағдайда
алынған кескінді проекция дейміз «Проекция» дегеніміз латын сөзі,
«алдыға лақтыру» деген мағынаны білдіреді Электр шамының алдында
қандай да бір затты орналастырайық сонда оның қабырғада пайда болған
көлеңкесін нәрсенің проекциясы деп айтуға болады.
Кеңістіктік фигураларды жазықтыққа кескіндеу үшін параллель
проекциялауды пайдаланады.
Фигураны кескіндеудің осы тәсілі: Кеңістікте F фигурасы мен α жазықтығы
берілсін, α жазықтығын қиятын l түзуін аламыз. F фигурасының әрбір
нүктесінен l түзуіне параллель түзулер жүргіземіз. Бұл түзулер π
жазықтығымен қиылысқанда, F' жазық фигурасы шығады.
Жазық F фигурасы l түзуіне параллель проекциялаудан алынған F
фигурасының π жазықтығындағы проекциясы деп аталады. Мұндағы l түзуі
– проекциялаушы түзу, π – проекция жазықтығы.

17.

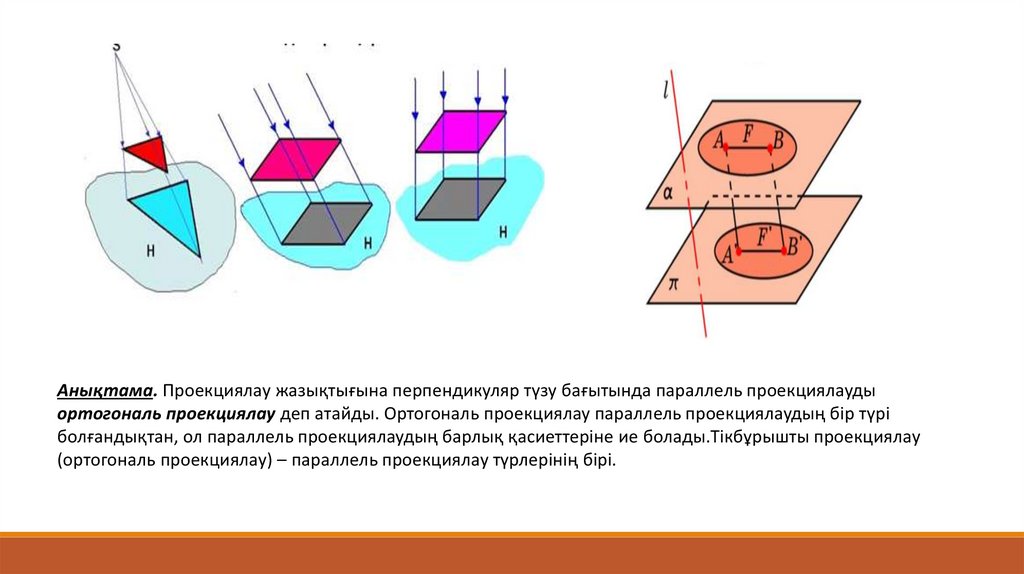
Анықтама. Проекциялау жазықтығына перпендикуляр түзу бағытында параллель проекциялауды
ортогональ проекциялау деп атайды. Ортогональ проекциялау параллель проекциялаудың бір түрі
болғандықтан, ол параллель проекциялаудың барлық қасиеттеріне ие болады.Тікбұрышты проекциялау
(ортогональ проекциялау) – параллель проекциялау түрлерінің бірі.

18.

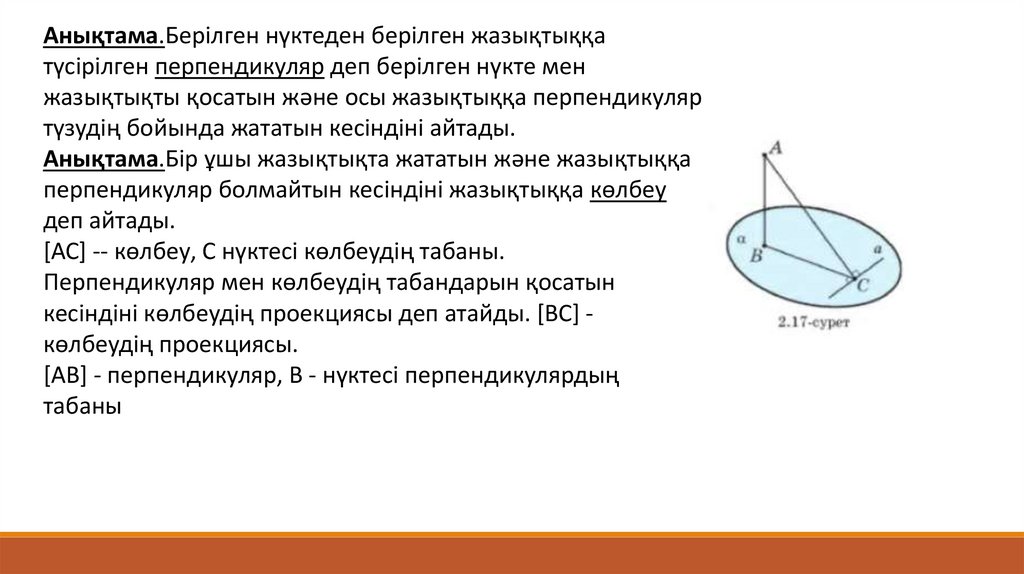
Анықтама.Берілген нүктеден берілген жазықтыққа
түсірілген перпендикуляр деп берілген нүкте мен
жазықтықты қосатын және осы жазықтыққа перпендикуляр
түзудің бойында жататын кесіндіні айтады.
Анықтама.Бір ұшы жазықтықта жататын және жазықтыққа
перпендикуляр болмайтын кесіндіні жазықтыққа көлбеу
деп айтады.
[АС] -- көлбеу, С нүктесі көлбеудің табаны.
Перпендикуляр мен көлбеудің табандарын қосатын
кесіндіні көлбеудің проекциясы деп атайды. [ВС] көлбеудің проекциясы.
[АВ] - перпендикуляр, В - нүктесі перпендикулярдың
табаны

19.

20.

21.

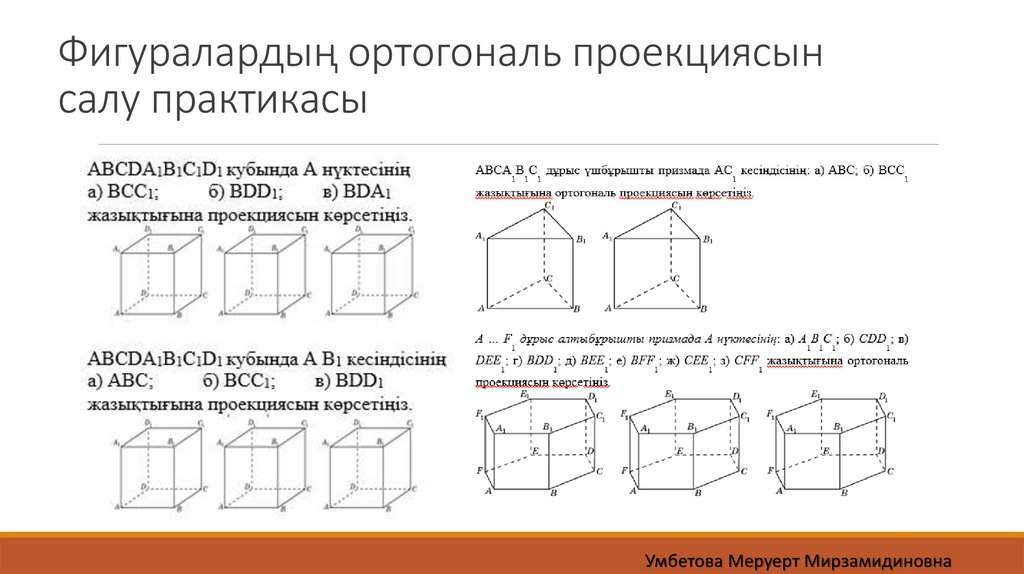
Фигуралардың ортогональ проекциясын
салу практикасы
Умбетова Меруерт Мирзамидиновна

22.

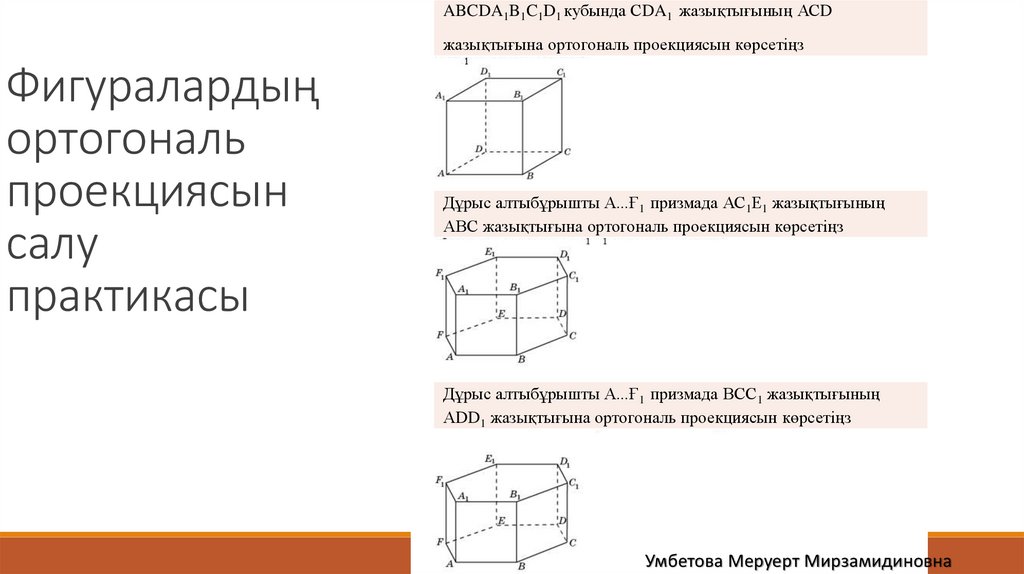
ABCDA1B1C1D1 кубында СDA1 жазықтығының АСD
жазықтығына ортогональ проекциясын көрсетіңз
Фигуралардың
ортогональ
проекциясын
салу
практикасы
Дұрыс алтыбұрышты A...Ғ1 призмада АС1Е1 жазықтығының
АВС жазықтығына ортогональ проекциясын көрсетіңз
Дұрыс алтыбұрышты A...Ғ1 призмада ВСС1 жазықтығының
АDD1 жазықтығына ортогональ проекциясын көрсетіңз
Умбетова Меруерт Мирзамидиновна

23.

24.

25.

26.

27.

28.

29.

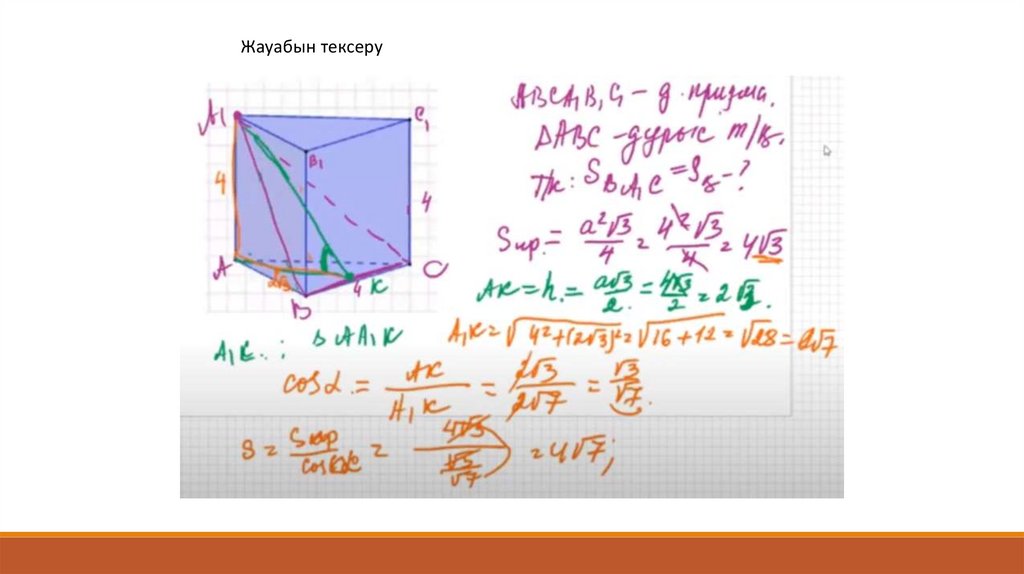
Жауабын тексеру

30.

31.

Жауабын тексеру

32.

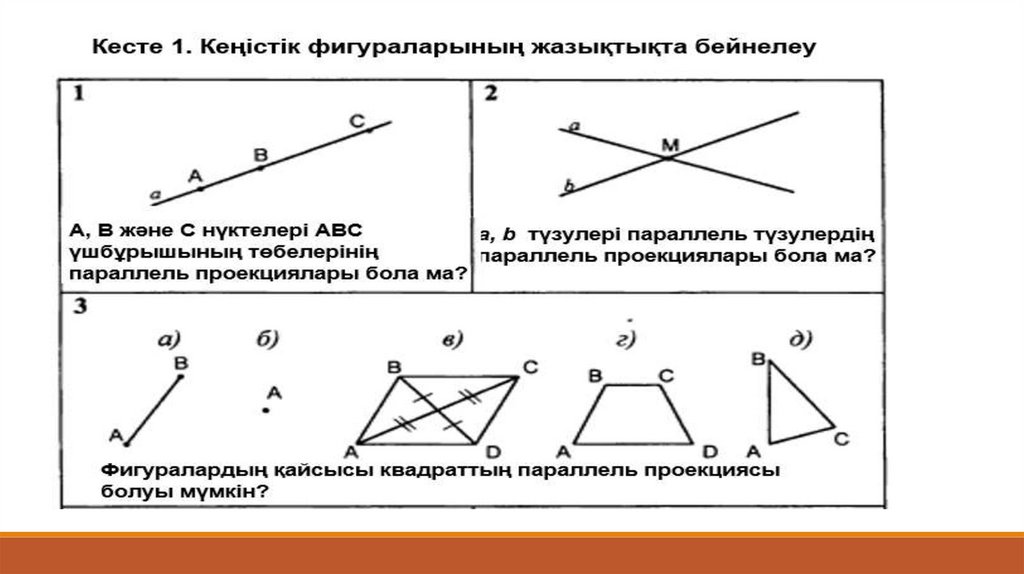
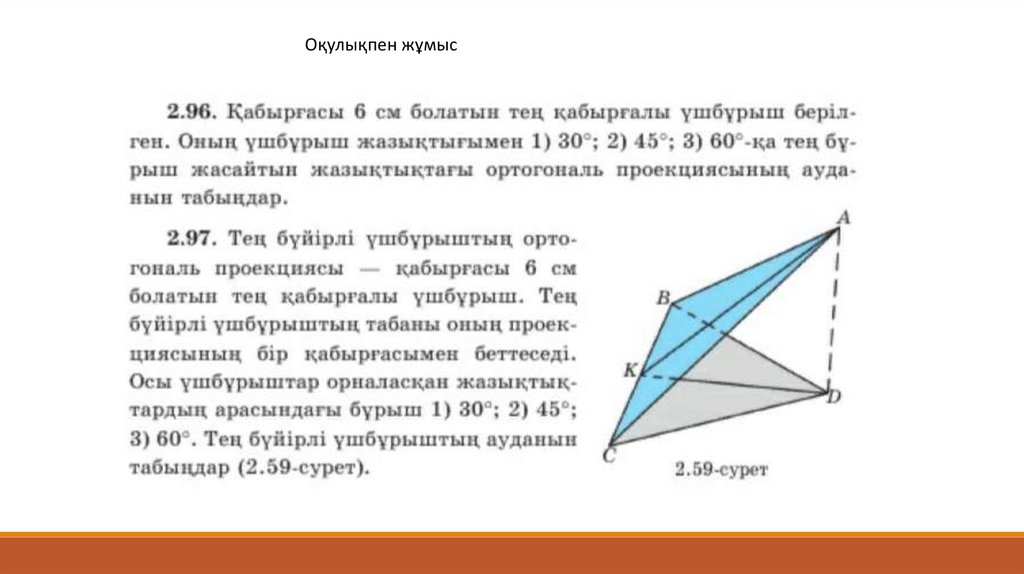
Оқулықпен жұмыс
№2.93. Кесіндінің проекциясы осы кесіндінің өзінен узын болуы
мумкін бе? Жауаптарынды сызба аркылы негіздендер.
№2.94. Параллель емес тузулердіц проекциялары параллель
болуы мумкін бе? Мысал келтіріңдер.
№2.95. Көпбурыш жазыктығы проекциялау багытына параллель
емес. 1) Ушбурыш; 2) квадрат; 3) тіктөртбурыш; 4)
параллелограмм; 5) трапеция кандай фигурага
проекцияланады?

33.

Оқулықпен жұмыс

34.

10.4.1 - кеңістіктегі вектор, вектордың ұзындығы, тең векторлар анықтамаларын білу,
10.4.2 - векторларды қосу және векторды санға көбейтуді орындау;
10.4.3 - кеңістіктегі коллинеар және компланар векторлардың анықтамаларын білу;

35.

36.

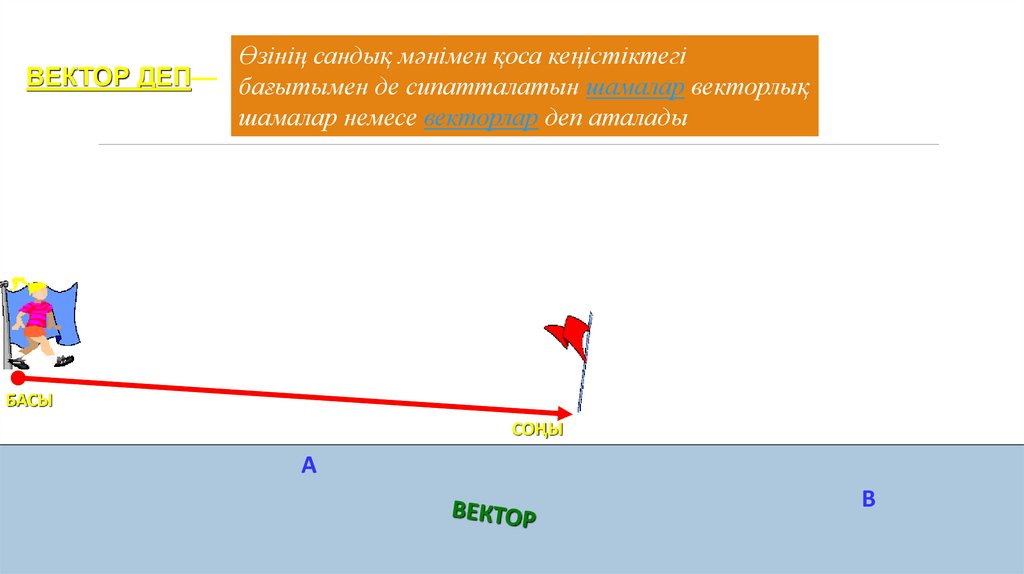
Өзінің сандық мәнімен қоса кеңістіктегі
ВЕКТОР ДЕП— бағытымен де сипатталатын шамалар векторлық
шамалар немесе векторлар деп аталады
БАСЫ
СОҢЫ
А
В

37.

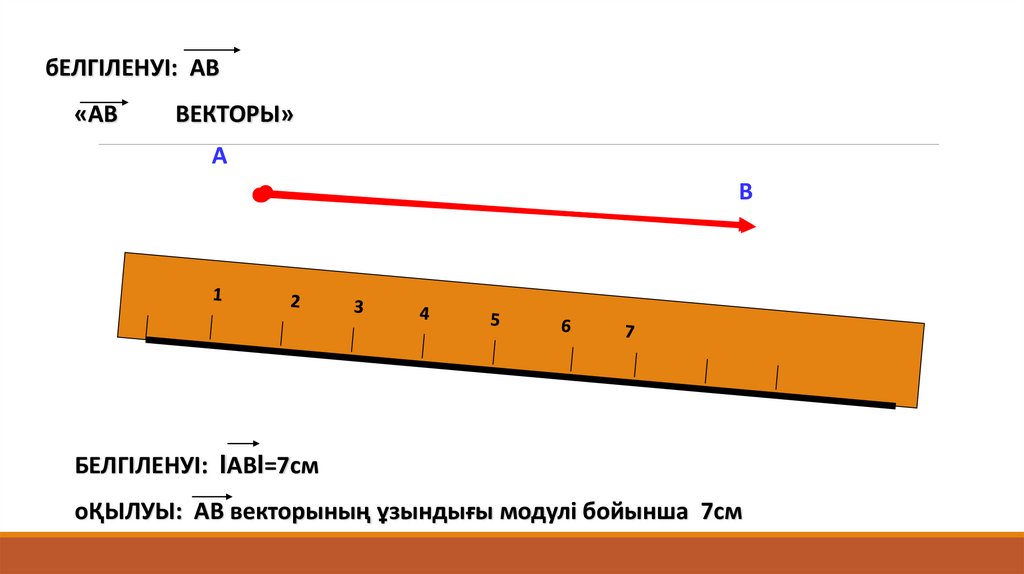
бЕЛГІЛЕНУІ: АВ
«АВ
ВЕКТОРЫ»
А
В
БЕЛГІЛЕНУІ: IАВI=7cм
оҚЫЛУЫ: АВ векторының ұзындығы модулі бойынша 7см

38.

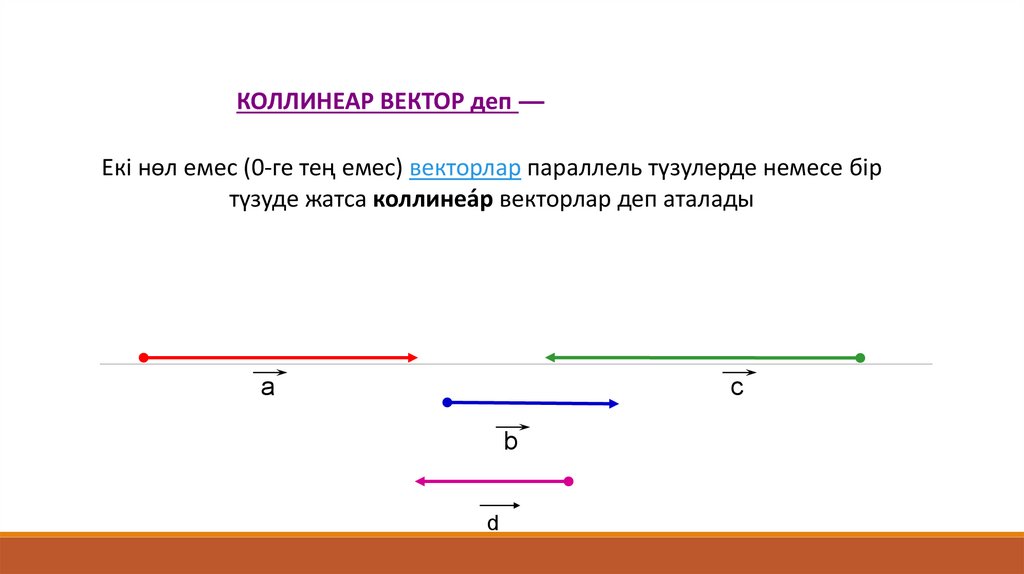
КОЛЛИНЕАР ВЕКТОР деп —
Екі нөл емес (0-ге тең емес) векторлар параллель түзулерде немесе бір
түзуде жатса коллинеа́р векторлар деп аталады
а
с
b
d

39.

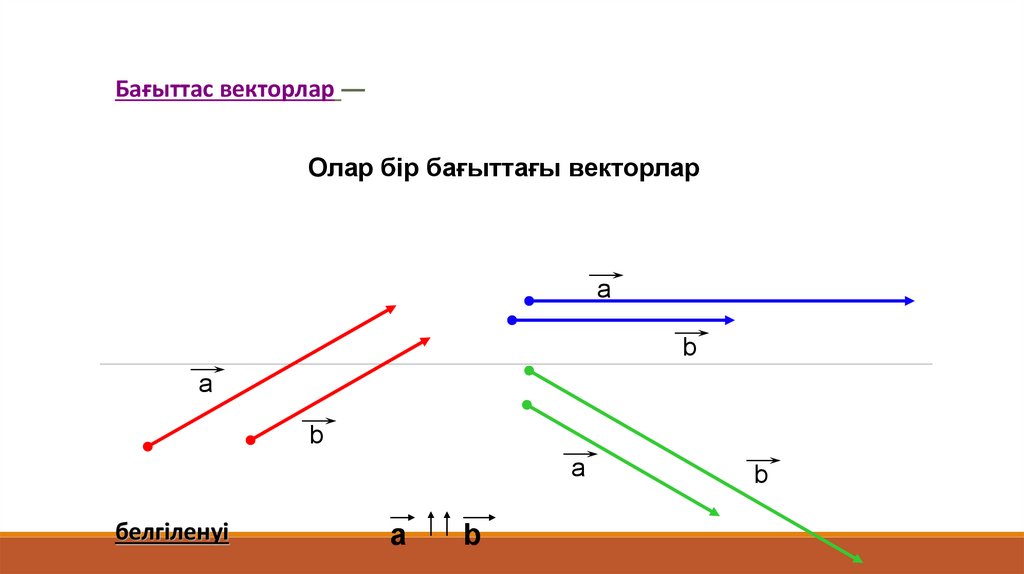
Бағыттас векторлар —
Олар бір бағыттағы векторлар
а
b
а
b
а
белгіленуі
а
b
b

40.

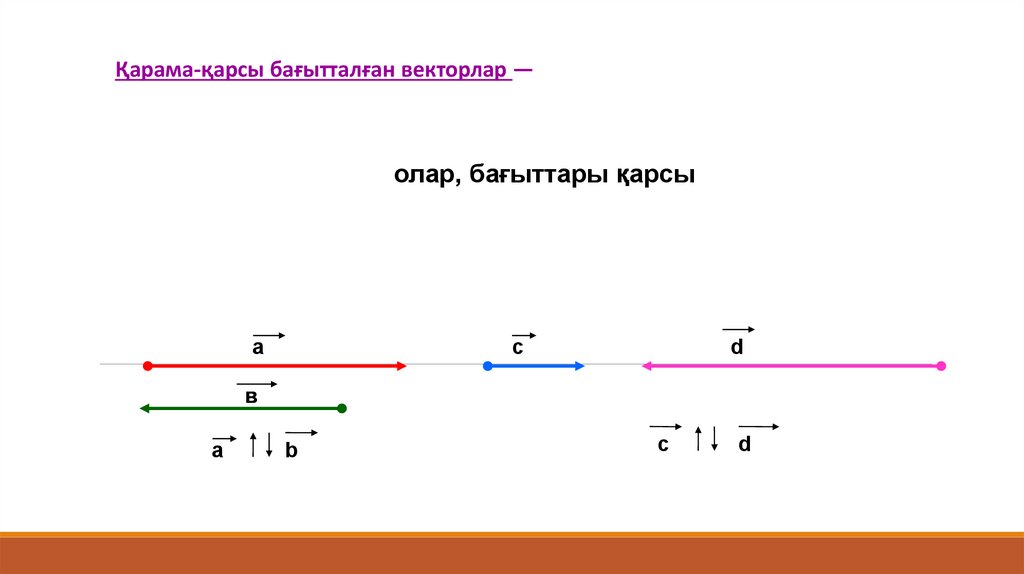
Қарама-қарсы бағытталған векторлар —
олар, бағыттары қарсы
а
с
d
в
а
b
с
d

41.

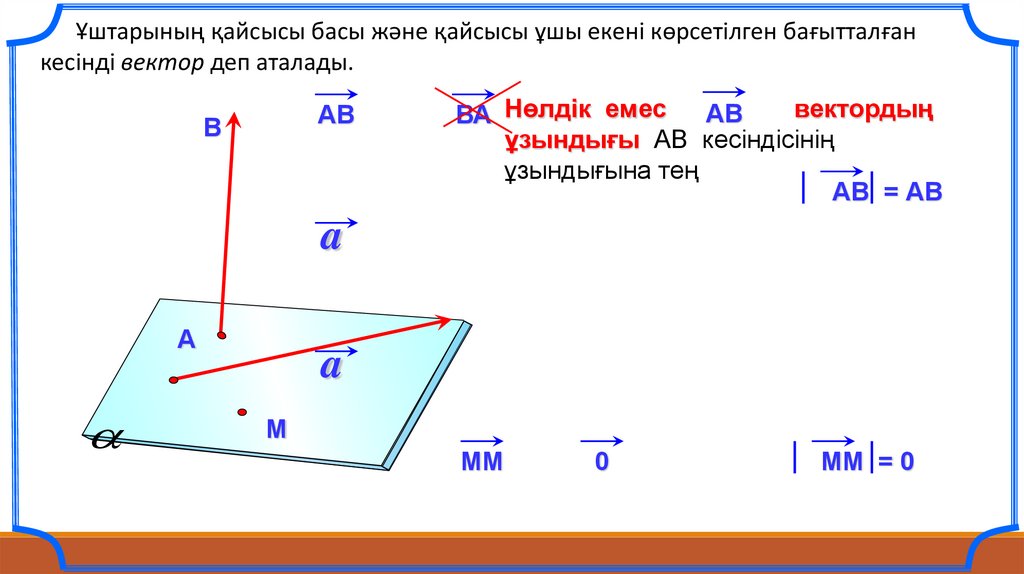
Ұштарының қайсысы басы және қайсысы ұшы екені көрсетілген бағытталған
кесінді вектор деп аталады.
АВ
В
вектордың
АВ
ВА Нөлдік емес
ұзындығы АВ кесіндісінің
ұзындығына тең
АВ = АВ
a
А
a
M
MM
0
MM = 0

42.

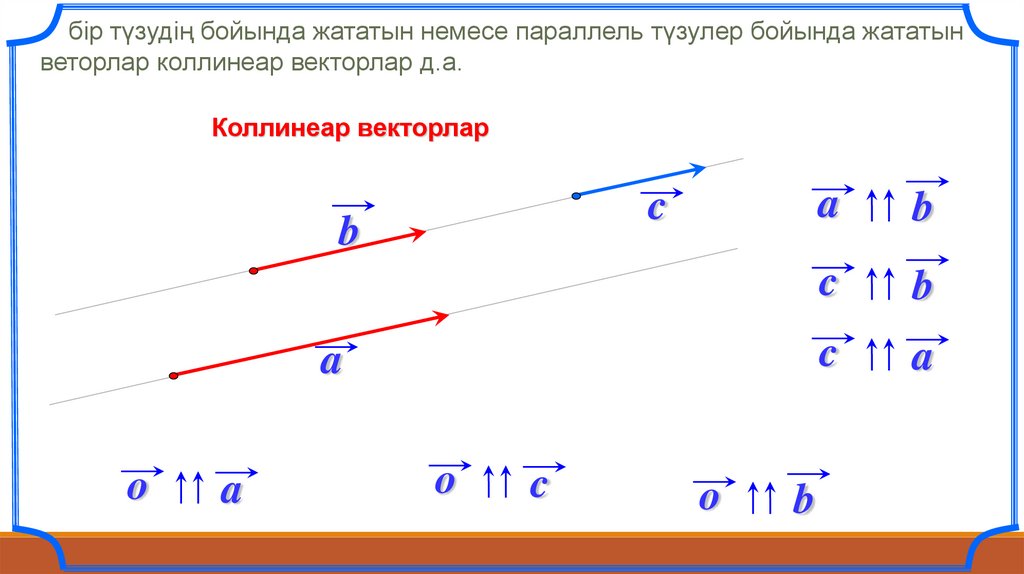
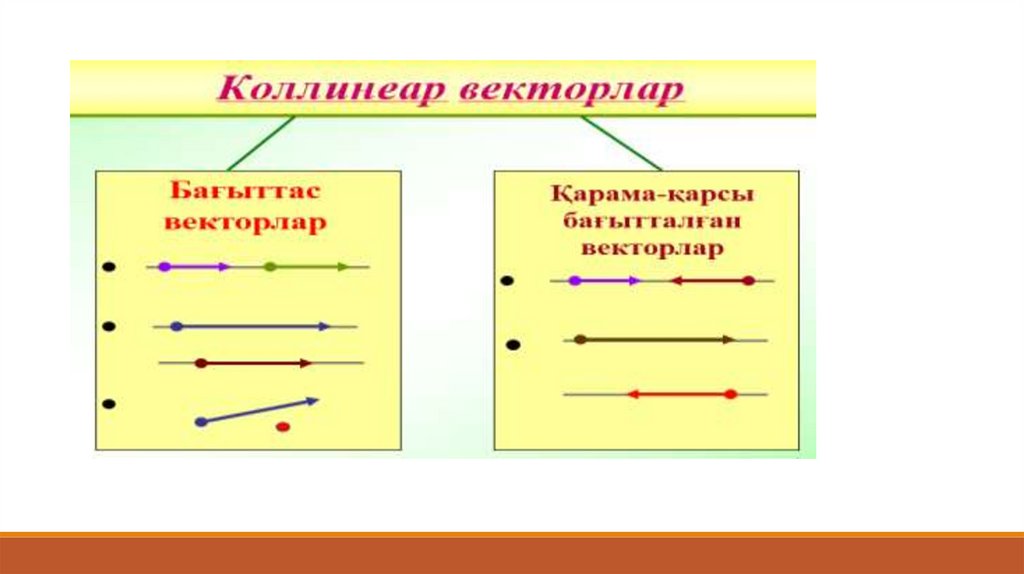
бір түзудің бойында жататын немесе параллель түзулер бойында жататын
веторлар коллинеар векторлар д.а.
Коллинеар векторлар
c
b
a
o
a
o
c
o
b
a
b
c
b
c
a

43.

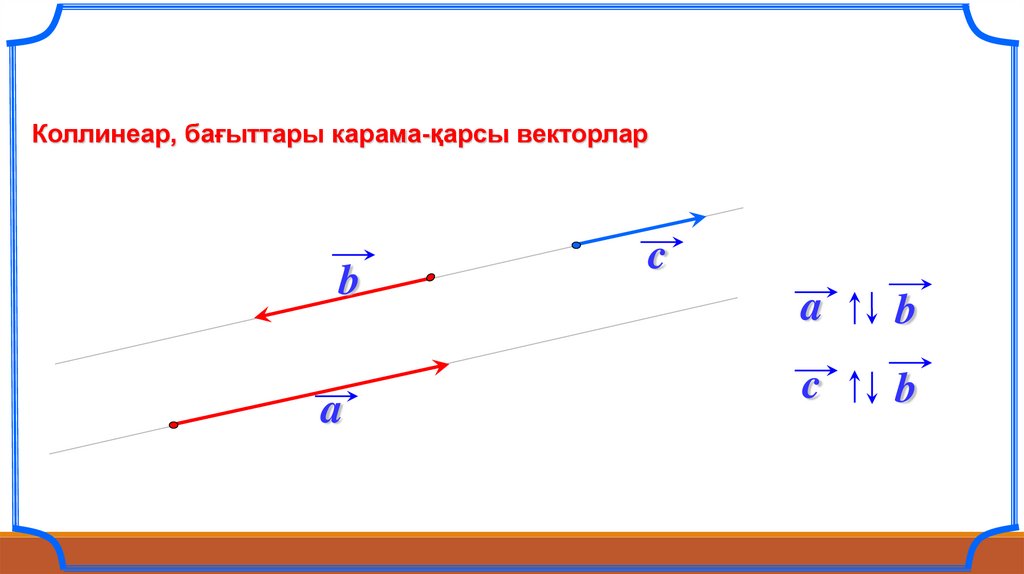
Коллинеар, бағыттары карама-қарсы векторлар
b
a
c
a
b
c
b

44.

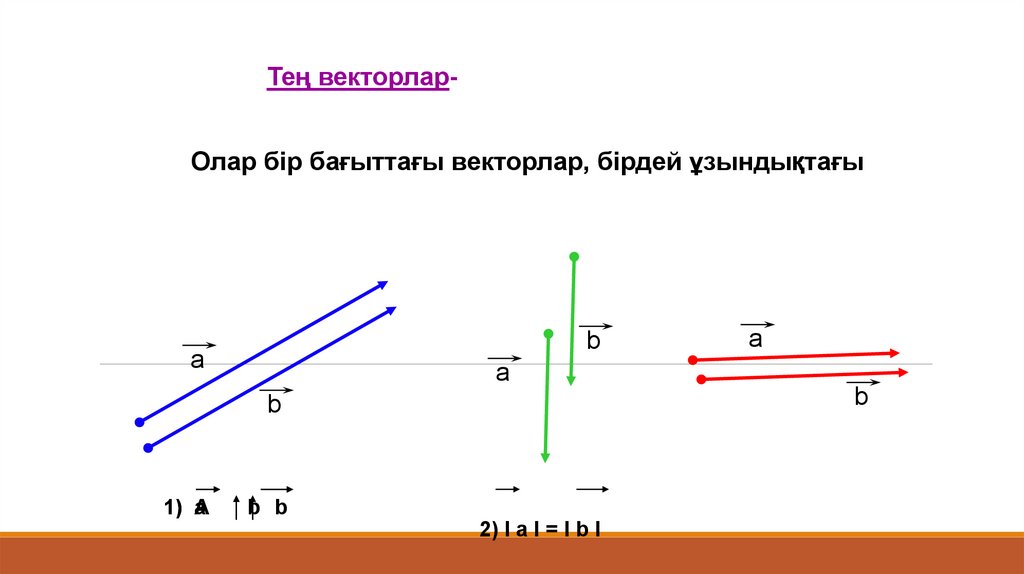
Тең векторларОлар бір бағыттағы векторлар, бірдей ұзындықтағы
b
а
а
b
b
1) А
а
а
b b
2) I а I = I b I

45.

46.

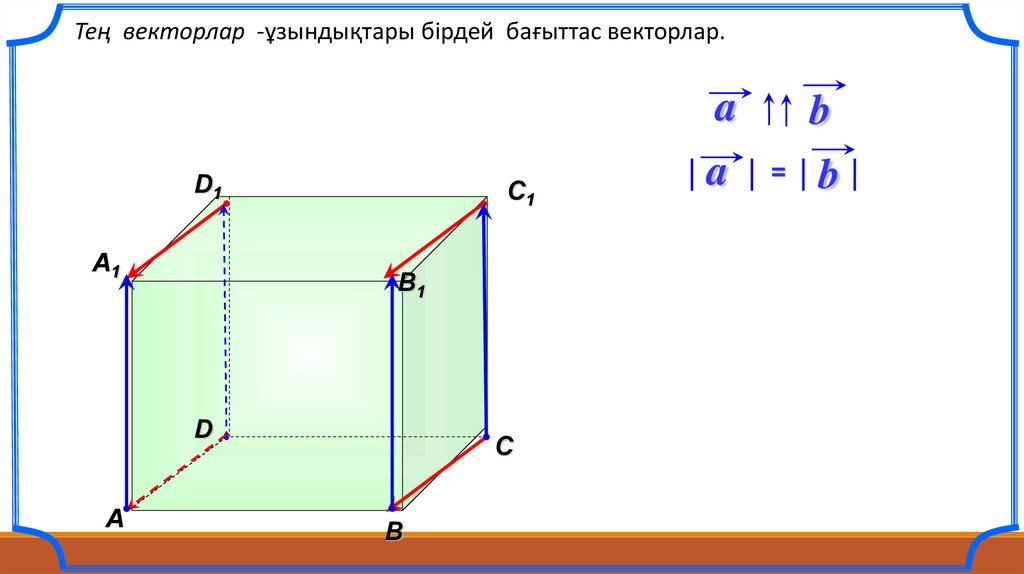
Тең векторлар -ұзындықтары бірдей бағыттас векторлар.
a
D1
A1
C1
B1
D
A
C
B
a
b
=
b

47.

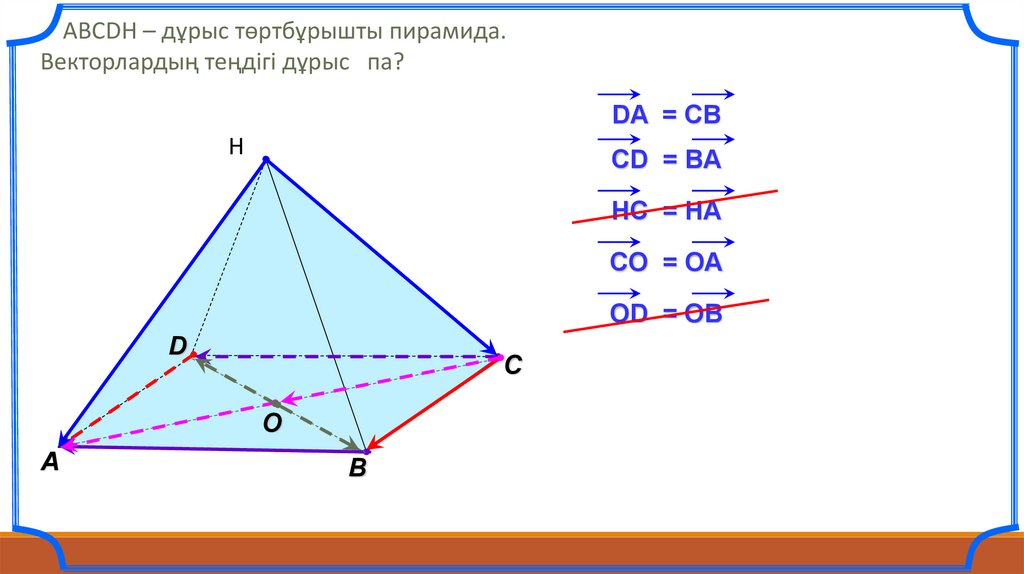
АВСDH – дұрыс төртбұрышты пирамида.
Векторлардың теңдігі дұрыс па?
DA = CB
Н
CD = BA
HC = HA
CO = OA
OD = OB
D
С
O
А
В

48.

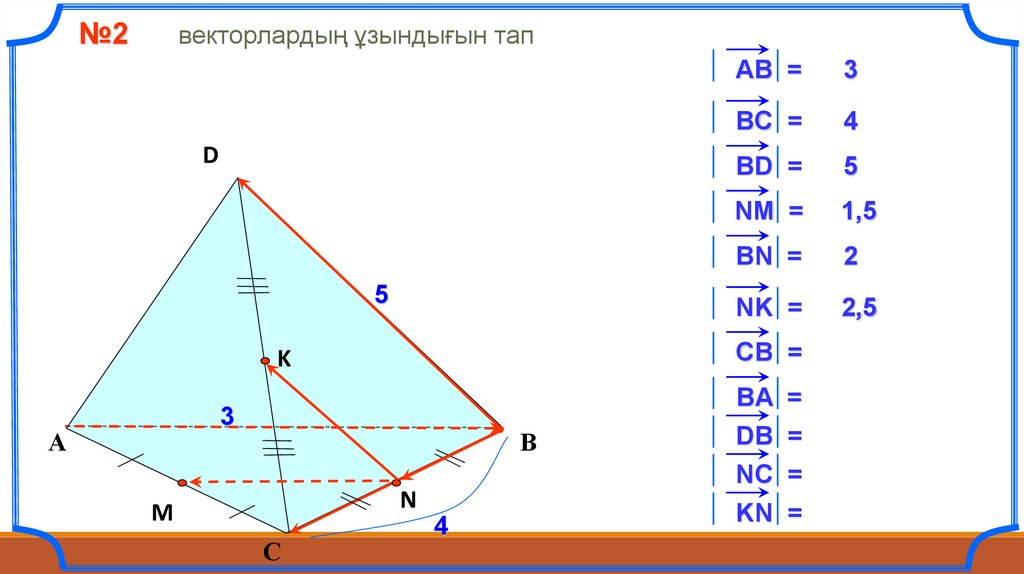
№2
векторлардың ұзындығын тап
D
S
5
3
В
N
M
С
3
ВC =
4
ВD =
5
NM =
1,5
BN =
2
NK =
2,5
CB =
K
А
АВ =
4
BA =
DB =
NC =
KN =

49.

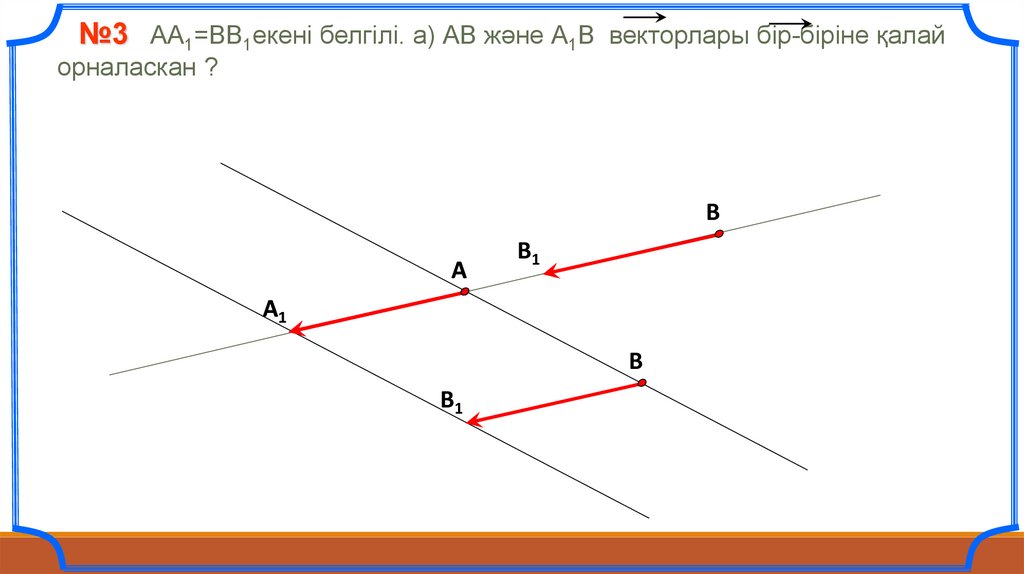
№3 АА1=ВВ1екені белгілі. а) АВ және А1В векторлары бір-біріне қалай
орналаскан ?
В
А
В1
А1
В
В1

50.

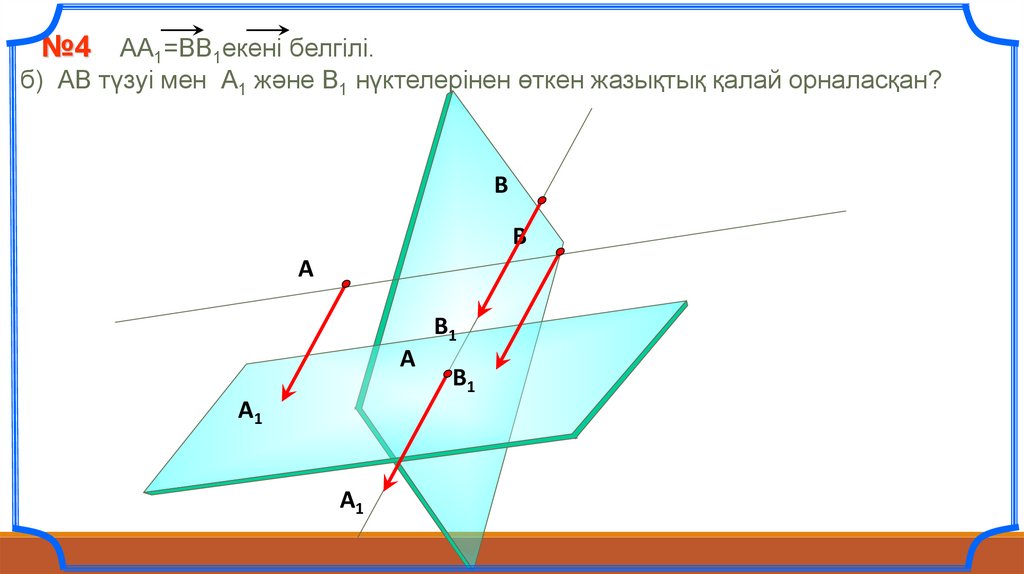
№4 АА1=ВВ1екені белгілі.
б) АВ түзуі мен А1 және В1 нүктелерінен өткен жазықтық қалай орналасқан?
В
В
А
В1
А
А1
А1
В1

51.

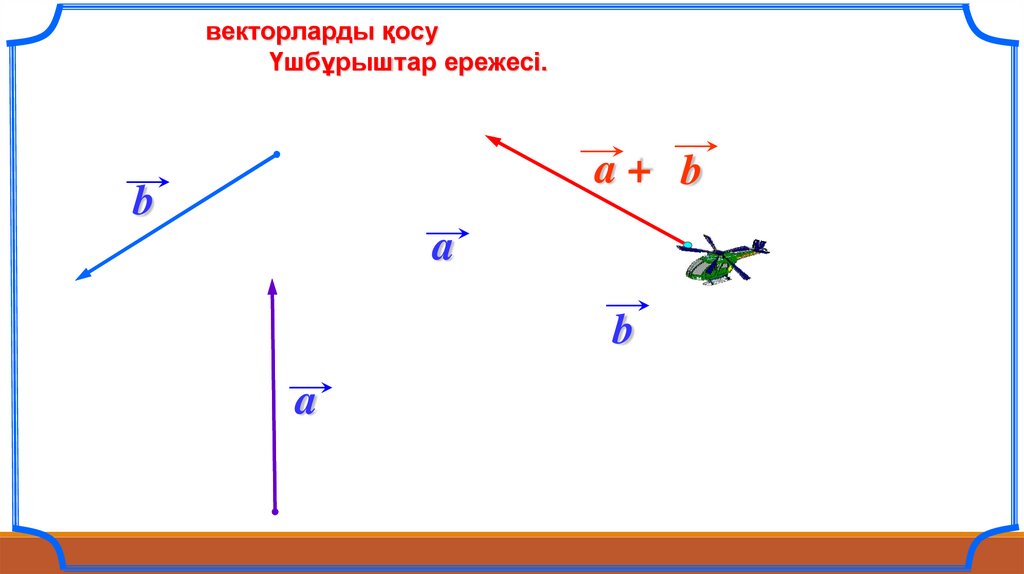
векторларды қосу
Үшбұрыштар ережесі.
a+ b
b
a
b
a

52.

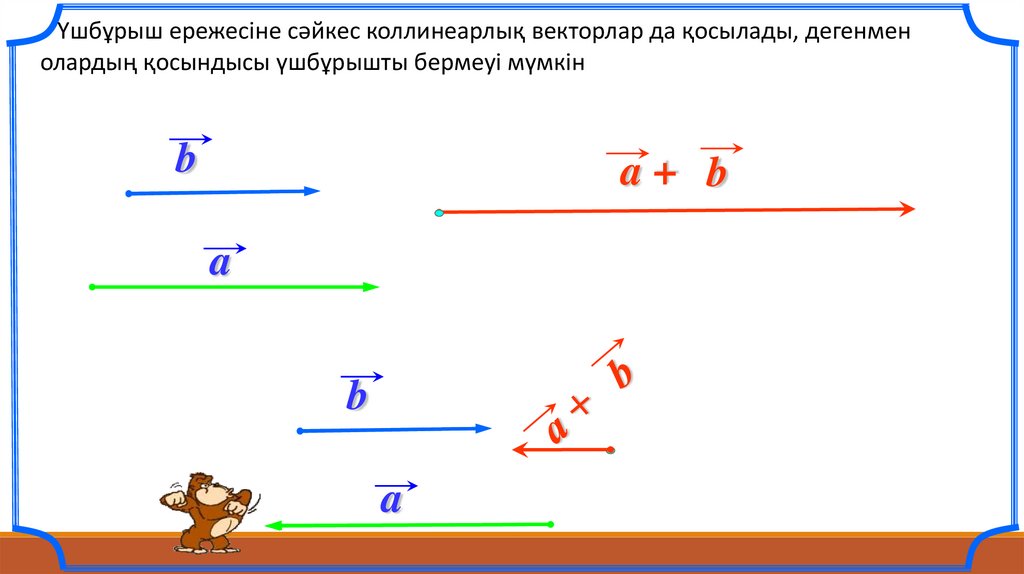
Үшбұрыш ережесіне сәйкес коллинеарлық векторлар да қосылады, дегенмен
олардың қосындысы үшбұрышты бермеуі мүмкін
b
a+ b
a
b
a

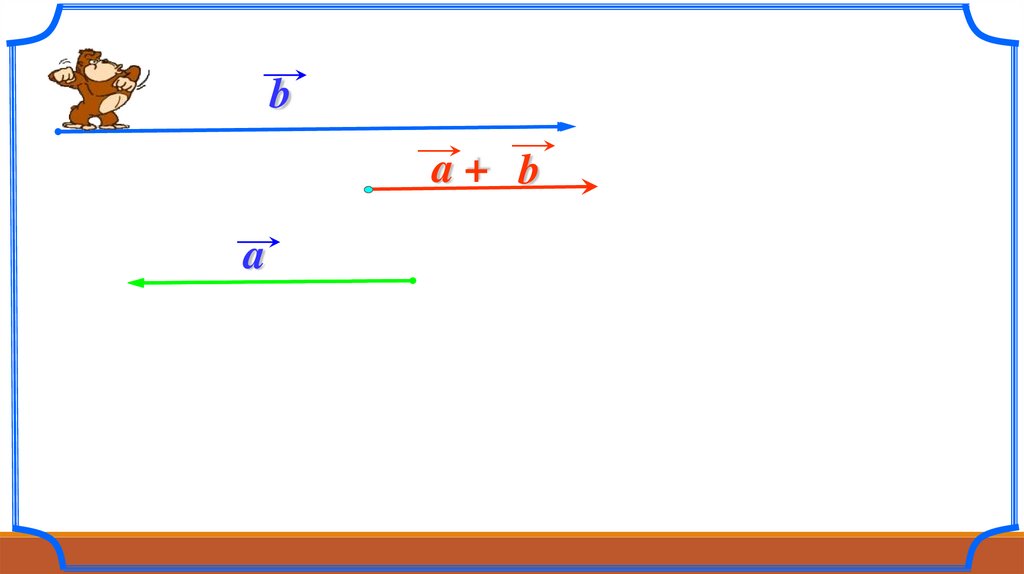
53.

b
a+ b
a

54.

Векторлардың айырымы. Үшбұрыштар ережесі.
a – b = a +(– b)
-b
b
-b
a
a
a- b

55.

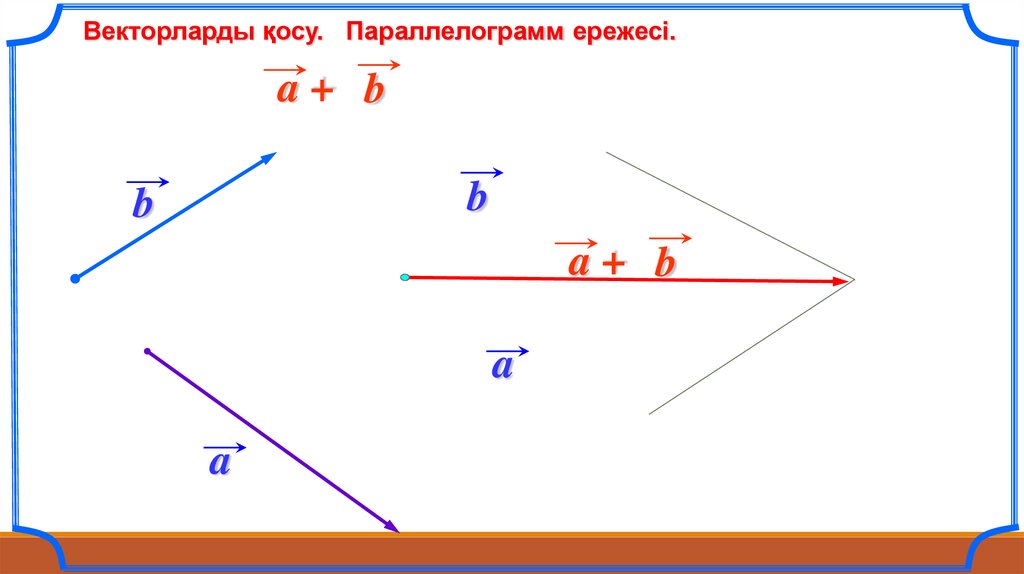
Векторларды қосу. Параллелограмм ережесі.
a+ b
b
b
a+ b
a
a

56.

векторларды қосу.
үшбұрыштар ережесі
АВ + ВС
=
АС
АО + ОР =
АР
MN + NR =
MR
MK + KM =
MM = 0
MK + OM =
OM + MK
= OK
MF - SF =
MF + FS
= MS
RO - RM =
RO + MR
= MR + RO
= MO

57.

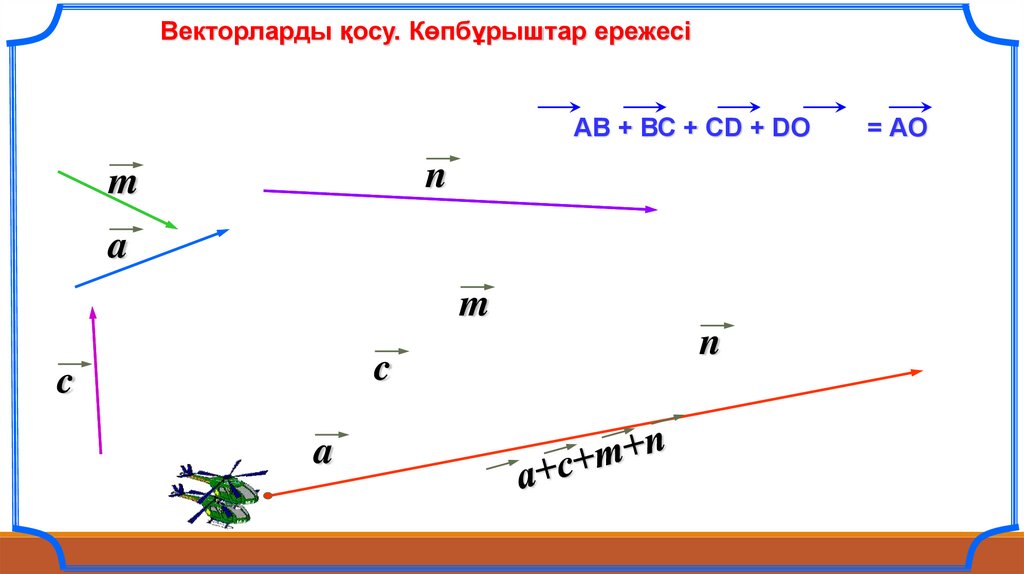
Векторларды қосу. Көпбұрыштар ережесі
АВ + ВС + СD + DO
n
m
a
m
c
c
a
n
= АO

58.

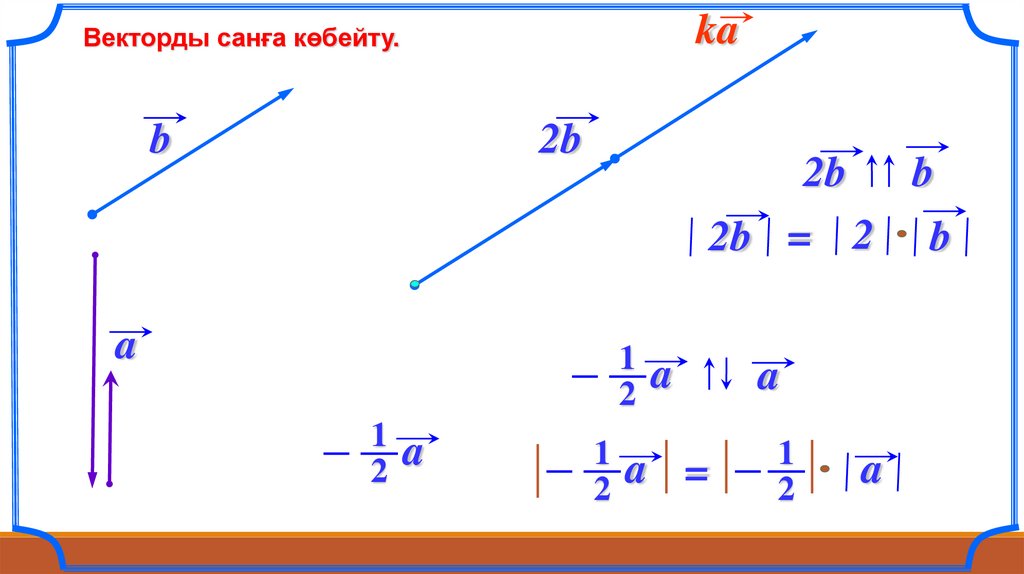
ka
Векторды санға көбейту.
b
2b
a
1
a
2
1
a
2
1
a
2
2b
b
2b = 2
b
a
=
1
2
a

59.

60.

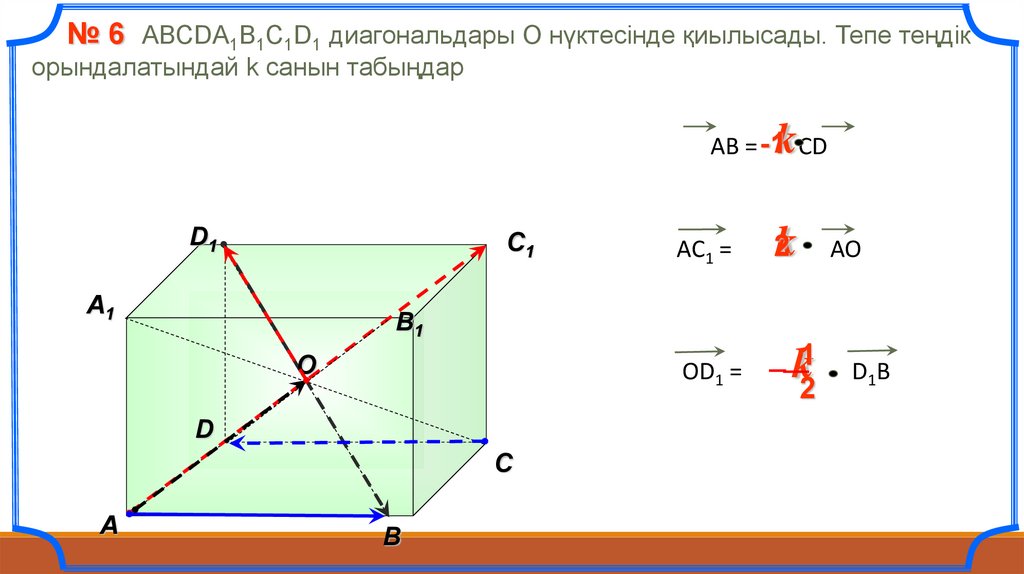
№ 6 АВСDА1В1С1D1 диагональдары О нүктесінде қиылысады. Тепе теңдік
орындалатындай k санын табыңдар
k
АВ = -1 СD
D1
C1
A1
2k
AO
B1
O
OD1 =
D
C
A
АC1 =
B
k12
D1B

61.

62.

63.

64.

Сабақтың тақырыбы
Кеңістіктегі тікбұрышты
координаталар жүйесі
10.4.5 - кеңістіктегі тікбұрышты координаталар жүйесі анықтамасын білу және оны
кескіндей алу;

65.

Кеңістіктегі координаталар
жүйесін XVIII ғасырда
неміс,орыс математигі
Леонард Эйлер
енгізген.

66.

67.

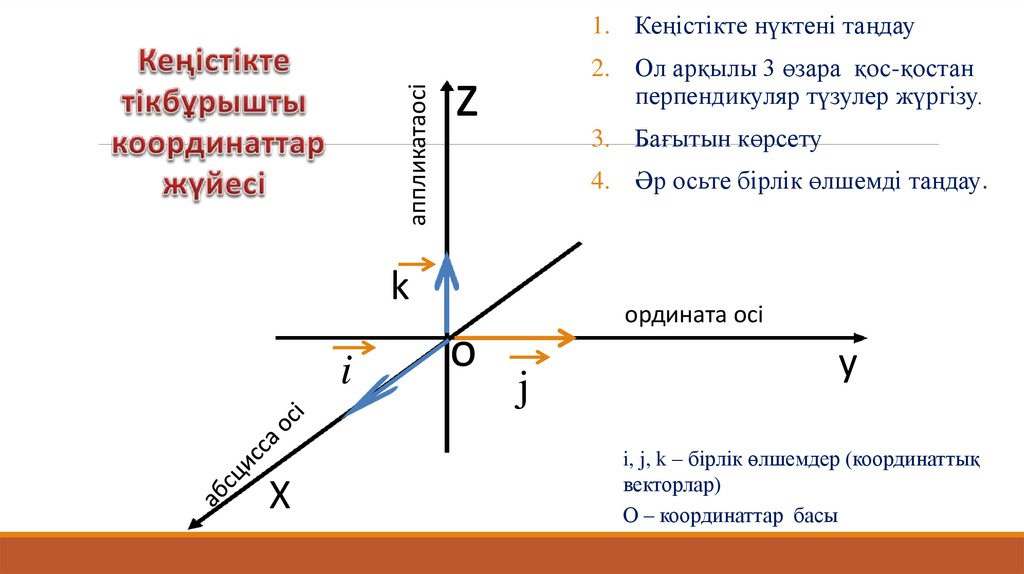
аппликатаосі
1. Кеңістікте нүктені таңдау
2. Ол арқылы 3 өзара қос-қостан
перпендикуляр түзулер жүргізу.
z
3. Бағытын көрсету
4. Әр осьте бірлік өлшемді таңдау.
k
i
X
o
ордината осі
j
у
i, j, k – бірлік өлшемдер (координаттық
векторлар)
О – координаттар басы

68.

69.

Бірлік вектор немесе орт деп ұзындығы бірге тең және бір координаттар
осі бойымен бағытталған векторды айтады.
i⃗ , j⃗ , k⃗ векторлары координаттық векторлар деп аталады. Кез-келген
векторды координаталық векторларға жіктеуге болады.

70.

Жіктелу коэффициенттері тек бір жолмен анықталады және берілген
координаттар жүйесіндегі a⃗ вектордың координаттары деп аталады.
•x осі бойымен бағытталған бірлік вектор i⃗ таңбасымен белгіленеді.
•y осі бойымен бағытталған бірлік вектор j⃗ таңбасымен белгіленеді.
•z осі бойымен бағытталған бірлік вектор k⃗ таңбасымен белгіленеді.

71.

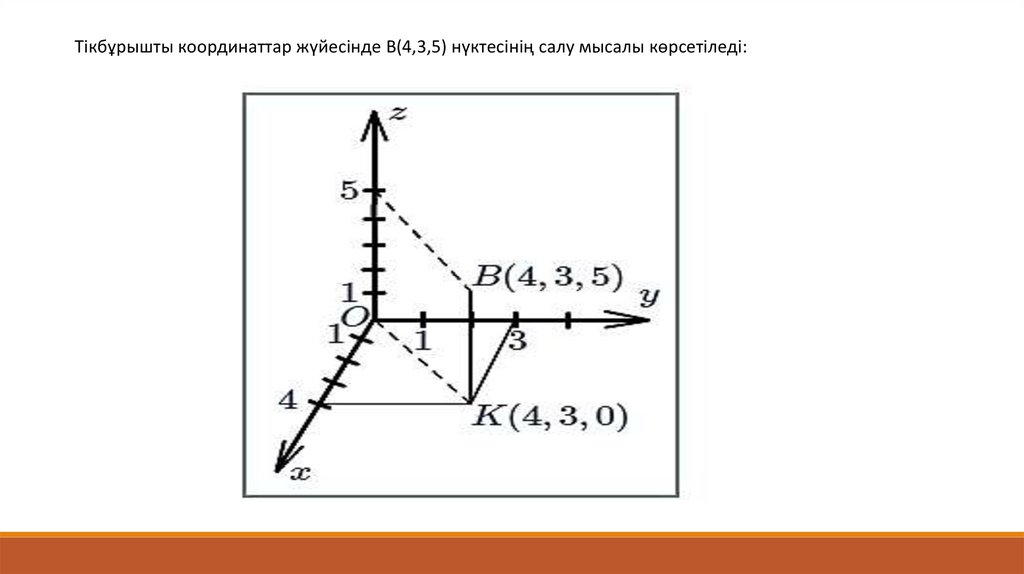
Тікбұрышты координаттар жүйесінде B(4,3,5) нүктесінің салу мысалы көрсетіледі:

72.

Тапсырма

73.

74.

3-есеп: А(1; 0; 0), В(0; -2; 0); С(0; 0; 7) координаталарымен
берілген кеңістіктік үшбұрышы мен жеке жатқан Д (1; -2; 7)
нүктесін координаталық осьте салыңыздар
Өз бетімен жұмыс. M(3;1;2) нүктесі берілген. Келесі
жағдайларда берілген нүктелердің координаталарын
табыңыздар: а) координаталар басына қатыста М нүктесіне
симметриялы орналасқан К нүктесінің; б) K нүктесіне
қатысты М нүктесіне симметриялы Р нүктесінің . Барлық
нүктелерді координаталық жазықтықта кескіндеңіздер.

75.

Рефлексия

76.

Сабақтың тақырыбы
Кеңістіктегі тікбұрышты
координаталар жүйесі
10.4.5 - кеңістіктегі тікбұрышты координаталар жүйесі анықтамасын білу және оны
кескіндей алу;
10.4.6 - кеңістіктегі нүктені оның координаталары
бойынша тікбұрышты координаталар жүйесінде
кескіндеу;

77.

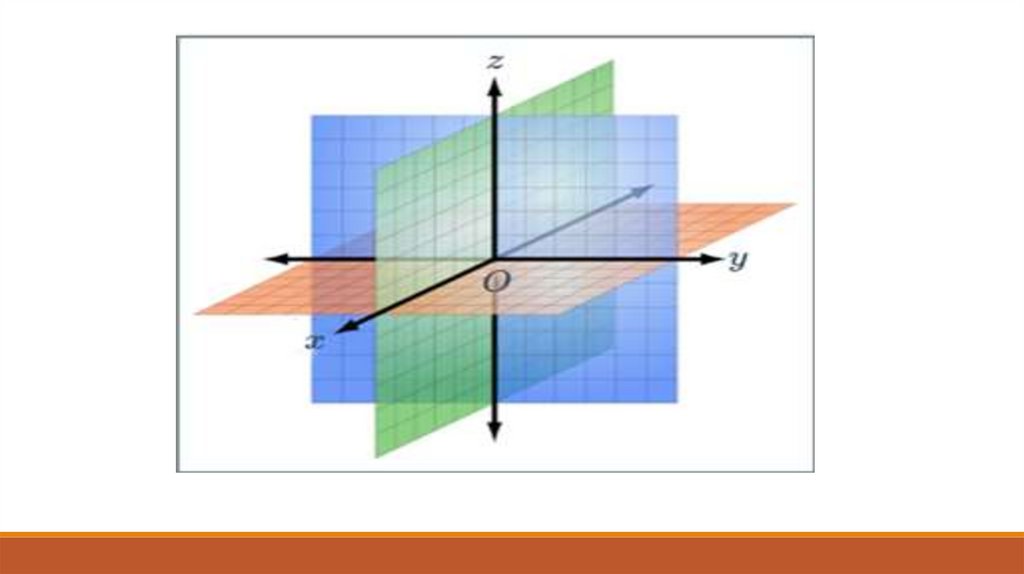
1-ші мәселелік сұрақ: Кеңістікте тікбұрышты координаттар жүйесін
қалай беруге болады?
Кеңістікте нүктені таңдау
Ол арқылы 3 өзара қос-қостан
перпендикуляр түзулер жүргізу.
Бағытын көрсету
Әр осьте бірлік өлшемді таңдау

78.

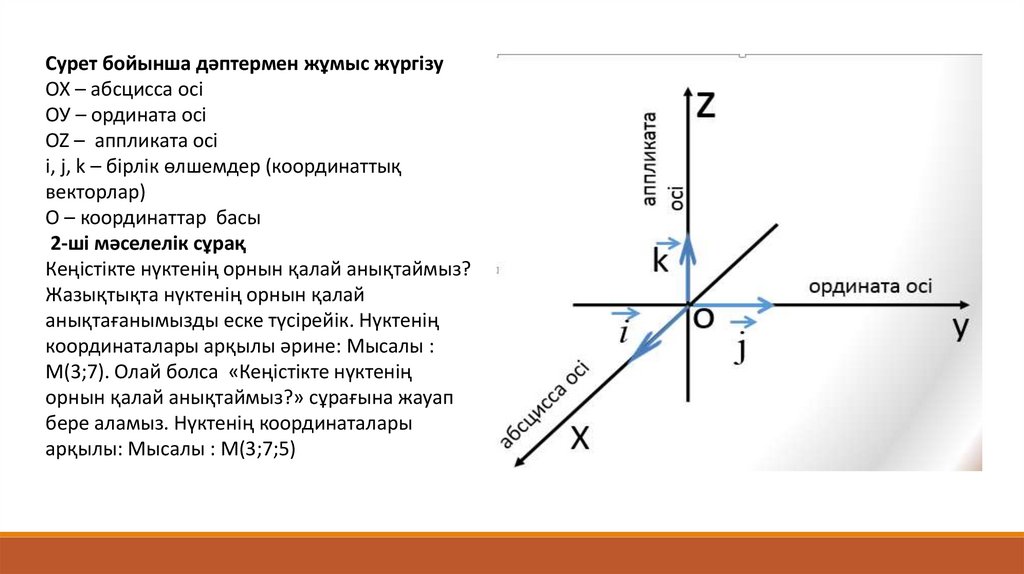
Сурет бойынша дәптермен жұмыс жүргізу
ОХ – абсцисса осі
ОУ – ордината осі
OZ – аппликата осі
i, j, k – бірлік өлшемдер (координаттық
векторлар)
О – координаттар басы
2-ші мәселелік сұрақ
Кеңістікте нүктенің орнын қалай анықтаймыз?
Жазықтықта нүктенің орнын қалай
анықтағанымызды еске түсірейік. Нүктенің
координаталары арқылы әрине: Мысалы :
М(3;7). Олай болса «Кеңістікте нүктенің
орнын қалай анықтаймыз?» сұрағына жауап
бере аламыз. Нүктенің координаталары
арқылы: Мысалы : М(3;7;5)

79.

Есеп шығару.
№1,2 есептерді оқушылар мұғаліммен бірге талдап
шығарады.
А(3;-1;0), В(0;0;-7), С(2;0;0), D(-4;0;3), Е(0;-1;0), Ғ(1;2;3),
G(0;5;-7) және H(- ; ; 0;) нүктелері берілген. Бұл
нүктелердің қайсысы:
а) абсциссалар осінде;
б) ординаталар осінде;
в) аппликаталар осінде;
г) Оху жазықтығында;
д) Оуz жазықтығында;
е) Охz жазықтығында жатады?

80.

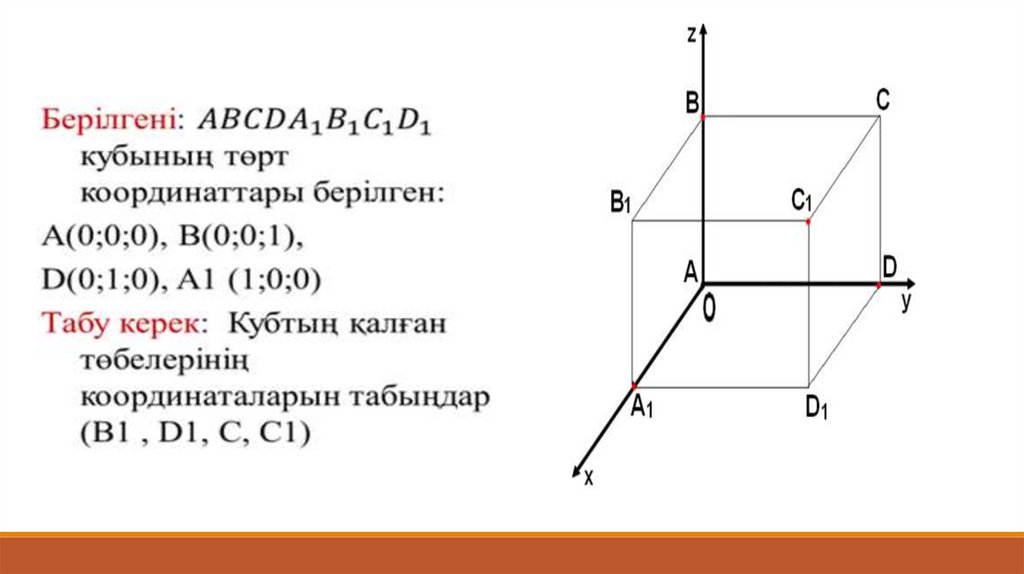
№2. Берілген нүктелерді кеңістікте тікбұрышты координаттар жүйесінде кескіндеңіз:

81.

№3. Берілген А(-4; 0; 0), B(5; -3; 0), С(0; 2; 0),
D(4; -6; 0), Е(0; 0; -10), F(0; 9; -7) нүктелерінің
ішінен а) Оx осінде; ә) Оy осінде; б) Оxy
жазықтығында; в) Оyz жазықтығында
жататын нүктелерді анықтаңдар

82.

Сабақтың тақырыбы
Кеңістіктегі вектордың координаталары
10.4.11 - вектордың координаталары ұғымын білу, вектор координаталарын бірлік
векторлар бойынша жіктеп таба білу;
10.4.13 - координаталарымен берілген векторларды
қосуды және векторды санға көбейтуді орындау;

83.

Вектордың координаталары.
А1(х1; у1; z1)
А2(x2; y2; z2)
A1А2 = {x2 – x1; y2 – y1; z2 – z1}

84.

1. МК векторының координатасын тап,
егер
М(10; -4; 2), К(16; 2; -5)
МК {16 – 10; 2 – (-4); -5 – 2}
ж:: М К { 6; 6; -7}

85.

Вектор ұзындығы
(модульі)
a {x; y; z}
ІaІ = √ x² + y² + z²

86.

2. Вектордың ұзындығын тап
а { - 5; 1; 2}
ІаІ = √ 25 + 1 + 4
жауап: √30
= √30

87.

3. n-нің қандай мәнінде екі вектор тең болады?
а{4; 2n - 1; -1} , в{4; 9 – 3n; -1}
2n – 1 = 9 – 3n
2n + 3n = 9 + 1
5n = 10
n=2
ж: n = 2

88.

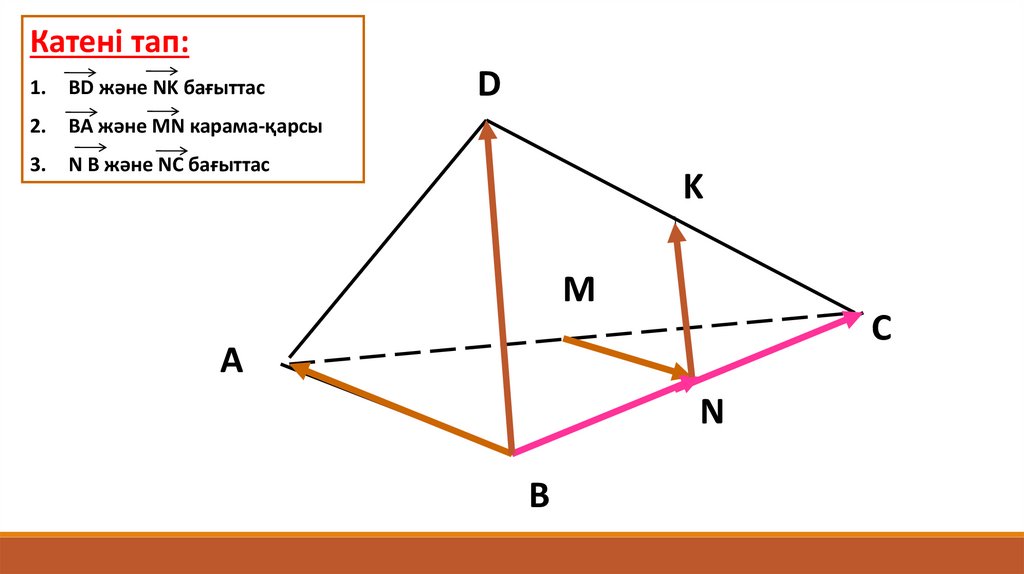
Катені тап:
1.
BD және NK бағыттас
2.
ВА және MN карама-қарсы
3.
N В және NC бағыттас
D
K
M
С
А
N
В

89.

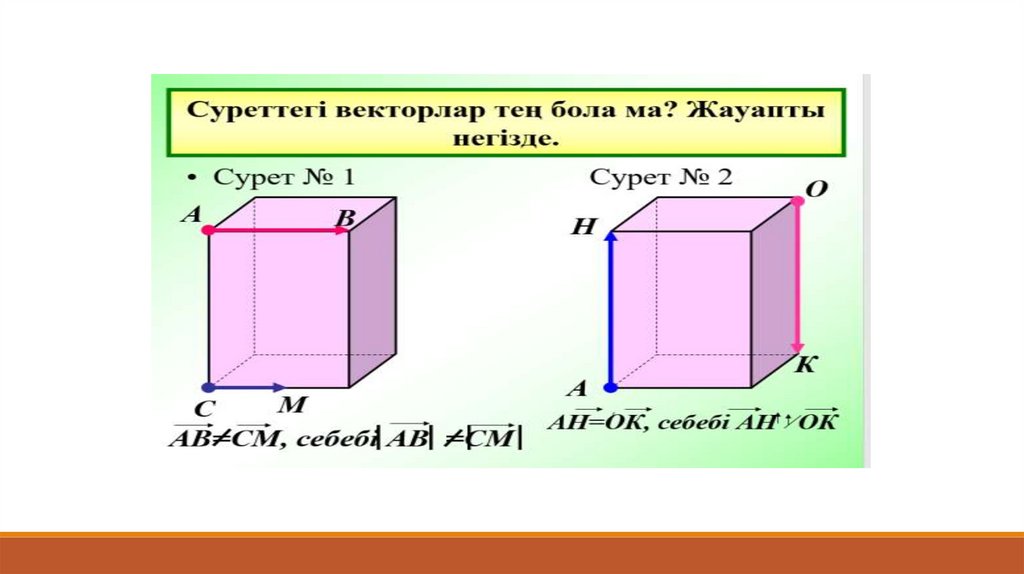
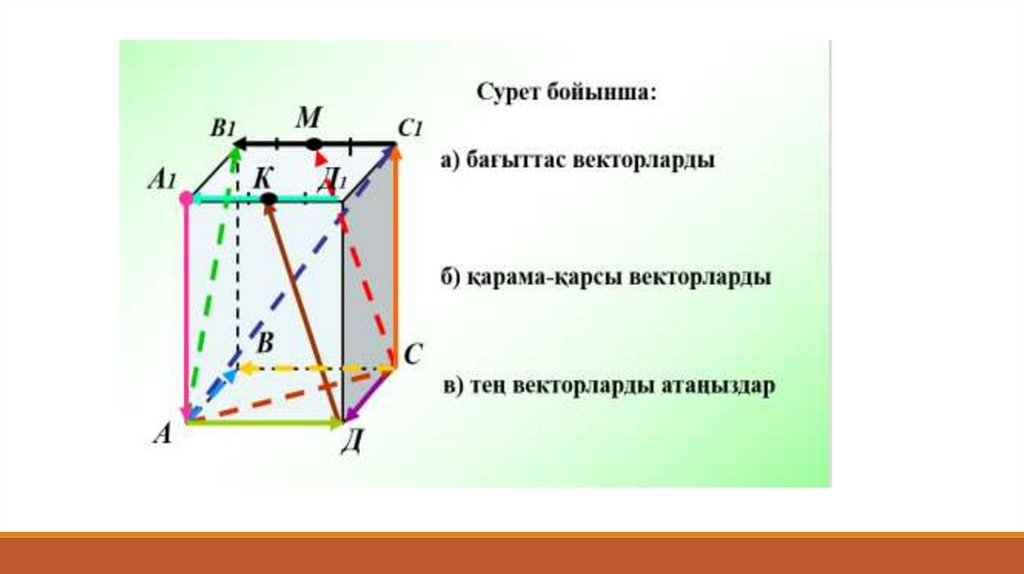
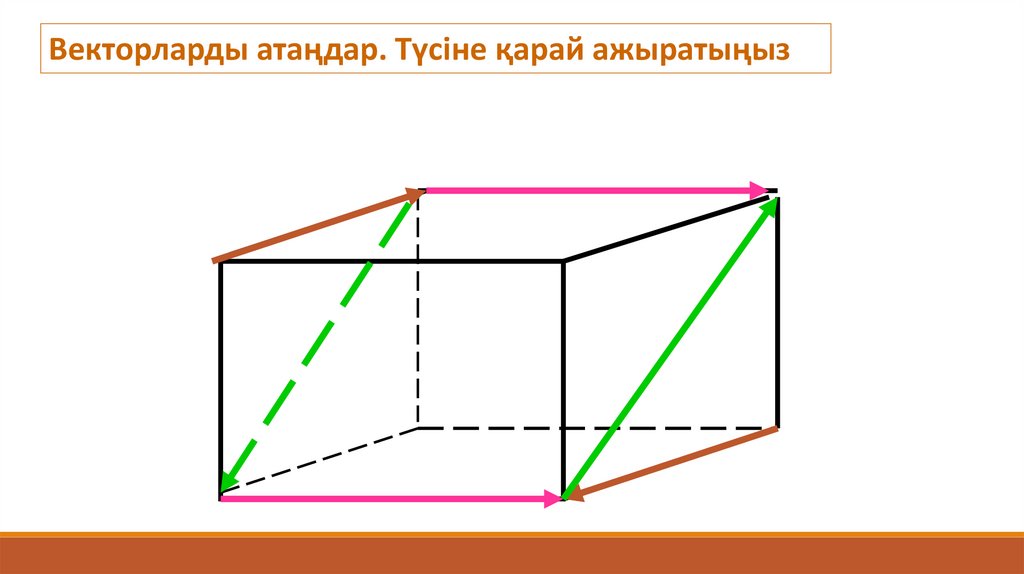
Векторларды атаңдар. Түсіне қарай ажыратыңыз

90.

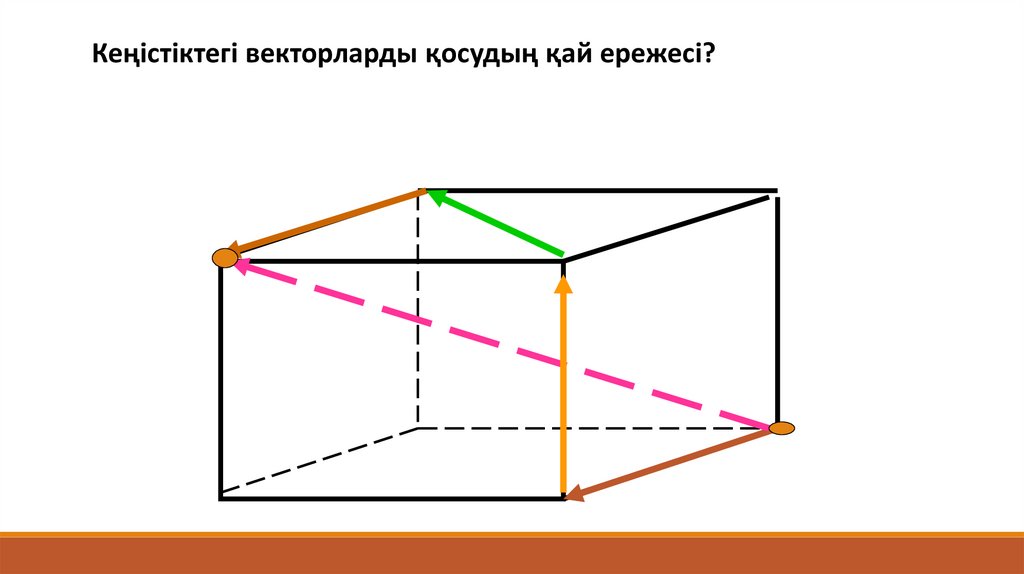
Кеңістіктегі векторларды қосудың қай ережесі?

91.

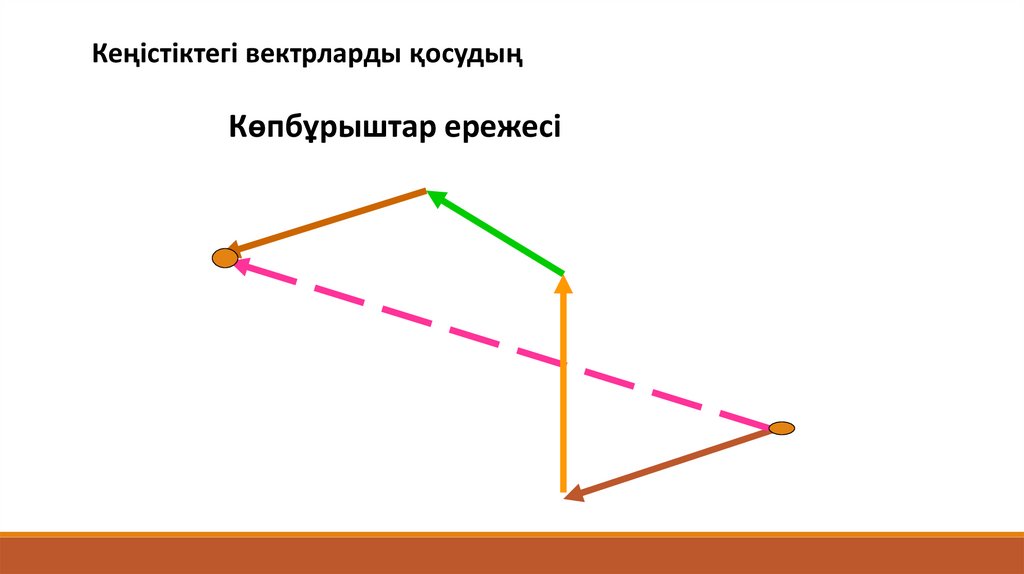
Кеңістіктегі вектрларды қосудың
Көпбұрыштар ережесі

92.

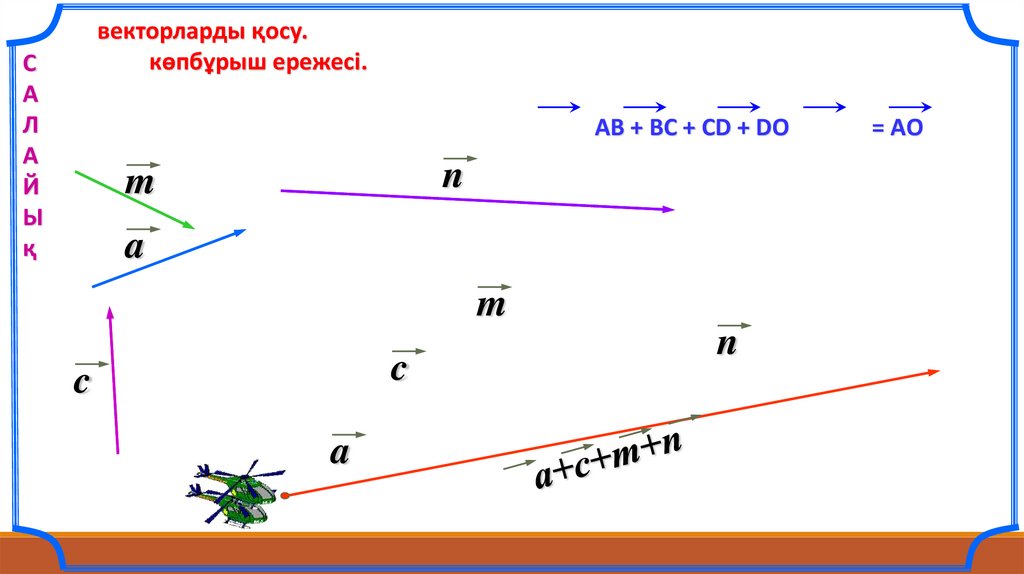
векторларды қосу.
көпбұрыш ережесі.
С
А
Л
А
Й
Ы
қ
АВ + ВС + СD + DO
n
m
a
m
c
c
a
n
= АO

93.

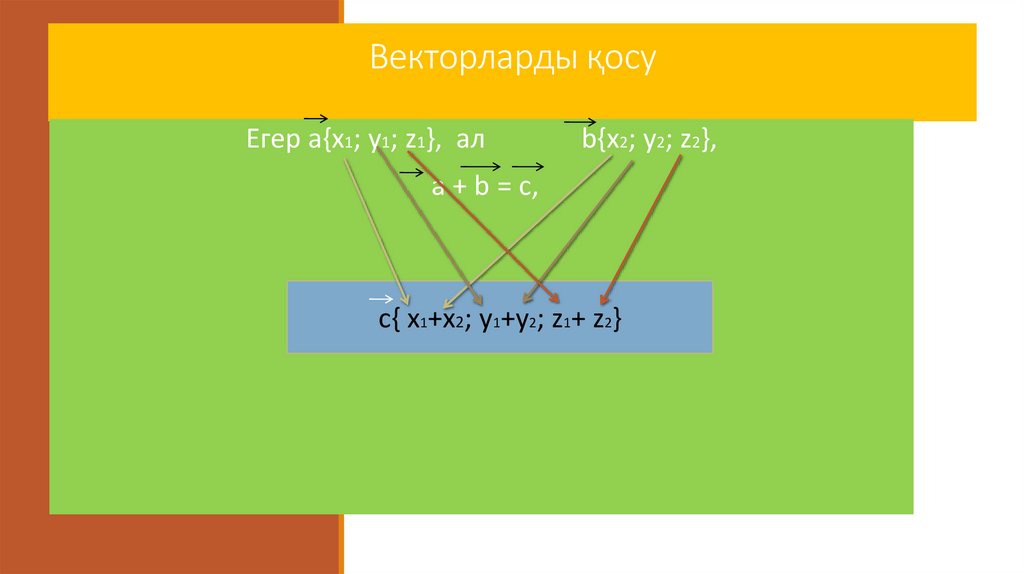
Векторларды қосу
Егер a{х1; у1; z1}, ал
b{х2; у2; z2},
a + b = c,
c{ х1+х2; у1+у2; z1+ z2}

94.

5. Векторлардың қосындысын тап
а b, егер а{2; 3; -1}, b{3; -2; 0}
ж\е
шешуі:
а + b = {2 + 3; 3 – 2; -1 + 0} = {5; 1; -1}
жауап: {5; 1; -1}

95.

Векторлардың айырымы
b
a
a b a ( b)
b
a b
a

96.

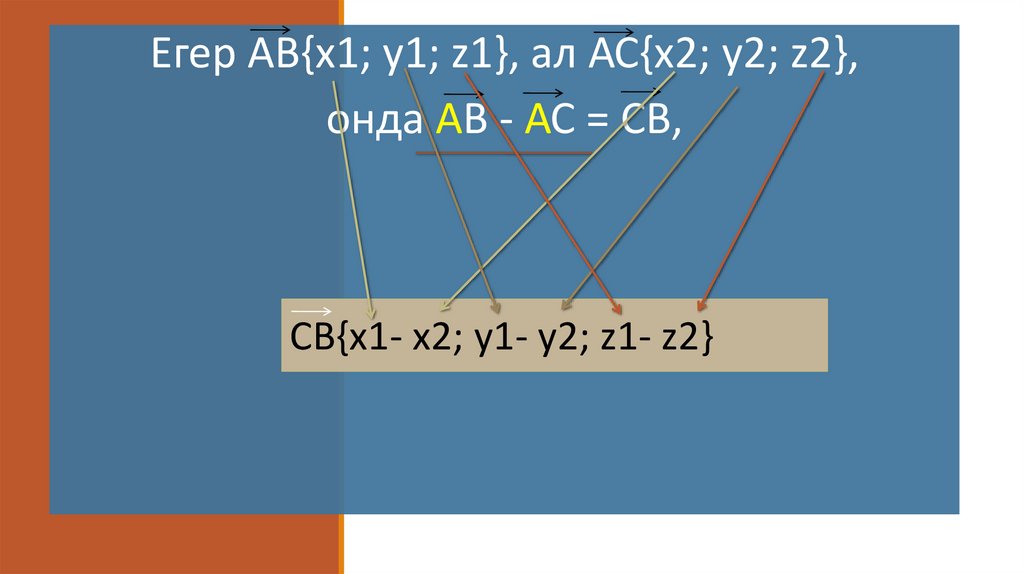
Егер АВ{х1; Разность
у1; z1},векторов
ал АС{х2; у2; z2},
онда АВ - АС = СВ,
CB{х1- х2; у1- у2; z1- z2}

97.

6. Векторлардың айырмасын тап
егер a{3; 7; 10}, b{1; 9; -6}
шешуі:
a – b {3 – 1; 7 – 9; 10 + 6} = {2; -2; 16}
жауап: {2; -2; 16}

98.

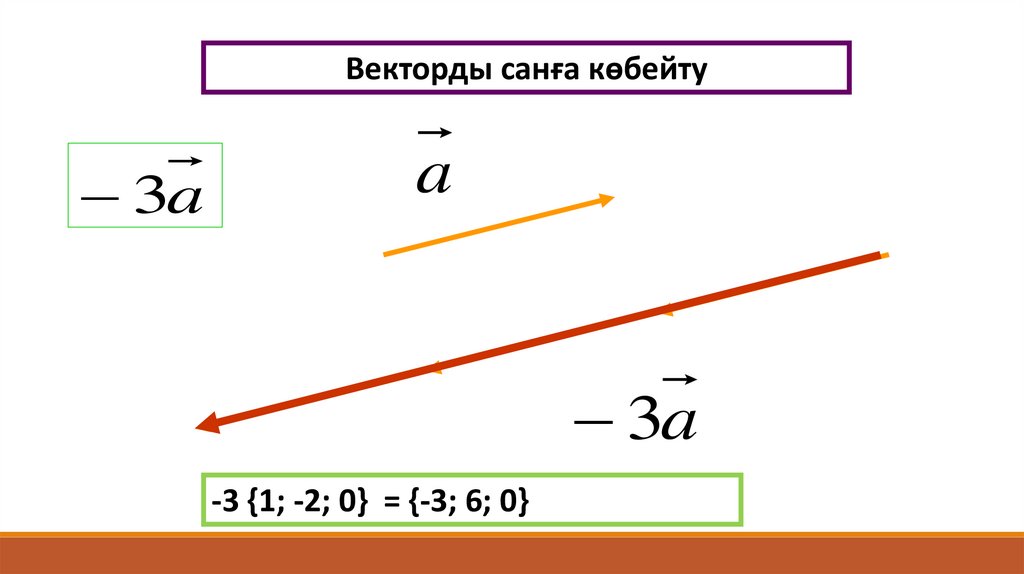
Векторды санға көбейту
3a
a
3a
-3 {1; -2; 0} = {-3; 6; 0}

99.

№7. с векторының координаталарын тап
с = 2а -3b, если а{7; -3; 0} ; b{4; 1; -2}
шешуі:
2а{14; -6; 0} 3b{12; 3; -6}
2а - 3b {14 – 12; -6 -3; 0 – (-6)} = {2; -9; 6}

100.

№8. 3а векторының ұзындығын тап,
егер а{4; -4; 2} болса
Бірінші тәсіл
3а {12; -12; 6}
І3аІ = √144+ 144+ 36 =
= √324 =18
Екінші тәсіл
а {4; -4; 2}
ІаІ = √16+ 16+ 4 = √36 = 6
3 ІаІ = 3 ·6 = 18
І3аІ = 18

101.

Векторлардың коллинеарлық шарты:
a {х1; у1; z1} b{x2; y2; z2}
х1 у1 z 1
=
=
x2 y2
z2

102.

№9. m және n нің қандай мәнінде векторлар
коллинеар болады? а{4; -1; n} және
с{8; m; 2}
Пропорция құрамыз:
m = (-1 · 8): 4 = -2;
4
-1
n
8
m
2
n = (4· 2): 8 = 1;
жауап: m = -2 ; n = 1.