Similar presentations:
Инженерно - геодезические опорные сети
1.
Лекция 3.ИНЖЕНЕРНО-ГЕОДЕЗИЧЕСКИЕ
ОПОРНЫЕ СЕТИ
2.
1. Назначение, виды и особенностипостроения опорных геодезических сетей.
2.
Системы
координат
и
высот,
применяемые в инженерно-геодезических
работах
3.
1. Назначение, виды и особенностипостроения опорных геодезических
сетей.
Опорные сети создаются для обеспечения всех видов инженерно-геодезических
работ.
Их пункты хранят на территории работ
плановые координаты и высоты.
4.
Эти сети служат основой:– для производства топографических съемок
при изысканиях;
– для выполнения различных работ на
территории городов;
–
при
составлении
исполнительной
документации;
– для выполнения разбивочных работ при
строительстве зданий и сооружений;
– для наблюдений за деформациями
оснований сооружений и самих сооружений.
5.
Инженерно-геодезическиеплановые
и
высотные опорные сети представляют собой
систему
геометрических
фигур,
вершины
которых
закреплены
на
местности
специальными знаками.
Плановые и высотные опорные сети создают
в соответствии с заранее разработанным
проектом производства геодезических работ.
При составлении этого проекта собирают
сведения,
относящиеся
к
опорным
геодезическим сетям во всех организациях,
производящих
работы
на
территории
предстоящего
строительства,
а
также
специальных геодезических организациях.
6.
По собранным материалам составляютсхему
расположения
пунктов
ранее
выполненных опорных сетей всех классов
и разрядов в пределах территории
предстоящих работ.
В геодезической практике достаточно
часто сеть создают заново,
даже при
наличии близкорасположенных пунктов
ранее созданных сетей.
Поступают так с целью обеспечения
повышенной
точности
определения
взаимного положения пунктов.
7.
Инженерно-геодезическиеопорные
сети обладают рядом
характерных
особенностей:
а) сети часто создаются в условной
системе координат;
б)
форма
сети
определяется
обслуживаемой территорией или формой
объектов;
8.
в) сети имеют ограниченные размеры,часто с незначительным числом фигур
или полигонов;
г) короткие длины сторон;
д) к пунктам сети предъявляются
повышенные требования по стабильности
их положения;
е)
неблагоприятные
условия
наблюдений.
9.
Выборвида
построения
и
его
конфигурация зависит от следующих
причин:
– типа объекта, его формы и
занимаемой площади;
– назначения сети;
– физико-географических условий;
– требуемой точности;
– наличия измерительных средств у
исполнителя.
10.
Так, триангуляцию применяют на объектах,значительных по площади и протяженности,
проектируемых
в
открытой
пересеченной
местности.
Полигонометрию используют на закрытой
местности или застроенной территории.
Линейно-угловые сети – при необходимости
создания сетей повышенной точности.
Трилатерацию – на небольших объектах, где
требуется высокая точность.
Строительные сетки – на промышленных
площадках.
11.
Высотные опорные сети, в основном,создают
методом
геометрического
нивелирования в виде одиночных ходов
или полигонов, проложенных между
исходными реперами.
В отдельных случаях, при наличии
электронных
тахеометров,
может
применяться способ тригонометрического
нивелирования.
12.
2. Системы координат и высот,применяемые в инженерно-геодезических
работах
Государственные геодезические сети до их
уравнивания должны быть отнесены на какую-то
поверхность относимости (референц-эллипсоид
Красовского).
Для этого в сетях 1 и 2 класса в измеряемые
элементы вводятся редукционные поправки.
Проектирование всех последующих сетей
сгущения осуществляется на единой поверхности
относимости.
13.
Редукционныепоправки
вводят
при
выполнении геодезических измерений для того,
чтобы получить результаты без искажений.
Существуют две поправки:
поправка за отнесение базисной стороны на
поверхность относимости;
поправка в длину линии при переходе на
плоскость.
В
качестве
поверхности
относимости
принимают средний уровень строительной
площадки.
В гражданских зданиях - это уровень первого
этажа, на трассах метрополитена - уровень оси
тоннеля или головок рельсового пути и др.
14.
В целях картографирования геодезические сетипроецируются на плоскость в проекции ГауссаКрюгера (на территории стран СНГ).
В инженерно-геодезических работах применяют
государственные системы координат (СК-42, СК63, СК-95) и местные системы координат.
Для современных промышленных комплексов
применяется
частная
(условная)
система
координат, начало координат которой не совпадает
с началом государственной системы координат, а
ее
оси
развернуты
относительно
осей
государственной системы координат.
15.
Высотные сети (государственные и инженерногеодезические) проектируют и создают в единойсистеме высот.
За начало высот принят средний уровень
Балтийского моря.
Этот уровень отмечен горизонтальной чертой
на медной металлической пластине, укрепленной
в устое моста через обводной канал в
Кронштадте.
Основным методом создания высотных сетей
является геометрическое нивелирование.
16.
При определении разности высот поверхностиземли методом геометрического нивелирования
возникает
некоторая
неопределенность
в
значении превышений вследствие того, что
уровенные поверхности различных точек Земли
не параллельны между собой.
Это
обусловлено
неравномерностью
распределения масс земной коры и суточным
вращением Земли.
В
зависимости
от
принципа
учета
непараллельности
уровенных
поверхностей
различают нормальные, динамические и
ортометрические высоты.
17.
По предложению М.С. Молоденского, принятасистема нормальных высот.
Нормальные высоты точек отсчитываются по
направлениям отвесных линий от поверхности
квазигеоида, которая близка к поверхности
геоида.
Динамическую систему высот целесообразно
применять для инженерно-технических расчетов,
связанных с учетом работы, совершаемой в
гравитационном поле Земли, в метеорологии.
Для вычисления результатов нивелирования
при создании государственных геодезических
сетей динамические высоты не применяются.
18.
ТЕМА:«ОПРЕДЕЛЕНИЕ
ДОПОЛНИТЕЛЬНЫХ ПУНКТОВ»
19.
1. Снесение координат с вершинзнака на землю.
2. Прямая засечка.
3. Обратная засечка.
4. Линейная засечка.
20.
1. Снесение координат с вершин знака наземлю.
Дополнительные пункты определяются наряду
со съемочной сетью в основном для сгущения
существующей геодезической сети пунктами
съемочного обоснования.
Они
строятся
прямыми,
обратными,
комбинированными
угловыми, а при
наличии
электронных
дальномеров
–
линейными засечками и лучевым методом.
В некоторых случаях дополнительный пункт
определяется
передачей
(снесением)
координат с вершины знака на землю.
21.
Припривязке
полигонометрического
(теодолитного) хода к пункту триангуляции,
на котором нельзя установить прибор,
выбирают на земле вблизи этого пункта А
(на расстоянии 50–100 м от него) точку Р.
в таком месте, чтобы, кроме пункта А
были видны два удаленных пункта исходной
сети В и С (один из них необходим для
контроля) и удобно было измерить два
базиса для определения неприступного
расстояния АР.
22.
BC
y’
s
s`
A
f’
f
g’ g
b’ b ’2
b2
d’
d b
b ’1 b 1
P
y
23.
Второй базис b/ и углы при нем β'1, β'2,используют для контроля определения
расстояния АР и повышения точности
получения окончательного его значения.
Рассмотрим решение задачи по этапам.
1. Вычисление дирекционных углов (АВ),
(АС) и расстояний АВ=s, AC=s'.
Имея координаты пунктов А и В, вычисляют
дирекционный угол (АВ)
YB YA
(1)
( AB) arctg
XB XA
24.
и расстояние АВ = sYB YA
XB XA
s
. (2)
sin( AB) cos( AB)
Если полученные значения s различаются на две
единицы последнего знака, то за окончательное
принимают среднее арифметическое.
Точно так же определяют дирекционный угол
(АС) и расстояние АС.
Иногда дирекционные углы (АВ), (АС) и
расстояния АВ, АС бывают известны из
материалов исходной геодезической сети.
25.
2. Вычисление расстояния АР=d.Недоступное расстояние АР = d определяют дважды:
b sin 2
b
sin
2
d1
; d2
;
sin
sin
где
γ = 1800 – (β1 + β2),
γ' = 1800 – (β'1 + β'2).
(3)
26.
1Разность |d1 – d2| не должна превышать 2d
T
1
– предельная относительная
где
T погрешность измерения базисов b
и b'.
За окончательное значение расстояния АР
принимают среднее арифметическое значение
d1 d 2
d
.
2
(4)
27.
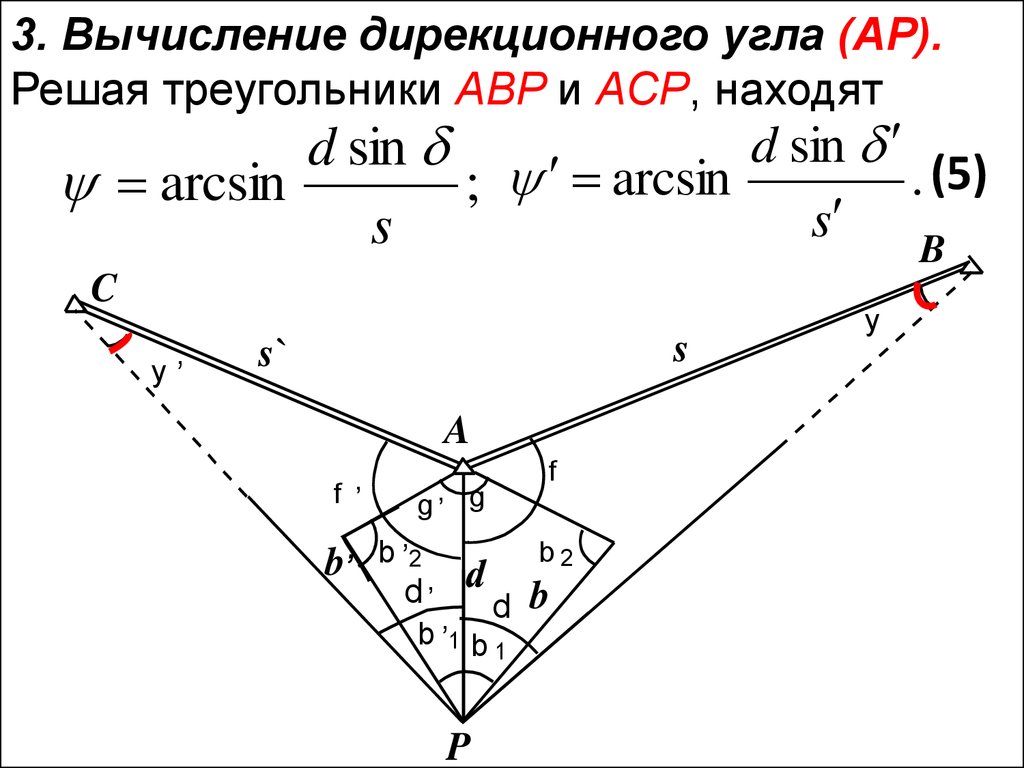
3. Вычисление дирекционного угла (AP).Решая треугольники ABP и ACP, находят
d sin
d sin
. (5)
arcsin
; arcsin
s
s
B
C
y’
s
s`
A
f ’
b’
f
g’ g
b ’2
b2
d’
d b
b ’1 b 1
P
y
28.
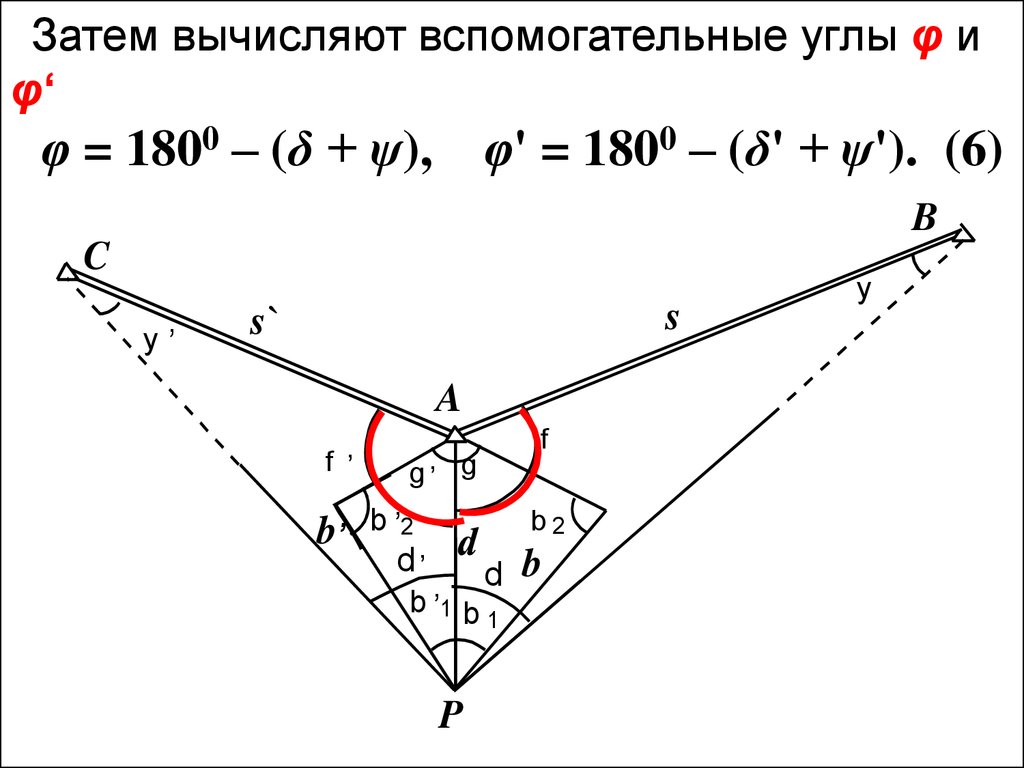
Затем вычисляют вспомогательные углы φ иφ‘
φ = 1800 – (δ + ψ),
φ' = 1800 – (δ' + ψ'). (6)
B
C
y’
s
s`
A
f ’
b’
f
g’ g
b ’2
b2
d’
d b
b ’1 b 1
P
y
29.
По этим углам определяют два значениядирекционного угла (AP)
(AP)1 = (АВ) + φ, (AP)2 = (АС) – φ‘. (7)
Расхождение между значениями (АР)1 и (АР)2
должно удовлетворять неравенству
( AP)1 ( AP)2 6m, (8)
где m – средняя квадратическая погрешность
измерения угла.
30.
4. Вычисление координат точки PПо расстоянию AP = d и дирекционному углу
(АР) находят, приращения координат
X 1 d cos( AP)1; Y1 d sin( AP)1
(9)
.
X 2 d cos( AP) 2 ; Y2 d sin( AP) 2
Затем вычисляют координаты точки Р
X 1 X A X 1; Y1 YA Y 1
. (10)
X 2 X A X 2 ; Y2 YA Y 2.
31.
Заокончательные
координат
принимают
арифметические значения
значения
средние
X1 X 2
Y
Y
1
2
X
; Y
. (11)
2
2
32.
5. Оценка точности положения точки Р.Средней квадратической ошибкой положения
точки
называется
средняя
величина
смещения
относительно
ее
точного
положения и определяемая в общем случае
соотношением
2
2 (12)
M m m .
x
y
Для данного случая можно использовать
формулу
2
2
mb 1 m
. (13)
M d
b 2
33.
2. Прямая засечка.Для решения прямой засечки,
заключающейся в определении
координат третьего пункта по
координатам
двух
исходных
пунктов и измеренным при них
углам,
предложено
много
различных формул.
34.
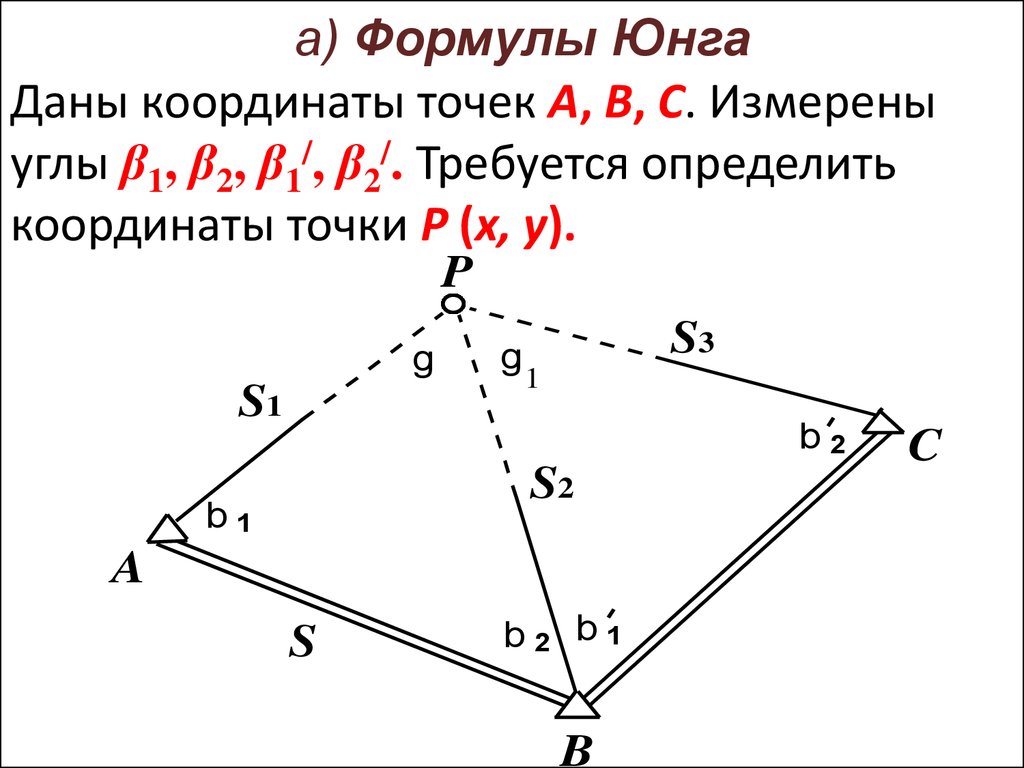
а) Формулы ЮнгаДаны координаты точек А, B, C. Измерены
углы β1, β2, β1/, β2/. Требуется определить
координаты точки P (x, y).
P
g
S1
g
S3
1
b2
S2
b1
A
S
b2 b1
B
C
35.
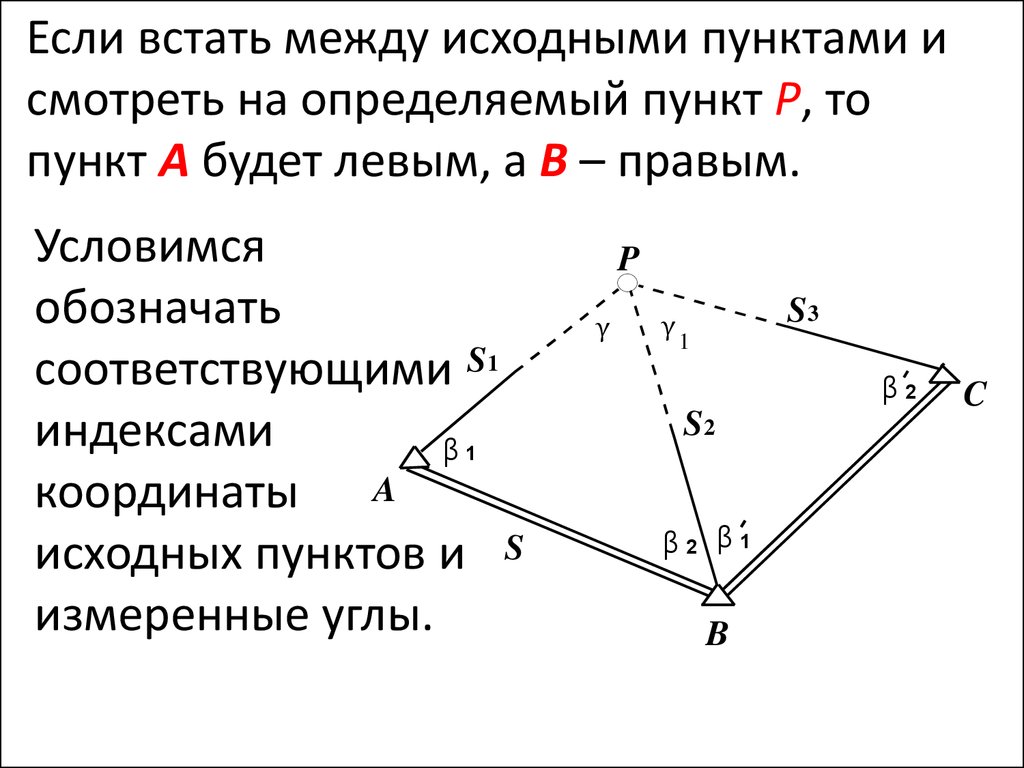
Если встать между исходными пунктами исмотреть на определяемый пункт P, то
пункт А будет левым, а В – правым.
Условимся
обозначать
соответствующими S1
индексами
β
координаты A
исходных пунктов и S
измеренные углы.
P
γ
S3
γ1
β2
S2
1
β2 β1
B
C
36.
Тогда формулам Юнга можно придатьследующий вид:
X ctgП Х П ctg У У П (14)
XP
,
сtg сtgП
У ctgП У П ctg Х Х П (15)
УP
,
сtg сtgП
где Λ и П – значения углов при левом и
правом пунктах (Λ= 1, П = 2).
37.
В целях контроля находят уголγ=1800– 1 – 2,
а затем по координатам пункта В (левый)
и координатам пункта Р (правый) по
формулам (14) и (15) вычисляют
координаты пункта А, которые должны
совпадать с заданными.
Для полного контроля полевых измерений
и выписки исходных данных нужно
решить, задачу, используя координаты
точек В и C.
38.
Расхождениемежду
абсциссами
и
ординатами при первом и втором решении
должны удовлетворять условию
r
X ' X " Y ' Y "
2
2
3M r ; (16)
где Мr – среднее квадратическое
расхождение в положении пункта Р из двух
решений.
2
2
В свою очередь, M r M 1 M 2 ,
где М1 и М2 – СКО положения пункта Р из
первого и второго решения.
39.
СКО положения пункта Р, определяемогопрямой засечкой, вычисляется по формуле
m s s
M
, (18)
sin
2
1
2
2
где m – СКО измерения углов;
s1 и s2 – расстояние от исходных пунктов
до определяемого (можно вычислить по
координатам точек);
– угол засечки.
40.
б) Формулы Гаусса.При определении точки прямой
засечкой может не быть видимости
между смежными точками А, В и С.
В таком случае целесообразно
пользоваться формулами Гаусса, в
которые входят дирекционные углы
направлений с данных пунктов на
определяемый.
41.
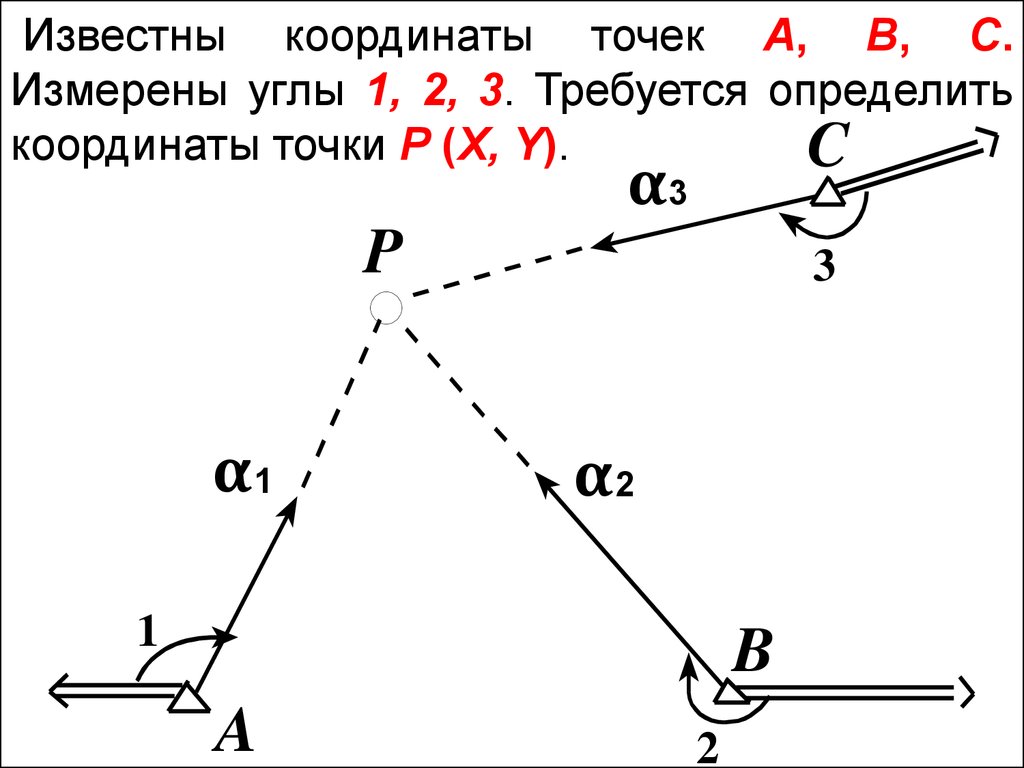
Известны координаты точек А, B, C.Измерены углы 1, 2, 3. Требуется определить
координаты точки P (X, Y).
C
α3
P
α1
3
α2
1
B
A
2
42.
По измеренным углам и дирекционнымуглам направлений на другие исходные
пункты, находим дирекционные углы
направлений на определяемую точку α1, α2
и α3.
Y YA
,
Запишем соответствие tg 1
X XA
откуда
Y YA ( X X A )tg 1. (19)
Аналогично получим
Y YB ( X X B )tg 2 . (20)
43.
Найдем разностьYB YA X (tg 1 tg 2 ) X Atg 1 X Btg 2.
Отсюда
X Atg 1 X Btg 2 YB YA
X
. (21)
tg 1 tg 2
44.
Вместо (19) и (20) можно записатьY YA ( X X A )tg 1,
Y YB ( X X B )tg 2 .
(22)
(23)
45.
Нахождение ординат по двум формулам(22) и (23) позволяет проконтролировать
вычисления.
Таким образом, формулы (21), (22) и
(23) – формулы Гаусса для определения
координат.
Для контроля правильности полевых
измерений вычисляют координаты точки
Р вторично, используя другую пару
исходных
пунктов
В
и
С
и
соответствующие дирекционные углы.
46.
3. Обратная засечка(задача Потенота)
Сущность
обратной
засечки
заключается в определении положения
четвертого пункта (точки стояния) по
трем исходным.
Эта задача встречается при создании
съёмочных
сетей,
привязке
аэрофотоснимков, выносе проектов в
натуру и других случаях.
47.
На основе трех исходных пунктов задачарешается без контроля правильности
измерения углов и выборки исходных
данных. Поэтому на практике используют
четыре исходных пункта.
Точность определения положения пункта
обратной засечкой зависит от ошибок
измерения углов, ошибок исходных
данных
и взаимного расположения
пунктов.
Обратную
засечку
рекомендуется
делать с предвычислением точности.
48.
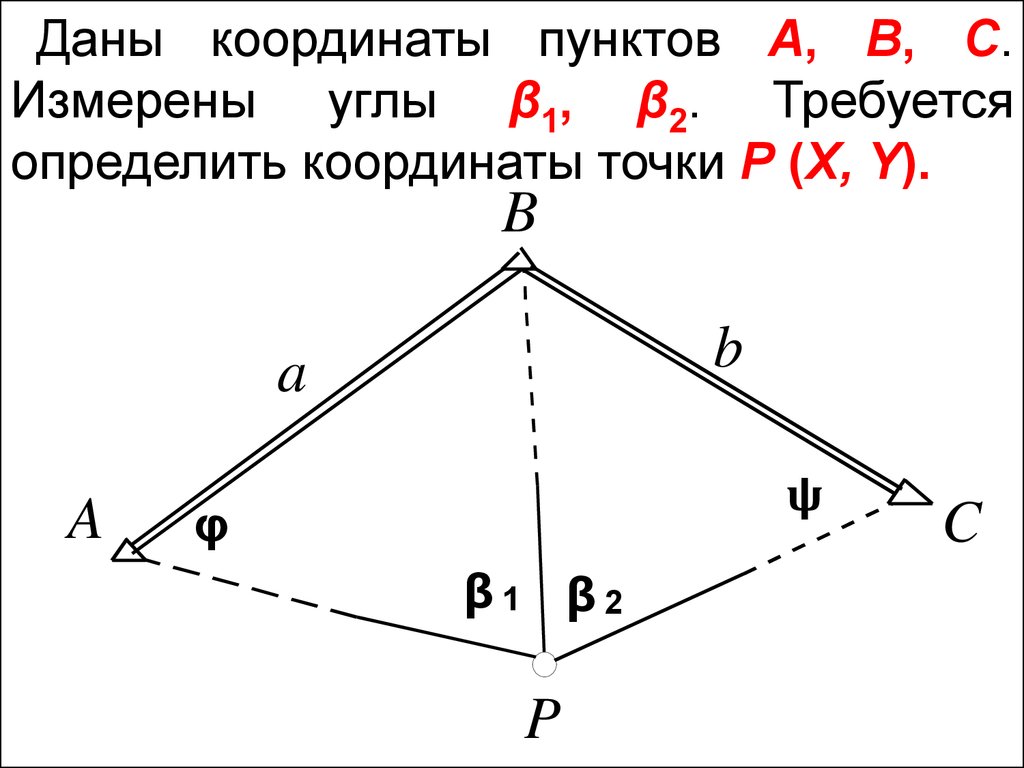
Даны координаты пунктов А, B, C.Измерены углы β1, β2. Требуется
определить координаты точки P (X, Y).
B
b
a
A
ψ
φ
β1 β2
P
C
49.
Вначале
решением
обратных
геодезических
задач
определим
дирекционные углы и длины исходных
линий:
YB YC
YB YA
( AB) arctg
; (CB) arctg
X B XC
XB XA
YB YA X B X A
2
2
a
( X B X A ) (YB YA ) ,
sin( AB) cos( AB)
YB YC X B X C
2
2
b
( X B X C ) (YB YC ) .
sin( CB) cos(CB)
50.
Далее задача сводится к определениюуглов φ и ψ.
Определим полусумму углов φ и ψ,
которую обозначим как А
1
1
0
( ) [360 1 2 (CB) ( AB)] A
2
2
Определим полуразность
которую обозначим через В
1
( ) B.
2
этих
углов,
51.
Определим диаметры описанных окружностей около треугольников ABP и BCP:b
a
.
Д1
, Д2
sin 2
sin 1
Выразим сторону ВР через Д1, Д2 и углы
φ и ψ.
BP Д1 sin ,
Откуда
BP Д 2 sin .
Д1 sin Д2 sin .
52.
Разделив две части этого равенствана Д1sin ψ, получим
.
Д 2 sin
Д1 sin
Образуем
пропорцию
обозначение N:
и
введем
Д 2 Д 1 sin sin
N.
Д 2 Д1 sin sin
53.
С учетом формул для определения Д1 и Д2b
a b
a
:
.
N
sin 2 sin 1 sin 2 sin 1
С учетом тригонометрических формул
2 cos
sin
sin sin
2
2 ctgAtgB N .
sin sin 2 sin cos
2
2
54.
Отсюда.
B arctg (NtgA)
Вычислив значения А и В, определим
углы φ и ψ
φ = А+ В,
ψ = А – В.
Далее определим длину линии АР
a
AP
sin( 1 )
sin 1
55.
Координаты точки Р:,
X P X A AP cos[( AB) ],
YP YA AP sin[( AB) ].
Для контроля координат точки Р можно
вычислить второй раз, используя формулы
b
CP
sin( 2 )
sin 2
X P X C CP cos[(CB) ],
YP YC CP sin[( CB) ].
56.
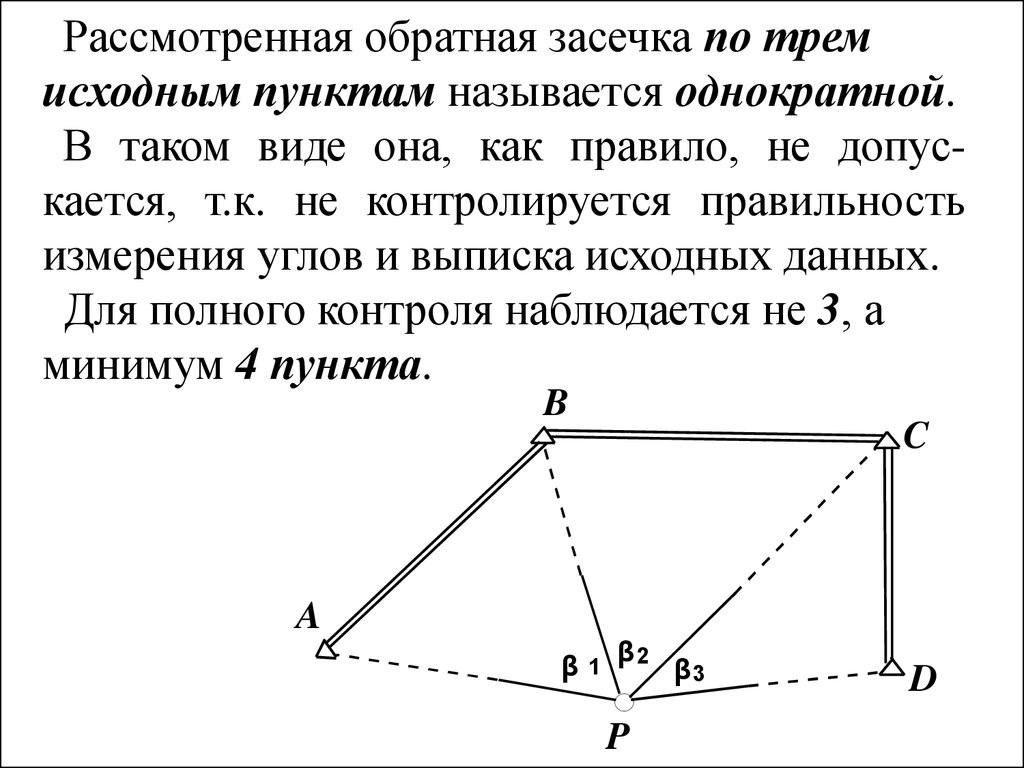
Рассмотренная обратная засечка по тремисходным пунктам называется однократной.
В таком виде она, как правило, не допускается, т.к. не контролируется правильность
измерения углов и выписка исходных данных.
Для полного контроля наблюдается не 3, а
минимум 4 пункта.
B
C
A
β
1
β2
P
β3
D
57.
Задача решается дважды при различномсочетании исходных пунктов. Например,
первый раз используются пункты А, В, С и
второй раз пункты В, С, D.
Для каждого варианта решения
определяется СКО положения пункта М .
Ожидаемое среднее квадратическое
значение Mr расхождения в положении
пункта Р при двух решениях составит
Mr M M2 .
2
1
2
58.
Отсюда допустимое расхождение взначениях вычисленных координат можно
установить по формуле
X ' X " Y ' Y "
2
2
3M r ,
где X/,Y/ – координаты точки из 1-го решения;
X//,Y// – координаты точки из 2-го решения.
За окончательное значение координат пункта Р
берут среднее арифметическое, которое будет
иметь ошибку
Mr
M
.
2
59.
4. Линейная засечка.Задача
линейной
засечки
заключается в определении координат
третьего пункта по координатам двух
исходных пунктов и измеренным
расстояниям от определяемого пункта
до исходных (однократная засечка).
Для
контроля
определения
используются координаты третьего
исходного пункта и расстояния до него
от определяемого.
60.
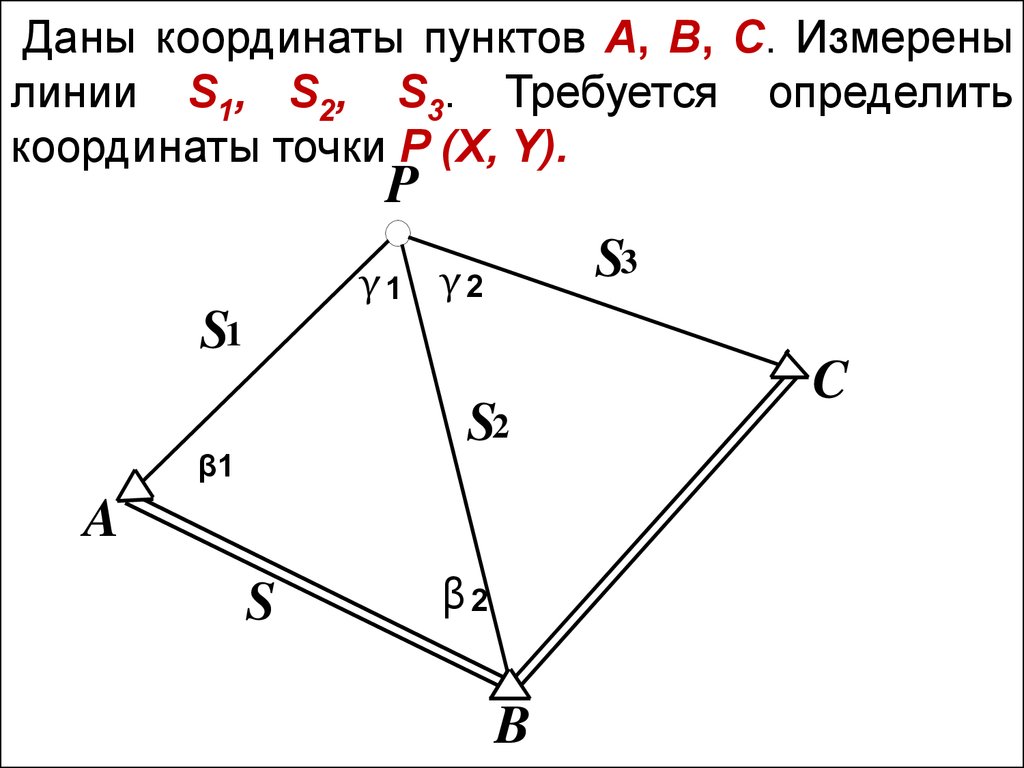
Даны координаты пунктов А, B, C. Измеренылинии S1, S2, S3. Требуется определить
координаты точки P (X, Y).
P
γ1
S3
γ2
S1
S2
β1
A
S
β2
B
C
61.
Рассмотрим однократную засечку сиспользованием пунктов А и В.
1. Решением обратной геодезической
задачи определим дирекционный угол и
длину линии АВ:
YB YA
( AB) arctg
XB XA
YB YA X B X A
2
2
S
( X B X A ) (YB YA ) .
sin( AB) cos( AB)
62.
2. Определим уголтеорему косинусов:
β1,
используя
S S S 2SS1 cos 1 ,
2
2
2
2
1
S S S
1 arccos
2SS1
2
2
1
2
2
3. Определим дирекционный угол линии
АР
( AP) ( AB) 1.
63.
4. Определим координаты точки Р:X P X A S1 cos( AP),
YP YA S1 sin( AP).
Для
контроля
решения
вычисляется
длина
линии
сравнивается с измеренной
задачи
ВР
и
BP ( X P X B ) (YP YB ) .
2
2
64.
Расхождение не должно превышать 3-хединиц последнего знака в измеренном
значении линии S2.
Для полного контроля определения
вычисляется
сторона
СР
и
сравнивается с измеренной S3
CP ( X P X C ) (YP YC ) .
2
2
65.
Допускается|СР–S3| <6ms
где ms – СКО измерения расстояний S3.
Однако в целях повышения точности
окончательных
значений
искомых
координат задачу лучше решать дважды.
При втором решении используют
исходные пункты В, С и расстояния S2, S3.
66.
Допустимое расхождение в координатахопределяют по формуле
r
X ' X " Y ' Y "
2
2
3M r .
В свою очередь
Mr M M2 .
2
1
2
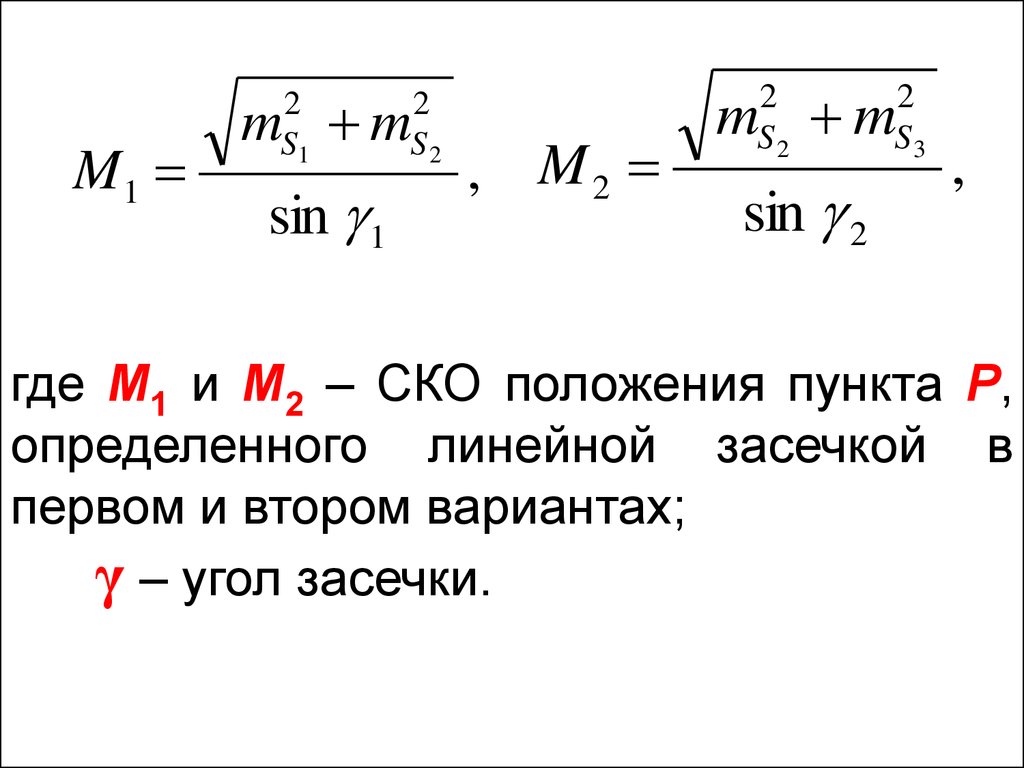
67.
M1m m
2
S1
sin 1
2
S2
, M2
m m
2
S2
sin 2
2
S3
,
где М1 и М2 – СКО положения пункта Р,
определенного линейной засечкой в
первом и втором вариантах;
γ – угол засечки.
68.
Величину угла засечки (для первогорешения) можно найти из выражения
S sin 1
1 arcsin
S2
За окончательное значение координат
пункта Р берут среднее арифметическое,
которое будет иметь ошибку
Mr
M
.
2



























































 geography
geography Construction
Construction








