Similar presentations:
Геодезические сети. Лекция №4
1. Лекция №4
ГЕОДЕЗИЧЕСКИЕ СЕТИ2. Геодезическая сеть -
Геодезическая сеть совокупность точек, закрепленныхна земной поверхности, положение
которых определено в общей для
них системе координат и высот.
Различают:
- Плановые сети
(х, у или B,L);
- Высотные сети (Н);
- Пространственные сети
(X, Y, Z или B, L, H)
3.
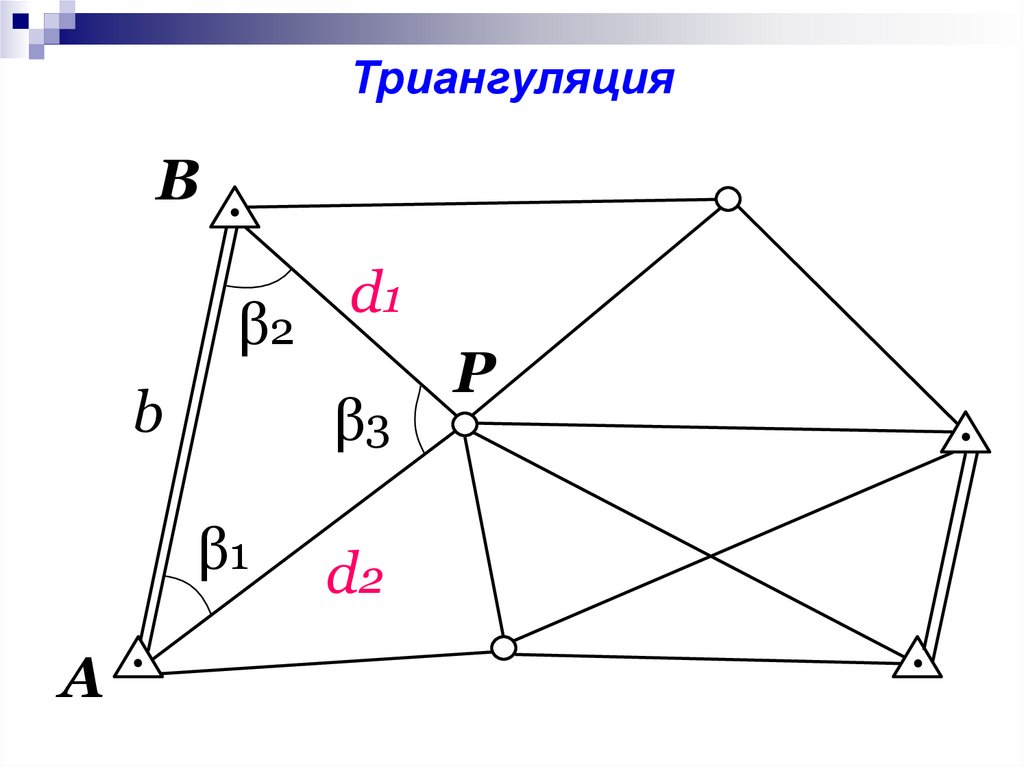
Методы построения плановых сетейТриангуляция
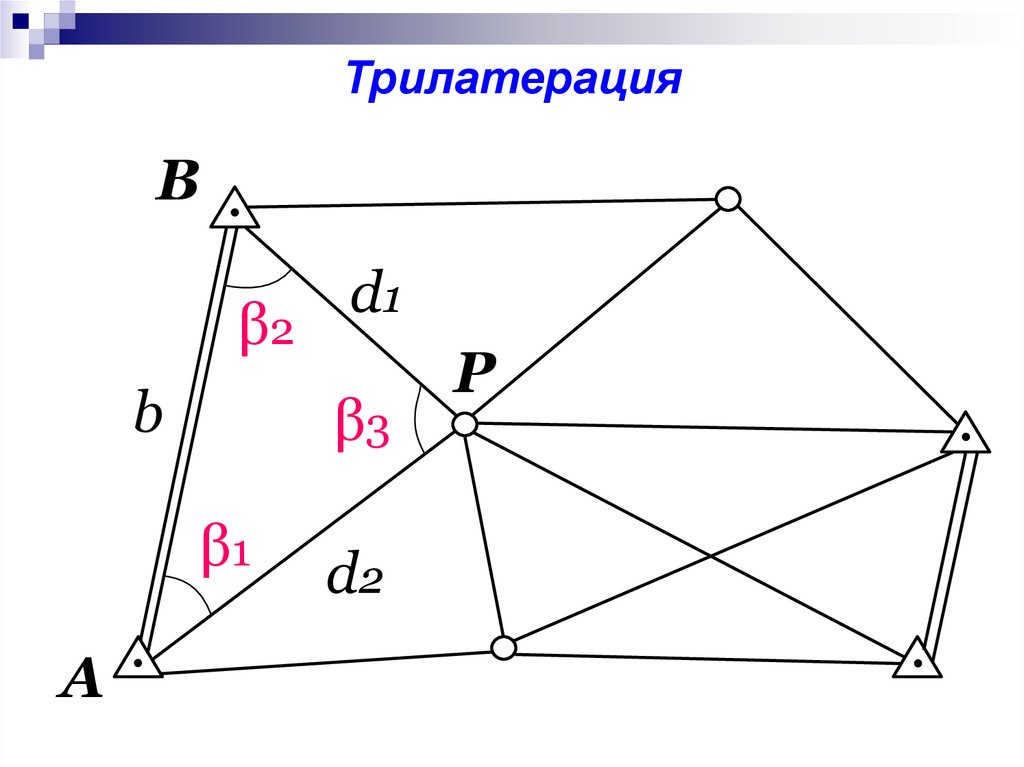
Трилатерация
Линейно-угловая
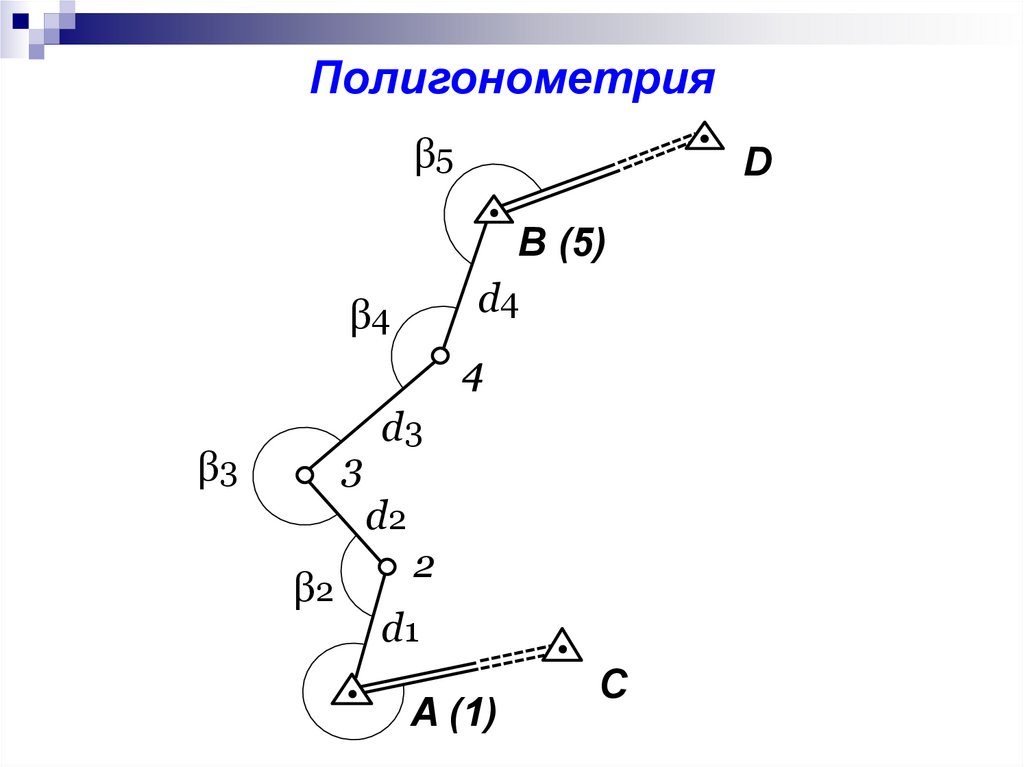
Полигонометрия
Спутниковый метод
4.
ТриангуляцияB
β2
b
β3
β1
A
d1
d2
P
5.
ТрилатерацияB
β2
b
β3
β1
A
d1
d2
P
6.
Полигонометрияβ5
D
B (5)
d4
β4
4
β3
3
d3
d2
β2
2
d1
A (1)
С
7.
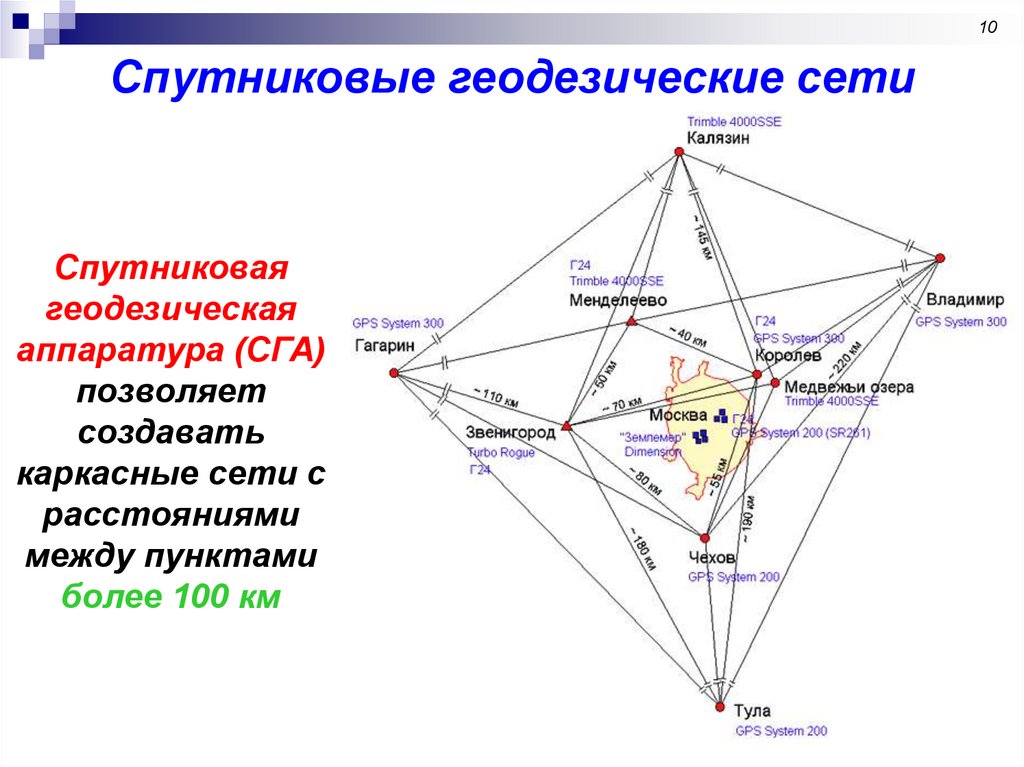
10Спутниковые геодезические сети
Спутниковая
геодезическая
аппаратура (СГА)
позволяет
создавать
каркасные сети с
расстояниями
между пунктами
более 100 км
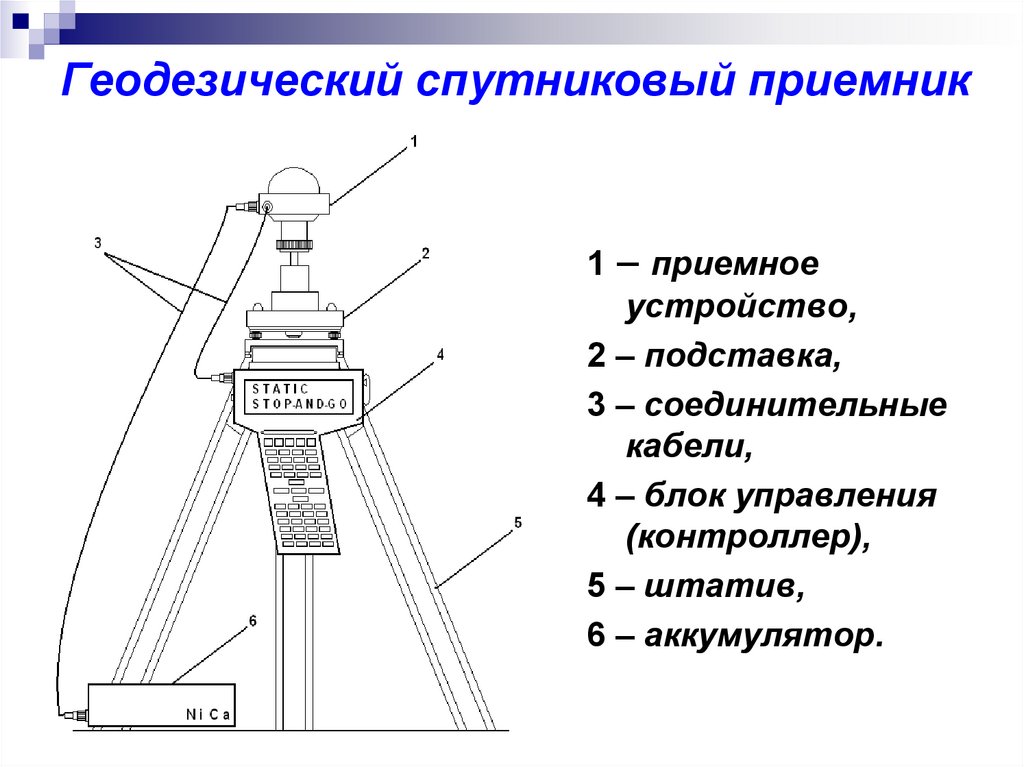
8. Геодезический спутниковый приемник
1 – приемноеустройство,
2 – подставка,
3 – соединительные
кабели,
4 – блок управления
(контроллер),
5 – штатив,
6 – аккумулятор.
9. GPS-приемники
10.
Классификация плановых геодезическихсетей
Государственная геодезическая сеть:
ФАГС;
ВГС;
СГС-1.
Сети сгущения
Геодезические сети специального
назначения
Съемочные сети
11.
Сеть пунктов ФАГС и ВГС на 2003г.Анадырь
Певек
Билибино
Марково
ОСЛО
КОПЕНГАГЕН
Мурманск
Чокурдах
Алакуртти
СТОКГОЛЬМ
Среднеколымск
БЕРЛИН
Октябрьский
Калевала
ХЕЛЬСИНКИ
Тикси
ТАЛЛИН
Эвенск
Кемь
Калининград
Лахколамен
Светлое
РИГА
Сеймчан
Сегозеро
Саскылах
Кресты
Пулково
ВАРШАВА
Архангельск
Псков
Нарьян-Мар
Амдерма
Хатанга
Мезень
ВИЛЬНЮС
Новгород
Батагай
Усть-Нера
Плесецк
Пикалево
Бологое
МИНСК
Верх. Тойма
Нелидово
Весьегонск
Харовск
Сыня
Тверь
Унеча
Менделеево
Хандыга
Салехард
Усть-Большерецк
Охотск
Сыктывкар
Чухлома
Войвож
ЦНИИГАиК
Нов. Уренгой
Кинешма
Владимир
Ветлуга
Тула
Орел
Петропавловск-Камчатский
Норильск
Котлас
Ярославль
МОСКВА
Давыдово
КИЕВ
Жиганск
Оленёк
Венденга
Смоленск
Пущино
Магадан
Воркута
Вел. Луки
Гагарин
Верх. Кривого
Транспортный
Вытегра
Якутск
Мураши
Туруханск
Вилюйск
Рязань
Муром
КИШЕНЕВ
Курск
Коренево
Ниж. Новгород
Тура
Елец
Воронеж
Пильна
Тамбов
Каменск-Шахтинский
Ейск
Чернышевский
Пенза
Ульяновск
Сызрань
Екатеринбург
Ванавара
Нерюнгри
Бодайбо
Тюмень
Экимчан
Ильинский
Колпашево
Челябинск
Александров Гай
Чкаловский
Смирных
Полины Осипенко
Нижнешадрино
Тобольск
Уфа
Зимовники
Ставрополь
Чумикан
Байкит
Красноуфимск
Самара
Абдулино
Ноглики
Алдан
Нижневартовск
Волгоград
Новопокровская
Туапсе
Ханты-Мансийск
Междуреченск
Набережные Челны
Саратов
Петров Вал
Ершов
Краснодар
Оха
Николаевск-на-Амуре
Олёкминск
Пермь
Тамань
Анапа
Аян
Мирный
Казань
Агрыз
Поворино
Михайловка
Ростов-на-Дону
Тутончаны
Ноябрьск
Серов
Ртищево
Казанская
Советский
Яр
Верхнеимбатск
Саранск
Ровенки
Юксеево
Яранск
Сасово
Белгород
Верх. Баскунчак
Новая Чара
Енисейск
Курган
Голышманово
Зея
Сов. Гавань
Бол. Невер
Спицино
Усть-Кут
Ургал 1
Карталы
Буденовск
Астрахань
Пятигорск
Южно-Сахалинск
Оренбург
Элиста
Зеленчук
Орск
Северное
Мариинск
Красноярск
Могоча
Братск
Тайшет
Свободный
Хабаровск
Багдарин
Северобайкальск
Омск
Максимовка
Известковый
Новосибирск
Артезиан
Качуг
Зима
Усть-Баргузин
Пожарское
Карасук
Чита
ТБИЛИСИ
Новокузнецк
Абакан
Иркутск
Веселый Яр
Борзя
ЕРЕВАН
Бийск
Монды
Турий Рог
Улан-Удэ
Кызыл
Киевка
Кыра
Кызыл-Мажалык
БАКУ
Владивосток
Усть - Кокса
Краскино
УЛАН-БАТОР
ТОКИО
12.
Классификация плановых геодезическихсетей
Государственная геодезическая сеть:
ФАГС;
ВГС;
СГС-1.
Сети сгущения
Геодезические сети специального
назначения
Съемочные сети
13.
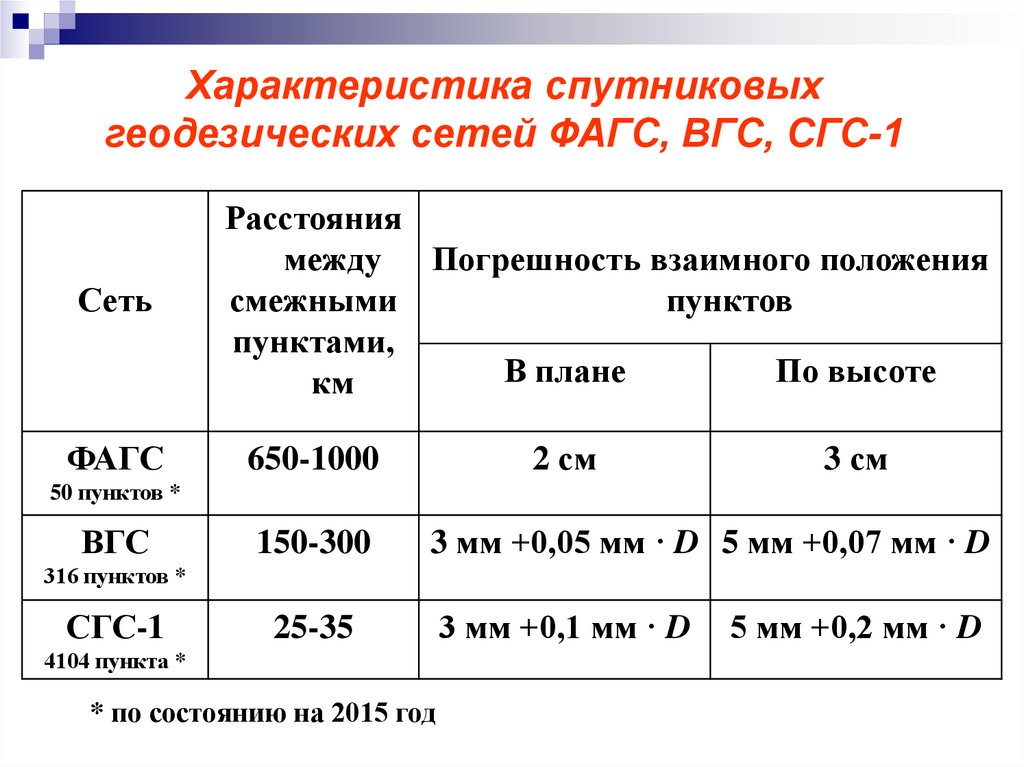
Характеристика спутниковыхгеодезических сетей ФАГС, ВГС, СГС-1
Сеть
ФАГС
Расстояния
между Погрешность взаимного положения
смежными
пунктов
пунктами,
В плане
По высоте
км
2 см
650-1000
3 см
50 пунктов *
ВГС
150-300
3 мм +0,05 мм · D 5 мм +0,07 мм · D
316 пунктов *
СГС-1
25-35
4104 пункта *
* по состоянию на 2015 год
3 мм +0,1 мм · D
5 мм +0,2 мм · D
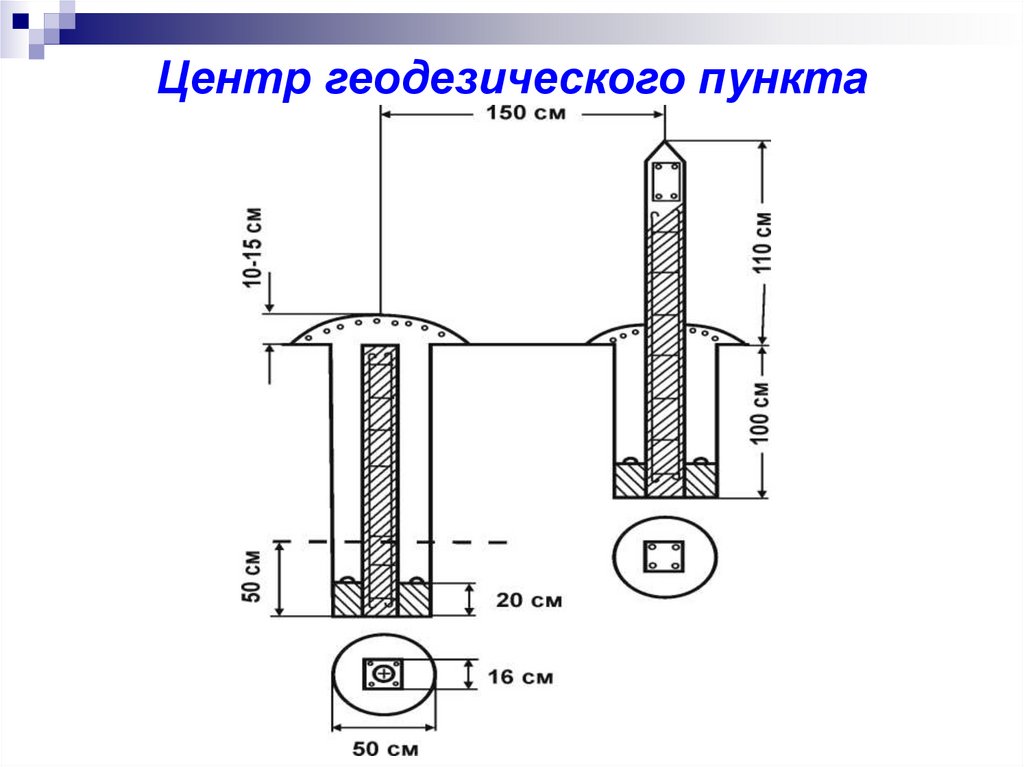
14. ЗАКРЕПЛЕНИЕ ПУНКТОВ ГЕОДЕЗИЧЕСКИХ СЕТЕЙ
15.
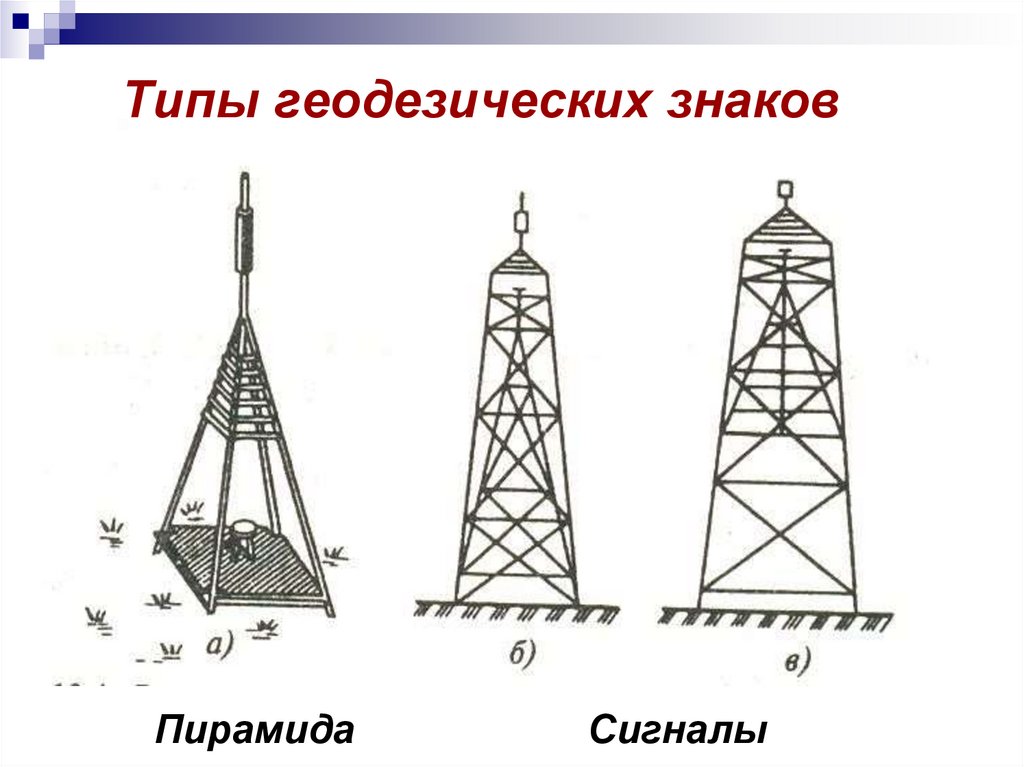
Центр геодезического пункта16. Типы геодезических знаков
ПирамидаСигналы
17. Пункт геодезической разбивочной сети на строительстве КАД
18. Пункт съёмочной сети
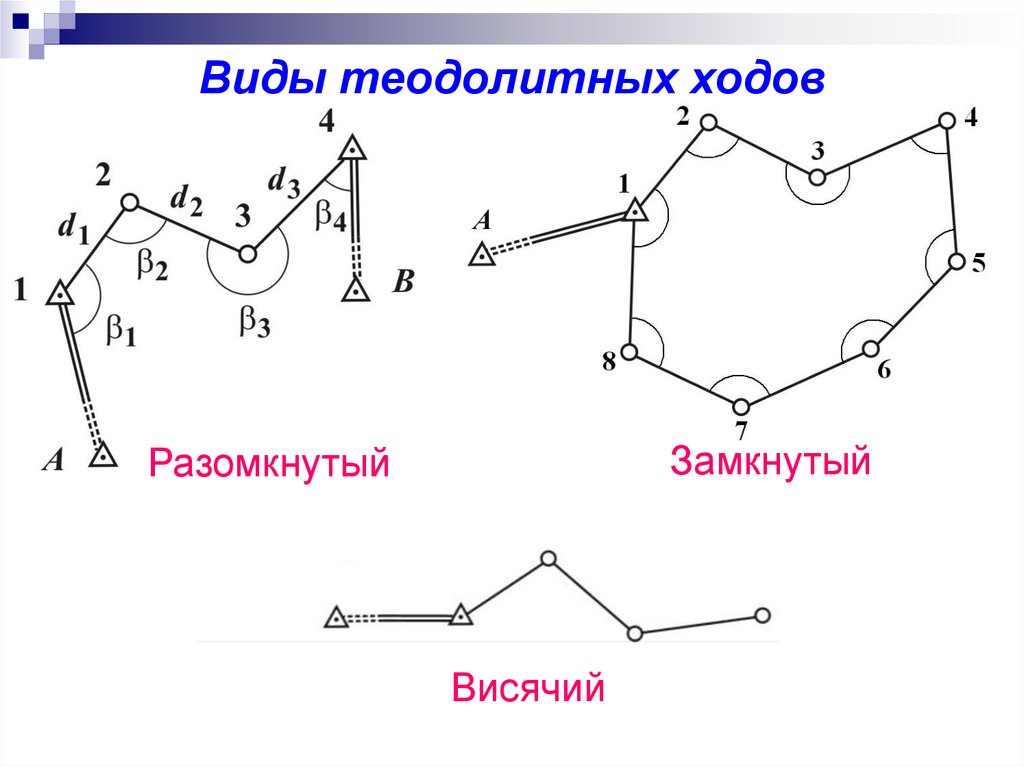
19. ТЕОДОЛИТНЫЙ ХОД
20. ТЕОДОЛИТНЫЙ ХОД
-ход полигонометрии пониженной
точности.
Применяется, в основном, для
создания съемочных сетей.
21.
Виды теодолитных ходовЗамкнутый
Разомкнутый
Висячий
22. Последовательность работ при прокладке теодолитного хода
1.2.
3.
4.
Проектирование хода на
топографической карте или плане.
Рекогносцировка и закрепление точек
хода на местности.
Измерение углов поворота и длин
сторон в ходе.
Обработка теодолитного хода
(вычисления в ведомости координат).
23.
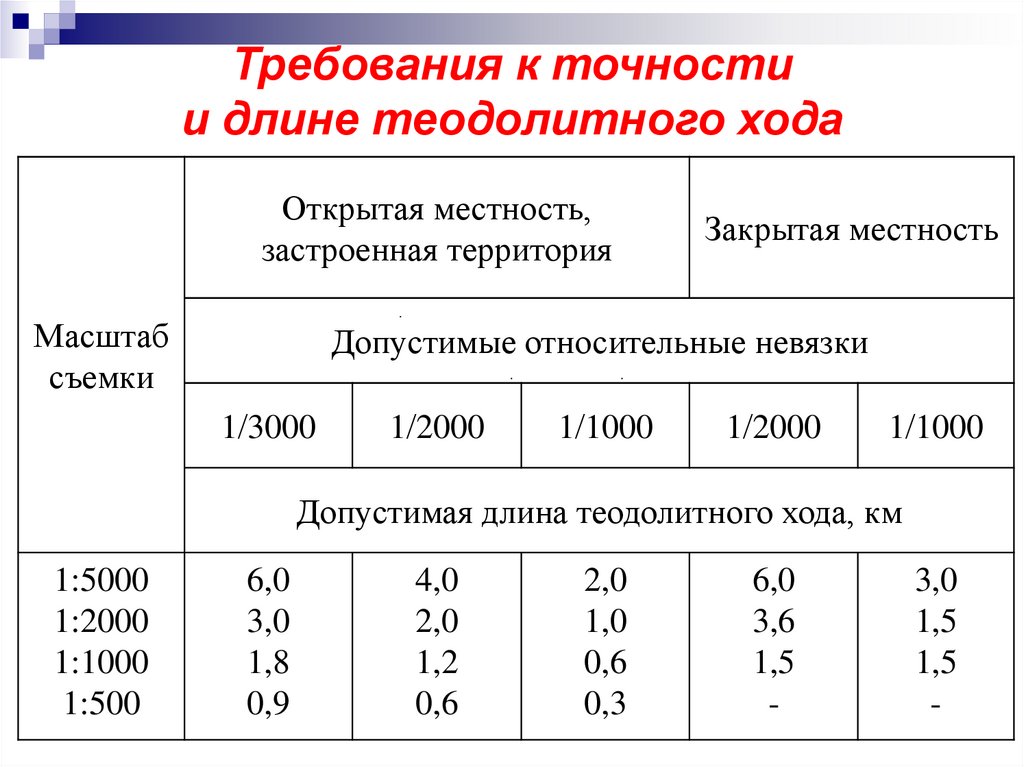
Требования к точностии длине теодолитного хода
Открытая местность,
застроенная территория
Масштаб
съемки
Закрытая местность
Допустимые относительные невязки
1 3000
1 2000
1 1000
1 2000
1 1000
Допустимая длина теодолитного хода, км
1:5000
1:2000
1:1000
1:500
6,0
3,0
1,8
0,9
4,0
2,0
1,2
0,6
2,0
1,0
0,6
0,3
6,0
3,6
1,5
-
3,0
1,5
1,5
-
24.
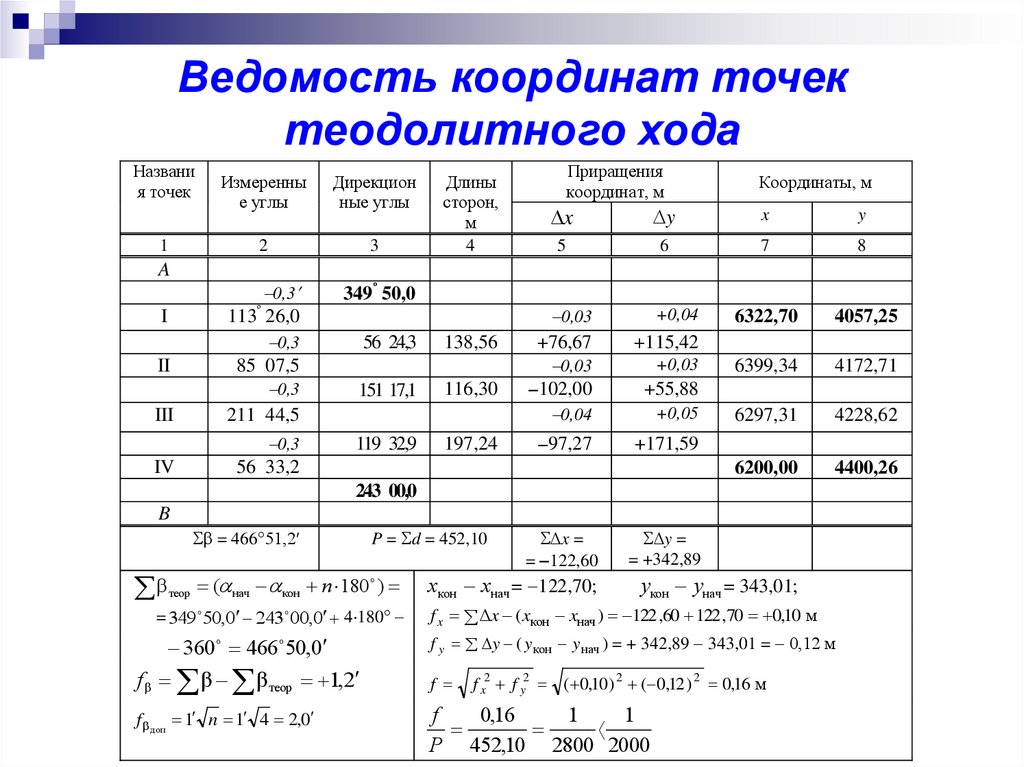
Ведомость координат точектеодолитного хода
Названи
я точек
1
Измеренны
е углы
Дирекцион
ные углы
2
3
A
0,3
I
II
III
113º 26,0
0,3
85 07,5
0,3
211 44,5
0,3
IV
Длины
сторон,
м
4
349º 50,0
56 24,3
151 17,1
119 32,9
138,56
116,30
197,24
Приращения
координат, м
Координаты, м
x
y
x
y
5
6
7
8
6322,70
4057,25
6399,34
4172,71
6297,31
4228,62
6200,00
4400,26
0,03
+0,04
+76,67
0,03
102,00
0,04
+115,42
97,27
+171,59
+0,03
+55,88
+0,05
56 33,2
243 00,0
B
= 466 51,2′
β
теор
P = d = 452,10
( нач кон n 180 )
= 349 50,0 243 00,0 4 180
360 466 50,0
f β β β теор 1,2
f доп 1 n 1 4 2,0
x =
= 122,60
xкон xнач = 122,70;
y =
= +342,89
yкон yнач = 343,01;
f x x ( xкон xнач ) 122 ,60 122 ,70 0,10 м
f y y ( y кон y нач ) = + 342,89 343,01 = 0,12 м
f
f x2 f y2 ( 0,10 ) 2 ( 0,12 ) 2 0,16 м
f
0,16
1
1
P 452,10 2800 2000
25. Обработка замкнутого теодолитного хода
Угловая невязка:f изм. 180 (n 2)
f д о п. 1
Линейные невязки:
f x xi
f y yi
f абс.
f отн.
f x2 f y2
f абс.
1
P
2000
n
26. ЗАСЕЧКИ
27.
aб
Р
Р
в
D
С
β3
β1
β2
Р
β1
А
β2
С
B
А
B
Р
г
д
d1
А
С
B
Р
d3
d2
А
B
С
А
B
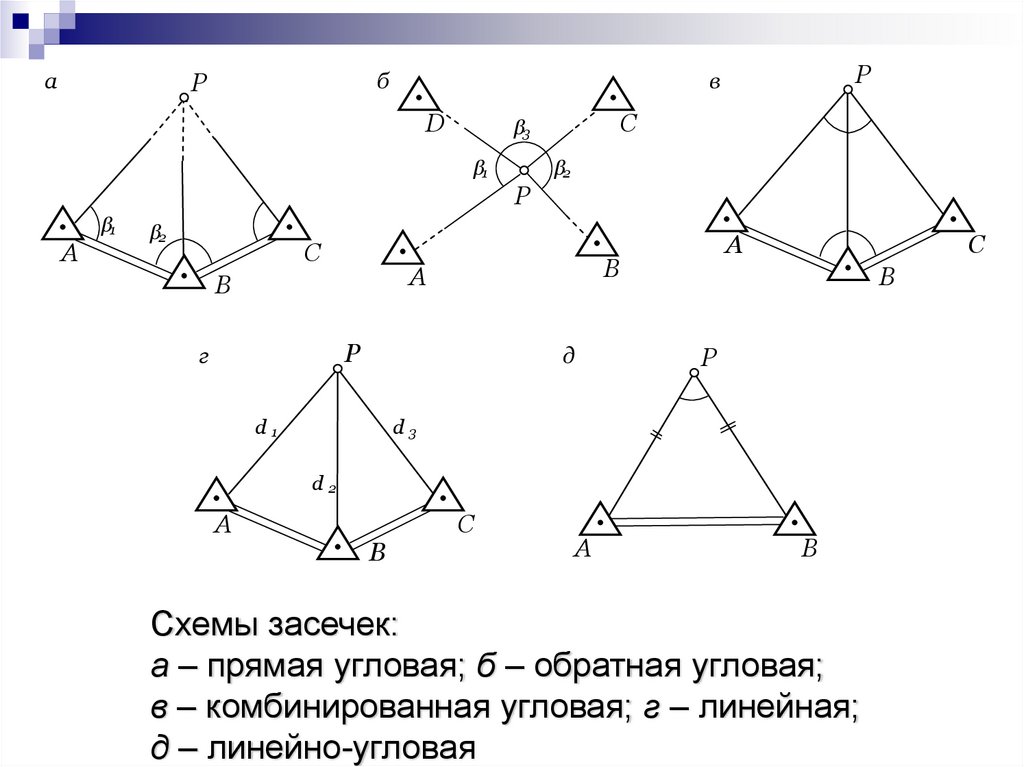
Схемы засечек:
а – прямая угловая; б – обратная угловая;
в – комбинированная угловая; г – линейная;
д – линейно-угловая
28.
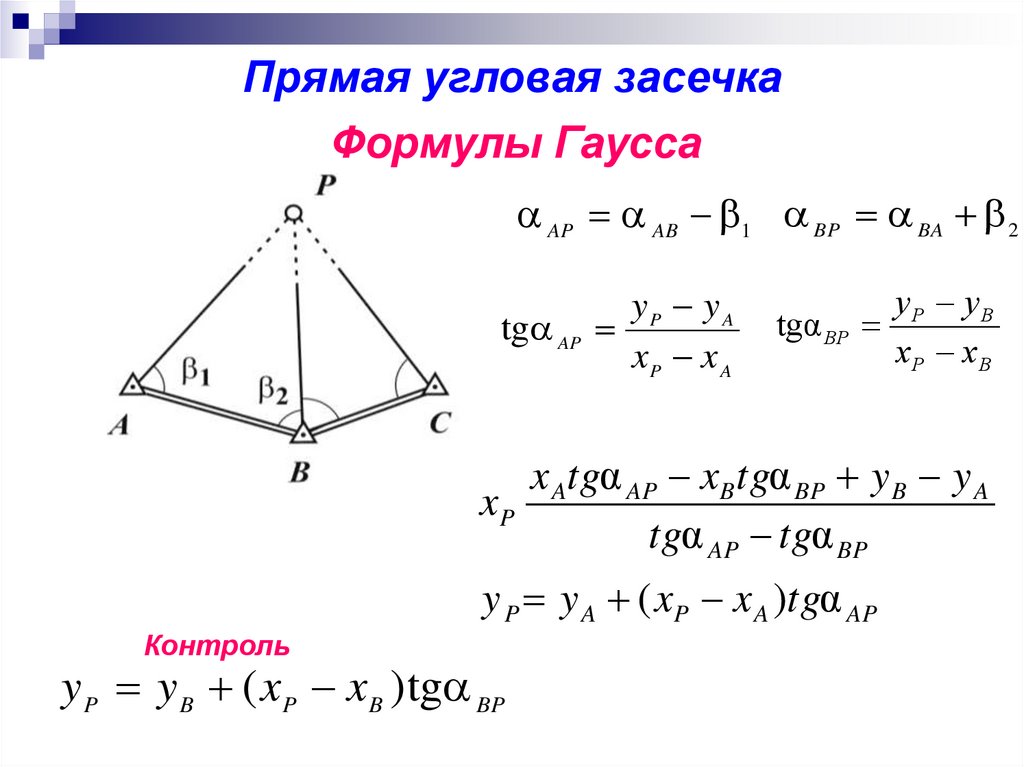
Прямая угловая засечкаФормулы Гаусса
AP AB 1 BP BA 2
tg AP
yP y A
xP x A
tgα BP
yP yB
xP xB
x Atgα AP xB tgα BP y B y A
xP
tgα AP tgα BP
y P y A ( xP x A )tgα AP
Контроль
y P y B ( x P x B ) tg BP
29.
Прямая угловая засечкаФормулы Юнга
x Actg 2 xB ctg 1 y B y A
xP
ctg 1 ctg 2
y Actg 2 y B ctg 1 x A xB
yP
ctg 1 ctg 2
30.
Обратная угловая засечкаtgα BP
y Actgβ1 yB (ctgβ1 ctgβ 2 ) yC ctgβ 2 xA xC
xActgβ1 xB (ctgβ1 ctgβ 2 ) xC ctgβ 2 y A yC
AP BP 1

















 mathematics
mathematics geography
geography








