Подібні трикутники

1.

T
K
P
E
D
H
Черкаська приватна загальноосвітня
школа “Софія”
вчитель математики
Ратушна Аліна Валеріївна

2.

Усім нам часто доводиться мати справу з предметами
однакової форми, але різних розмірів.
Наприклад: зменшена модель автомобіля схожа на
справжній автомобіль. Але їх розміри відповідно
пропорційні.

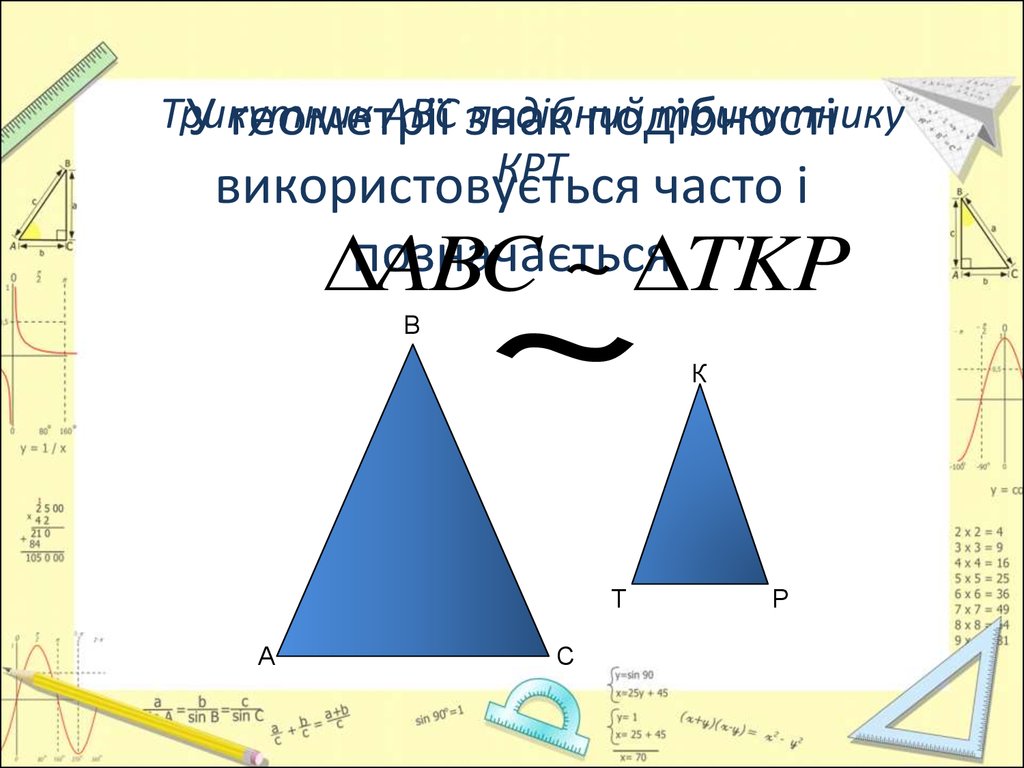
3. У геометрії знак подібності використовується часто і позначається

Трикутник
АВС знак
подібний
трикутнику
У геометрії
подібності
КРТ
використовується
часто і
позначається
ABC ~ TKP
В
~
Т
А
С
К
Р

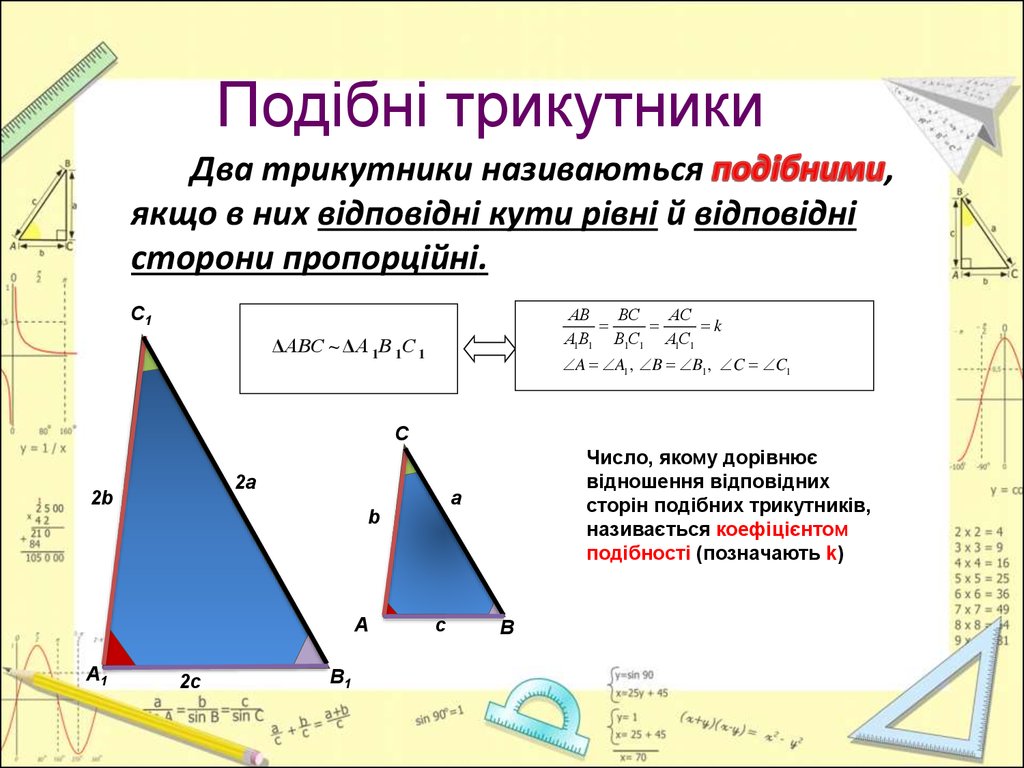
4. Подібні трикутники

Два трикутники називаються
,
якщо в них відповідні кути рівні й відповідні
сторони пропорційні.
С1
АВ
ВC
АС
k
А1 В1 В1С1 А1С1
ΔАВС ~ ΔА 1В 1С 1
A A1 , B B1 , C C1
C
2a
2b
Число, якому дорівнює
відношення відповідних
сторін подібних трикутників,
називається коефіцієнтом
подібності (позначають k)
a
b
А
А1
2c
В1
c
В

5.

Відношення периметрів подібних
трикутників дорівнює відношенню
їх відповідних сторін.
С
АВ ВC
АС P
k
А1 В1 В1С1 А1С1 P1
Щоб скласти відношення відповідних сторін
подібних трикутників, потрібно:
визначити відповідно рівні кути трикутника;
з'ясувати, які сторони є відповідними;
записати рівність трьох дробів, у чисельниках
яких – сторони одного з трикутників, а у
знаменниках – відповідні сторони іншого
А
В
АВ
ВC
АС
P
k
А1 В1 В1С1 А1С1 P1
А1
В1

6.

ФАЛЕС МІЛЕТСЬКИЙ
(кін. 624 – кін. 546 до н. е.)
«Блаженство тіла – в здоров’ї,
блаженство розуму – в знаннях»

7.

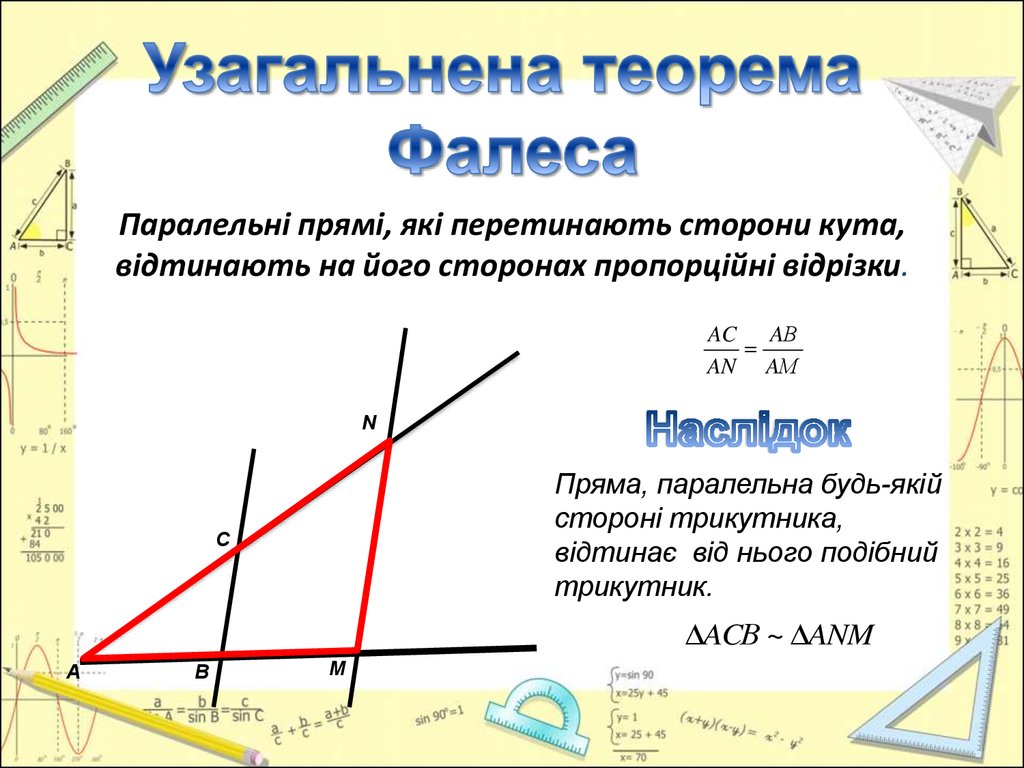
Паралельні прямі, які перетинають сторони кута,
відтинають на його сторонах пропорційні відрізки.
AC AВ
AN AМ
N
Пряма, паралельна будь-якій
стороні трикутника,
відтинає від нього подібний
трикутник.
С
ACВ ~ ANM
А
В
М

8.

довести рівність кутів даних
трикутників;
довести пропорційність відповідних
сторін даних трикутників.
С
А
В
А1
В1

9.

Теорема
(ознака подібності трикутників за двома кутами).
Якщо два кути одного трикутника
відповідно дорівнюють двом
кутам другого трикутника, то
такі трикутники – подібні.
ABC ~ A1B1C1
А
В
А1
В1

10.

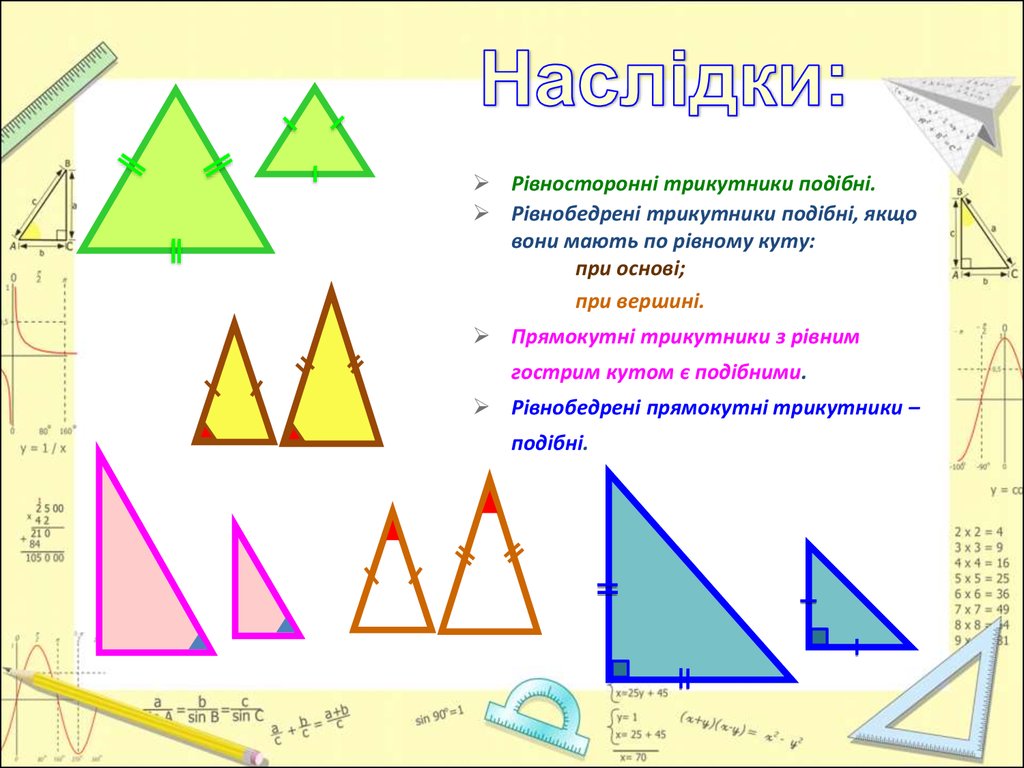
Рівносторонні трикутники подібні.
Рівнобедрені трикутники подібні, якщо
вони мають по рівному куту:
при основі;
при вершині.
Прямокутні трикутники з рівним
гострим кутом є подібними.
Рівнобедрені прямокутні трикутники –
подібні.

11.

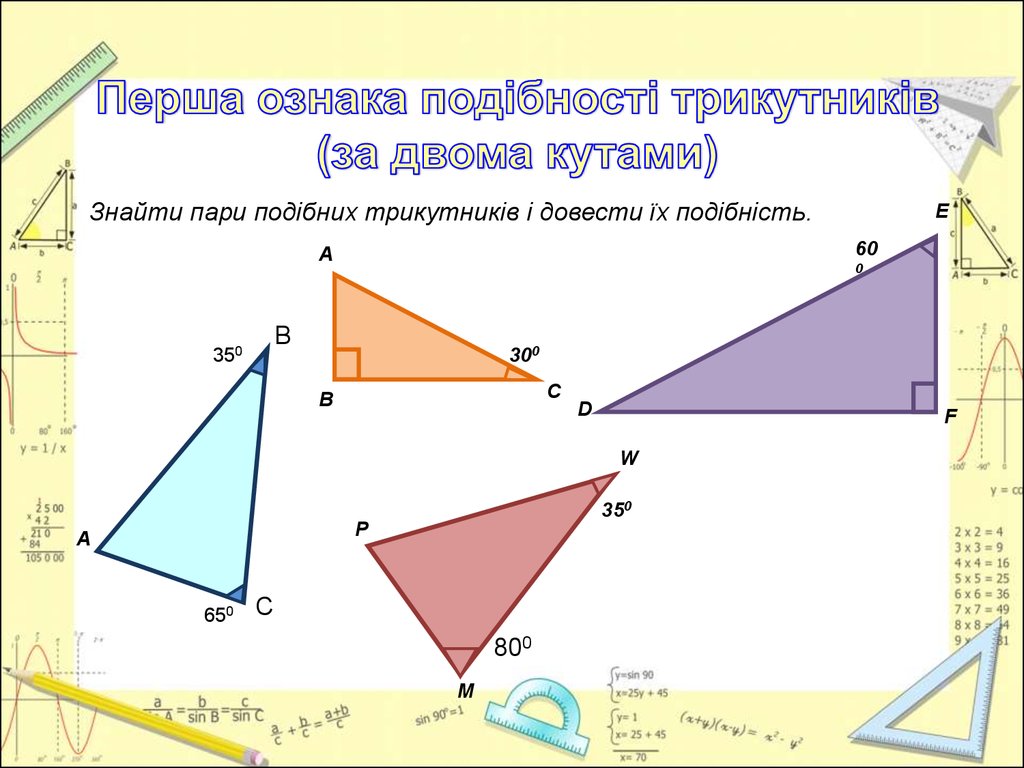
Знайти пари подібних трикутників і довести їх подібність.
60
А
0
В
350
300
С
В
D
F
W
350
Р
А
650
E
С
800
М

12.

Знайти пари подібних трикутників і довести їх подібність.
В
В
300
B1
300
400
N
A1
А
1100
С
А
С
C1
М
Р

13.

Знайти пари подібних трикутників і довести їх подібність. Записати
рівність відношень відповідних сторін.
С
K
ABC ~ MNC
AC DC AB
MC BC MN
М
N
Z
А
PKT ~ ZKX
PT KT PK
ZX KX ZK
В
P
X
T

14.

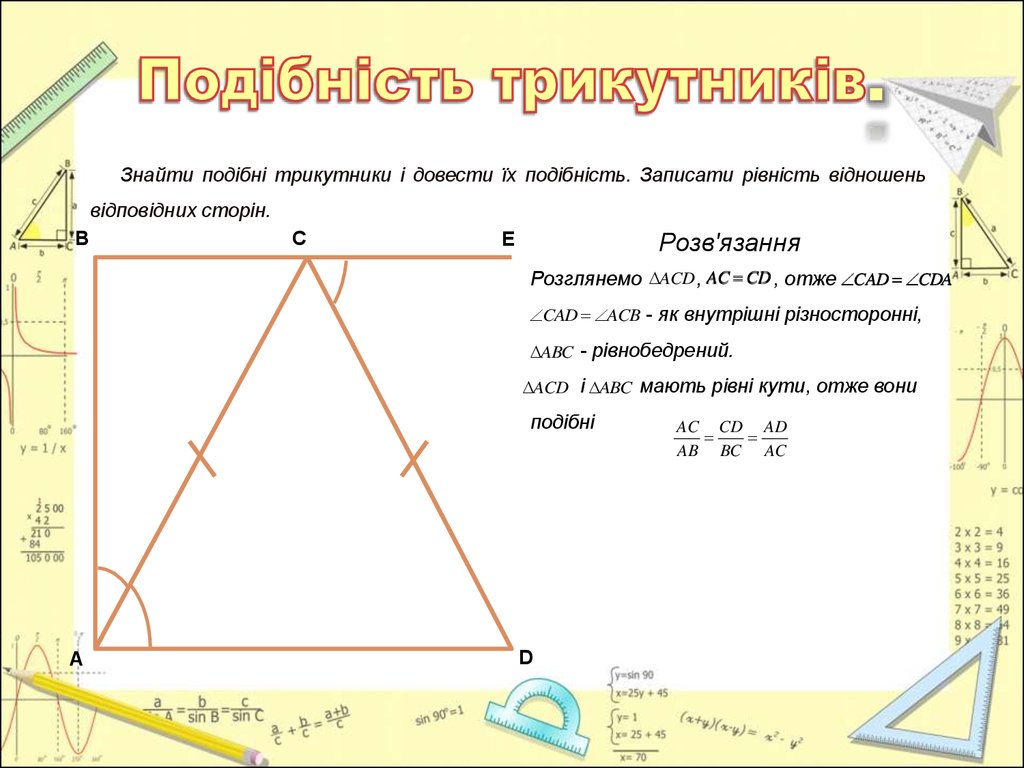
Знайти подібні трикутники і довести їх подібність. Записати рівність відношень
відповідних сторін.
B
C
Розв'язання
E
Розглянемо ACD , AC CD , отже CAD CDA
CAD ACB - як внутрішні різносторонні,
ABC - рівнобедрений.
ACD і ABC мають рівні кути, отже вони
подібні
A
D
AC CD AD
AB BC AC

15.

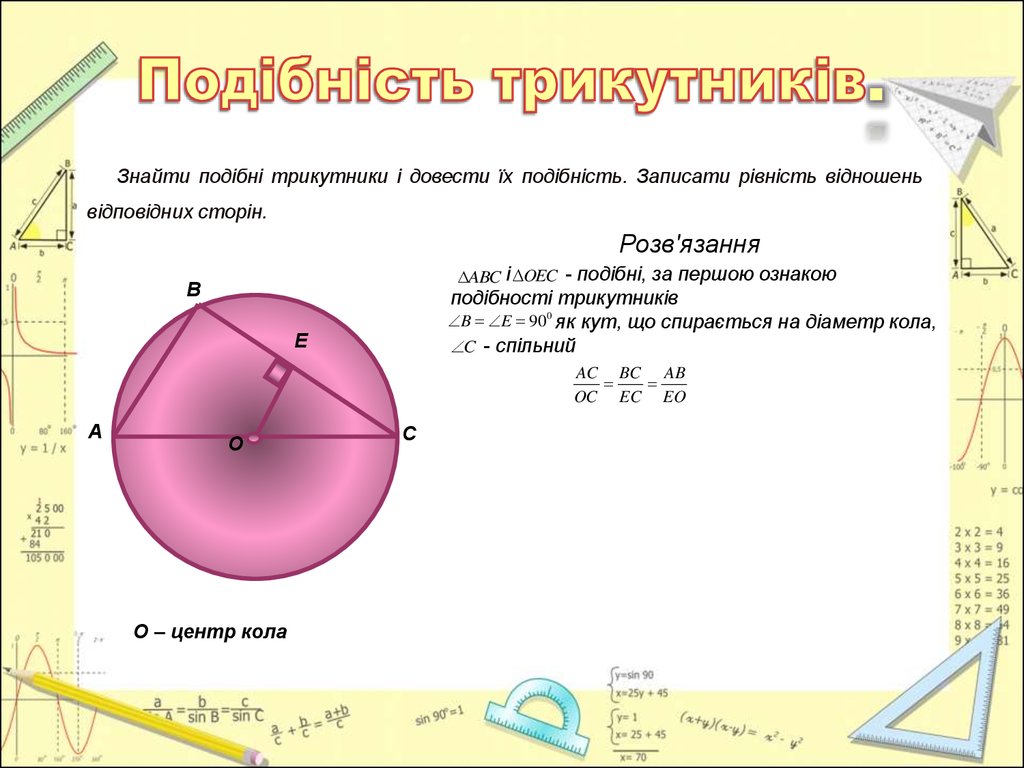
Знайти подібні трикутники і довести їх подібність. Записати рівність відношень
відповідних сторін.
Розв'язання
ABC і OEC - подібні, за першою ознакою
В
подібності трикутників
B E 900 як кут, що спирається на діаметр кола,
C - спільний
Е
AC BC AB
OC EC EO
А
О
O – центр кола
С

16.

Знайти подібні трикутники і довести їх подібність. Записати рівність відношень
відповідних сторін.
Розв'язання
В
ACD ~ OAK за двома кутами.
C 900 - як кут, що спирається на діаметр
С
кола.
К
A 900, тому що AB AD (як дотична до
діаметра)
А
D
О
АВ - дотична
KOA CAD - за умовою
AO AK KO
AC CD AC