Similar presentations:
Компланарные векторы, правило параллелепипеда
1.
2.
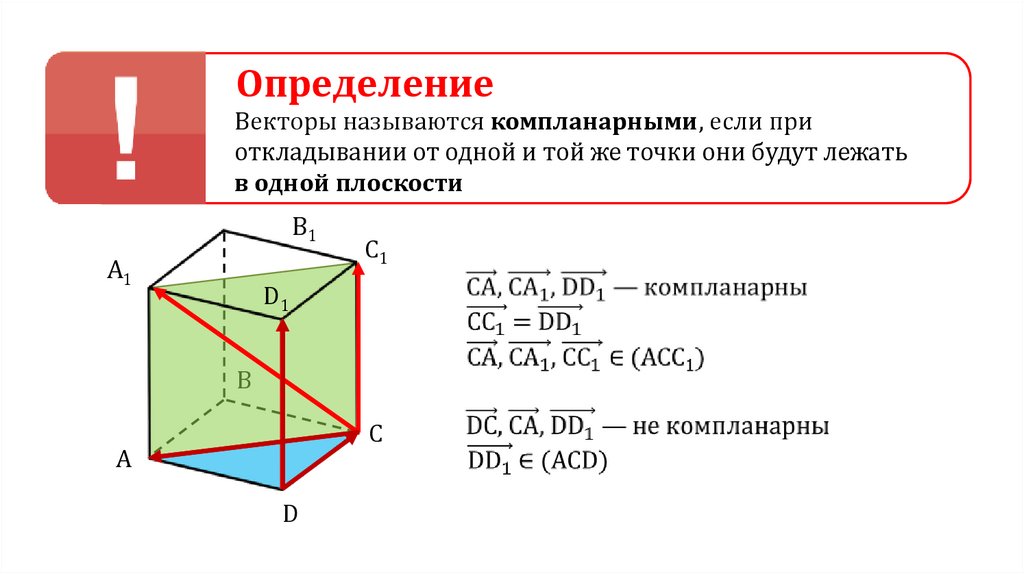
ОпределениеВекторы называются компланарными, если при
откладывании от одной и той же точки они будут лежать
в одной плоскости
B1
A1
C1
D1
B
C
A
D
3.
— Любые два вектора компланарны— Три вектора, среди которых имеются два
коллинеарных, также компланарны
— Три произвольных вектора могут быть как
компланарными, так и некомпланарными
4.
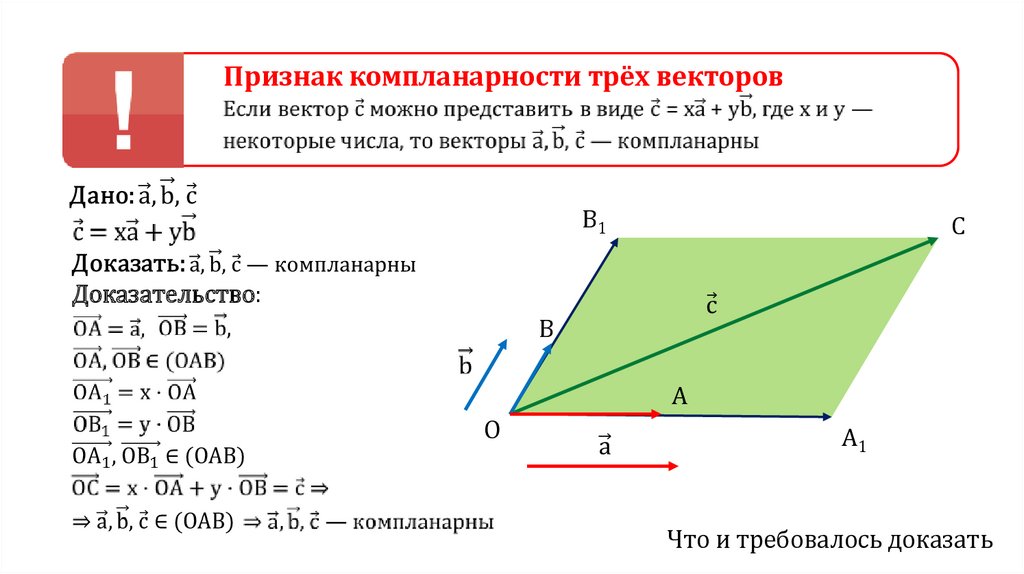
Признак компланарности трёх векторовB1
C
Доказательство:
B
A
O
A1
Что и требовалось доказать
5.
Утверждение, обратное признакукомпланарности векторов:
6.
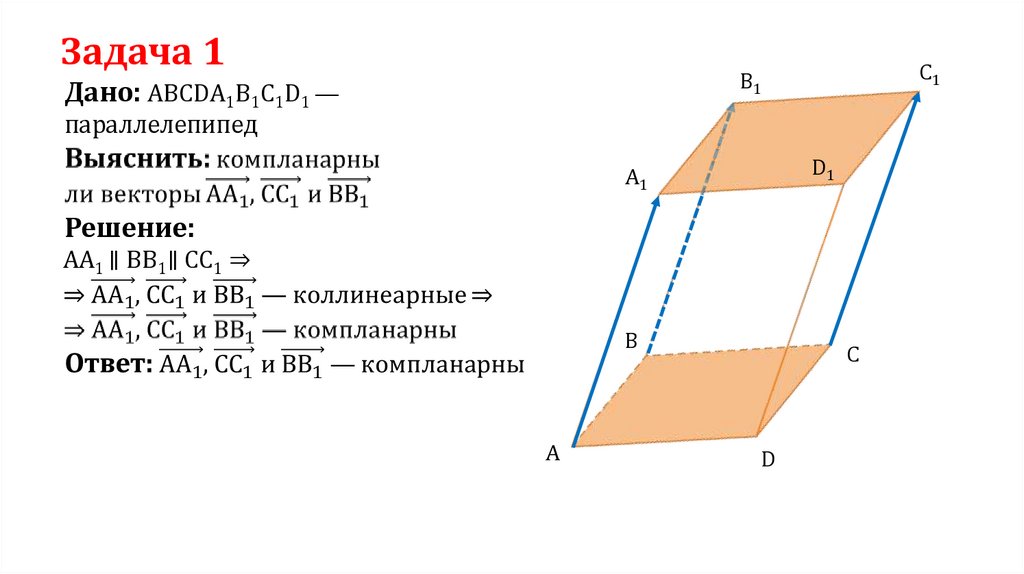
Задача 1C1
B1
Дано: ABCDA1B1C1D1 —
параллелепипед
D1
A1
Решение:
АА1 ∥ BB1∥ CC1 ⇒
B
A
C
D
7.
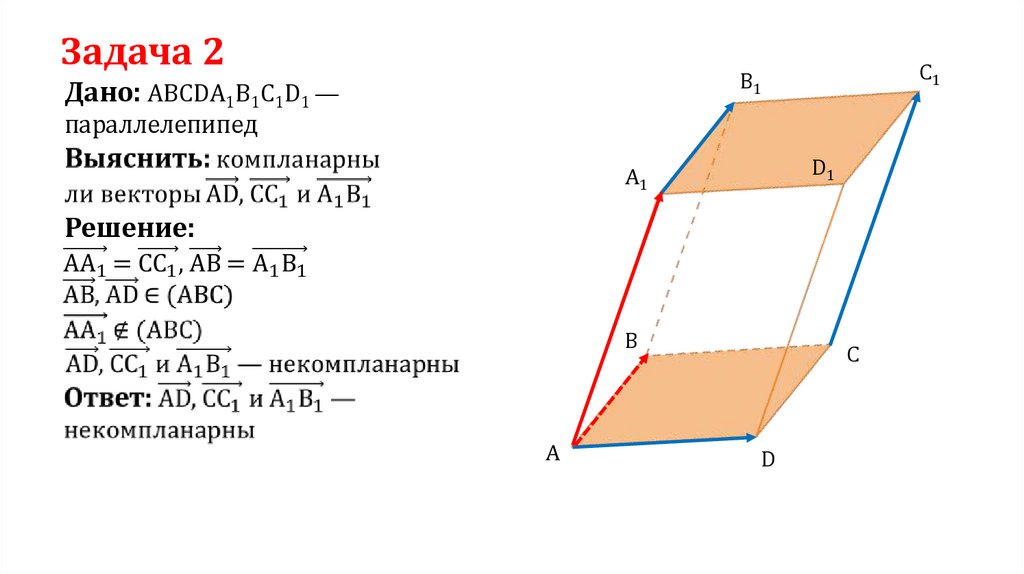
Задача 2C1
B1
Дано: ABCDA1B1C1D1 —
параллелепипед
D1
A1
Решение:
B
A
C
D
8.
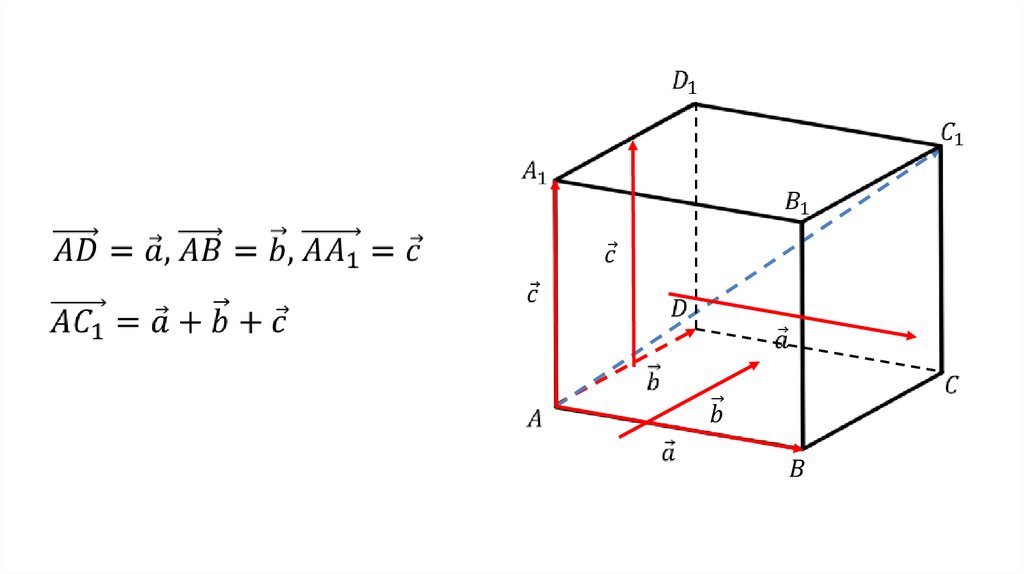
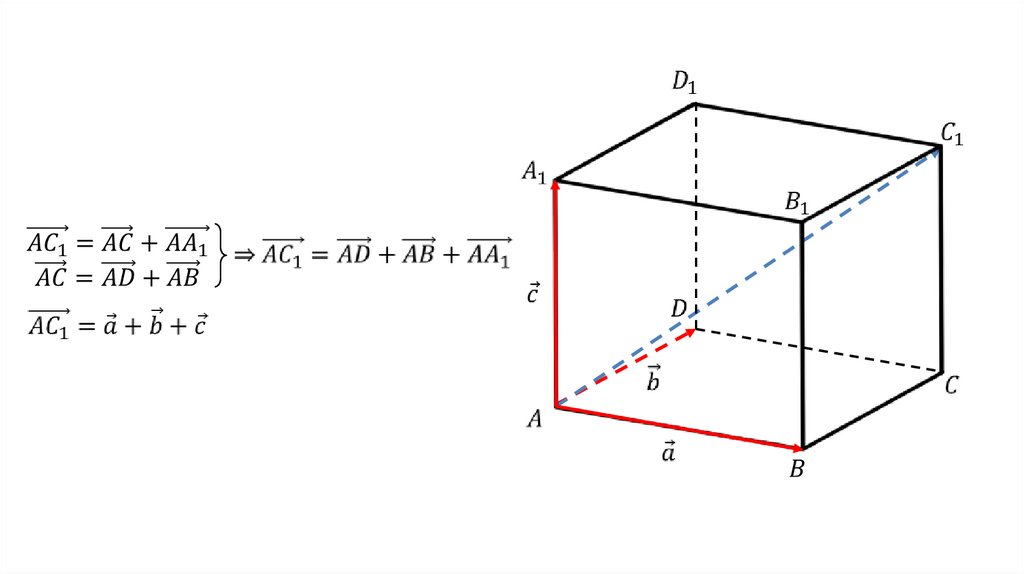
Правило параллелепипедаВектор,
лежащий
на
диагонали
параллелепипеда, равен сумме векторов,
проведенных из той же точки и лежащих на трех
измерениях параллелепипеда.
9.
10.
11.
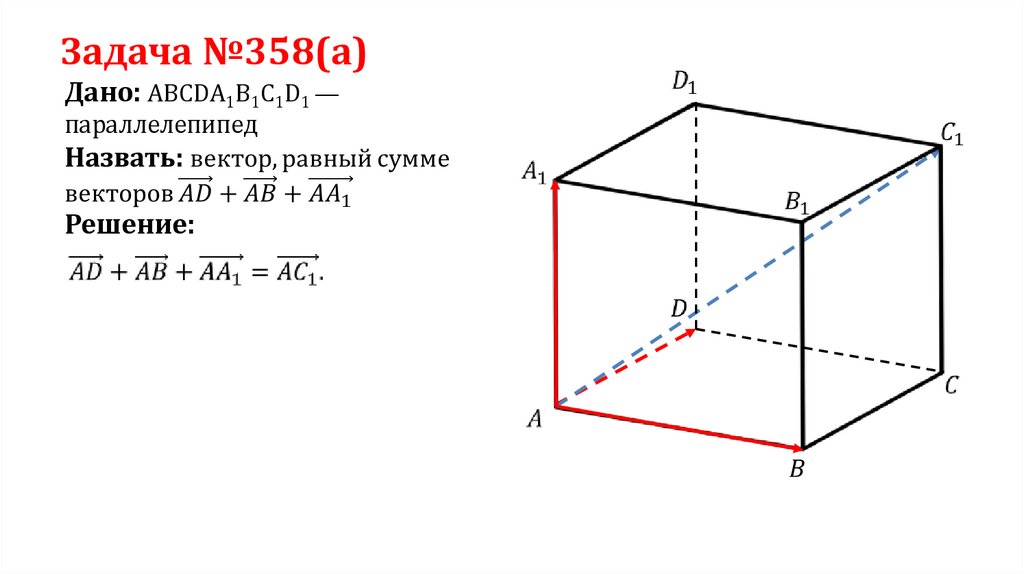
Задача №358(а)Дано: ABCDA1B1C1D1 —
параллелепипед
Решение:
12.
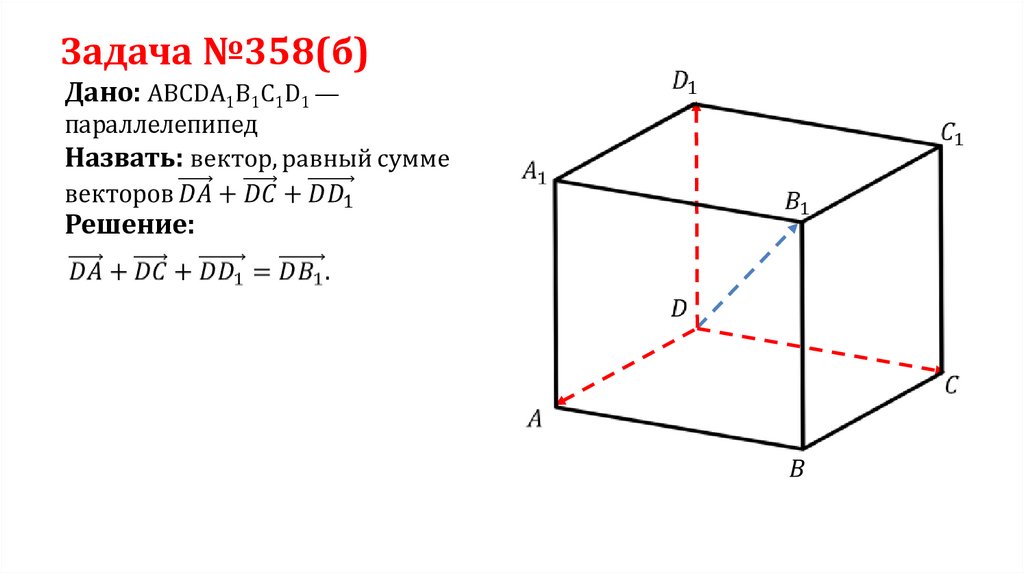
Задача №358(б)Дано: ABCDA1B1C1D1 —
параллелепипед
Решение:
13.
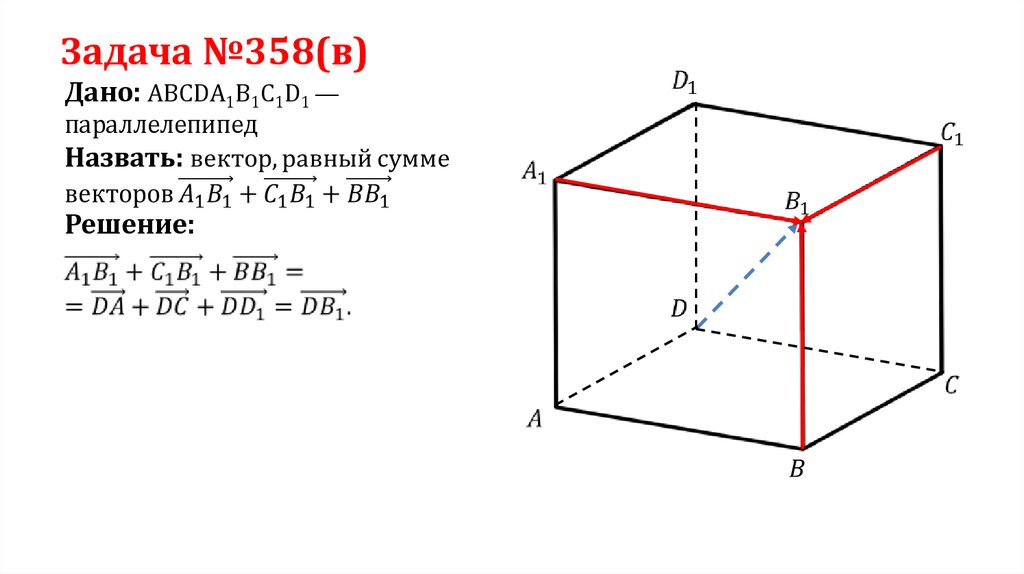
Задача №358(в)Дано: ABCDA1B1C1D1 —
параллелепипед
Решение:
14.
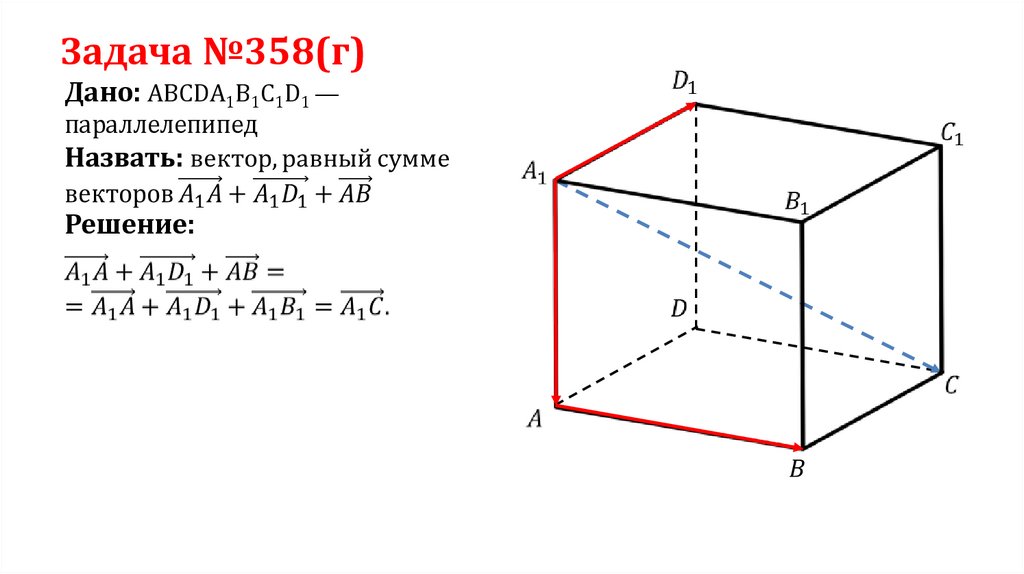
Задача №358(г)Дано: ABCDA1B1C1D1 —
параллелепипед
Решение:
15.
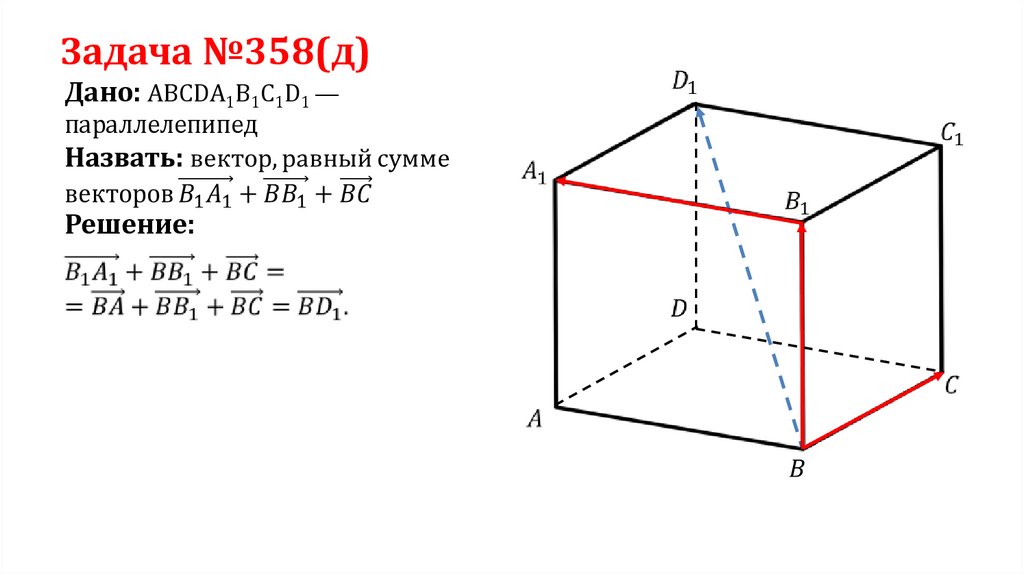
Задача №358(д)Дано: ABCDA1B1C1D1 —
параллелепипед
Решение:
16.
17.
Теорема о разложении векторапо
трём
некомпланарным
векторам
Любой вектор можно разложить по трем
данным некомпланарным векторам, причём
коэффициенты разложения определяются
единственным образом.
18.
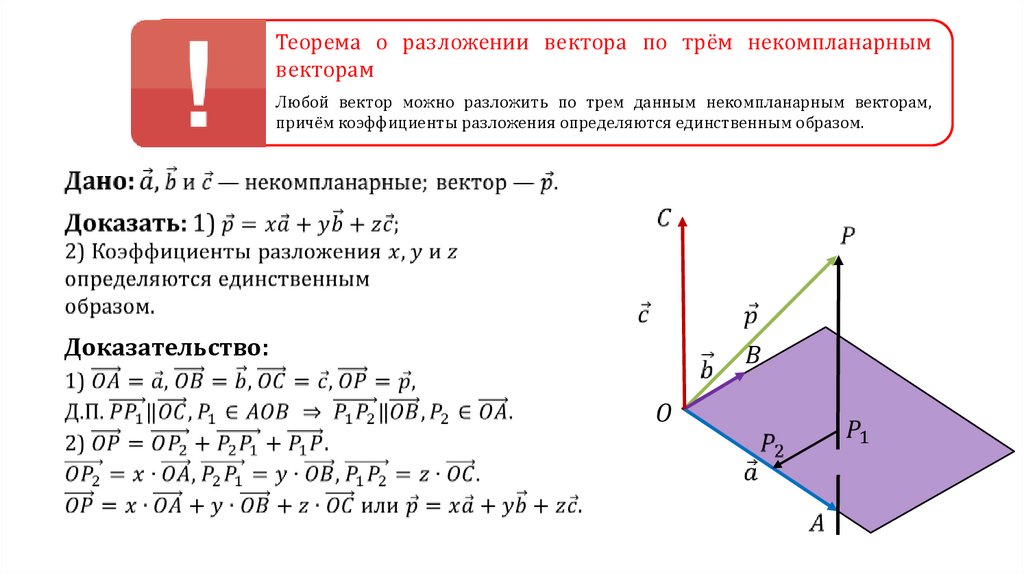
Теорема о разложении вектора по трём некомпланарнымвекторам
Любой вектор можно разложить по трем данным некомпланарным векторам,
причём коэффициенты разложения определяются единственным образом.
Доказательство:
19.
Теорема о разложении вектора по трём некомпланарнымвекторам
Любой вектор можно разложить по трем данным некомпланарным векторам,
причём коэффициенты разложения определяются единственным образом.
Доказательство:
20.
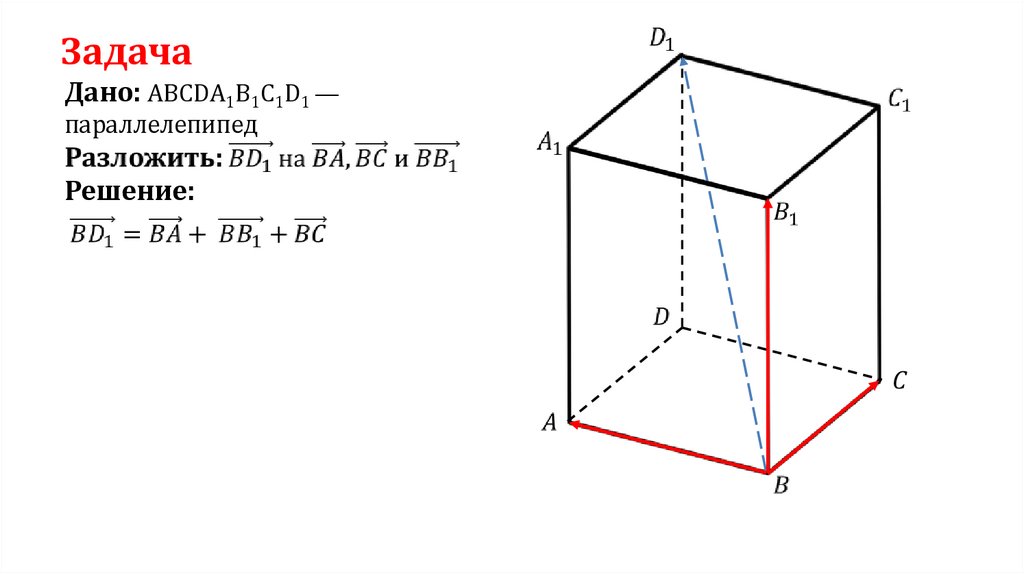
ЗадачаДано: ABCDA1B1C1D1 —
параллелепипед
Решение:
21.
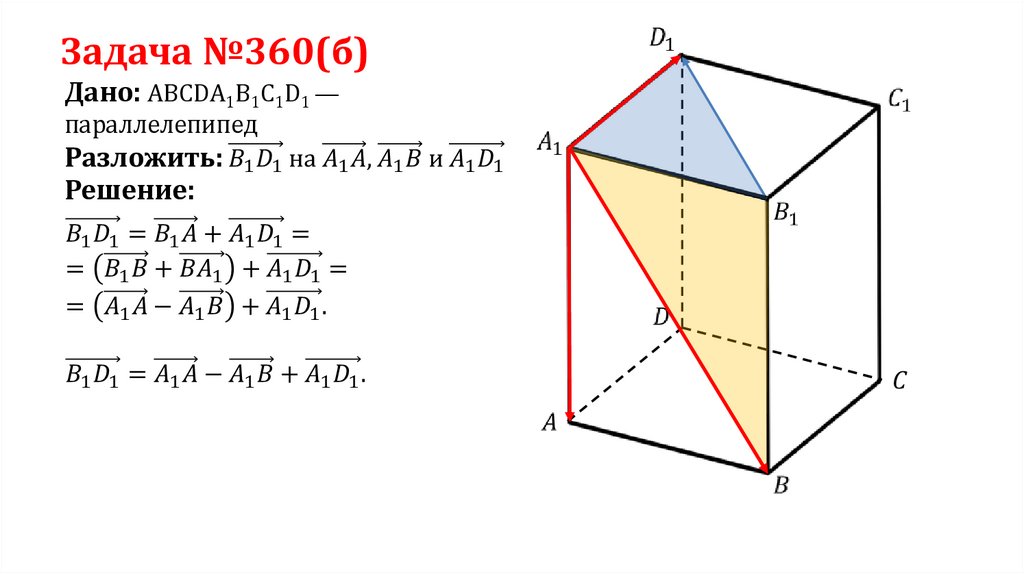
Задача №360(б)Дано: ABCDA1B1C1D1 —
параллелепипед
Решение:







 mathematics
mathematics








