Similar presentations:
Компланарные векторы. (10 класс)
1.
2.
Векторы называются компланарными, если приоткладывании их от одной и той же точки они будут лежать
в одной плоскости.
Другими словами, векторы называются
компланарными, если имеются равные им векторы,
лежащие в одной плоскости.
c
a
Любые два вектора
компланарны.
3.
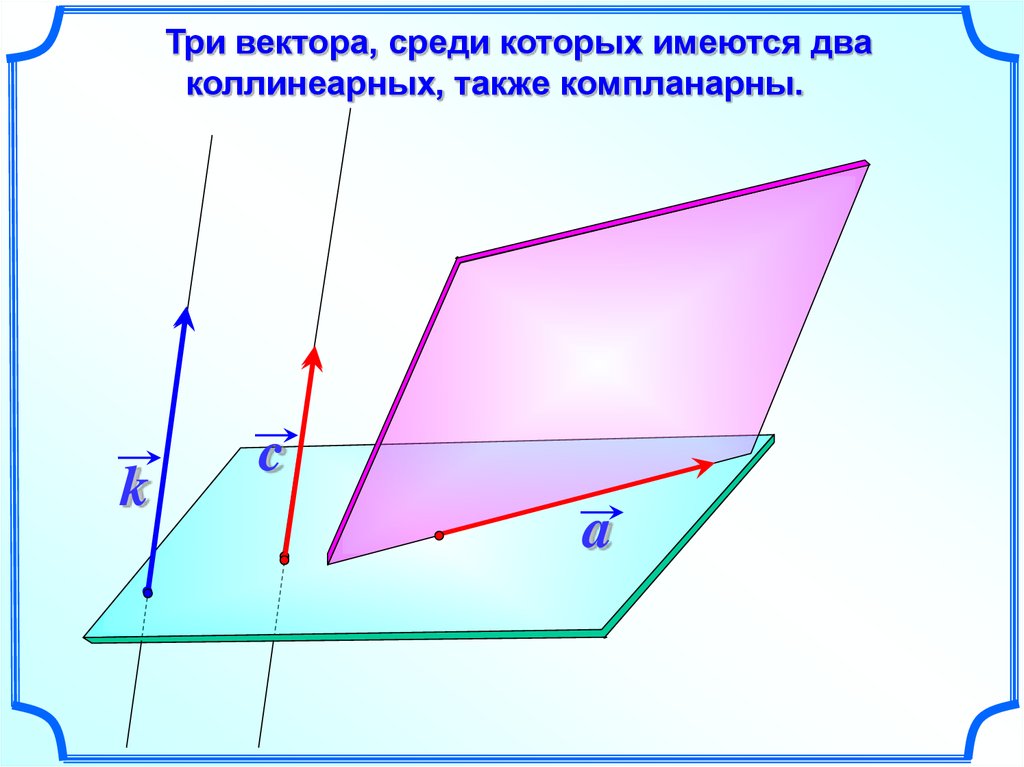
Три вектора, среди которых имеются дваколлинеарных, также компланарны.
k
c
a
4.
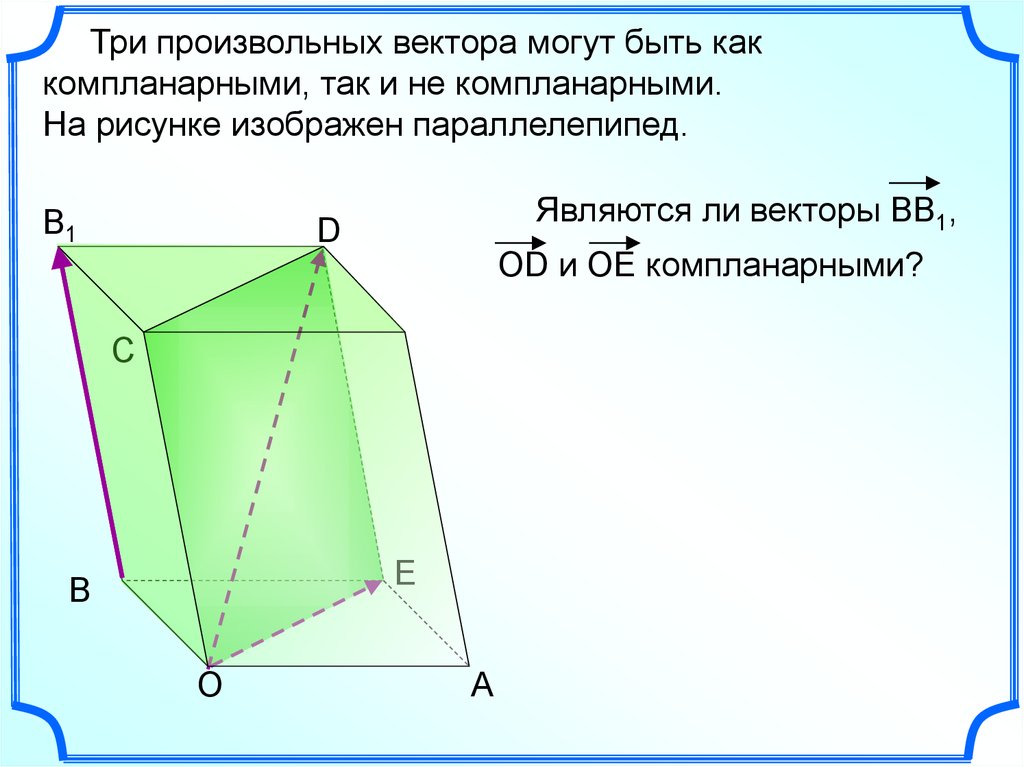
Три произвольных вектора могут быть каккомпланарными, так и не компланарными.
На рисунке изображен параллелепипед.
B1
Являются ли векторы ВВ1,
D
ОD и ОЕ компланарными?
C
Е
В
О
А
5.
Три произвольных вектора могут быть каккомпланарными, так и не компланарными. На рисунке
изображен параллелепипед.
Являются ли векторы ОА,
B1
ОВ и ОС компланарными?
D
C
Векторы ОА, ОВ и ОС не
компланарны, так как вектор
ОС не лежит в плоскости ОАВ.
Е
В
О
А
6.
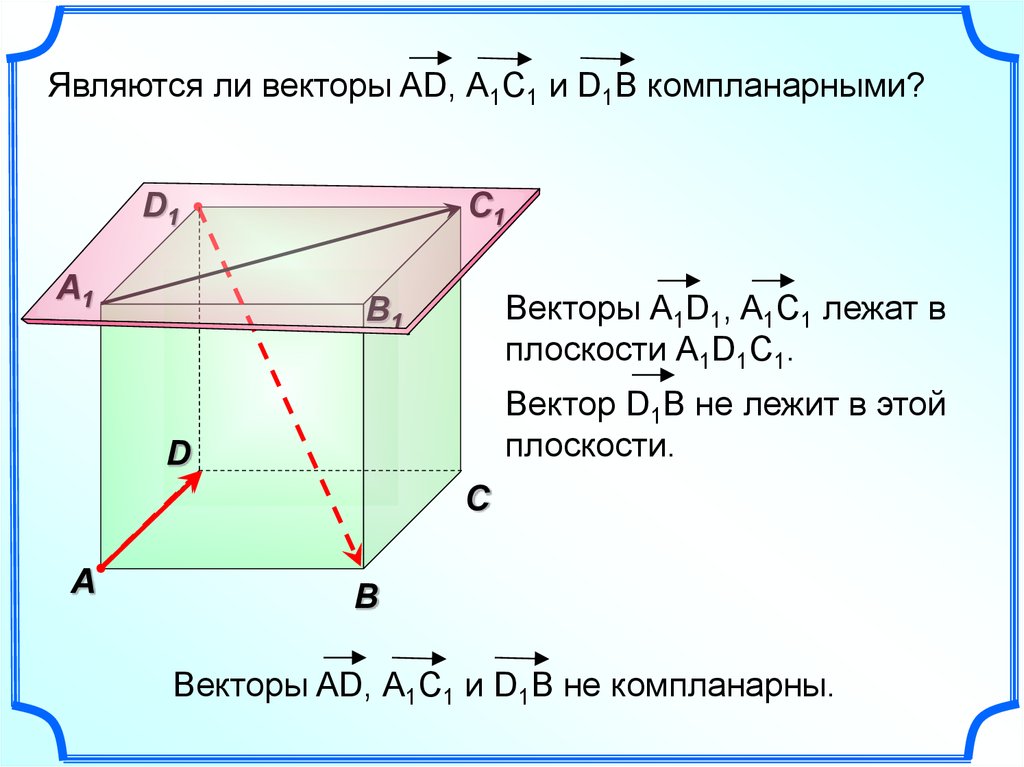
Являются ли векторы AD, А1С1 и D1B компланарными?D1
A1
C1
Векторы А1D1, A1C1 лежат в
плоскости А1D1C1.
B1
Вектор D1В не лежит в этой
плоскости.
D
C
A
B
Векторы AD, А1С1 и D1B не компланарны.
7.
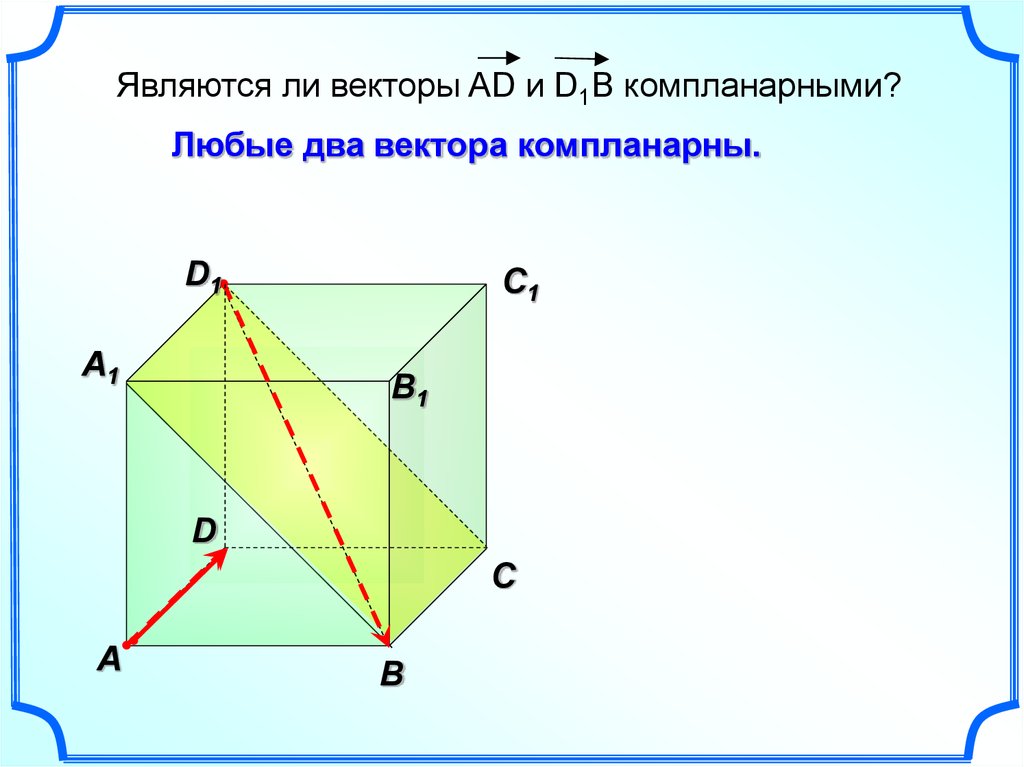
Являются ли векторы AD и D1B компланарными?Любые два вектора компланарны.
D1
A1
C1
B1
D
C
A
B
8.
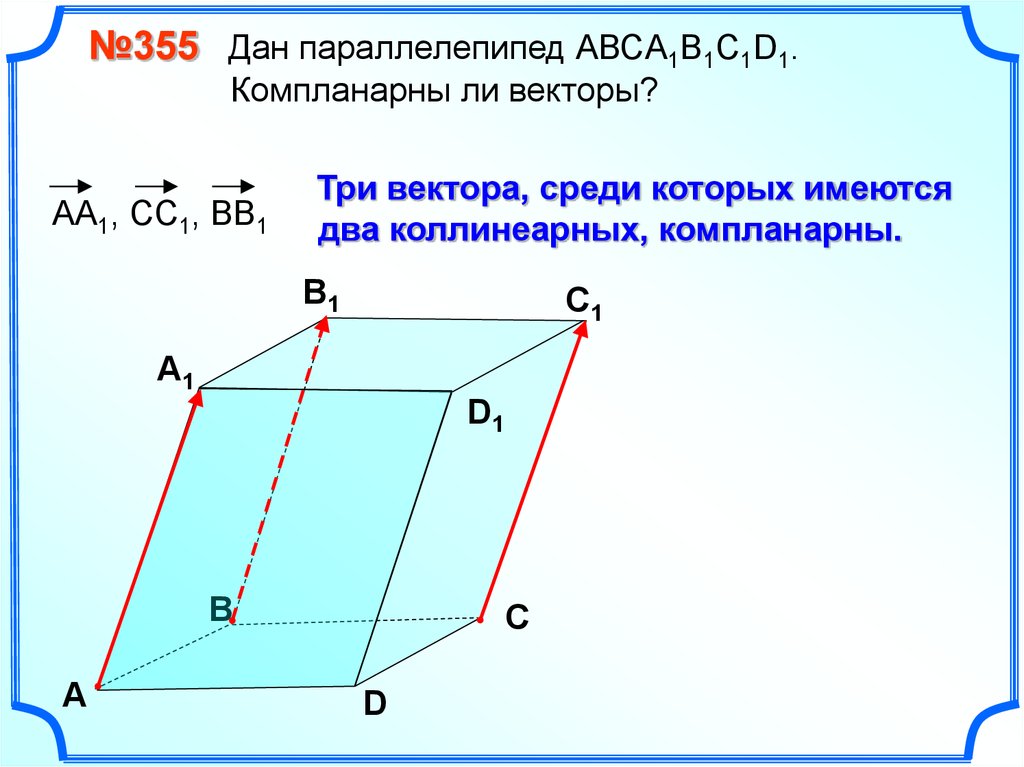
№355 Дан параллелепипед АВСA1B1C1D1.Компланарны ли векторы?
АА1, СС1, ВВ1
Три вектора, среди которых имеются
два коллинеарных, компланарны.
В1
С1
А1
D1
В
А
С
D
9.
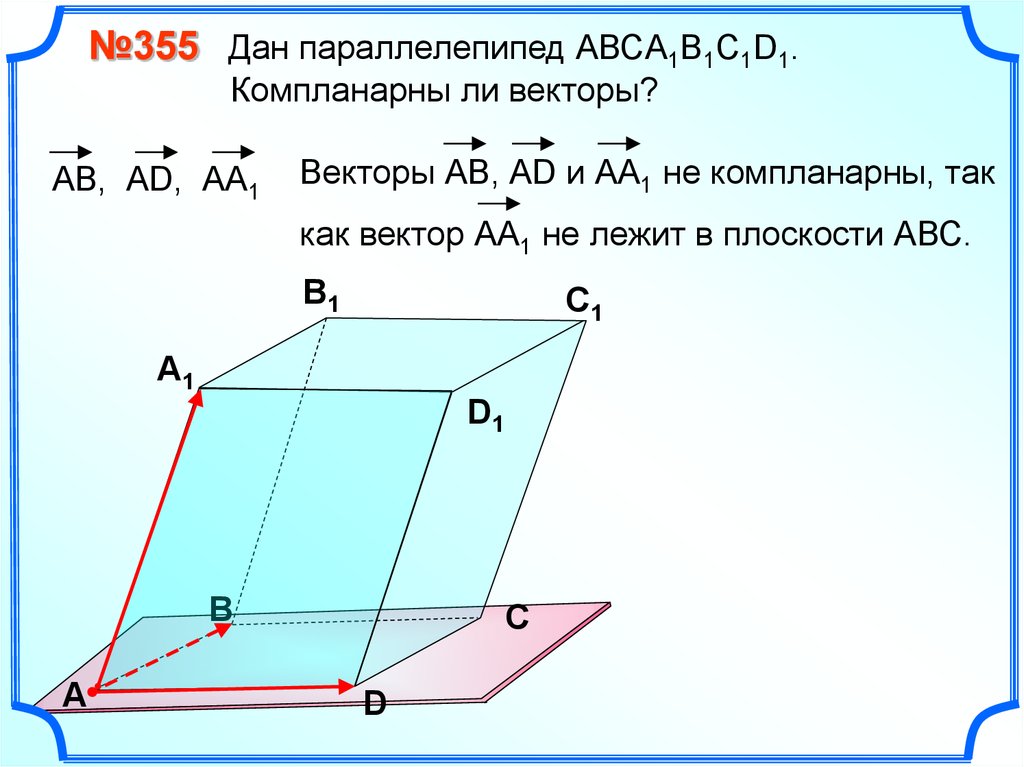
№355 Дан параллелепипед АВСA1B1C1D1.Компланарны ли векторы?
АВ, АD, АА1
Векторы АВ, АD и АА1 не компланарны, так
как вектор АА1 не лежит в плоскости АВС.
В1
С1
А1
D1
В
А
С
D
10.
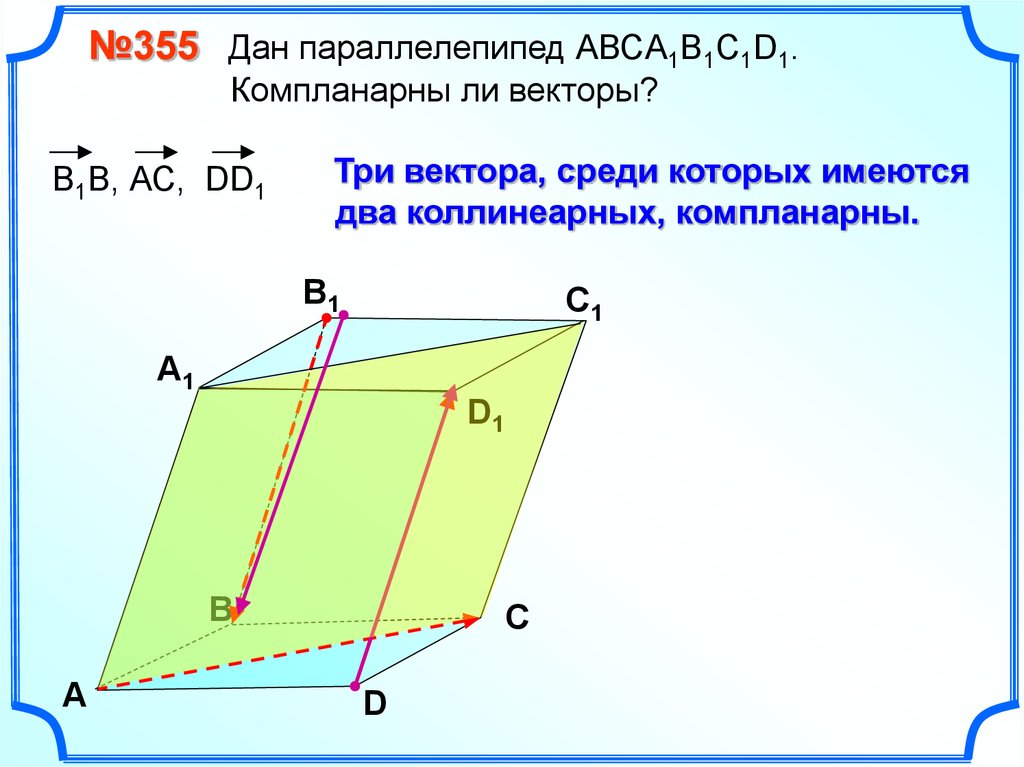
№355 Дан параллелепипед АВСA1B1C1D1.Компланарны ли векторы?
В1В, АС, DD1
Три вектора, среди которых имеются
два коллинеарных, компланарны.
В1
С1
А1
D1
В
А
С
D
11.
№355 Дан параллелепипед АВСA1B1C1D1.Компланарны ли векторы?
АD, CC1, А1B1 Векторы АВ, АD и АА1 не компланарны, так
как вектор АА1 не лежит в плоскости АВС.
В1
С1
А1
D1
Векторы АD, CC1, А1B1
не компланарны
В
А
С
D
12.
Любые два вектора компланарны.Три вектора, среди которых имеются два
коллинеарных, также компланарны.
Признак компланарности
Если вектор
a
c
можно разложить по векторам
c = xa + yb
где x и y – некоторые числа, то векторы a, b и c
и
b
, т.е. представить в виде
компланарны.
13.
Сc = xa + yb
a
В1
Докажем, что
векторы
компланарны.
А1
В
О
c
b
А
Векторы ОА и ОВ лежат в одной плоскости ОАВ.
ОА1 = х ОА
ОВ1 = у ОВ
Векторы ОА1 и ОВ1 также лежат плоскости ОАВ.
А следовательно, и их сумма – вектор ОС = х ОА + у ОВ,
равный вектору .
c
14.
Справедливо и обратное утверждение.Признак компланарности
Если векторы ,
и
компланарны, а векторы
Если вектор
можно разложить по векторам
ca b c
a
a ии b
b
cc =можно
xa + yb
разложить по векторам a и
где x и y – некоторые числа, то b
векторы a, b и c
c = xa + yb , причем
компланарны.
не коллинеарны, то вектор
, т.е. представить в виде
коэффициенты разложения определяются
единственным образом.
15.
ПО
В
Т
О
Р
И
М
Сложение векторов.
Правило треугольника.
АВ + ВС = АС
a+b
b
a
b
a
16.
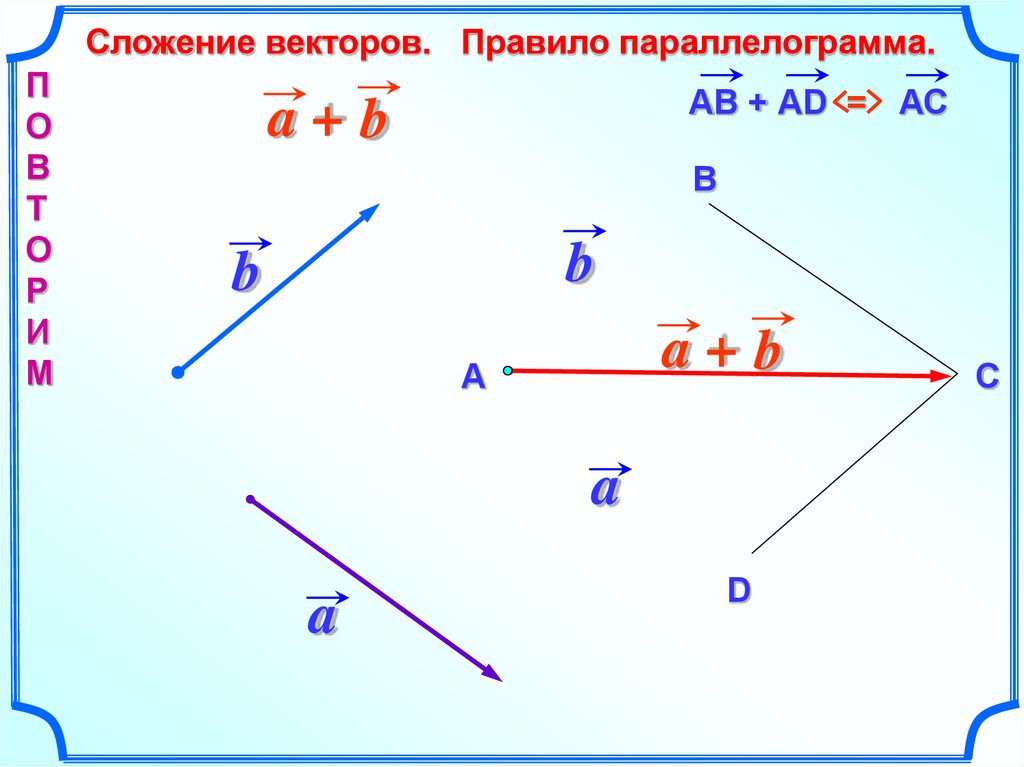
Сложение векторов. Правило параллелограмма.П
О
В
Т
О
Р
И
М
АВ + АD = АС
a+b
В
b
b
a+b
А
a
a
D
C
17.
Сложение векторов.Правило многоугольника.
П
О
В
Т
О
Р
И
М
АВ + ВС + СD + DO = АO
n
m
a
m
c
c
a
n
18.
Правило параллелепипеда. OA + OB + OC = ODиз OED
из OAE
OD = OE + ED = (OA + AE) + ED = OA + OB + OC =
D
=a+b+c
В1
С
c
Е
A
В
О
a
b
19.
№358 Дан параллелепипед АВСA1B1C1D1. Назовитевектор, начало и конец которого являются вершинами
параллелепипеда, равный сумме векторов:
АВ + АD + АА1 = AC1
D1
A1
C1
B1
D
A
С
В
20.
№358 Дан параллелепипед АВСA1B1C1D1. Назовитевектор, начало и конец которого являются вершинами
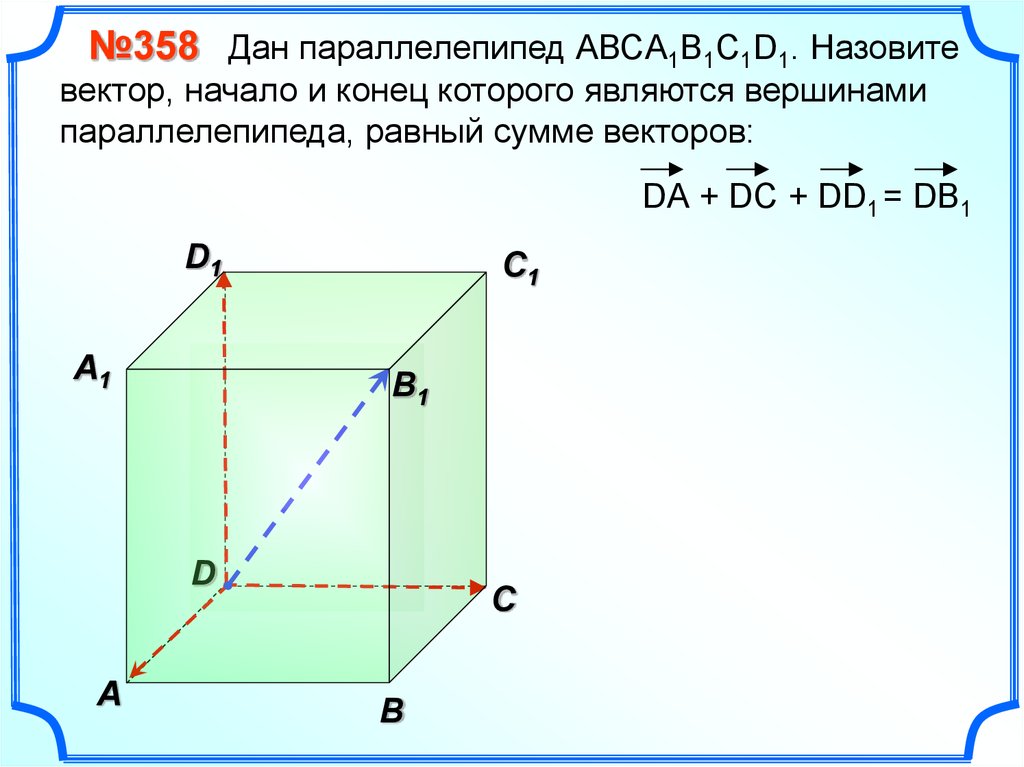
параллелепипеда, равный сумме векторов:
DА + DC + DD1 = DB1
D1
A1
C1
B1
D
A
С
В
21.
№358 Дан параллелепипед АВСA1B1C1D1. Назовитевектор, начало и конец которого являются вершинами
параллелепипеда, равный сумме векторов:
A1B1 + C1B1 + BB1
D1
A1
C1
B1
D
A
С
В
DC + DA + DD1 = DB1
22.
№358 Дан параллелепипед АВСA1B1C1D1. Назовитевектор, начало и конец которого являются вершинами
параллелепипеда, равный сумме векторов:
A1A + A1D1 + AB
D1
A1
C1
B1
D
A
С
В
A1A + A1D1 + A1B1 = A1C
23.
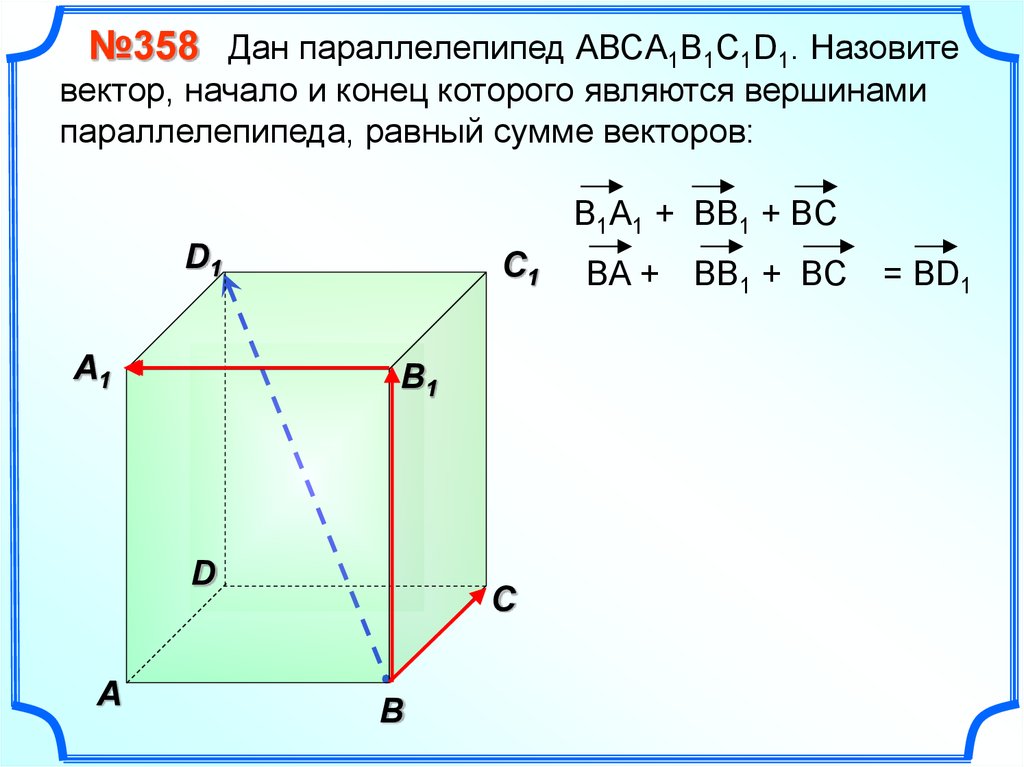
№358 Дан параллелепипед АВСA1B1C1D1. Назовитевектор, начало и конец которого являются вершинами
параллелепипеда, равный сумме векторов:
B1A1 + BB1 + BC
D1
A1
C1
B1
D
A
С
В
BA +
BB1 + BC
= BD1
24.
Разложение вектора по трем некомпланарнымвекторам. Если вектор представлен в виде
p = xa + yb + zc
z - некоторые числа, то говорят, что вектор p
разложен по векторам a , b и c . Числа x , y и z
где
x, y
и
называются коэффициентами разложения.
Теорема о разложении вектора по трем
некомпланарным векорам.
Любой вектор можно разложить по трем данным
некомпланарным векторам, причем коэффициенты
разложения определяются единственным образом.
25.
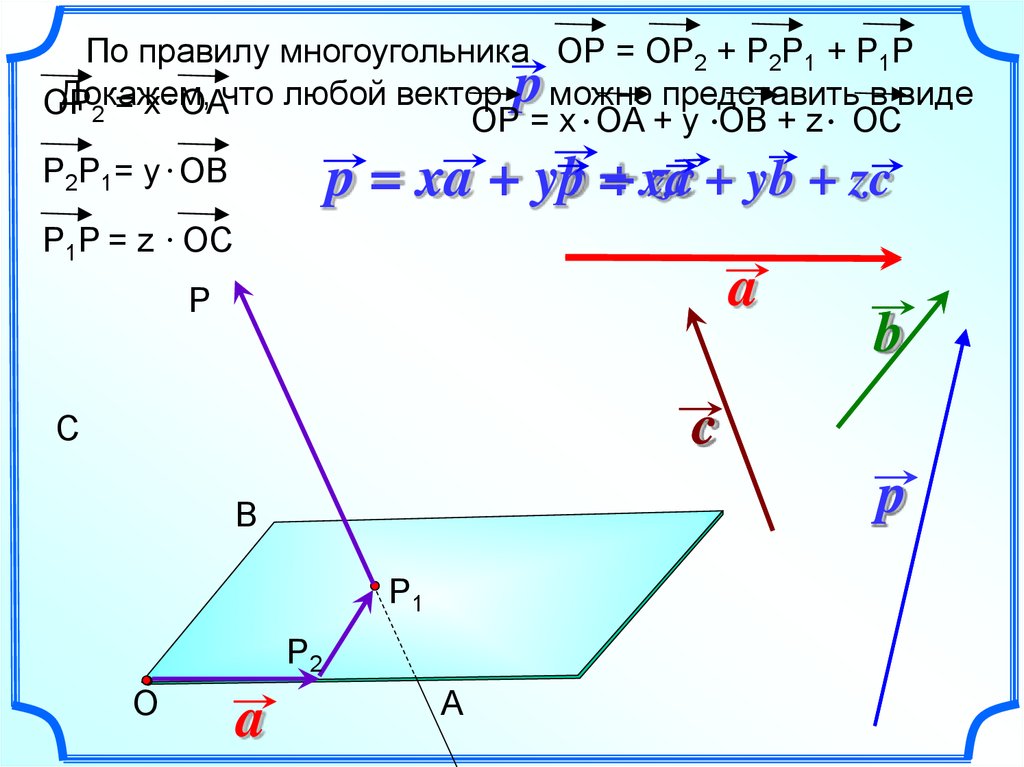
По правилу многоугольника ОР = ОР2 + Р2Р1 + Р1РДокажем,
что любой вектор можно представить в виде
ОР
2 = x OA
ОР = x OA + y OB + z OC
Р2Р1= у OВ
p = xa + yb + zc
p
p = xa + yb + zc
Р1Р = z OC
a
P
b
c
C
p
B
P1
P2
O
a
A
26.
Докажем теперь, что коэффициенты разложенияопределяются единственным образом. Допустим, что это
не так и существует другое разложение вектора
–
p = xa
x1a++yb
y1b+ +zcz1c
Это равенство выполняется
только тогда,
когда
o = (x – x1)a + (y – y1)b + (z – z1)c
Если предположить, например, что z z1 0, то из этого
o
o
o
x x1 y y1
a
b
равенства можно найти с
z z1
z z1
Тогда векторы a , b и c компланарны. Это противоречит
условию теоремы. Значит, наше предположение не верно,
и x x1 , y y1 , z z1. Следовательно,
коэффициенты
разложения p xa yb zc определяются
единственным образом.
27.
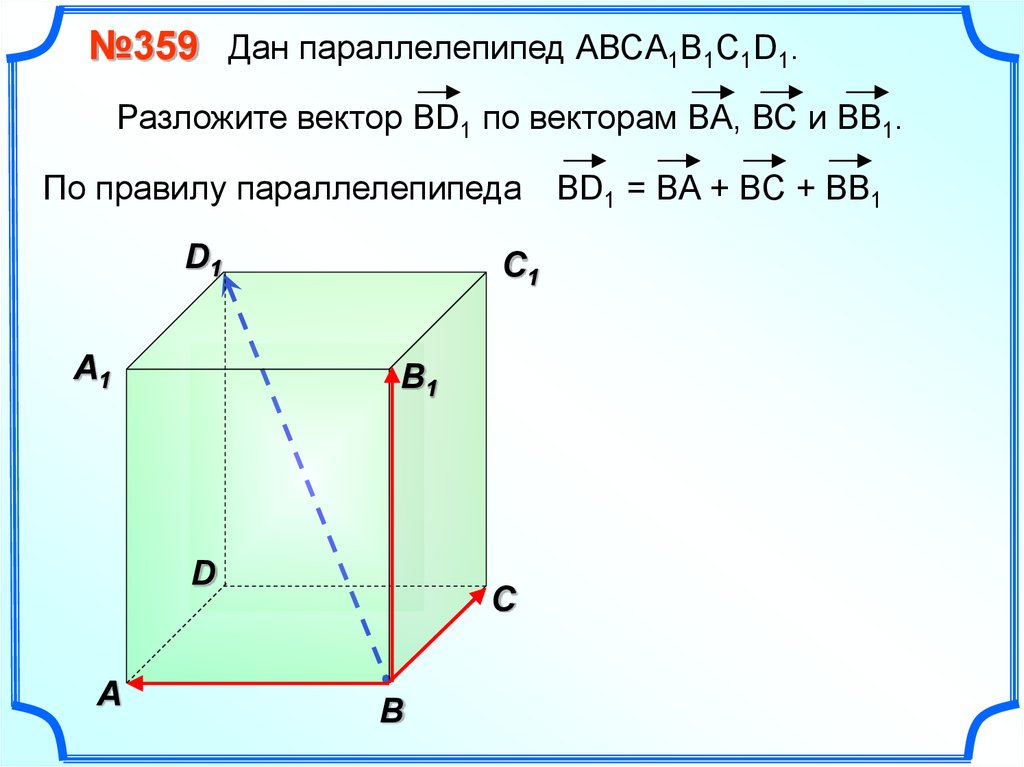
№359 Дан параллелепипед АВСA1B1C1D1.Разложите вектор BD1 по векторам BA, ВС и ВВ1.
По правилу параллелепипеда ВD1 = BA + BC + BB1
D1
A1
C1
B1
D
A
С
В
28.
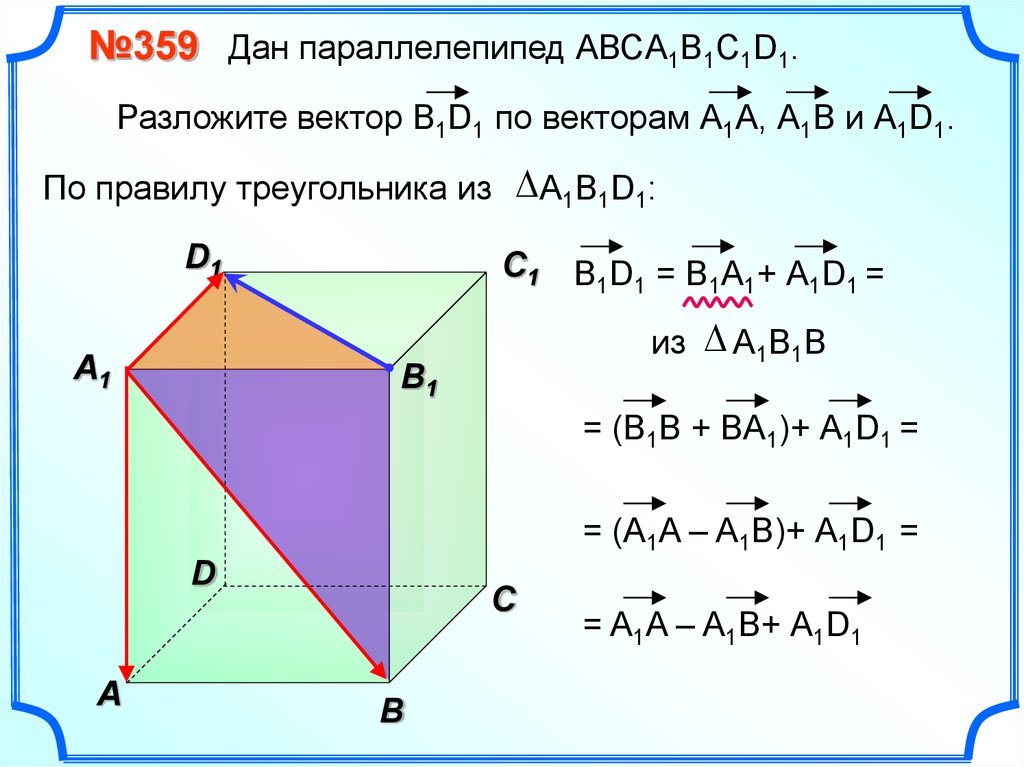
№359 Дан параллелепипед АВСA1B1C1D1.Разложите вектор B1D1 по векторам А1A, А1В и А1D1.
По правилу треугольника из А1В1D1:
D1
A1
C1
В1D1 = B1A1+ А1D1 =
из А1В1B
B1
= (В1B + BA1)+ А1D1 =
= (A1A – A1B)+ А1D1 =
D
A
С
В
= A1A – A1B+ А1D1















 mathematics
mathematics








