Similar presentations:
Линейные неравенства
1. Тема урока: Линейные неравенства 9 класс
2. Линейные неравенства
Неравенство вида ах+в≥0, где а, в - любыечисла, а≠0, называется линейным.
Например: а) 0,5х≤0
б) -3х>0
в) 2,84х-5,68˂0
г) -2х+7≥0
3. Что называется решением неравенства?
Какие из чисел являются решениемнеравенства 2х+5<7?
Х=0
5<7 является
Х=1
7<7 не является
Х = -3
-1<7 является
Корни 0 и -3 - это частные решения или
общие?
4. Свойства неравенств:
1. Любой член неравенства можноперенести из одной части неравенства в
другую с противоположным знаком, не
меняя при этом знак неравенства.
Например:
3х+6<-х+13
3х+х<-6+13
5.
Свойства неравенств:2. Обе части неравенства можно умножить
или разделить на одно и то же
положительное число не меняя при этом
знак неравенства.
Например:
а) 3х > 9
3х:3 > 9:3
х>3
б) 0,5х < 0,25
2·0,5х < 2·0,25
х < 0,5
6. Свойства неравенств:
3. Обе части неравенства можно умножитьили разделить на одно и то же
отрицательное число, изменив при этом
знак неравенства на противоположный.
Например:
а) -4х ≤ 2 | :(-4)!
х ≥ -0,5
б) -0,3х<-6 | :(-0,3)!
х > 20
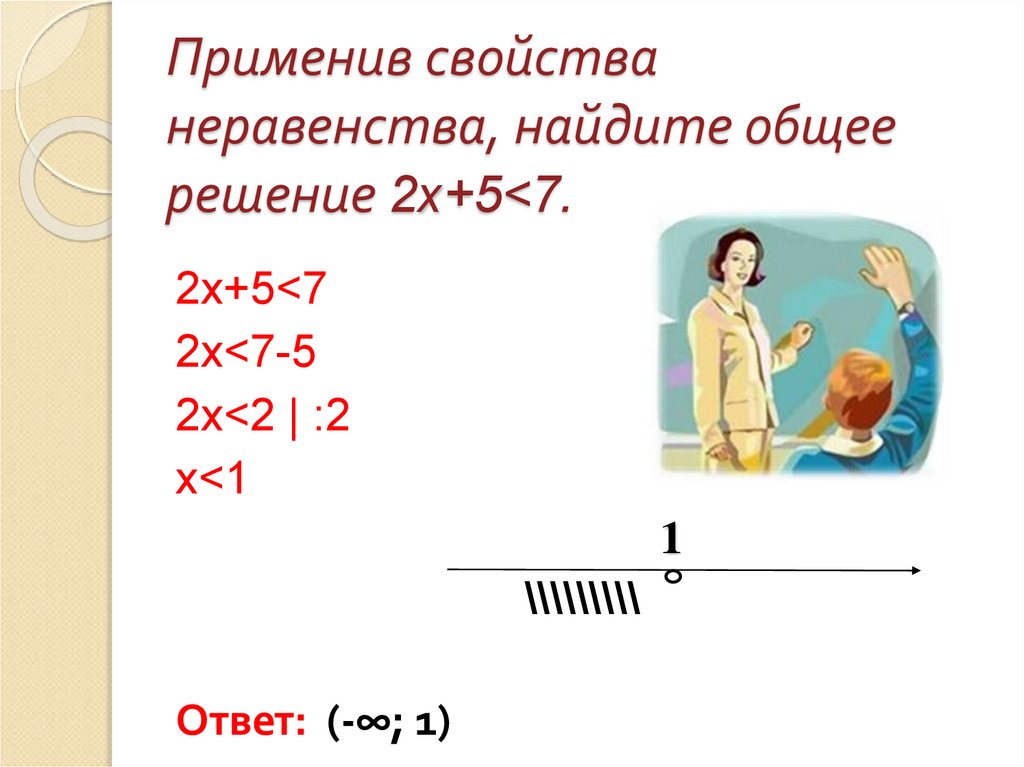
7. Применив свойства неравенства, найдите общее решение 2х+5<7.
Применив свойстванеравенства, найдите общее
решение 2х+5<7.
2х+5<7
2х<7-5
2х<2 | :2
х<1
1
\\\\\\\\\
Ответ: (-∞; 1)










 mathematics
mathematics








