Неравенства с одной переменной

1. Решение неравенств с одной переменной

8 класс п. 34 учебник Алгебра 8 класс
под ред. С.А. Теляковского М., Просвещение, 2007
Решение неравенств
с одной переменной
Определение и виды неравенств
Свойства числовых неравенств
Основные свойства равносильности неравенств
Примеры решения линейных неравенств и
неравенств, приводимых к линейным
Учитель Грязнова А.К.

2. Определение

Запись вида a > b или a < b
называется неравенством.
Неравенства вида a ≥ b, a ≤ b
называются ……
нестрогими
Неравенства вида a < b, a > b
строгими
называются ……

3. Свойства числовых неравенств

1) Если a > b, то b < a.
2) Если a > b, b > c, то a > c.
3) Если a > b, c - любое число, то a + c > b + c.
4) Если a > b, c > 0, то ac > bc.
5) Если a >b, c < 0, то ac < bc.
6) Если a > 0 b> 0, то
7) Если a > b, c > x, то a + c > b + x.
8) Если a > b, c > 0, то ac > bc.

4. Свойства равносильности неравенств

Любой член неравенства можно переносить из
одной части неравенства в другую, изменив его
знак на противоположный, при этом знак
неравенства не меняется.
Обе части неравенства можно умножить или
разделить на одно и тоже положительное
число, при этом знак неравенства не
изменится.
Если это число отрицательное, то знак
неравенства изменится на противоположное.

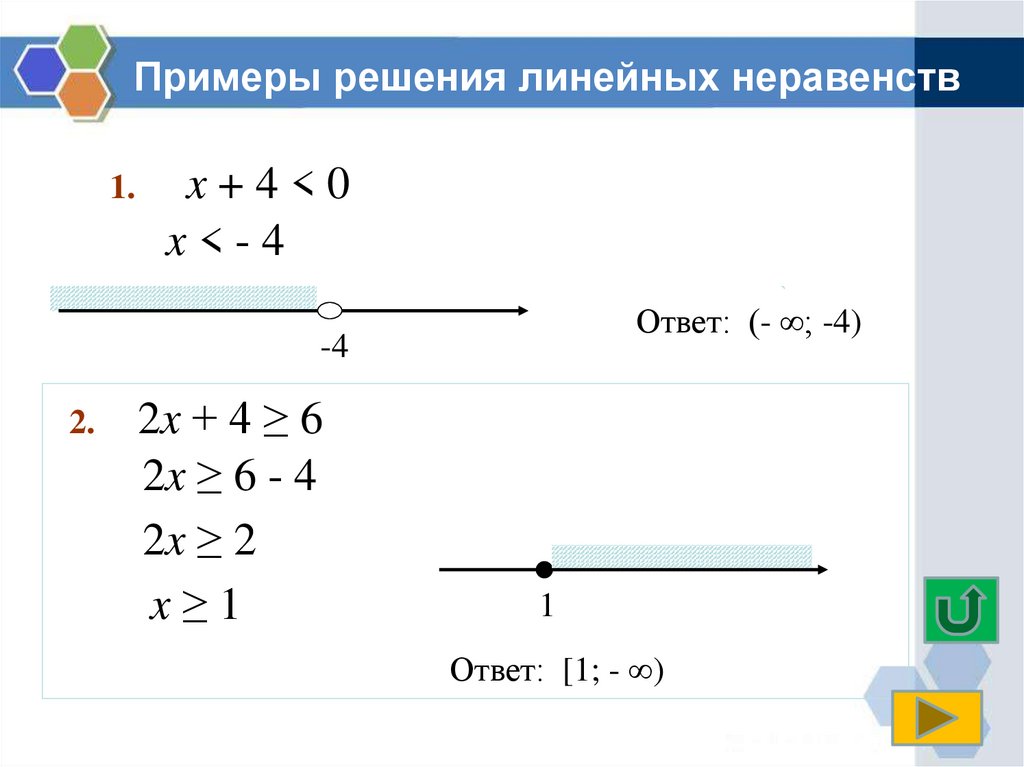
5. Примеры решения линейных неравенств

1.
x+4<0
x<-4
Ответ: (- ∞; -4)
-4
2.
2x + 4 ≥ 6
2x ≥ 6 - 4
2x ≥ 2
x≥1
1
Ответ: [1; - ∞)

6. Реши линейные неравенства

1)
х + 2 ≥ 2,5х-1;
1
2)
х - 0,25(х + 4) + 0,5(3х - 1) > 3;
2
3)
х² + х < х(х - 5) + 2
3
4)
4
5)
9 x 2 10 x 2
2.
10
9
5

7. 1) Решение

1)
1)
Решение
х + 2 ≥ 2,5х-1
х – 2,5 х ≥ -1 - 2
– 1,5 х ≥ -3
: (-1,5)
х≤2
x
2
Ответ: (- ∞; 2]

8. 2) Решение

2)
2)
Решение
х - 0,25(х + 4) + 0,5(3х - 1) > 3
х - 0,25х - 1 + 1,5х – 0,5 > 3
х - 0,25х + 1,5х > 3+1+0,5
2,25х > 4,5
х >2
x
2
Ответ: (2; +∞)

9. 3) Решение

3)
3)
Решение
х² + х < х(х - 5) + 2
х² + х < х2- 5х + 2
х² + х - х2 – 5х < 2
- 4х < 2
x
Ответ: (
; +∞ )

10. 4) Решение

4х – 16 – 9х + 15 ≥ 24
: (-5)
x
-5
Ответ: (-∞ ; -5 ]

11. 5) Решение

9 x 2 10 x 2
2.
10
9
x
Ответ: (-∞;
]

12. Реши задачи

I. Найдите
наибольшее целое число, являющееся
решением неравенства
2(х-3) - 1-3(х-2) - 4(х+1) > 0
II. Найдите
наименьшее целое число,
являющееся решением неравенства
0,2(2х+2) - 0,5(х-1) < 2
Найдите наименьшее натуральное число,
являющиеся решением неравенства
III.
3х - 3 < 1,5х + 4

13. Реши задачу I.

I. Найдите
наибольшее целое число, являющееся
решением неравенства
2(х-3) - 1-3(х-2) - 4(х+1) > 0
2х - 6 - 1- 3х + 6 - 4х - 4 > 0
-5х - 5 > 0
-5х > 5
х < -1
х
-3
-2
-1
x (-∞; -1)
Ответ: -2

14. Реши задачи II.

II. Найдите
наименьшее целое число,
являющееся решением неравенства
0,2(2х+2) - 0,5(х-1) < 2
0,4х + 0,4 - 0,5х +0,5 < 2
- 0,1х + 0,9 < 2
- 0,1х < 2 – 0,9
- 0,1х < 1,1
х > - 11
x
-11
-10 -9
x
Ответ: - 10.
(-11; +∞)

15. Реши задачи III.

Найдите наименьшее натуральное число,
являющиеся решением неравенства
III.
3х - 3 < 1,5х + 4
3х - 1,5х < 4+3
1,5х < 7
х<
х
1
x
(-∞;
2
3
4
), натуральные решения 1; 2; 3;4.
Ответ: 1

16. До встречи. Успехов в учёбе

Кто круга от квадрата не может отличить,
Тому мы с математикой советуем дружить
Нет лучше тренировки для вашего ума
Смекалки и сноровки прибавит вам она
Любому, кто стремится учиться лишь на «5»
Конечно, пригодится уменье рассуждать

17. Используемые материалы

1.Учебник Алгебра 8 класс под ред. С.А. Теляковского М., Просвещение, 2007
2. Математика. 5-11 классы. Практикум. (Дрофа) учебное электронное издание.
3. Картинка математика
http://st03.kakprosto.ru//images/article/2013/5/26/1_52553bc3a42bb52553bc3a42f9.jpg
4. Картинка Учитель http://pozitiv11.ru/wp-content/uploads/Nash-uchitel-dorogoy.jpg