Линейные неравенства с одной переменной и их решение

1. ЛИНЕЙНЫЕ НЕРАВЕНСТВА С ОДНОЙ ПЕРЕМЕННОЙ И ИХ РЕШЕНИЕ

2. Определение

Запись вида a > b (a ≥ b) или a < b
(a ≤ b ) называется неравенством.
Неравенства вида a ≥ b, a ≤ b
называются ……
нестрогими
Неравенства вида a < b, a > b
называются ……
строгими

3. Свойства равносильности неравенств

Любой член неравенства
можно переносить из одной
части неравенства в другую с
противоположным знаком,
НЕ МЕНЯЯ при этом знак
самого неравенства:
2х + 8 ≥ 4х + 7
2х – 4х ≥ 7 – 8

4. Свойства равносильности неравенств

Обе части неравенства можно
умножить или разделить на
одно и тоже положительное
число, не меняя при этом знак
самого неравенства.
5х – 15 < 0 | · 5
25х – 75 < 0
5х – 15 < 0 | : 5
х–3<0

5. Свойства равносильности неравенств

Обе части неравенства можно
умножить или разделить на одно
и тоже отрицательное число,
изменив при этом знак неравенства
на противоположный.
–6х > 12 | · (– 6)
36х < – 72
–6х > 12 | : (– 6)
х <–2

6. Алгоритм решения неравенств первой степени с одной переменной

• РАСКРЫТЬ СКОБКИ (ПРИ ИХ НАЛИЧИИ – ПО УСЛОВИЮ)
• СГРУППИРОВАТЬ СЛАГАЕМЫЕ С ПЕРЕМЕННОЙ В ЛЕВОЙ
ЧАСТИ НЕРАВЕНСТВА, А БЕЗ ПЕРЕМЕННОЙ – В ПРАВОЙ
ЧАСТИ, ПРИ ПЕРЕНОСЕ МЕНЯЯ ЗНАКИ.
• ПРИВЕСТИ ПОДОБНЫЕ СЛАГАЕМЫЕ.
• РАЗДЕЛИТЬ ОБЕ ЧАСТИ НЕРАВЕНСТВА НА КОЭФФИЦИЕНТ
ПРИ ПЕРЕМЕННОЙ, ЕСЛИ ОН НЕ РАВЕН НУЛЮ.
• ИЗОБРАЗИТЬ МНОЖЕСТВО РЕШЕНИЙ НЕРАВЕНСТВА НА
КООРДИНАТНОЙ ПРЯМОЙ.
• ЗАПИСАТЬ ОТВЕТ В ВИДЕ ЧИСЛОВОГО ПРОМЕЖУТКА.

7. ЧИСЛОВОЙ ПРОМЕЖУТОК или ИНТЕРВАЛ (ПРАВИЛЬНАЯ ЗАПИСЬ ОТВЕТА НЕРАВЕНТСВА)

1. Если по условию неравенство – НЕСТРОГОЕ, то
ответ записывают в круглых скобках, например,
ответ неравенства – (– ;5).
2. Если по условию неравенство – СТРОГОЕ, то
ответ записывают в квадратных скобках, например,
ответ неравенства – [8;5].
3. Бесконечность и минус бесконечность в любом
неравенстве ВСЕГДА записываются с КРУГЛОЙ скобкой.

8. УСТНАЯ РАБОТА

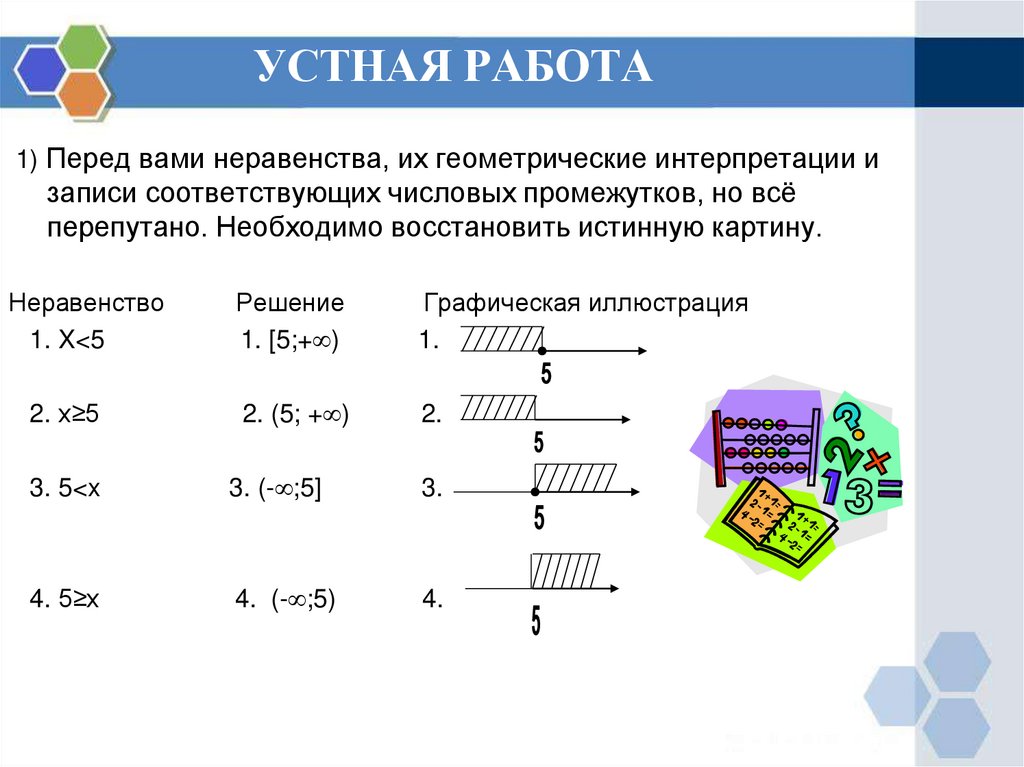
1) Перед вами неравенства, их геометрические интерпретации и
записи соответствующих числовых промежутков, но всё
перепутано. Необходимо восстановить истинную картину.
Неравенство
1. X<5
Решение
1. [5;+ )
Графическая иллюстрация
1.
2. x≥5
2. (5; + )
2.
3. 5<x
3. (- ;5]
3.
4. 5≥x
4. (- ;5)
4.

9. УСТНАЯ РАБОТА

2) Какие из указанных чисел 2; 5; 11; 7 являются
решениями неравенства 2х-15>0 ?
3) « Найди ошибку!»
а) х≥ 7
Ответ: (-∞;7)
б) у< 2,5
Ответ: (-∞;2,5]
в) m≥ 12
Ответ: (-∞;12)
г) -3k≤ 3,9; k≤ -1,3
Ответ: (-∞; -1,3)

10. Поисковая работа

Решить неравенство:
1)
х - 0,25(х + 4) + 0,5(3х - 1) > 3;
2)
х² + х < х(х - 5) + 2.

11. Решение:

1)
х - 0,25(х + 4) + 0,5(3х - 1) > 3
х - 0,25х - 1 + 1,5х – 0,5 > 3
х - 0,25х + 1,5х > 3+1+0,5
2,25х > 4,5
х >2
x
2
Ответ: (2; +∞)

12. Решение:

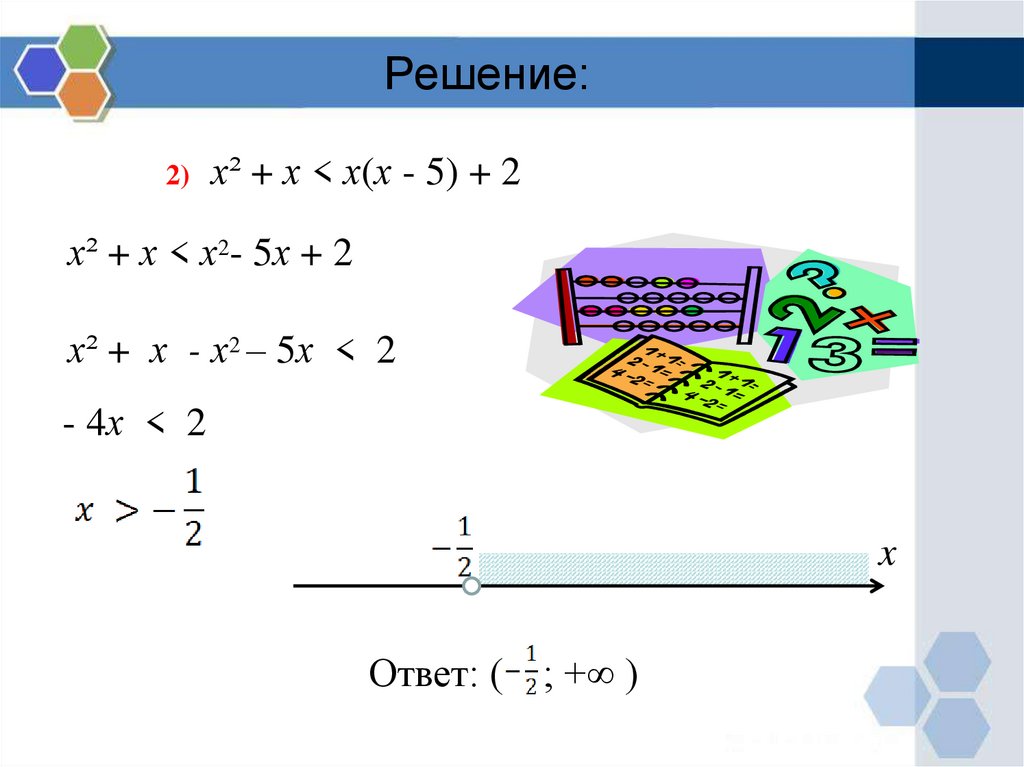
2)
х² + х < х(х - 5) + 2
х² + х < х2- 5х + 2
х² + х - х2 – 5х < 2
- 4х < 2
x
Ответ: (
; +∞ )

13. Домашняя работа:

Решить неравенства
1) 2х≥18
2) -4х>16
3) 3х≤21
4) -5х<35
5) 17х-2≤12х-1
6) 3(3х-1)>2(5х-7)
7) 3-9х≤1-х
8) 5(х+4)<2(4х-5)