Степень с натуральным показателем

1.

2.

Верны ли утверждения?
1.
2.
3.
4.
5.
6.
нет
Произведение двух отрицательных чисел всегда отрицательно.
Произведение двух чисел с разными знаками всегда
да
отрицательно.
Произведение двух противоположных чисел равно 0. нет
Произведение десяти отрицательных множителей да
положительно.
Произведение семнадцати множителей , из которых девять
положительные, а восемь отрицательные, положительно. да
Произведение шести отрицательных множителей, двух
нет
положительных множителей и 0 положительно.

3.

Укажите знак произведения:
1) -12 ∙ 47∙ (-1) ∙ 2,3;
+
2) -4 ∙ (-1,2) ∙ (-25);
−
3) (-1) ∙ (-3) ∙ (-5) ∙ (-7) ∙ (-9);
−
4) 1 ∙ (-2) ∙ (-3) ∙ (-0,4) ∙ (-2,6); +
5) 24 ∙ (-8) ∙ (-6) ∙ (-5,2) ∙ (-7) ∙ 31 ∙ (-9) ∙ (-2).
+

4.

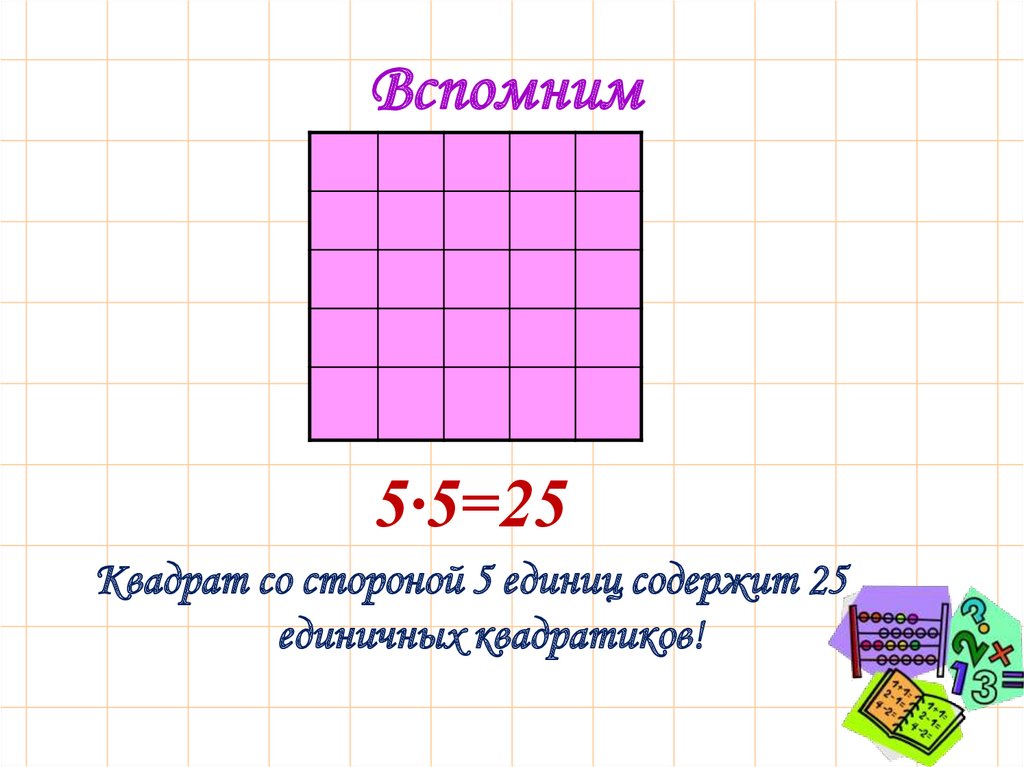
Вспомним
5∙5=25
Квадрат со стороной 5 единиц содержит 25
единичных квадратиков!

5.

Вспомним
5∙5∙5=125
Куб со стороной 5 единиц содержит 125
единичных кубиков

6.

Вспомним
Произведение 5∙5 обозначают
5∙5 =5²
(читается: «Пять в квадрате»)
Произведение 5∙5∙5 обозначают
5∙5∙5 =5³
(читается : «Пять в кубе»)

7.

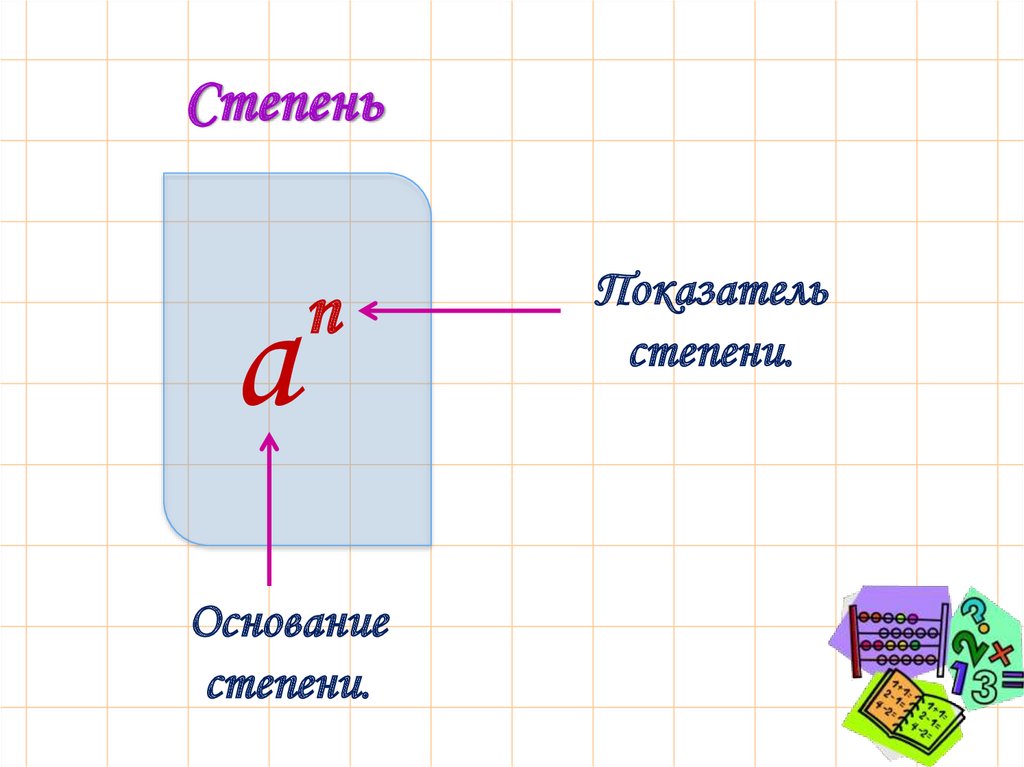
Степень

8.

Древнеегипетская задача:
У семи лиц по семи кошек, каждая кошка
съедает по семи мышей, каждая мышь съедает по
семи колосьев, из каждого колоса может вырасти
по семь мер ячменя.
Сколько мер ячменя сохранится благодаря этим
кошкам?

9.

Решение:
Количество кошек:
Количество мышей:
Количество колосьев:
7 ∙ 7= 49
7 ∙ 7 ∙ 7 = 343
7 ∙ 7 ∙ 7 ∙ 7 = 2401
Количество мер ячменя:
7 ∙ 7 ∙ 7 ∙ 7 ∙ 7 = 16807

10.

Проблема!
Как можно проще записать полученные произведения?
2
7∙7= 7
3
7
7∙7∙7=
7 ∙ 7 ∙ 7 ∙ 7 = 74
5
7∙7∙7∙7∙7= 7
Запись: 7 ∙ 7 ∙ 7 ∙ 7 ∙ 7 =75
читается так «7 в степени 5» или
«7 в пятой степени».

11.

Определения
1. Степенью числа а с натуральным показателем
n, большим 1, называется произведение n
множителей, каждый из которых равен а.
аⁿ= а∙а∙а∙…∙а
n раз
2. Степенью числа а с показателем 1
называется само число а:
а¹ =а

12.

Степень
а
n
Основание
степени.
Показатель
степени.

13.

Нахождение значения степени называется
возведением в степень.
Примеры
Возвести в степень.
26 = 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 = 64
2,52 = 2,5 ∙ 2,5 = 6,25
(3/4)4 = (3/4)∙ (3/4)∙ (3/4)∙ (3/4) =81/256

14.

Сделаем выводы:
• При возведении в степень нуля получается…
нуль.
• При возведении в степень единицы получается…
единица.
• При возведении в степень положительного числа
получается… положительное число.
• При возведении в степень отрицательного числа
получается…
положительное число, если показатель
четное число, отрицательное, если
показатель нечетное число.

15.

Замечания
1)
0 n =0 ;
2) 1 n
=1;
> 0, то аn > 0;
4) если а < 0, то аn > 0, где n – чётное;
если а < 0, то аn < 0, где n – нечётное.
3) если а