Технологии обработки информации. Лекция 1. Описательная статистика: основные понятия

1.

Технологии обработки информации
Лекция 1
Описательная статистика: основные понятия
Преподаватель: Тазиева Рамиля Фаридовна

Методы анализа данных
Статистические:
Кибернетические:
Дескриптивный анализ.
Анализ природы данных
(проверка гипотез
стационарности,
нормальности, однородности,
оценка вида функции
распределения).
Анализ
связей (корреляционный и
регрессионный
анализ, факторный
анализ, дисперсионный
анализ).
Многомерный статистический
анализ .
Методы классификации.
Кластерный анализ.
Искусственные
нейронные
сети (распознавание,
прогноз).
Деревья решений.
Методы ближайшего
соседа и k-ближайшего
соседа
Системы обработки
экспертных знаний.

4.

Генеральная и выборочная совокупности
Генеральная совокупность - вся
совокупность изучаемых объектов,
интересующая исследователя.
Выборка - часть генеральной
совокупности, определенным
способом отобранная с целью
исследования и получения
выводов о свойствах и
характеристиках генеральной
совокупности.

5.

1. Номинальная шкала
2. Порядковая шкала
3. Интервальная шкала
Виды шкал
5. Дихотомическая шкала
4. Относительная шкала

6.

Основные понятия
Случайной величиной X называется величина, которая в результате
опыта (или испытания) принимает какое-либо значение
Пусть в результате независимых испытаний, проведенных в одинаковых
условиях, получены числовые значения признака X{x(1),x(2), …,x(n)}, где
n—объем выборки.
Статистикой называется некоторая произвольная функция от выборки.
Вариационным рядом (статистическим распределением) называется
ранжированный в порядке возрастания (или убывания) ряд вариант:x1, x2,
. . .,xn(x1≤x2≤ . . . ≤xn).
Варианты,xi
x1
x2
...
xk
Частоты,ni
n1
n2
...
nk

7.

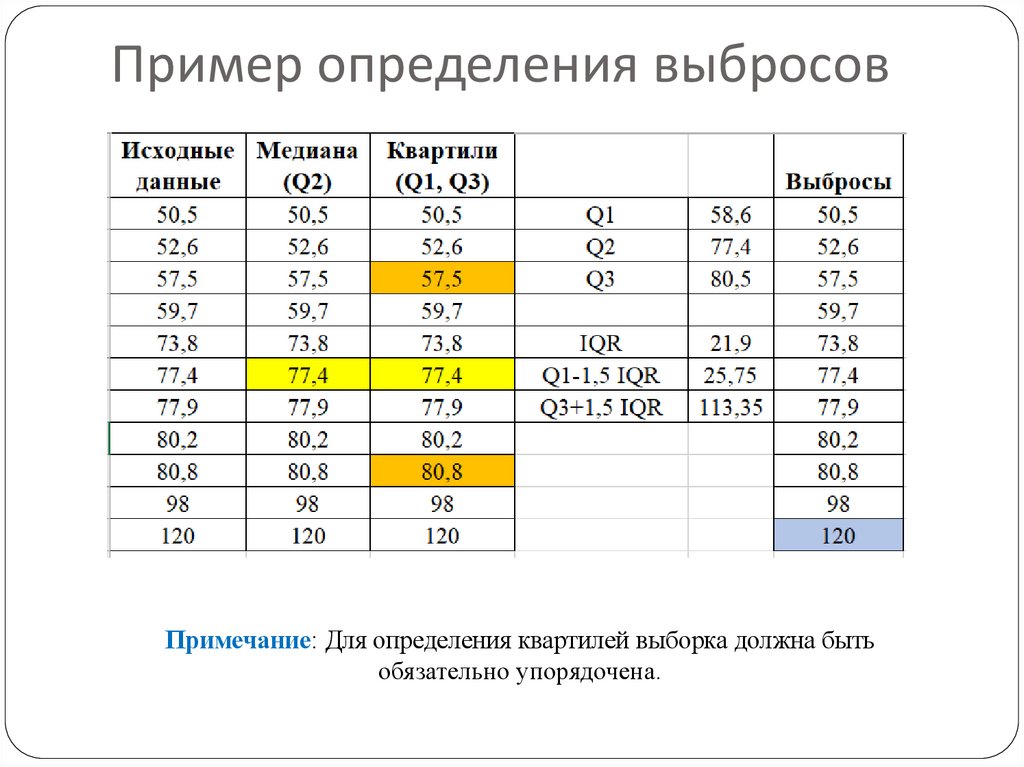
Выбросы. Квартили
Выброс — это нетипичное наблюдение, то есть такое наблюдение,
которое существенно отличается от остальных в выборке.
Что делать с выбросами? Их можно удалить перед подсчетом
описательных статистик и отдельно упомянуть в отчёте, что такие
наблюдения были.
Квартили — это такие значения, которые делят вариационный ряд на
четыре равные части (по 25 % в каждой).
o
Q1 Нижний квартиль отделяет 25 % наблюдений с наименьшими
значениями от остальных 75 %.
o
Q2 Второй квартиль — это медиана (делит вариационный ряд
попалам).
o
Q3 Верхний квартиль отделяет 25 % наблюдений с наибольшими
значениями от остальных 75 %.
Межквартильный размах (IQR) — это разность между третьим и первым
квартилем.
В этом нам помогут квартили и межквартильный размах. Выбросом
считается значение в следующих случаях:
o
o
Если наблюдение меньше, чем значение нижнего
квартиля минус межквартильного размаха. Q1-1.5 IQR
Если наблюдение больше, чем значение верхнего
квартиля плюс межквартильного размаха. Q3+1.5 IQR

8.

Пример определения выбросов
Примечание: Для определения квартилей выборка должна быть
обязательно упорядочена.

9.

Интервальный вариационный ряд
1. Вычисляют размах R варьирования признака Х как разность между
наибольшим xmax и наименьшим xmin значениями признака:
R =xmax-xmin.
2. Размах R варьирования признака Х делится на k равных частей. Число k
выбирают, пользуясь одним из следующих правил:
k n
k 1 log 2 n 1 3,221 lg n
3. Длина h каждого частичного интервала определяется по формуле: h=R/k.
4. За начало x0 первого интервала рекомендуется[6] брать величину x0=xmin0,5h.
5. Конец xk последнего интервала находят по формуле xk=xmax+0,5h.
Вариантыинтервалы,
( xi-1 ;xi )
Частоты,ni
[x0 ; x1]
( x1 ;x2]
...
( xk-1; xk]
n1
n2
...
nk

10.

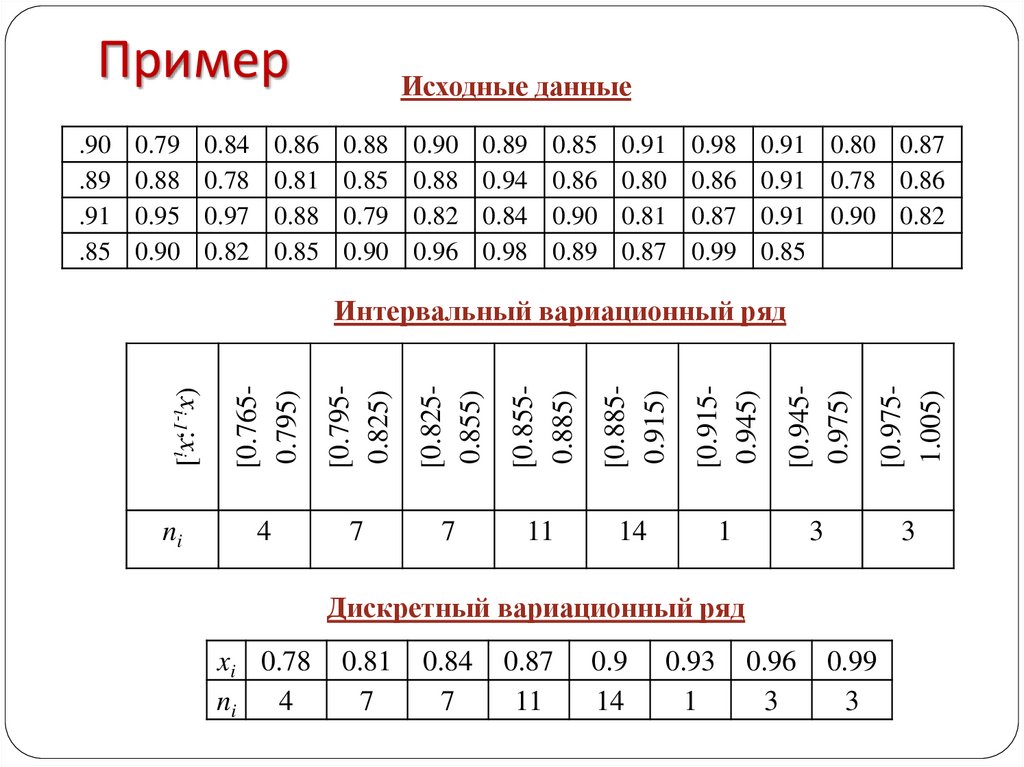
Пример
0.79
0.88
0.95
0.90
0.84
0.78
0.97
0.82
0.86
0.81
0.88
0.85
0.88
0.85
0.79
0.90
0.90
0.88
0.82
0.96
0.89
0.94
0.84
0.98
0.85
0.86
0.90
0.89
0.91
0.80
0.81
0.87
0.98
0.86
0.87
0.99
0.91 0.80 0.87
0.91 0.78 0.86
0.91 0.90 0.82
0.85
[0.8250.855)
[0.8550.885)
[0.8850.915)
[0.9150.945)
[0.9450.975)
[0.9751.005)
(xi-1;xi]
ni
[0.7950.825)
Интервальный вариационный ряд
[0.7650.795)
.90
.89
.91
.85
Исходные данные
4
7
7
11
14
1
3
3
Дискретный вариационный ряд
xi 0.78
ni 4
0.81
7
0.84
7
0.87
11
0.9
14
0.93
1
0.96
3
0.99
3

11.

Построение интервального вариационного
ряда
1. Рассчитаем размах варьирования:
,
R xmax xmin 0.99 0.78 0.21
где xmin – наименьшая варианта данной выборочной совокупности;
.
xmax – наибольшая варианта данной выборочной совокупности.
2. Вычислим число равных частей, на которое нужно разделить размах
варьирования:
k n 50 7
3. Вычислим шаг h (длину интервалов):
R 0.21
h
0.03
k
7
4. Вычислим начальное значение первого интервала x0 и конечное значение
последнего интервала xk:
x0 xmin 0.5 h 0.78 0.5 0.03 0.765
xk xmax 0.5 h 0.99 0.5 0.03 1.005

12.

Гистограмма и полигон
Гистограммой называется ступенчатая фигура, для построения которой по
оси абсцисс откладывают отрезки, изображающие частичные интервалы (xi1;xi) варьирования признака Х, и на этих отрезках, как на основаниях, строят
прямоугольники с высотами, равными частотам соответствующих
интервалов.
Частоты
Частоты
Полигоном называется ломанная соединяющая точки с координатами (xi;ni).
Варианты-интервалы
Варианты

13.

Кумулятивная кривая
.
Варианты xi
x1
x2
…
xk
Относительные
частоты
wi= ni / n
w1 = n 1 / n
w2= n2/ n
…
wk= nk / n
Накопленные
относительные
частоты
Wi= Wi-1 + wi
W1= w1
(W0=0)
W2= W1 + w2
…
Wk=Wk-1 + wk
Эмпирическая функция
распределения
1
F ( x ) ni ,
n xi x
*
n

14.

Центральная тенденция
Выборочная средняя
1 n
x xi ,
n i 1
k
1 k
x xi ni , n ni ,
n i 1
i 1
x 0.8724.
Свойства среднего
• При расчете среднего не допускаются пропущенные значения данных.
• Информативность среднего значения переменной высока, если известен
ее доверительный интервал.
• С увеличением размера выборки точность оценки среднего возрастает.
• С увеличением разброса значений выборки надежность среднего падает.
Примечание: При анализе данных средним не следует злоупотреблять, необходимо
учитывать его свойства и ограничения. Известны характеристики "средняя температура
по больнице" или "средняя высота дома", показывающие некорректность использования
этой меры центральной тенденции для некоторых случаев.

15.

S M e 1
Центральная тенденция
Медианой Me называют варианту которая делит вариационный ряд на две
равные по числу вариант части.
При нечетном объеме выборки n=2k+1
xk xk 1
Me
,
2
При четном объеме выборки n=2k
xi 0.78
ni 4
0.81
7
0.84
7
0.87
11
Me=xk+1
0.9
14
0.93
1
0.96
3
0.99
3
x25 x26
Me
0.87.
2
Примечание: Для определения медианы выборка должна быть обязательно
упорядочена.

16.

Центральная тенденция
Модой Mo называют варианту, которая имеет наибольшую частоту.
xi 0.78
ni 4
0.81
7
0.84
7
0.87
11
0.9
14
0.93
1
0.96
3
0.99
3
M 0 = 0.9.
Коэффициент вариации - меры разброса признака относительно его среднего
значения.
S
V *100%.
x
V
S 0.054279
0.062218 .
0.8724
x
Примечание: Если коэффициент вариации превышает 33%, то это говорит о
неоднородности информации и необходимости исключения самых больших и
самых маленьких значений.

17.

Дисперсия
Формула расчета дисперсии для несгруппированных данных
n
n
2
1
1
2
2
2
S ( xi x) xi x
n i 1
n i 1
Формула расчета дисперсии для сгруппированных данных
k
k
2
2
2
i
i
i i
i 1
i 1
2
1
1
S ( x x) n x n x .
n
n
Если объем выборки n>50, то рассчитывают исправленную дисперсию:
n
1
2
s
(
x
x
)
,
i
n 1 i 1
2
S 2 0.002946
k
1
2
s2
(
x
x
)
ni ,
i
n 1 i 1
s 2 0.003006
Выборочное среднеквадратическое отклонение
S S 2 0.002946 0.054279 ,
s s 2 0.003006 0.05483 .

18.

Box plot

19.

Характеристики с графика boxplot
Boxplot показывает пять важных характеристических
значений для набора данных:
o
Минимум .
o
Нижний квартиль .
o
Медиана .
o
Верхний квартиль .
o
Максимум .

20.

Асимметрия
Асимметрия характеризует отклонение
относительного нормального распределения.
распределения
признака
k
As
m3
,
3
S
m3
k
1
( xi x)3 ni .
n i 1
m3
m3 - центральный момент третьего порядка
График функции плотности
распределения случайной величины с
правосторонней асимметрией
ni ( xi x) 3
i 1
n
0.00223
0.0000446.
50
As 0.278894.
График функции плотности
распределения случайной величины с
левосторонней асимметрией

21.

Эксцесс
Эксцесс – величина островершинности.
k
k
n ( x x)
4
1
m4
0.001175
m
( xi x) 4 ni . m4 i 1
E x 4 3,
0.0000235.
4
n i 1
S
n
50
m4 - центральный момент четвертого Ex 0.29274057.
порядка
( x x )2
t
1
F (t )
S 2
i
e
2S 2
dx.
i

22.

Доверительные интервалы
Для математического ожидания
s
m x t
n
x t
s
n
где, t -γ-квантиль распределения Стьюдента с n-1 степенью свободы.
Примечание: Для поиска
=СТЬЮДРАСПОБР(1- , n-1).
t
можно
воспользоваться
функцией
Excel
Для дисперсии
(n 1) s 2
22
2
p1 P ( )
2
2
1
(n 1) s 2
2
0.045802 0.068326 .
12
12 0.95
2
, 50 1
ХИ2ОБР((1 - 0,95)/2;50 - 1) = 70.2241
12 0.95
ХИ2ОБР((1 + 0,95)/2;50 - 1) = 31.55492
p 2 P( ) 1 1 .
, 50 1
2
2
2
2
2
2

23.

Распределение Стьюдента
k
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
0,2
3,08
1,89
1,64
1,53
1,48
1,44
1,41
1,40
1,38
1,37
0,36
0,36
0,35
0,34
0,34
0,34
0,33
0,33
0,33
0,33
0,1
6,31
2,92
2,35
2,13
2,02
1,94
1,89
1,86
1,83
0,81
0,80
0,78
0,77
0,76
0,75
0,75
0,74
0,73
0,73
0,72
q
0,05
12,71
4,30
3,18
2,78
2,57
2,45
2,36
2,31
2,26
2,23
2,20
2,18
2,16
2,14
2,13
2,12
2,11
2,10
2,09
2,09
0,02
31,82
6,96
4,54
3,75
3,36
3,14
3,00
2,90
2,82
2,76
2,72
2,68
2,65
2,62
2,60
2,58
2,57
2,55
2,54
2,53
0,01
63,66
9,92
5,84
4,60
4,03
3,71
3,50
3,36
3,25
3,17
3,11
3,05
3,01
2,98
2,95
2,92
2,90
2,88
2,86
2,85
0,005
127,32
14,09
7,45
5,60
4,77
4,32
4,03
3,83
3,69
3,58
3,50
3,43
3,37
3,33
3,29
3,25
3,22
3,2
3,17
3,15
0,002
318,3
22,33
10,21
7,17
5,89
5,21
4,79
4,50
4,30
4,14
4,02
3,93
3,85
3,79
3,73
3,69
3,65
3,61
3,58
3,55
0,001
636,61
31,60
12,92
8,61
6,87
5,96
5,41
5,04
4,78
4,59
4,44
4,32
4,22
4,14
4,07
4,02
3,97
3,92
3,88
3,85

24.

Распределение χ2
K
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
p
0,99
0,0002
0,02
0,12
0,30
0,55
0,87
1,24
1,65
2,09
2,56
3,05
3,57
4,11
4,66
5,23
5,81
6,41
7,01
7,63
8,26
8,90
9,54
0,95
0,004
0,1
0,35
0,71
1,15
1,64
2,17
2,73
3,33
3,94
4,57
5,23
5,89
6,57
7,26
7,96
8,67
9,39
10,1
10,9
11,6
12,3
0,90
0,02
0,21
0,58
1,06
1,61
2,20
2,83
3,49
4,17
4,87
5,58
6,3
7,04
7,79
8,55
9,31
10,1
10,9
11,7
12,4
13,2
14,0
0,50
0,46
1,39
2,37
3,36
4,35
5,35
6,35
7,34
8,34
9,34
10,3
11,3
12,3
13,3
14,3
15,3
16,3
17,3
18,3
19,3
20,3
21,3
0,25
1,32
2,77
4,11
5,39
6,63
7,84
9,04
10,2
11,4
12,5
13,7
14,8
16,0
17,1
18,2
19,4
20,5
21,6
22,7
23,8
24,9
26,0
0,10
2,71
4,61
6,25
7,78
9,24
10,6
12,0
13,4
14,7
16,0
17,3
18,5
19,8
21,1
22,3
23,5
24,8
26,0
27,2
28,4
29,6
30,8
0,05
3,84
5,99
7,81
9,49
11,1
12,6
14,1
15,5
16,9
18,3
19,7
21,0
22,4
23,7
25,0
26,3
27,6
28,9
30,1
31,4
32,7
33,9
0,025
5,02
7,38
9,35
11,1
12,8
14,4
16,0
17,5
19,0
20,5
21,9
23,3
24,7
26,1
27,5
28,8
30,2
31,5
32,9
34,2
35,5
36,8
0,01
6,63
9,21
11,3
13,3
15,1
16,8
18,5
20,1
21,7
23,2
24,7
26,2
27,7
29,1
30,6
32,0
33,4
34,8
36,2
37,6
38,9
40,3
0,005 0,001
7,88 10,8
10,6 13,8
12,8 16,3
14,9 18,5
16,7 20,5
18,5 22,5
20,3 24,3
22,0 26,1
23,6 27,9
25,2 29,6
26,8 31,3
28,3 32,9
29,8 34,5
31,3 36,1
32,8 37,7
34,3 39,3
35,7 40,8
37,2 42,3
38,6 43,8
40,0 45,3
41,4 46,8
42,8 48,3

English Русский Rules