Similar presentations:
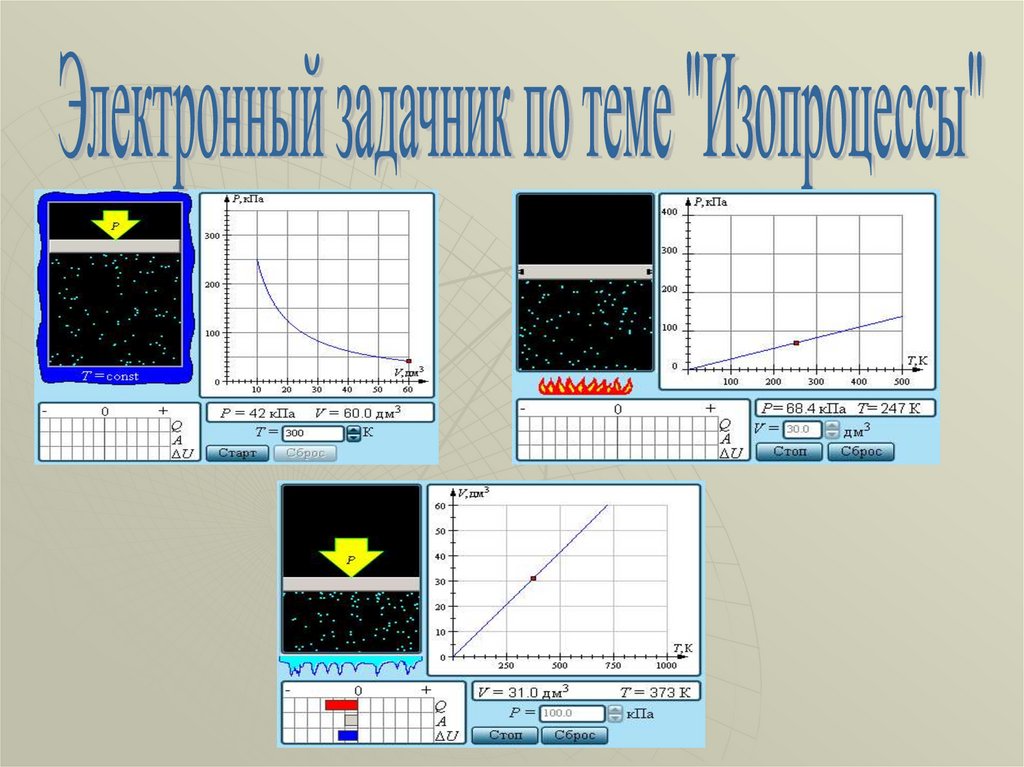
Электронный задачник по теме "Изопроцессы"
1.
2.
Задача №1.Задача №7.
Задача №2.
Задача №8.
Задача №3.
Задача №9.
Задача №4.
Задача №10.
Задача №5.
Задача №11.
Задача №6.
3.
4.
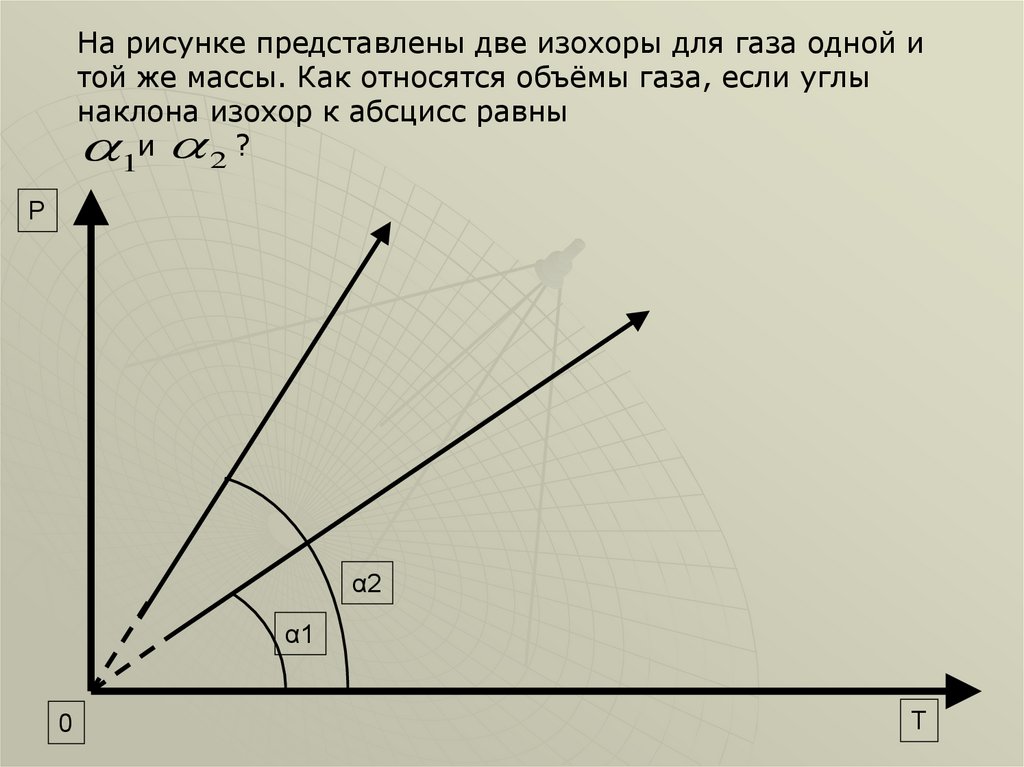
На рисунке представлены две изохоры для газа одной итой же массы. Как относятся объёмы газа, если углы
наклона изохор к абсцисс равны
и 2 ?
1
P
α2
α1
0
T
5.
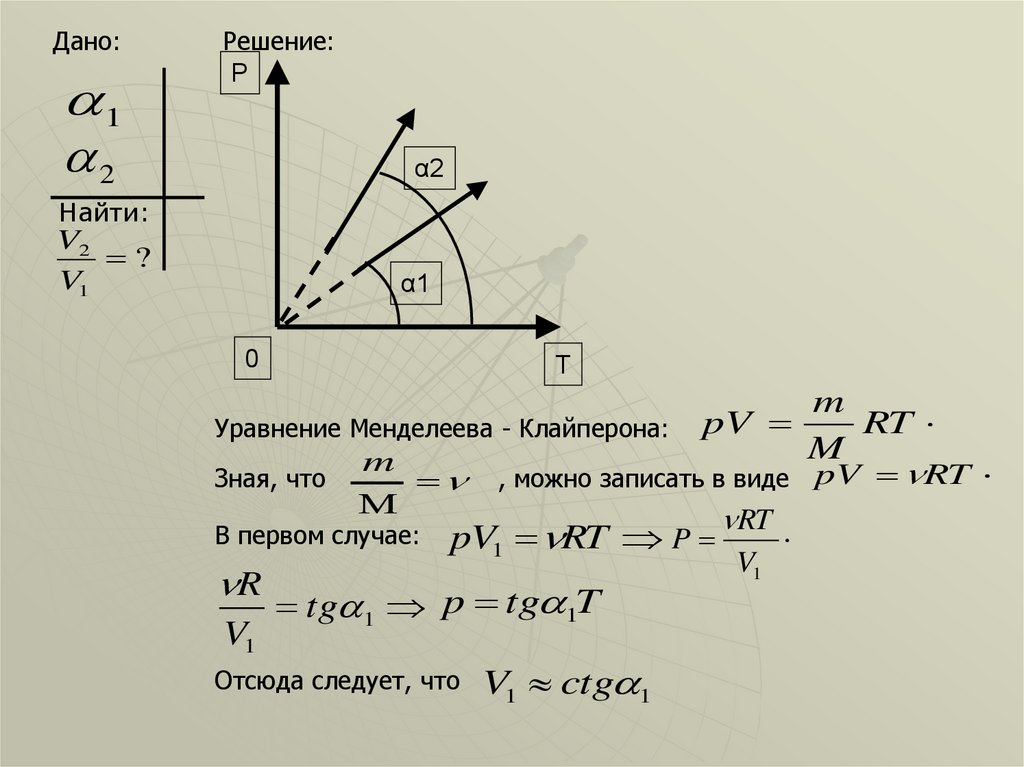
Дано:1
2
Решение:
P
α2
Найти:
V2
?
V1
α1
0
T
m
RT
Уравнение Менделеева - Клайперона: pV
M
m
Зная, что
, можно записать в виде pV RT
RT
В первом случае:
R
V1
pV1 RT P
tg 1 p tg 1T
Отсюда следует, что
V1 ctg 1
V1
6.
pV2 RT P RTV2
R
tg 2 p tg 2T V2 ctg 2
V2
Во втором случае:
Исходя из выше написанного следует, что
V2 ctg 2
V1 ctg 1
Ответ:
V2 ctg 2
V1 ctg 1
7.
8.
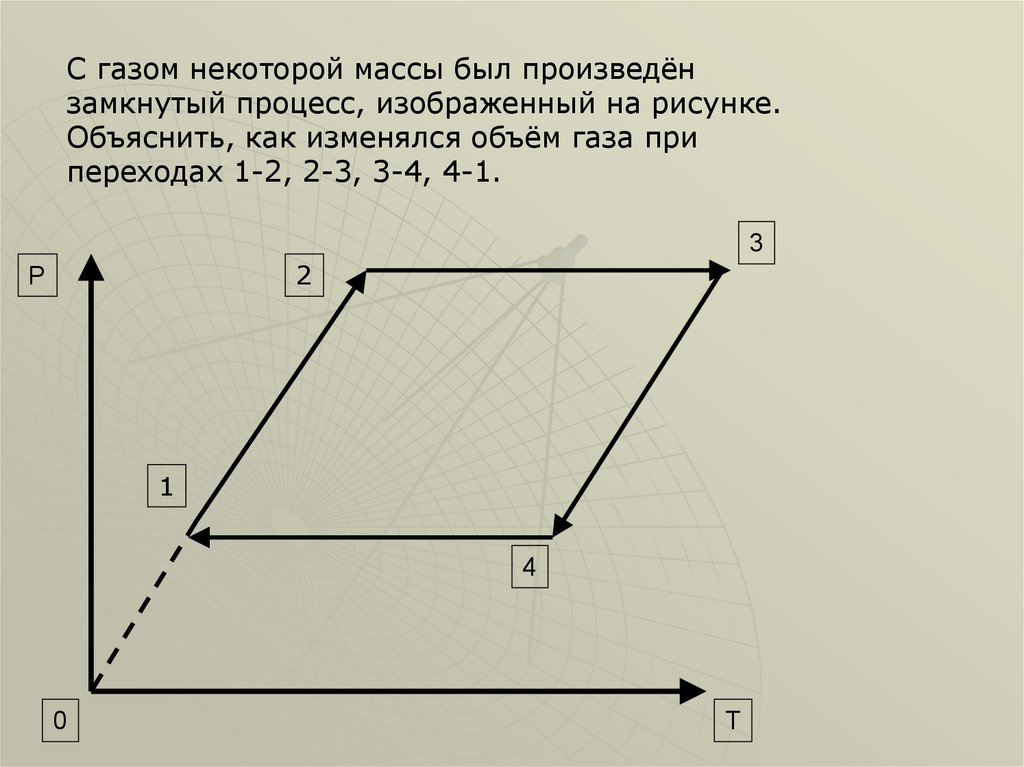
С газом некоторой массы был произведёнзамкнутый процесс, изображенный на рисунке.
Объяснить, как изменялся объём газа при
переходах 1-2, 2-3, 3-4, 4-1.
3
2
P
1
4
0
T
9.
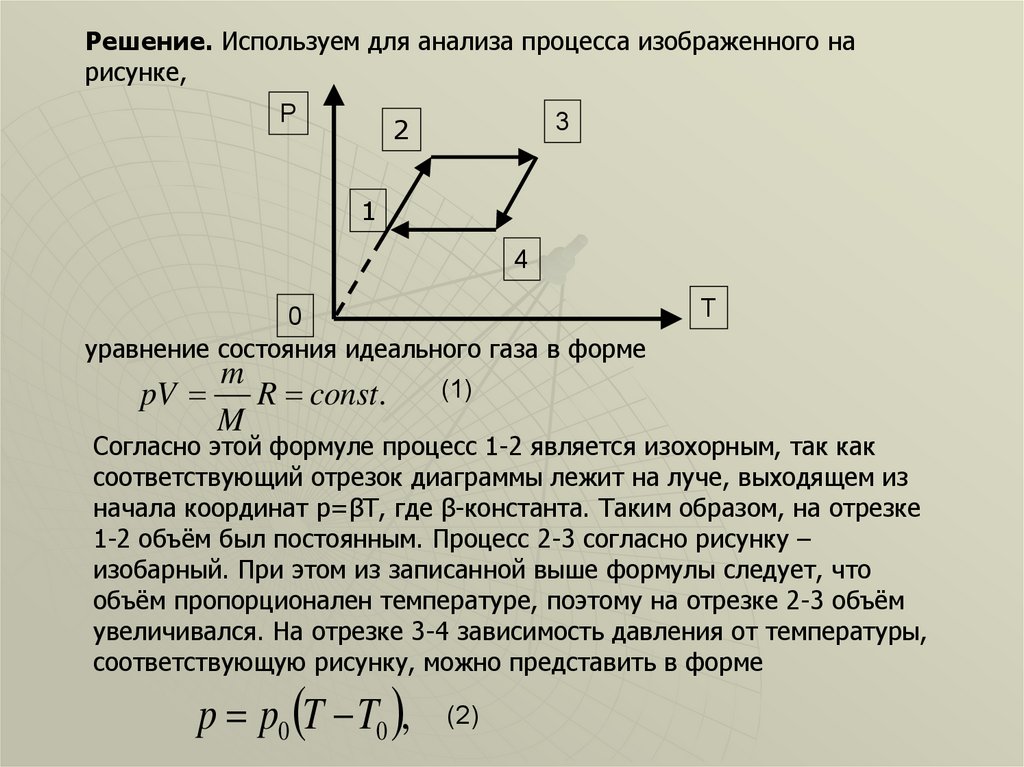
Решение. Используем для анализа процесса изображенного нарисунке,
P
3
2
1
4
0
уравнение состояния идеального газа в форме
m
pV
R const .
M
T
(1)
Согласно этой формуле процесс 1-2 является изохорным, так как
соответствующий отрезок диаграммы лежит на луче, выходящем из
начала координат p=βТ, где β-константа. Таким образом, на отрезке
1-2 объём был постоянным. Процесс 2-3 согласно рисунку –
изобарный. При этом из записанной выше формулы следует, что
объём пропорционален температуре, поэтому на отрезке 2-3 объём
увеличивался. На отрезке 3-4 зависимость давления от температуры,
соответствующую рисунку, можно представить в форме
p p0 T T0 ,
(2)
10.
где p0 и T0- положительные константы. При этом,согласно формуле (1), зависимость объёма от
температуры с учётом изменения давления (2) имеет вид:
V
mR
T
,
M p0 T T0
(3)
откуда следует, что на отрезке 3-4 объём увеличился изза уменьшения температуры.Отрезок 4-1 – вновь изобара.
Следовательно, согласно (1) здесь объём уменьшался
пропорционально уменьшению температуры.
11.
Ответ.1-2-оставался постоянным;2-3-увеличивался пропорционально Т;
3-4-увеличивался;
4-1-уменьшался пропорционально Т.
12.
13.
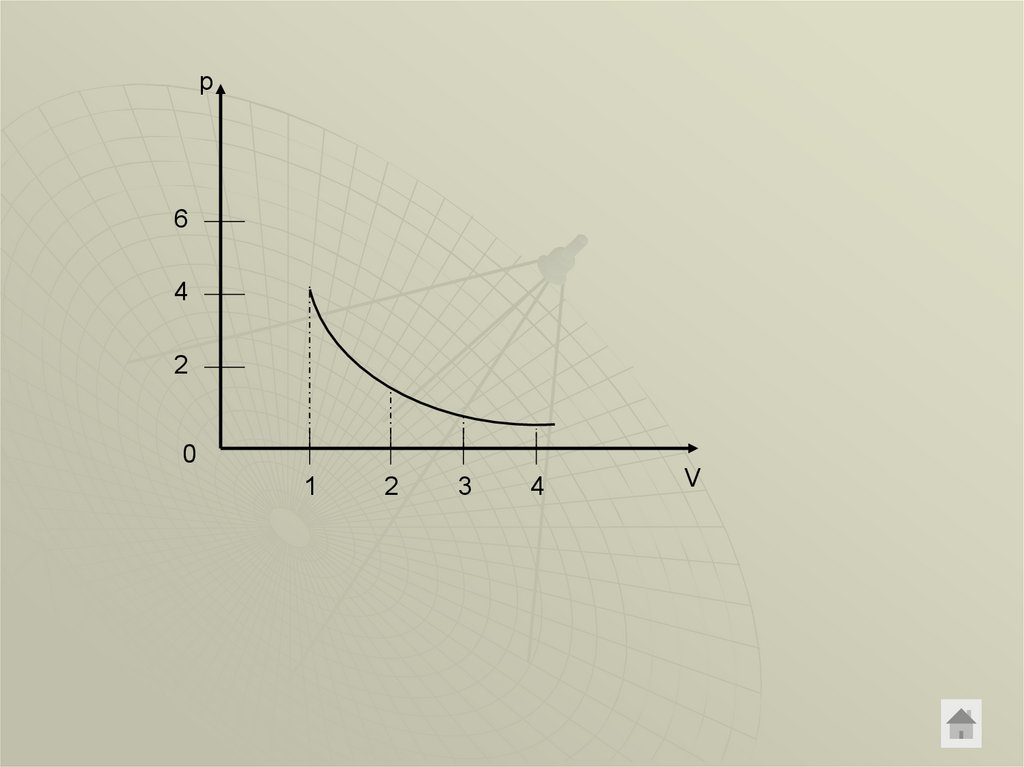
Начертить изотерму процесса для случая pV=40. Пользуясьграфиком ответить на вопрос: на сколько изменился объем
данной массы газа, если давление увеличился на 1\4
первоначальной величины.
Дано:
Решение:
pV=40
Т=const
1
p
4
p 2 p1
Найти:
p(V)=?
V ?
1
5
p1 p1
4
4
p
V
1 05
5
2 105 4 105 1,33 10
4 10 4 2 10 4 1 0 4
3 10 4
14.
p6
4
2
0
1
2
3
4
V
15.
16.
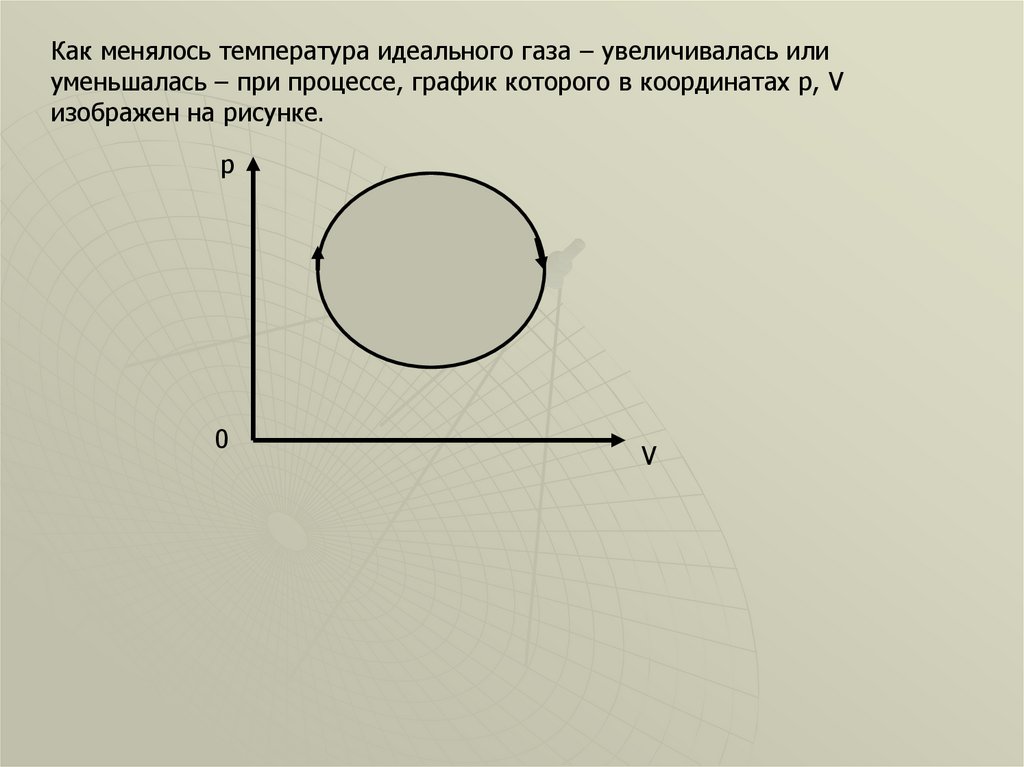
Как менялось температура идеального газа – увеличивалась илиуменьшалась – при процессе, график которого в координатах p, V
изображен на рисунке.
p
0
V
17.
Решение.p
0
н
а
г
р
в
а
н
и
е
о
х
л
а
ж
д
е
н
и
е
V
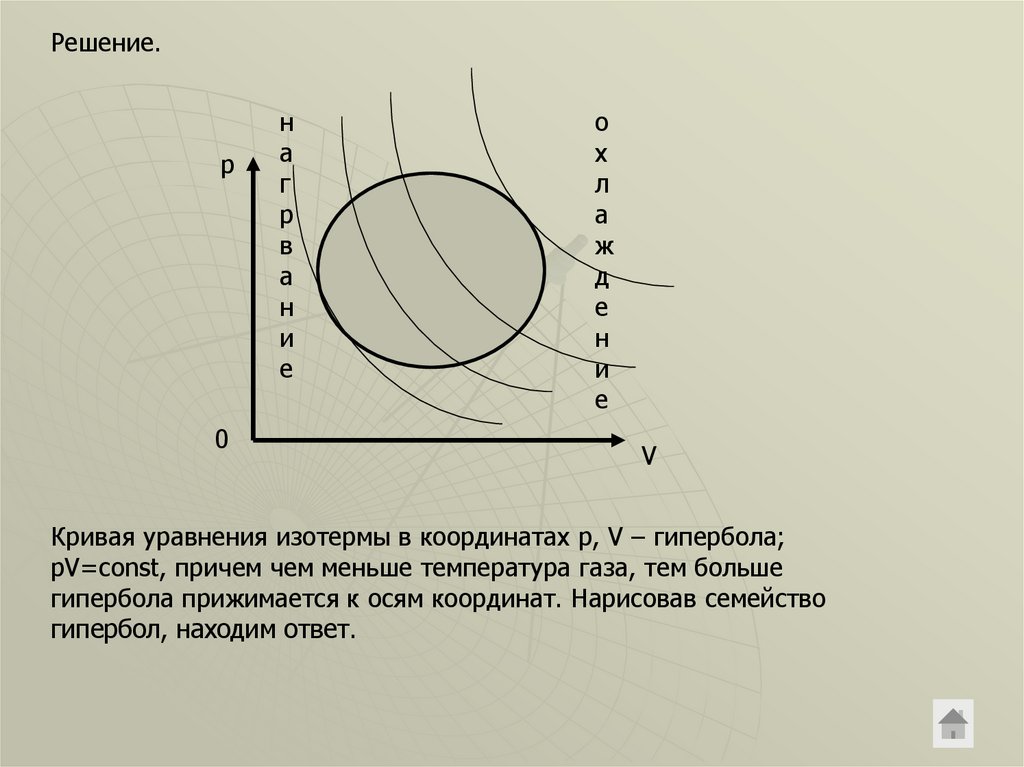
Кривая уравнения изотермы в координатах p, V – гипербола;
pV=const, причем чем меньше температура газа, тем больше
гипербола прижимается к осям координат. Нарисовав семейство
гипербол, находим ответ.
18.
19.
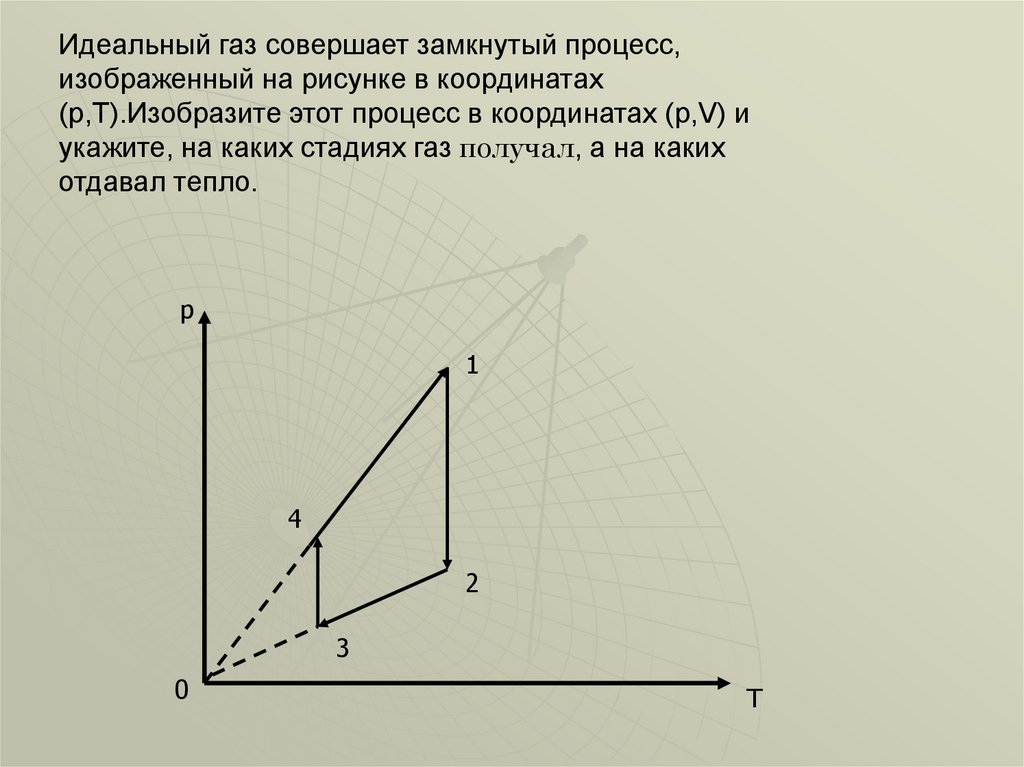
Идеальный газ совершает замкнутый процесс,изображенный на рисунке в координатах
(p,T).Изобразите этот процесс в координатах (p,V) и
укажите, на каких стадиях газ получал, а на каких
отдавал тепло.
р
1
4
2
3
0
Т
20.
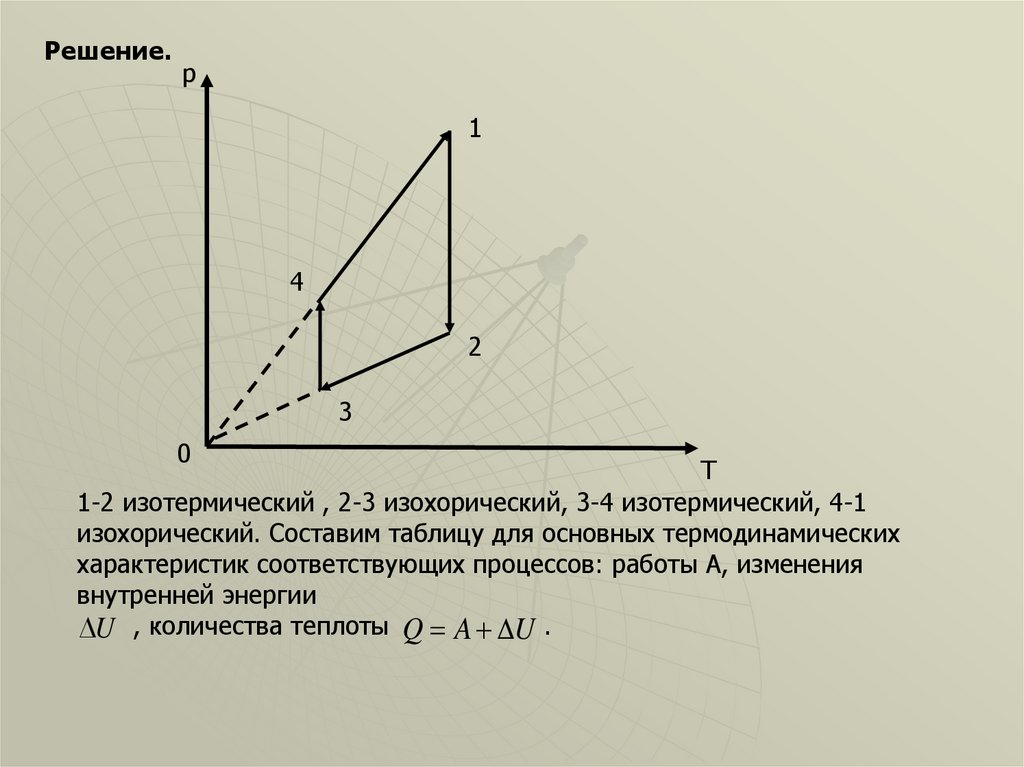
Решение.р
1
4
2
3
0
Т
1-2 изотермический , 2-3 изохорический, 3-4 изотермический, 4-1
изохорический. Составим таблицу для основных термодинамических
характеристик соответствующих процессов: работы А, изменения
внутренней энергии
U , количества теплоты Q A U .
21.
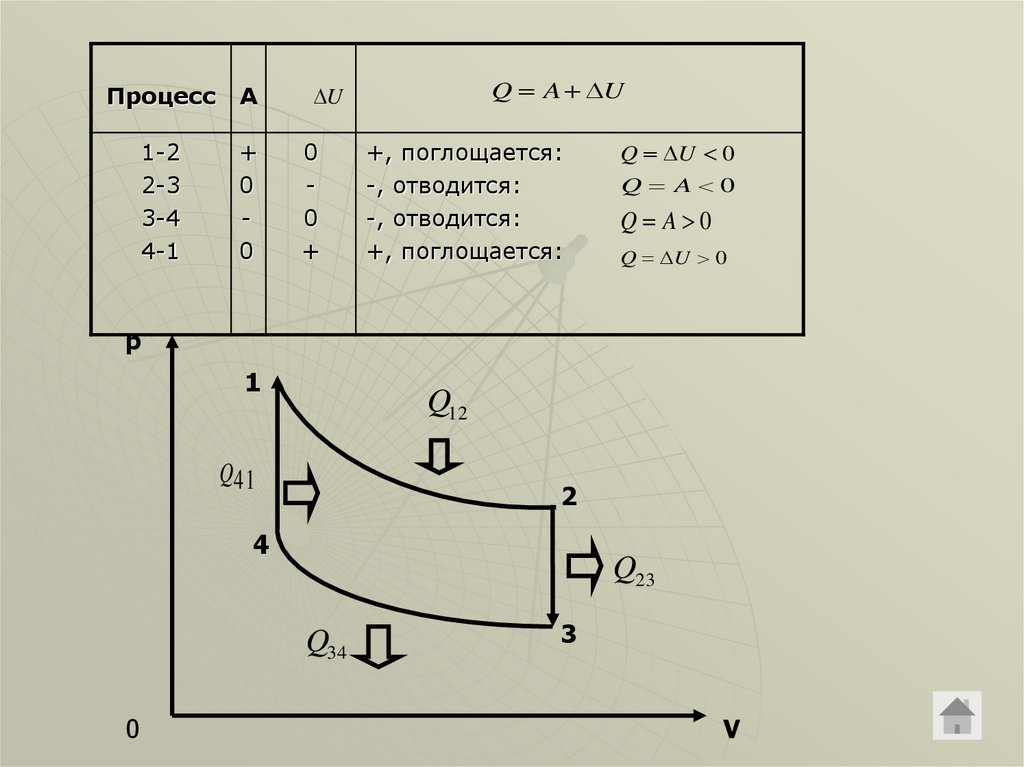
ПроцессА
1-2
2-3
3-4
4-1
+
0
0
Q A U
U
0
0
+
+, поглощается:
-, отводится:
-, отводится:
+, поглощается:
Q U 0
Q A 0
Q A 0
Q U 0
p
1
Q12
Q41
2
4
Q23
Q34
0
3
V
22.
23.
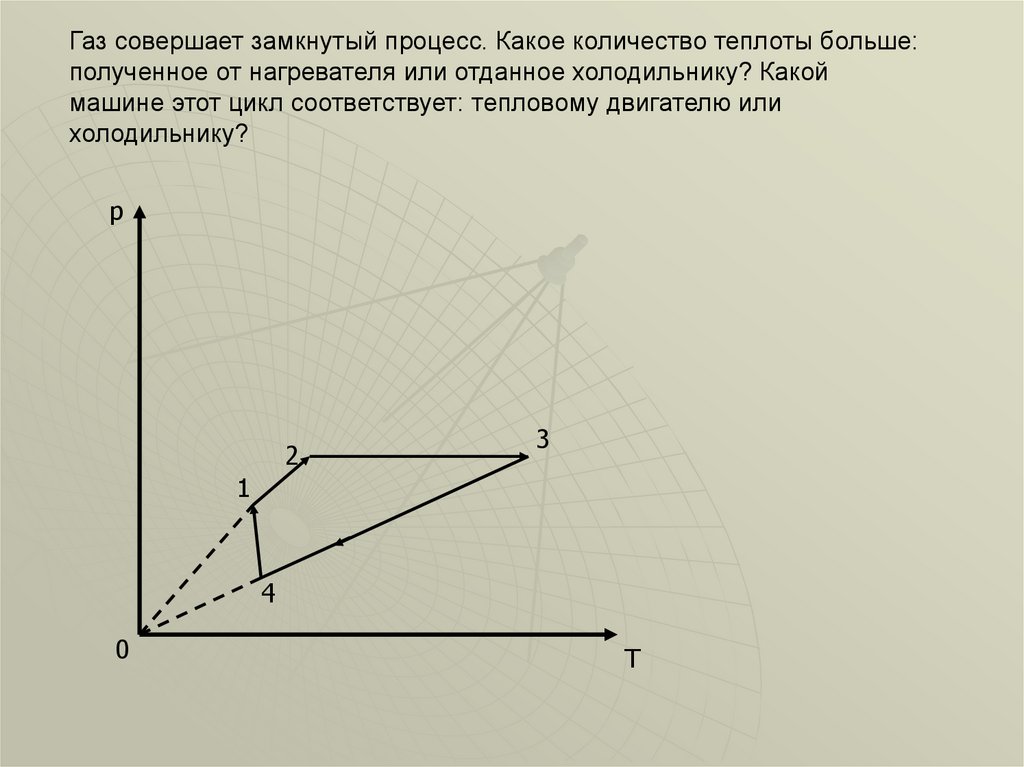
Газ совершает замкнутый процесс. Какое количество теплоты больше:полученное от нагревателя или отданное холодильнику? Какой
машине этот цикл соответствует: тепловому двигателю или
холодильнику?
р
2
3
1
4
0
Т
24.
Cформулируем общий алгоритм решения этой задачи:• перевести цикл в координаты (p, V) и составить
таблицу;
• установить направление обхода цикла и тип машины;
оценить величины поглощенного и отданного количеств
теплоты и общую работу;
• рассчитать КПД машины.
25.
Решение:p
2
Q1 2
Q23
3
Q34
1
Q41
4
0
V
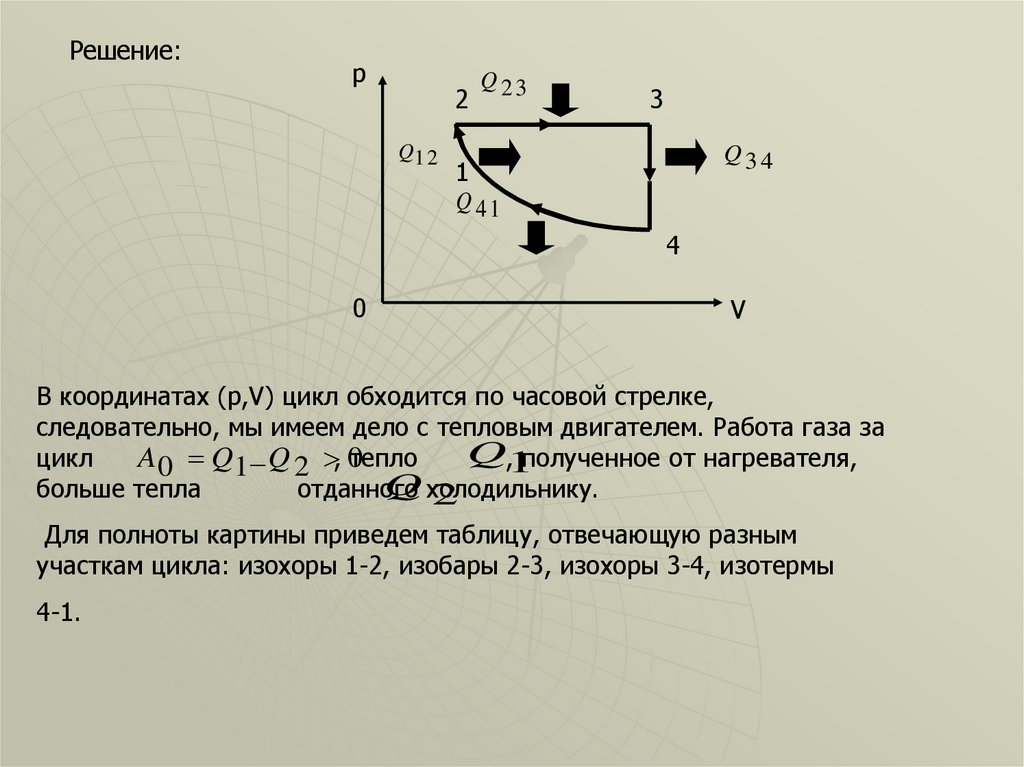
В координатах (p,V) цикл обходится по часовой стрелке,
следовательно, мы имеем дело с тепловым двигателем. Работа газа за
Q,1полученное от нагревателя,
цикл
A 0 Q1 Q 2 , 0тепло
Q холодильнику.
больше тепла
отданного
2
Для полноты картины приведем таблицу, отвечающую разным
участкам цикла: изохоры 1-2, изобары 2-3, изохоры 3-4, изотермы
4-1.
26.
Процесс1-2
2-3
3-4
4-1
Q A U
А U
0
+
0
-
+
+
0
+,
+,
-,
-,
поглощается:
поглощается:
отводится:
отводится:
Q U 0
Q A U 0
Q U 0
Q A 0
При контакте с нагревателем система получает тепло
Q1 Q1 2 Q 2 3 ,
а тепло Q 2 Q 34 Q 41 Q1 A 0 отдает холодильнику.
Если цикл запустить в обратном направлении (1 – 4 – 3 – 2 – 1 ), то
получится холодильная машина: над газом (рабочим телом)
совершается работа
A 0 A 0 0,
27.
от менее нагретого (холодного) тела забирается количествотеплоты Q1 Q14 Q 43 0 и отдается более нагретому телу
количество теплоты
Q1 Q 32 Q 21 Q 2 A 0 .
а)
Нагреватель
б)
Нагреватель
Q1
Q1
А0
Q2
Холодильник
А 0
Q2
Холодильник
28.
а) если цикл соответствует тепловому двигателю (обход по часовойстрелке), КПД равен:
Q1 Q 2
;
Q1
Q1
А0
(1)
б) если цикл соответствует идеальной тепловой машине (прямому
циклу Карно), то её КПД
T1 T 2
к
,
T1
где Т 1 и Т 2 - температуры нагревателя и холодильника
соответственно;
в) если цикл соответствует холодильной машине (обход против
часовой стрелки), то ее КПД (точнее, холодильный коэффициент)
определяется по формуле:
Q2
Q2
1
к
;
A 0
Q1 Q 2
k
(2)
29.
г) если цикл соответствует идеальной холодильной машине(обратному циклу Карно ), то ее холодильный коэффициент
Т2
1 к
к
,
Т1 Т 2
k
где Т 1 - температура более нагретого тела, Т 2 - температура
холодного тела, от которого отбирается тепло;
д) если обратный цикл соответствует так называемому
тепловому насосу, то КПД теплового насоса
Q1
1
1;
A 0
для идеального цикла Карно:
Т1
1
к
1.
Т1 Т 2
k
30.
31.
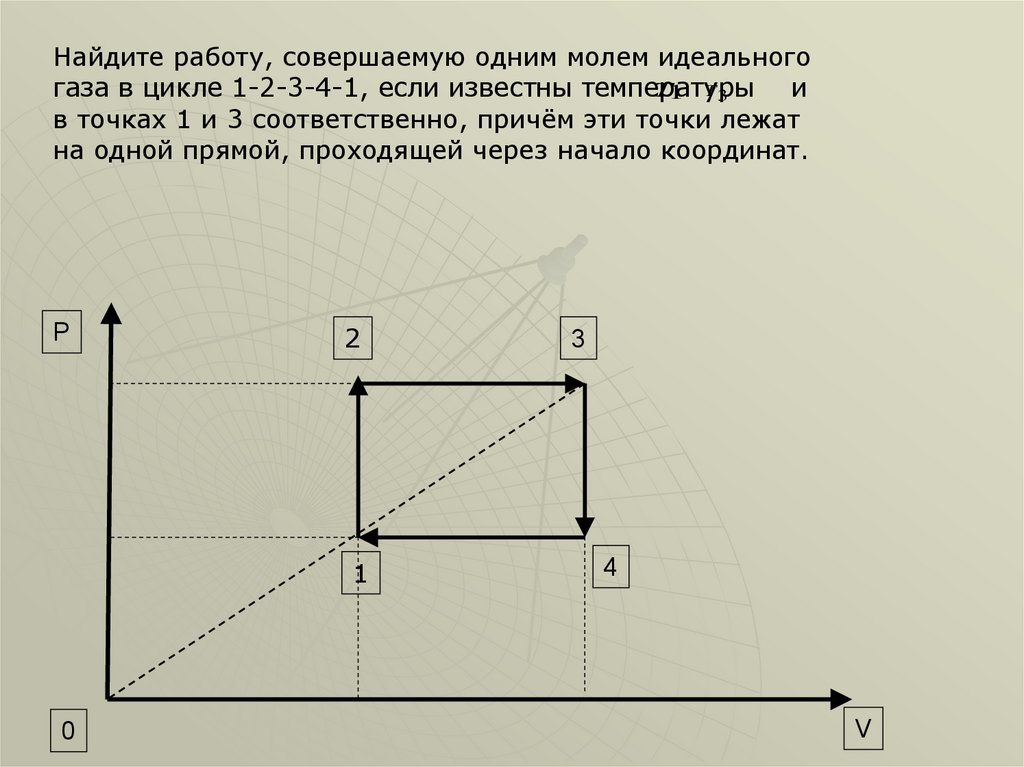
Найдите работу, совершаемую одним молем идеальногоT1 T 3
газа в цикле 1-2-3-4-1, если известны температуры
и
в точках 1 и 3 соответственно, причём эти точки лежат
на одной прямой, проходящей через начало координат.
P
2
1
0
3
4
V
32.
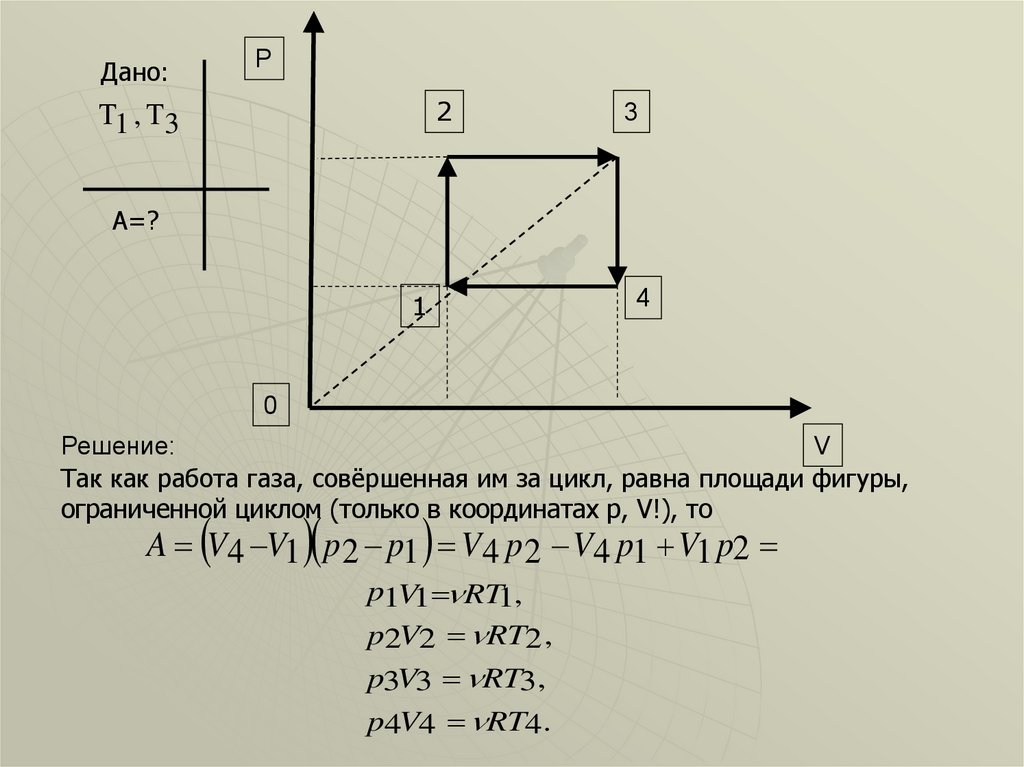
Дано:P
1 , 3
2
3
А=?
1
4
0
Решение:
V
Так как работа газа, совёршенная им за цикл, равна площади фигуры,
ограниченной циклом (только в координатах p, V!), то
A V4 V1 p 2 p1 V4 p 2 V4 p1 V1 p2
p1V1 RT1,
p2V2 RT2 ,
p3V3 RT3 ,
p4V4 RT4 .
33.
В системе уравнений:p1V1 RT1,
p2V2 RT2 ,
p3V3 RT3 ,
p4V4 RT4 .
Уменьшаем индексы:
p1V1 RT1,
p 2 V1 RT 2 ,
p 2V3 RT3 ,
p1V3 RT 4 .
(1)
(2)
(3)
(4)
Исходя из уравнения Менделеева-Клайперона, можно записать:
A V V p p V p V p V p2 V p V p V p V p
4 1 2 1 4 2 4 1 1
11 3 3 2 2 4 4
RT1 RT3 RT2 RT4 R T1 T3 T2 T4 .
Из этого равенства, а также из второго и четвёртого уравнений
последней системы сразу вытекает: T4 T2
34.
Так как точки 1 и 3 лежат на прямой, проходящей через началоp3
V
координат, то
3
p
1
V1
или после следующего уменьшения индекса,
V
2 3
p
V1
1
p
Из этого равенства, а также из второго и четвёртого уравнений
T4 T2
последней системы сразу вытекает:
Перемножив почленно первое и третье, а затем второе и
четвёртое уравнения системы:
p p
2T T
R
13
1 2V1V3
p p R 2T2T4
1 2
Получим:
Отсюда
T2T4 T1T3 , или T4 T2 T1T3
A R T1 T3 2 T1T3 R T3 T1
35.
Ответ.A R T1 T3 2 T1T3 R T3 T1
36.
37.
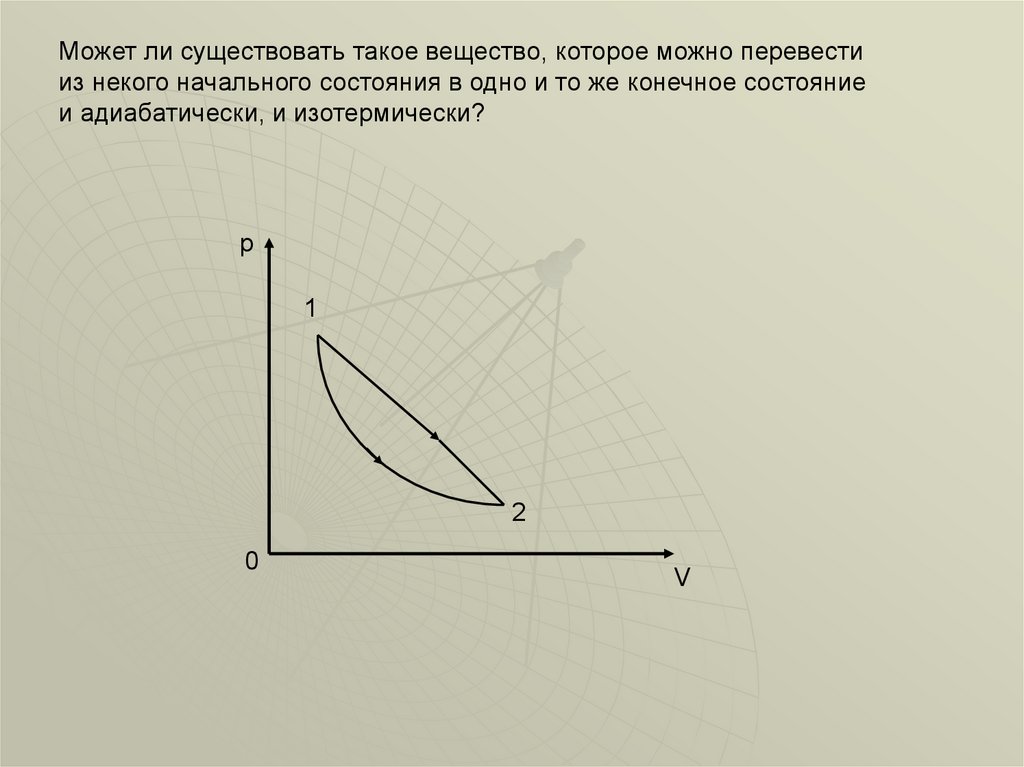
Может ли существовать такое вещество, которое можно перевестииз некого начального состояния в одно и то же конечное состояние
и адиабатически, и изотермически?
p
1
2
0
V
38.
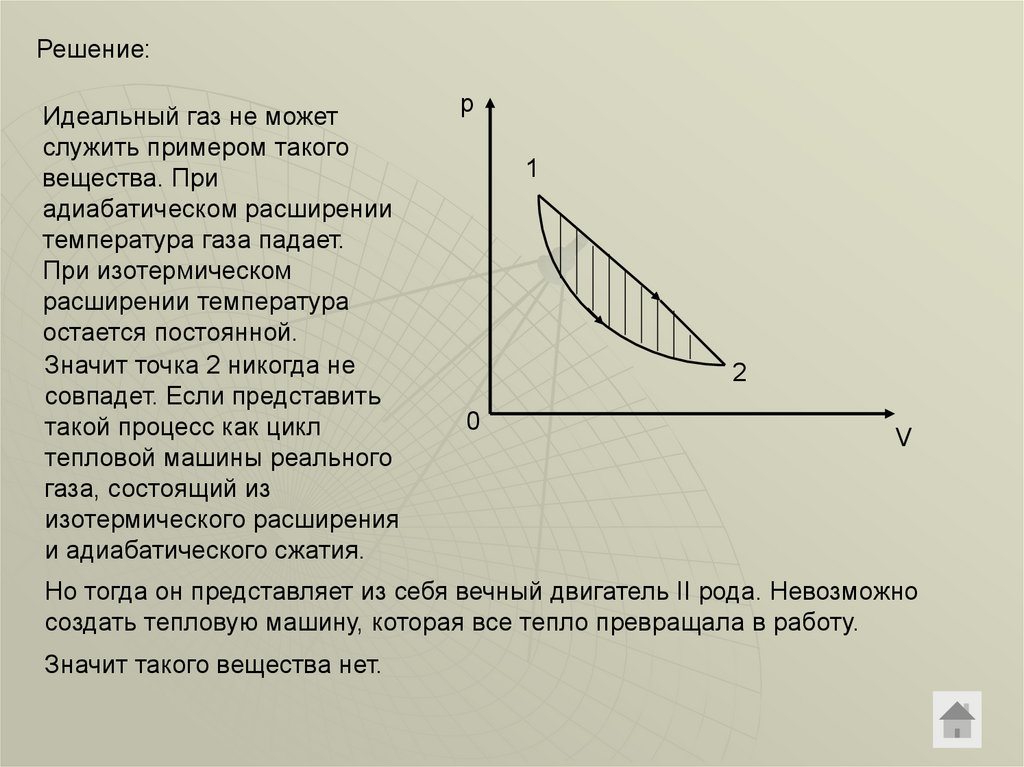
Решение:Идеальный газ не может
служить примером такого
вещества. При
адиабатическом расширении
температура газа падает.
При изотермическом
расширении температура
остается постоянной.
Значит точка 2 никогда не
совпадет. Если представить
такой процесс как цикл
тепловой машины реального
газа, состоящий из
изотермического расширения
и адиабатического сжатия.
p
1
2
0
V
Но тогда он представляет из себя вечный двигатель II рода. Невозможно
создать тепловую машину, которая все тепло превращала в работу.
Значит такого вещества нет.
39.
40.
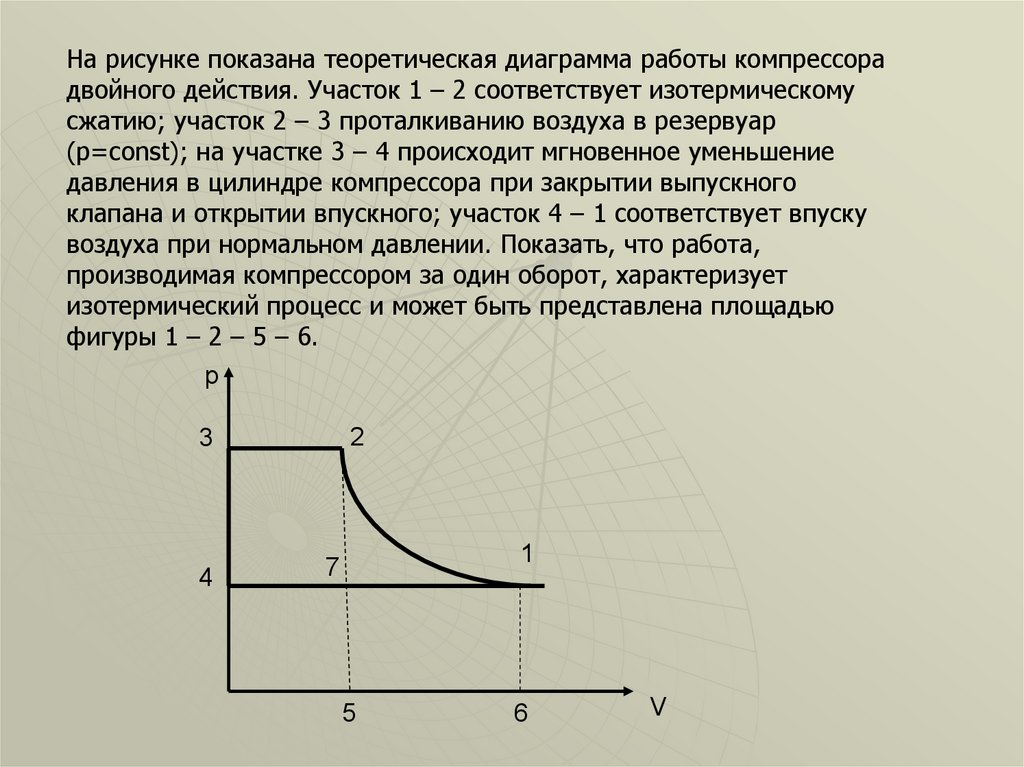
На рисунке показана теоретическая диаграмма работы компрессорадвойного действия. Участок 1 – 2 соответствует изотермическому
сжатию; участок 2 – 3 проталкиванию воздуха в резервуар
(p=const); на участке 3 – 4 происходит мгновенное уменьшение
давления в цилиндре компрессора при закрытии выпускного
клапана и открытии впускного; участок 4 – 1 соответствует впуску
воздуха при нормальном давлении. Показать, что работа,
производимая компрессором за один оборот, характеризует
изотермический процесс и может быть представлена площадью
фигуры 1 – 2 – 5 – 6.
p
2
3
4
1
7
5
6
V
41.
Решение:p
2
3
4
1
7
5
6
V
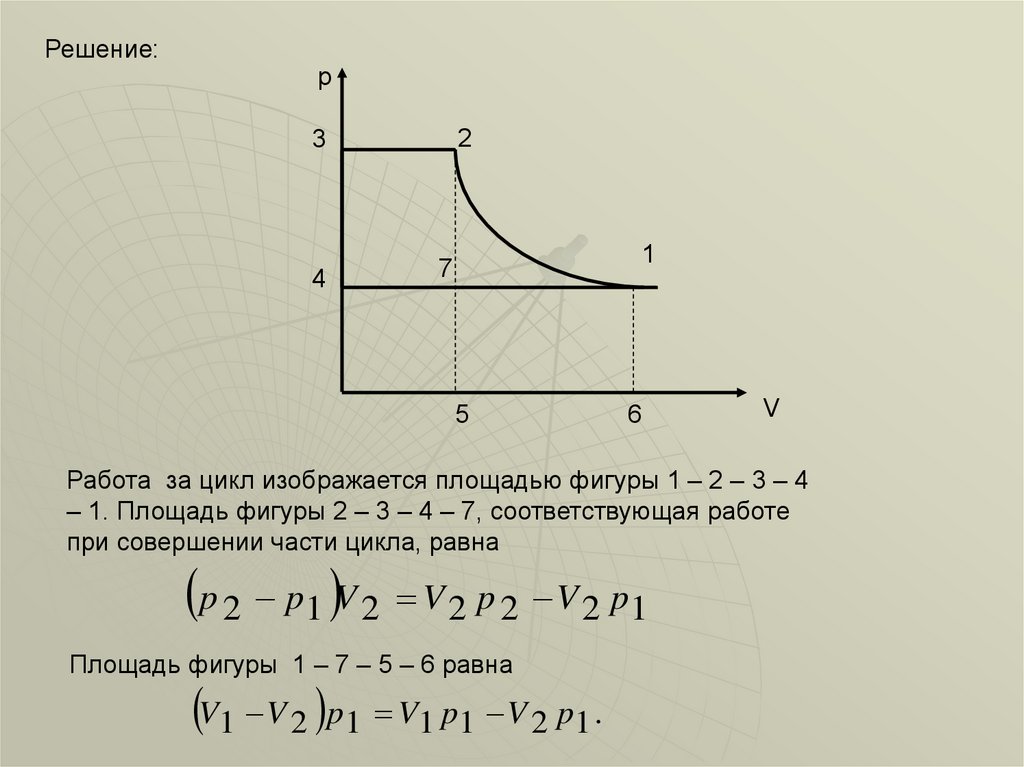
Работа за цикл изображается площадью фигуры 1 – 2 – 3 – 4
– 1. Площадь фигуры 2 – 3 – 4 – 7, соответствующая работе
при совершении части цикла, равна
p 2 p1 V 2 V 2 p 2 V 2 p1
Площадь фигуры 1 – 7 – 5 – 6 равна
V1 V 2 p1 V1 p1 V 2 p1 .
42.
Так как точки 1 и 2 лежат на одной изотерме, тоV 2 p1 V 1 p 1 .
Следовательно,
S 12341 S 1271 S 17561 S 12561,
то есть за один оборот равна работе при изотермическом
процессе.
43.
44.
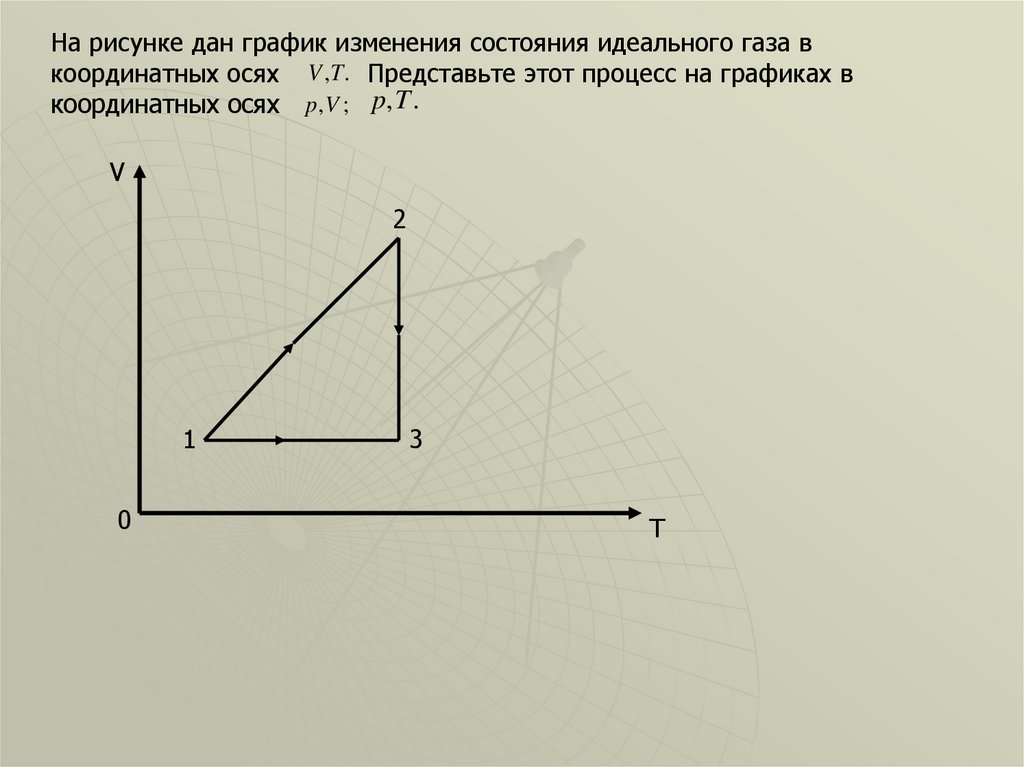
На рисунке дан график изменения состояния идеального газа вкоординатных осях V ,T . Представьте этот процесс на графиках в
координатных осях p ,V ; p,T .
V
2
1
0
3
T
45.
Решение.V
2
1
0
3
T
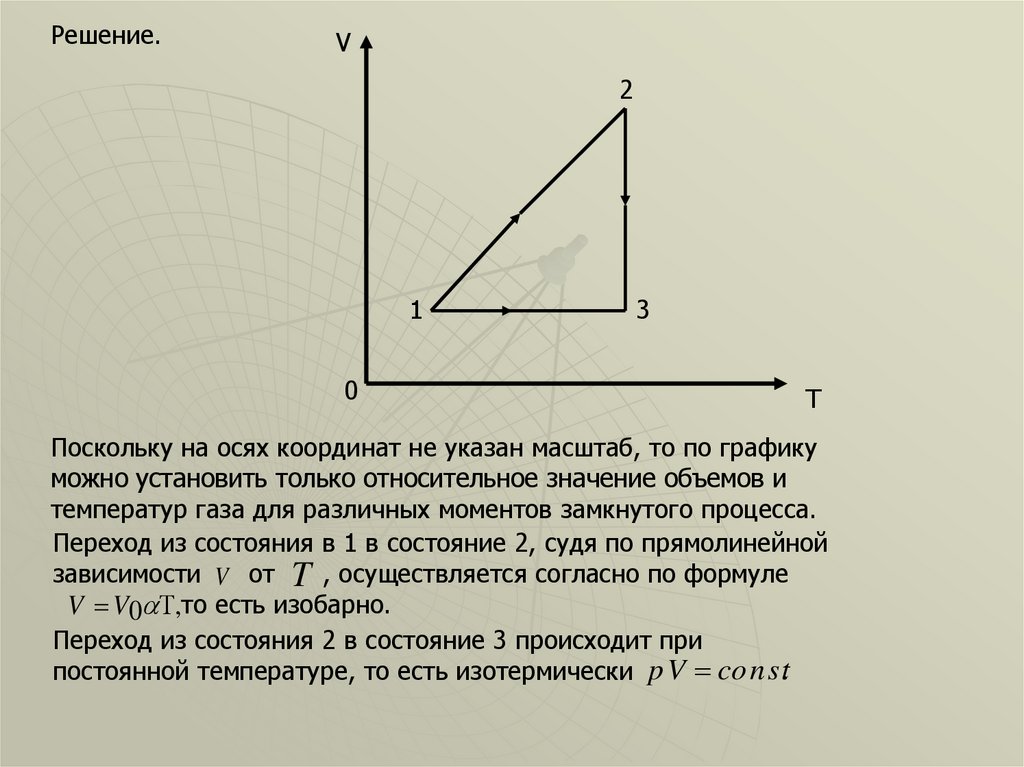
Поскольку на осях координат не указан масштаб, то по графику
можно установить только относительное значение объемов и
температур газа для различных моментов замкнутого процесса.
Переход из состояния в 1 в состояние 2, судя по прямолинейной
зависимости V от T , осуществляется согласно по формуле
V V0 ,то есть изобарно.
Переход из состояния 2 в состояние 3 происходит при
постоянной температуре, то есть изотермически p V co nst.
46.
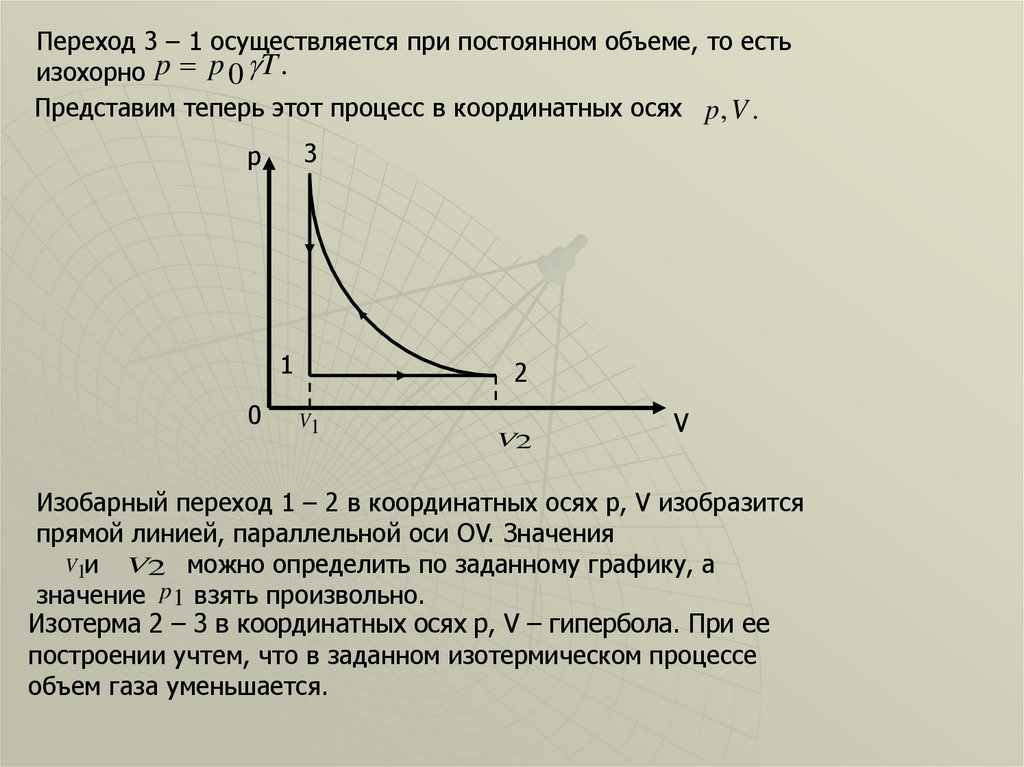
Переход 3 – 1 осуществляется при постоянном объеме, то естьизохорно p p 0 T .
Представим теперь этот процесс в координатных осях p ,V .
3
p
1
0
2
V1
V2
V
Изобарный переход 1 – 2 в координатных осях p, V изобразится
прямой линией, параллельной оси ОV. Значения
V1и V2 можно определить по заданному графику, а
значение p1 взять произвольно.
Изотерма 2 – 3 в координатных осях p, V – гипербола. При ее
построении учтем, что в заданном изотермическом процессе
объем газа уменьшается.
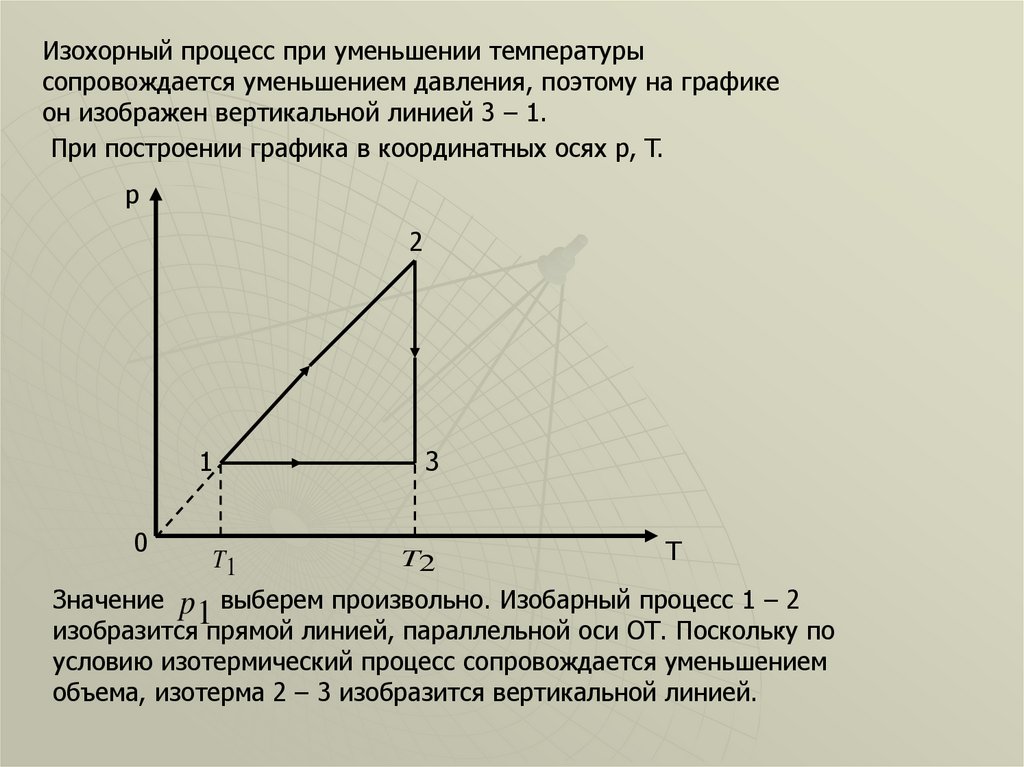
47.
Изохорный процесс при уменьшении температурысопровождается уменьшением давления, поэтому на графике
он изображен вертикальной линией 3 – 1.
При построении графика в координатных осях p, T.
p
2
1
0
T1
3
T2
T
Значение p выберем произвольно. Изобарный процесс 1 – 2
1
изобразится прямой линией, параллельной оси ОТ. Поскольку по
условию изотермический процесс сопровождается уменьшением
объема, изотерма 2 – 3 изобразится вертикальной линией.
48.
Точка 3 должна находиться на изотерме T2 - 2 и наизохоре, часть которой О – 1 изображена пунктиром.
Продолжая прямую О – 1 до пересечения с прямой T2- 2,
найдем точку 3.
После этого ясно, что изохорный процесс изобразится
отрезком 3 – 1.
49.
50.
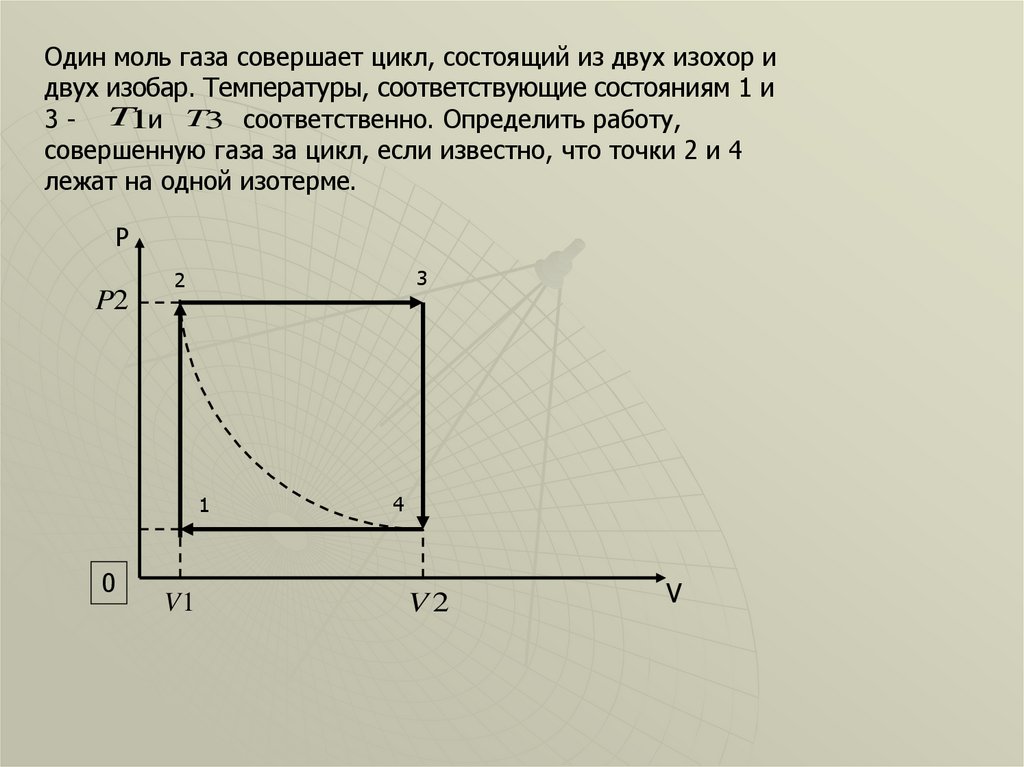
Один моль газа совершает цикл, состоящий из двух изохор идвух изобар. Температуры, соответствующие состояниям 1 и
3 - T1и T3 соответственно. Определить работу,
совершенную газа за цикл, если известно, что точки 2 и 4
лежат на одной изотерме.
P
P2
3
2
1
0
V1
4
V2
V
51.
Дано:T1
T3
Решение:
P
P2
3
2
m
2 4
Найти:
1
А=?
0
4
V1
V2
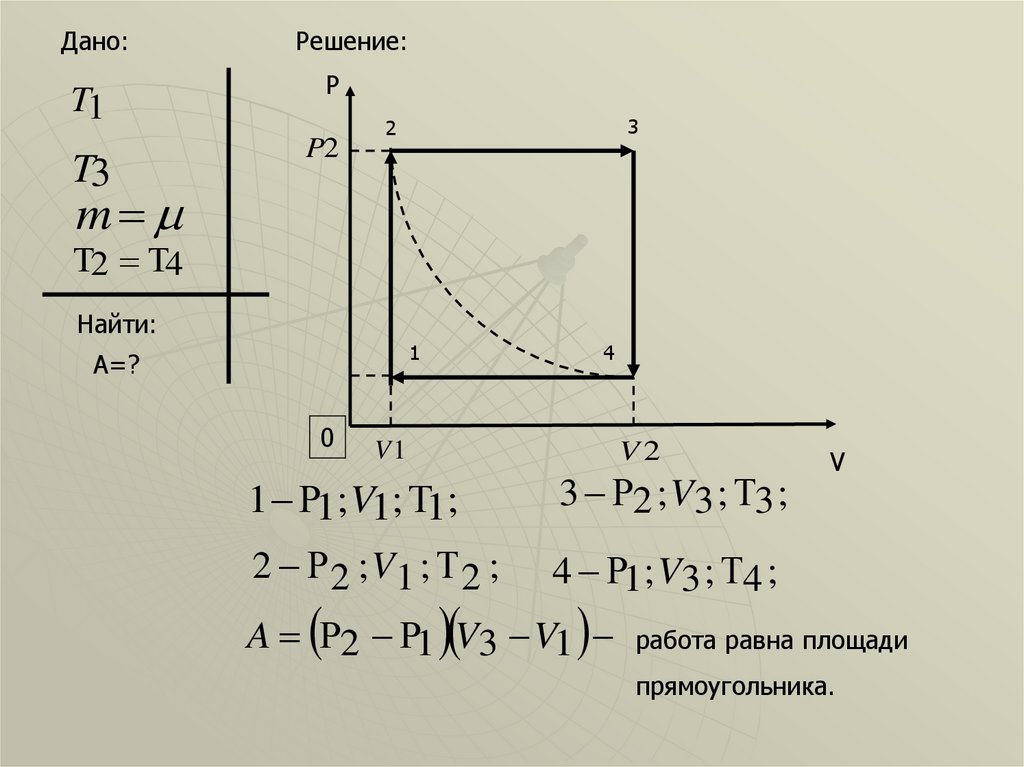
1 1; V1; 1;
3 2 ; V3 ; 3 ;
2 2 ; V1 ; 2 ;
4 1 ; V3 ; 4 ;
A 2 1 V3 V1
V
работа равна площади
прямоугольника.
52.
(1)Так как 2 4 2V1 1V3
Уравнение Клайперона-Менделеева:
1V1
2V3
1
3
Из
m
m
RT1
( так как
m
1 ) 1V1 RT1;
RT3 2 V3 RT3 .
P1
V
T
1 1
P2 V3
T3
(2)
(3)
(4)
V1
P1
V1
1
4
V
P2
V3
3
2
T1
V
1
T3
V3
T1
.
T3
Преобразуем уравнение для работы:
A 2 1 V3 V1 P2V3 P1V3 P2V1 P1V1
P1V1
P1
V1
P2V3 1
P2
V3
P2V3
P2V3 1 P1 1 V1
P
V
2
3
53.
V1RT3 1
V3
Ответ:
2
RT 1 T1
3
T3
2
T1
A RT3 1
.
T3
2
.



















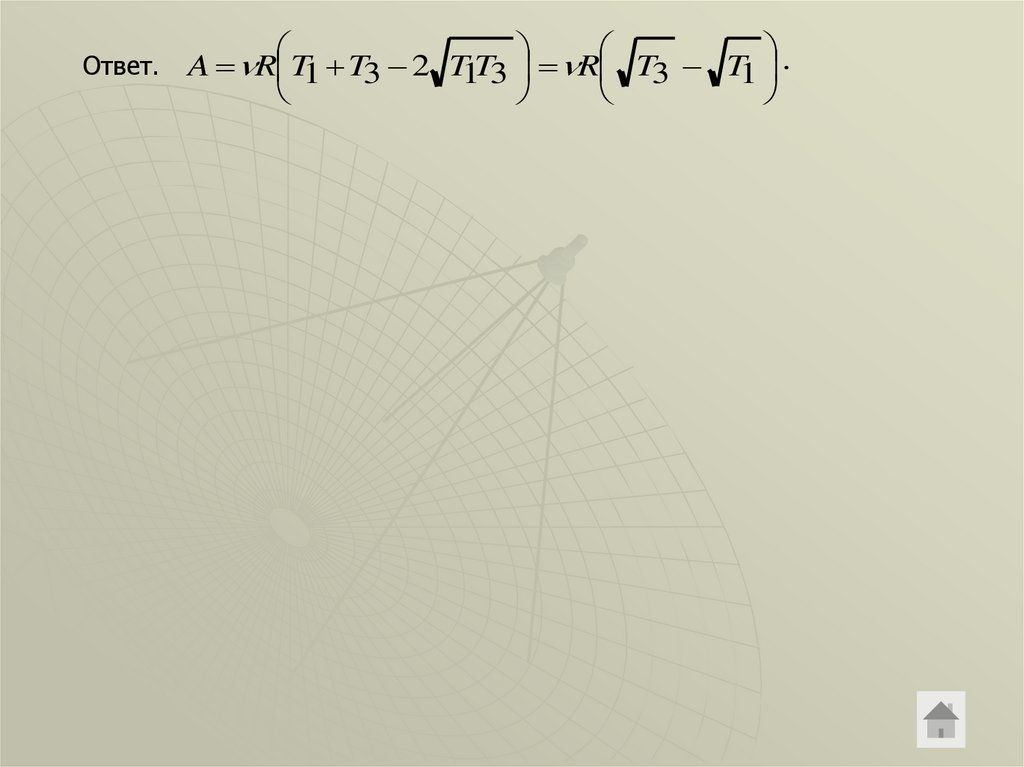






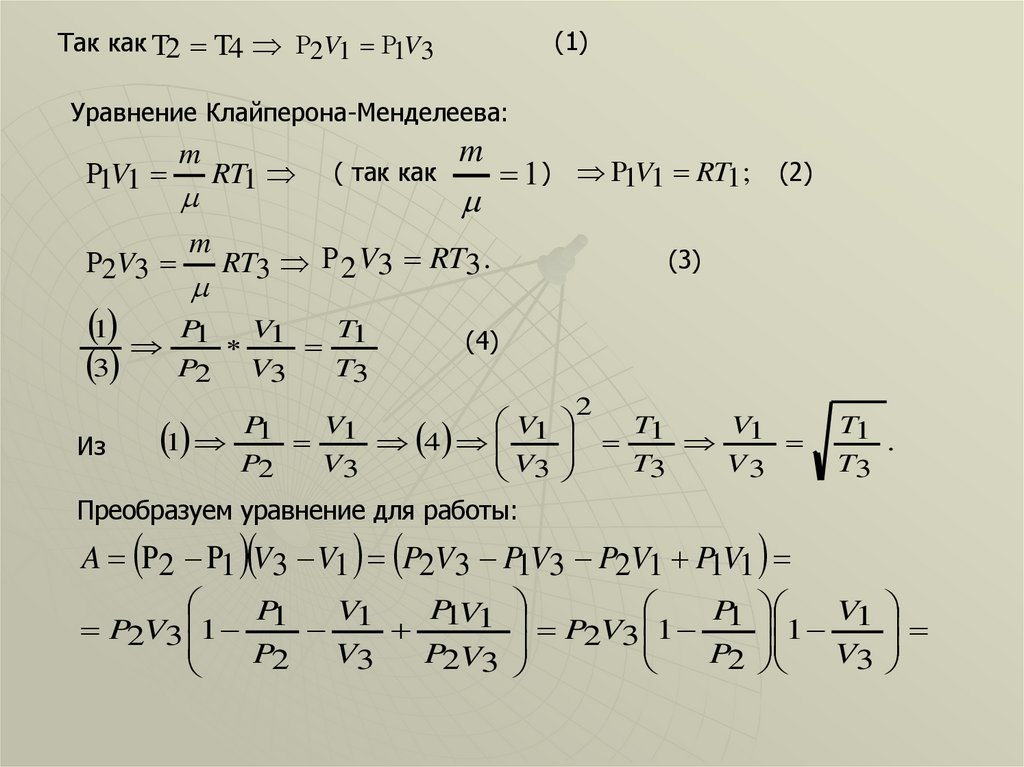
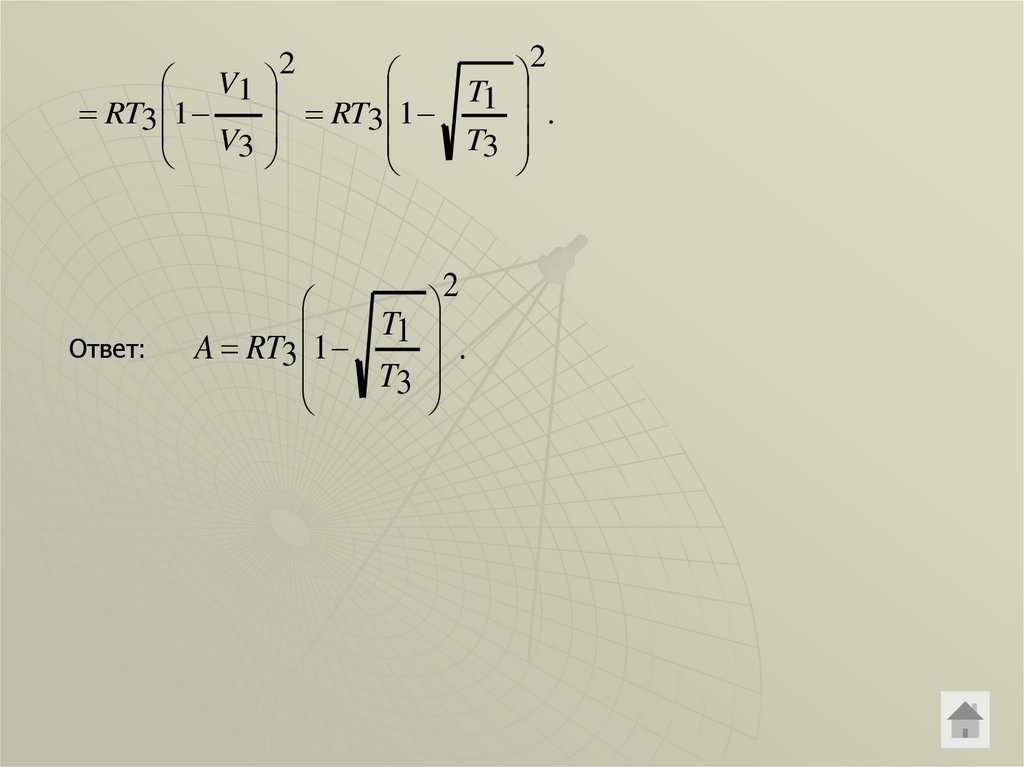
 physics
physics








