Similar presentations:
Применение первого начала термодинамики к изопроцессам
1.
Применение первого начала термодинамики кизопроцессам
Изопроцессом называется процесс, при котором один из
параметров системы остается постоянным.
И зохор а
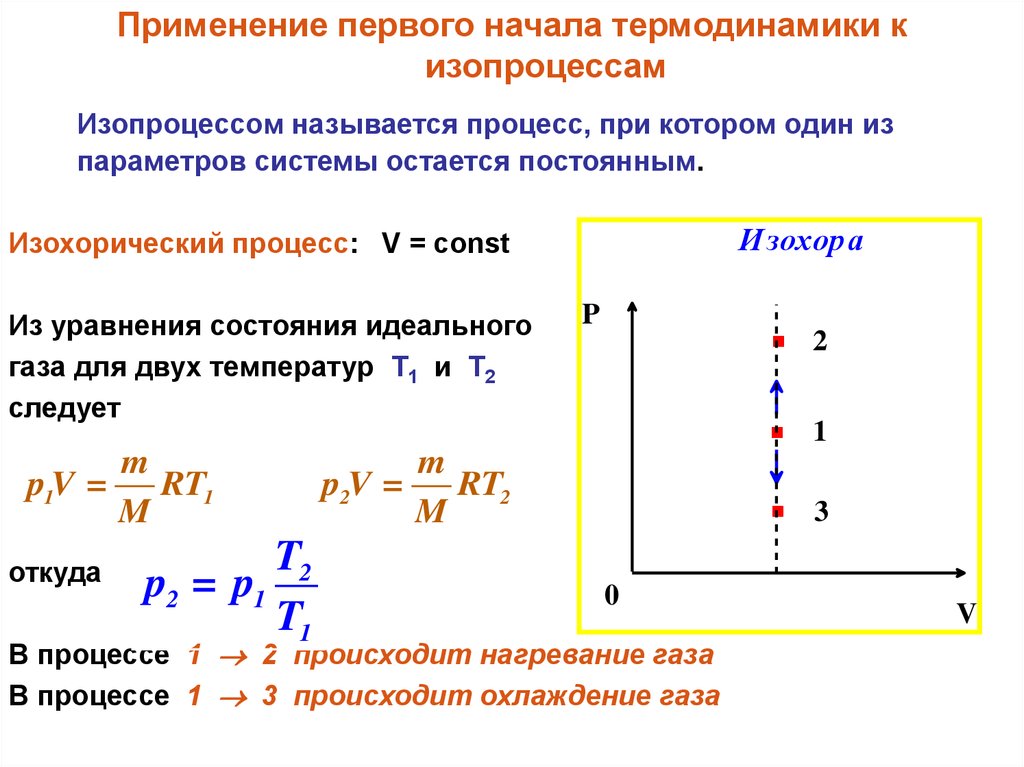
Изохорический процесс: V = const
Из уравнения состояния идеального
газа для двух температур T1 и T2
следует
m
p1V =
RT1
M
откуда
T2
p2 = p1
T1
.
.
.
P
m
p2V =
RT2
M
0
В процессе 1 2 происходит нагревание газа
В процессе 1 3 происходит охлаждение газа
2
1
3
V
2.
Пусть начальное состояние газа отвечает состоянию принормальных условиях Т0 = 0°С = 273.15 °К, р0 = 1 атм, тогда для
произвольной температуры Т давление в изохорическом
процессе находится из уравнения
T
p = p0
T0
Давление газа пропорционально его температуре - Закон Шарля
Поскольку
d A = pdV = 0 , то при изохорическом процессе газ
не совершает работу над внешними телами.
При этом переданная газу теплота равна
d Q = d А + dU = dU
То есть при изохорическом процессе вся теплота, передаваемая
газу, идет на увеличение его внутренней энергии.
В итоге получаем
m
d'Q = dU =
cV dT
M
3.
Изобарический процесс: p = constВ изобарическом процессе газ
совершает работу
И зобар а
P
.
V2
A=
1
pdV = p(V2 -V1 )
.
2
V1
Работа равна площади под прямой
изобары. Из уравнения состояния
идеального газа получаем
m
pV1 =
RT1
M
V
0
V1
m
pV2 =
RT2
M
m
A = p(V2 -V1 ) =
R(T2 T1 )
M
V2
4.
Перепишем последнее соотношение в видеA
R=
ν(T2 - T1 )
Это равенство раскрывает физический смысл газовой постоянной
R - она равна работе 1 моля идеального газа, совершаемой им при
нагревании на 1° К в условиях изобарного расширения.
Возьмем в качестве начального состояния - состояние идеального
газа при нормальных условиях (Т0, V0), тогда объем газа V при
произвольной температуре Т в изобарическом процессе равен
T
V = V0
T0
Объем газа при постоянном давлении пропорционален его
температуре - закон Гей-Люссака.
5.
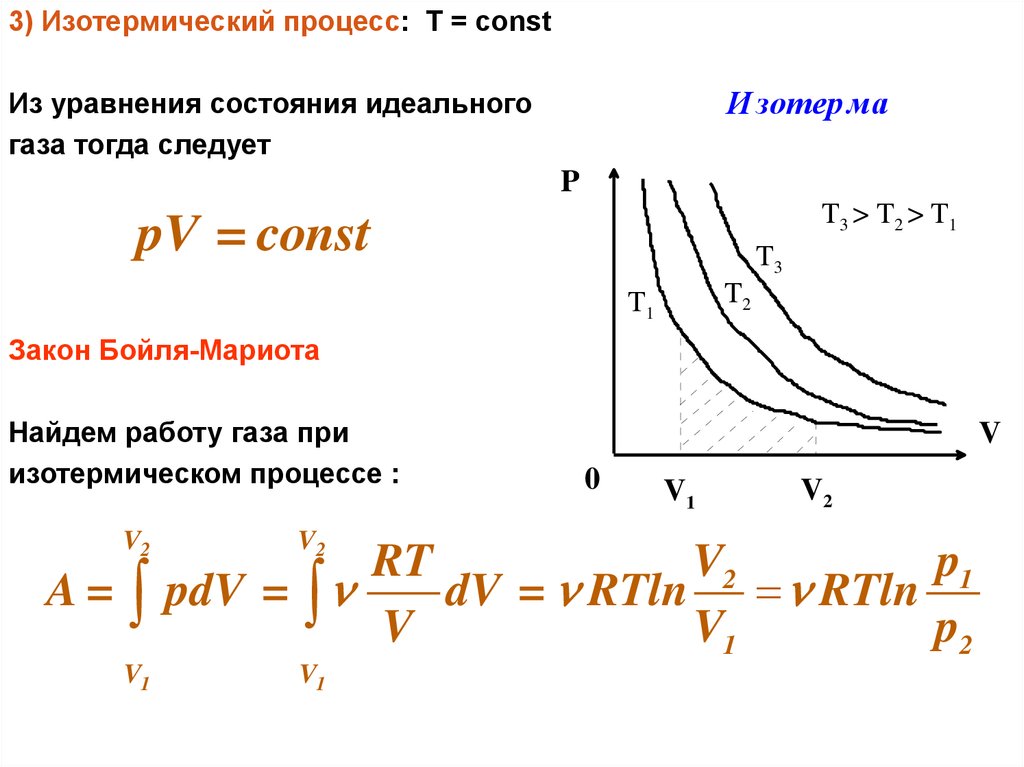
3) Изотермический процесс: Т = constИ зотер ма
Из уравнения состояния идеального
газа тогда следует
P
T3 > T 2 > T 1
pV = const
T3
T2
T1
Закон Бойля-Мариота
Найдем работу газа при
изотермическом процессе :
V2
A=
V1
V2
V
0
V1
V2
RT
V2
p1
pdV =
dV = RTln RTln
V
V1
p2
V1
6.
Используя формулу U = сVT ,получаем
dU = сV dT = 0
Следовательно, внутренняя энергия газа при
изотермическом процессе не меняется .
Поэтому
d'Q = d'A
Значит, при изотермическом процессе вся теплота,
сообщаемая газу, идет на совершение им работы над
внешними телами.
Поэтому
m
p1
Q = A=
RTln
M
p2
Чтобы при расширении газа его температура не
понижалась, к газу необходимо подводить количество
теплоты, равное его работе над внешними телами.
7.
4) Адиабатический процесс : d'Q = 0При адиабатическом процессе теплообмен между газом и
окружающей средой отсутствует. Из первого начала
термодинамики получаем
d'A = - dU
Поэтому в адиабатическом процессе работа газа над
внешними телами совершается за счет убыли его
внутренней энергии.
Используя
dU = сVdT
;
d'A = рdV
находим
рdV = - сV dT
С другой стороны, из уравнения состояния идеального газа
следует
d(рV) = pdV + Vdp = RdT
8.
ИсключаяdT , получаем
рdV = - сV (pdV + vdp)/R
Откуда
dp
R dV
dV
= -( 1 + )
= -γ
p
cV V
V
Интегрируя, находим
p2
V2
dp
dV
p p = -γ V V
1
1
p2
V2
ln( ) = -γln( )
p1
V1
9.
Последнюю формулу можно переписать в видеγ
p2 V1
=
p1 V2
γ
1 1
γ
2
p V = p2V
Следовательно
Адиабата
P
γ
pV = const
это уравнение адиабатического процесса
- уравнение Пуассона
V1
Так как > 1 , то у адиабаты давление 0
меняется от объема быстрее, чем у изотермы.
И зотер ма
V2
V
10.
Используя уравнение состояния идеального газа,преобразуем уравнение Пуассона к виду
pV = νRT
Значит
или
TV
p
(γ -1)
(1-γ)
νRTV (γ -1) = const
= const
γ
T = const
При адиабатическом расширении идеальный газ
охлаждается, а при сжатии – нагревается.
11.
Найдем работу газа при адиабатическом процессе.Из первого начала термодинамики
d'A = - cV dT
после интегрирования, находим
A = -νcV (T2 - T1 )
Выразим работу газа через давление и объем. Для этого
преобразуем формулу к виду
T1 V2
=
T2 V1
(γ -1)
12.
ТогдаИспользуя
получаем
V1
A = νcV T1[1 -
V2
R
cV
-1
и
( -1)
]
p1V1 = RT1
V1
p1V1
A=
[1 -
γ -1
V2
( -1)
]
13.
11.6 Политропические процессыПолитропический процесс – это процесс в ходе которого
теплоемкость газа остается постоянной:
cm = const
где cm – молярная теплоемкость.
Найдем уравнение политропы для идеального газа.
Из первого начала термодинамики следует
d'Q = dU + pdV = νcm dT
dU = νdU m = νcV dT
откуда получаем
ν(cm - cV )dT = pdV
14.
С другой стороны, из уравнения состояния идеального газаd(pV) = d(νRT) pdV +Vdp = νRdT
Поэтому можно записать
(cm - cV )(pdV + VdP) = pRdV
(cm - cV - R)pdV + (cm - cV )Vdp = 0
Поскольку
cP = cV + R
то
dV
dp
(cm - c P )
+ (cm - cV ) = 0
V
p
15.
cm - c Pn=
cm - cV
Обозначим
Интегрируем
, получим
V2
p1
nln = ln
V1
p2
Следовательно
dV dp
n
+
=0
V
p
p2V2n = p1V1n
n
pV = const
Это - уравнение политропы,
n - показатель политропы.
Все предыдущие процессы являются частными случаями
политропического процесса:
n = 0 изобара
cm = cP
n = 1 изотерма cm =
n = изохора
cm = cV
n = адиабата cm = 0
16.
Изменение энтропии в неадиабатических процессахидеального газа
В неадиабатических процессах между
идеальным газом и внешними телами происходит
обмен теплотой. Эти процессы являются
обратимыми, поэтому для их описания можно
использовать формулу, связывающую теплоту и
энтропию. Для малого участка процесса теплота,
переданная газу внешними телами, равна
d'Q = TdS
С другой стороны, согласно первому началу
термодинамики, эту теплоту можно представить в
виде
dV
d'Q = dU + pdV = νcV dT + νRT
V
17.
Поэтому изменение энтропии на конечном участке процессамежду состояниями 1 и 2 равно интегралу
2
2
2
dV
dT
d'Q
νR
= νcV
S =
V
T 1
T
1
1
V2
T2
= νcV ln( ) + νRln( )
V1
T1
18.
Отсюда следует, что1 ) при изотермическом процессе ( Т2 = Т1 )
V2
S = νRln( )
V1
2 ) при изохорическом процессе ( V2 = V1 )
T2
S = νcV ln( )
T1
3 ) при изобарическом процессе ( p2 = p1 ,
V1 T1
V2 T2
)
V2
V2
T2
S = ν(cV + R)ln( ) = νc P ln( ) = νc P ln( )
V1
V1
T1
19.
Изменение энтропии при плавлении и испаренииЕсли при плавлении или испарении давление не меняется,
то как показывает опыт, в таких процессах у большинства
веществ температура тоже остается постоянной. Поэтому
изменение удельной энтропии (для единицы массы вещества)
в ходе плавления равно
жидк
Δsпл =
тв
d'Q
1
=
Tпл Tпл
жидк
тв
qпл
d'Q =
Tпл
где qпл – удельная теплота плавления.
20.
Аналогично, изменение удельной энтропии в ходе кипения(испарения) равно
газ
Δsкип =
жидк
где
d'Q
1
=
Tкип Tкип
газ
жидк
qкип
d'Q =
Tкип
qкип – удельная теплота кипения.
21. В сосуде под поршнем находится масса m=1г азота. Какое количество теплоты Q надо затратить, чтобы нагреть азот на ΔТ=10К? На сколько при этом по
В сосуде под поршнем находится масса m=1г азота. Какоеколичество теплоты Q надо затратить, чтобы нагреть азот
на ΔТ=10К? На сколько при этом поднимется поршень? Масса
поршня М=1 кг, площадь его поперечного сечения S=10 см2.
Давление под поршнем p=100 кПа.
Согласно первому началу термодинамики
Q=ΔU+A
Тогда Q =
i m
ΔU =
RΔT
2μ
5m
m
7m
RΔT + RΔT
RΔT
2μ
μ
2μ
i=5
A = RΔT =
m
RΔT
μ
Q=10.39 Дж.
При расширении газ совершает работу против сил тяжести и против
сил атмосферного давления, тогда
A = Mg pS Δh =
m
mRΔT
RΔT Δh
μ
μ Mg pS
Δh=2.7 см.



















 physics
physics








