Similar presentations:
Применение интеграла к вычислению площадей
1.
И5Практическая работа №32 (1):
Применение интеграла к
вычислению площадей.
2.
1. Вычислите:3 2 3 11 11
3 11
7 33
7 33
2
14 2 33
2 7 33
7 33
7 33
2
3.
Повторение:3
2
1 t
dt
t
x
4
5
x
dx
0
20 3
20
2
1
4
3
4 5x t
4 2
1 4 5 x
3
20 x dx dt
10
3
dt
0
3
x dx
3
3
20
19
27 8
92 42
30 30 30 30 30
1
3
4
4.
Повторение:4
dt
1
t
t
5
2
x
dx
2
2
2 4
1
3
5 2x t
2 dx dt
dt
dx
2
3
5 2x
4 1
8
2
81 6561
810
8
8
5.
Площадь плоской фигурыГеометрический смысл определённого интеграла заключается в
нахождении площади криволинейной трапеции по формуле
Ньютона-Лейбница:
b
b
a
a
S f ( x)dx F ( x) F (b) F (a )
6.
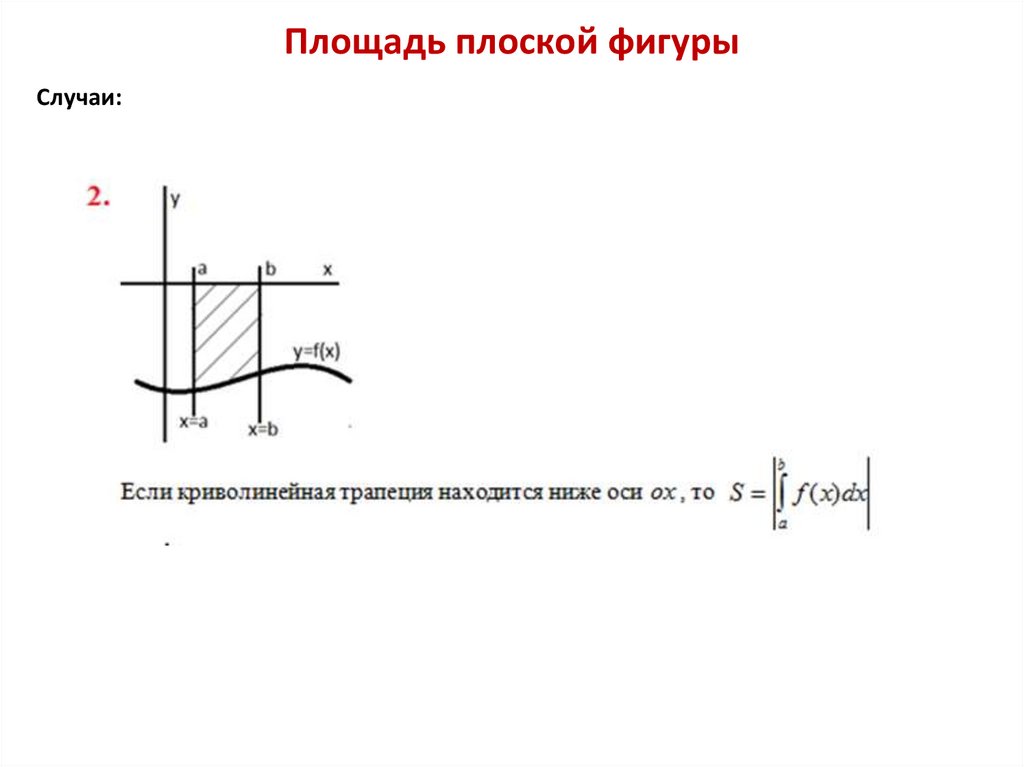
Площадь плоской фигурыСлучаи:
7.
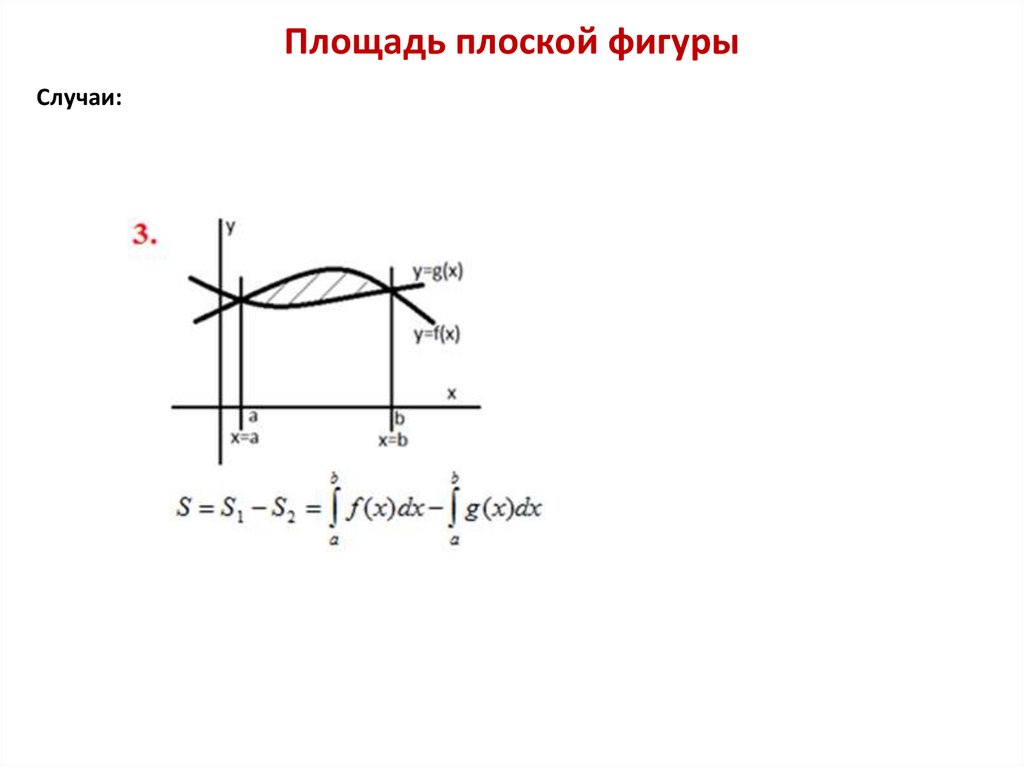
Площадь плоской фигурыСлучаи:
8.
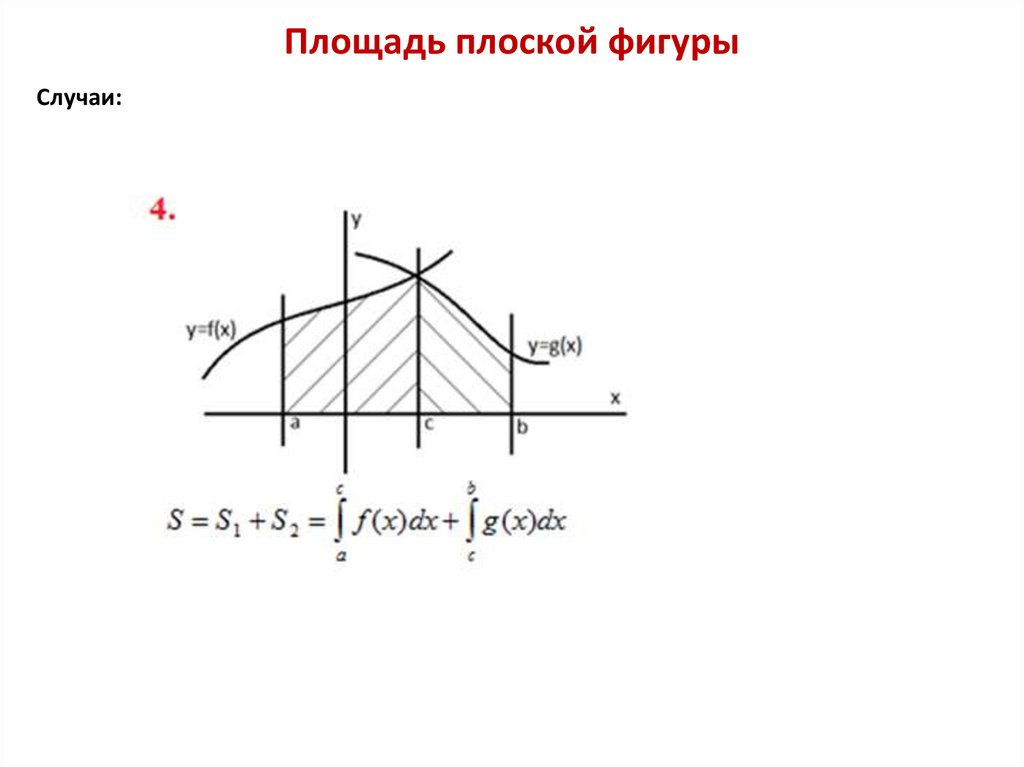
Площадь плоской фигурыСлучаи:
9.
Площадь плоской фигурыСлучаи:
10.
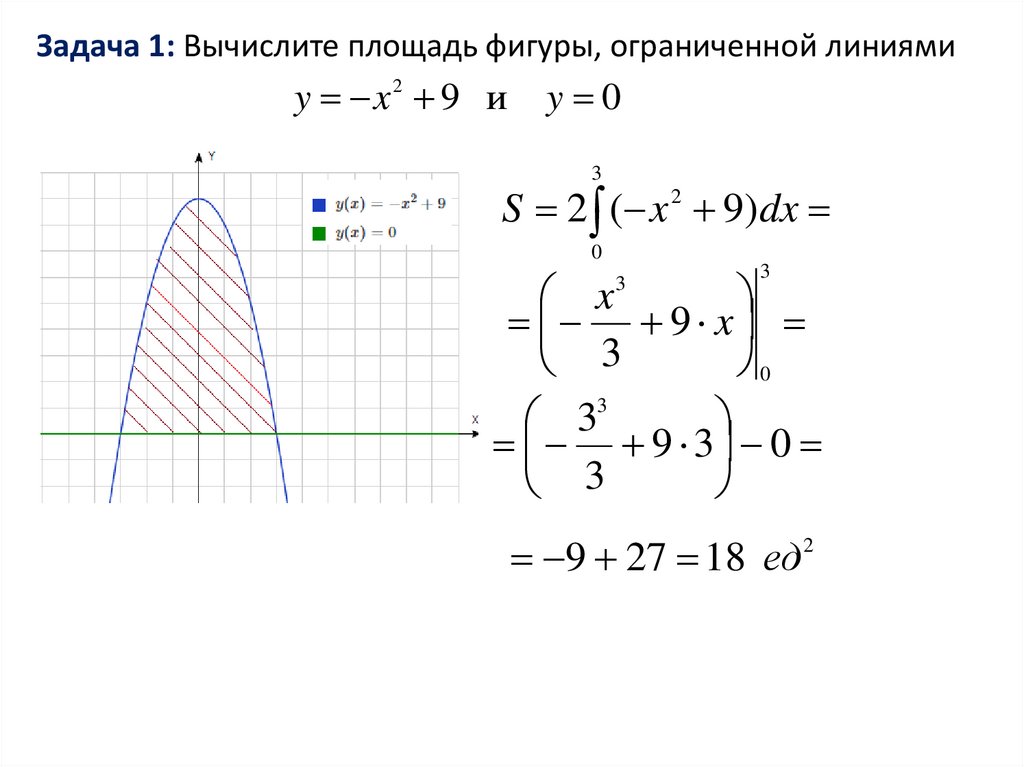
Задача 1: Вычислите площадь фигуры, ограниченной линиямиy x2 9 и
y 0
3
S 2 ( x 9)dx
2
0
3
x
9 x
3
0
33
9 3 0
3
3
9 27 18 ед
2
11.
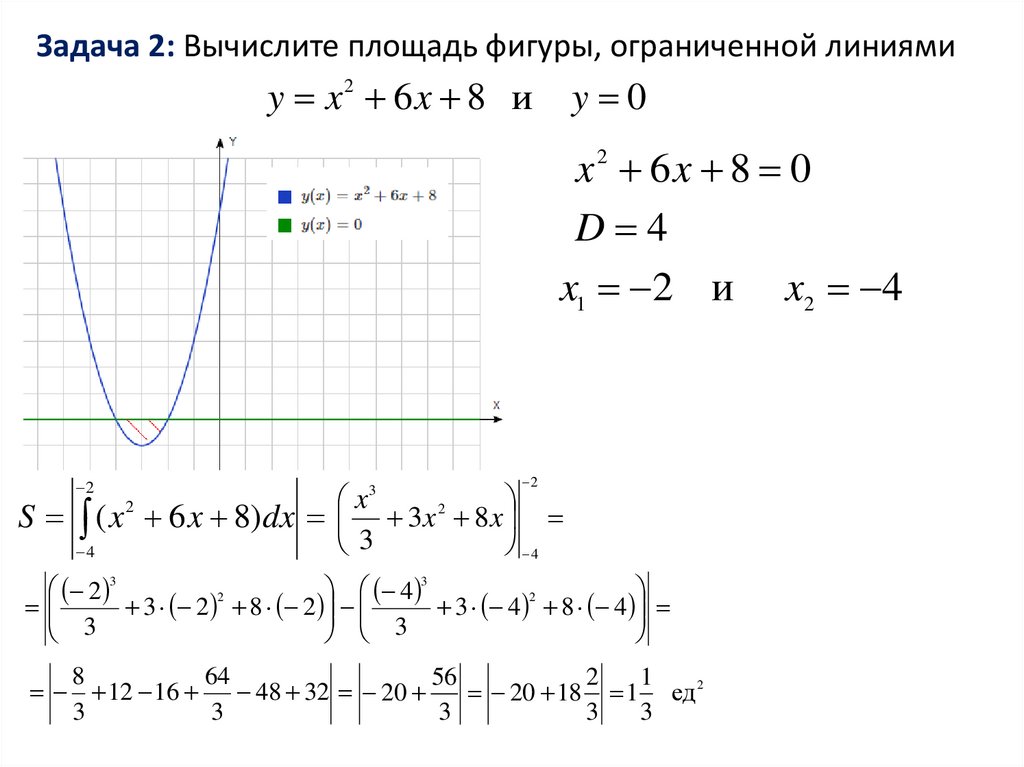
Задача 2: Вычислите площадь фигуры, ограниченной линиямиy x2 6x 8 и
y 0
x 6x 8 0
D 4
x1 2 и x2 4
2
2
4
2
x
3x 2 8 x
3
4
S ( x 2 6 x 8)dx
3
2 3
4 3
2
2
3 2 8 2
3 4 8 4
3
3
8
64
56
2
1
12 16
48 32 20
20 18 1 ед 2
3
3
3
3
3
12.
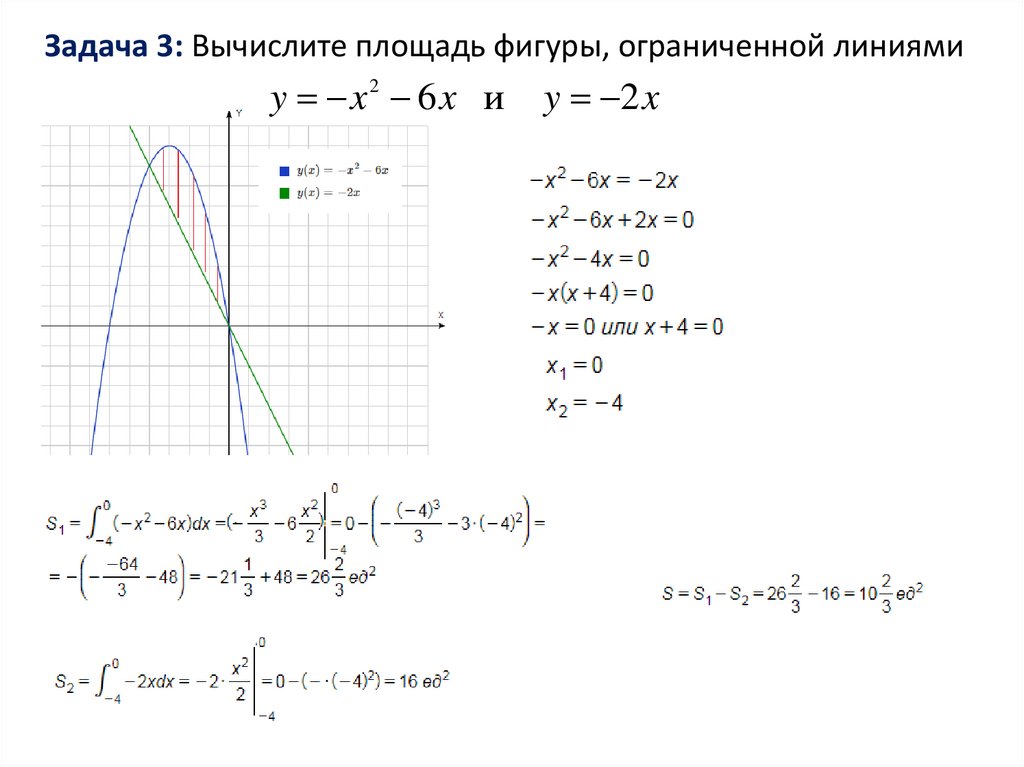
Задача 3: Вычислите площадь фигуры, ограниченной линиямиy x2 6x и
y 2 x
13.
Задача 4: Вычислите площадь фигуры, ограниченной линиямиy x2 4x 4 и
y 2x 4
14.
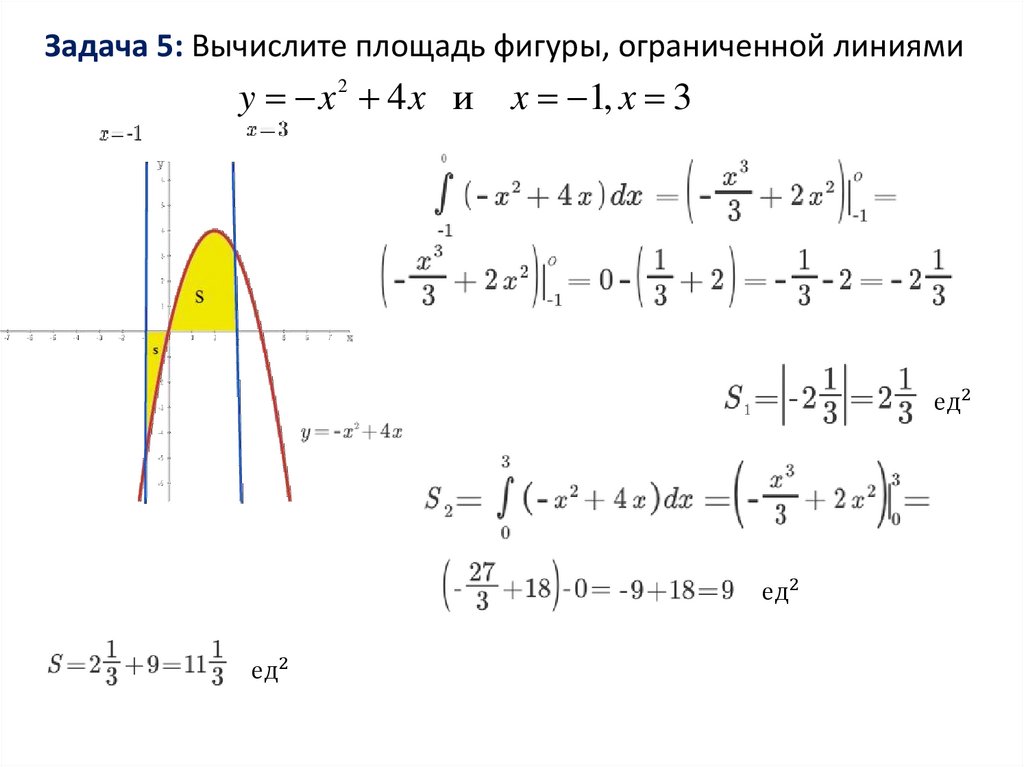
Задача 5: Вычислите площадь фигуры, ограниченной линиямиy x2 4x и
x 1, x 3
ед2
ед2
ед2
15.
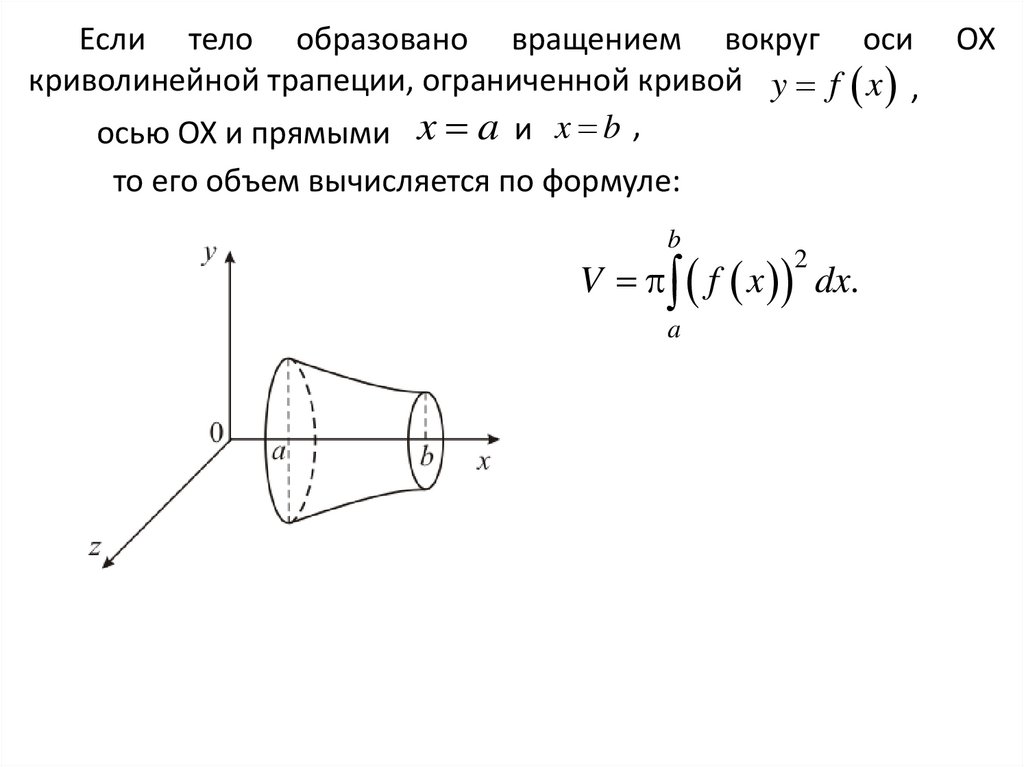
Если тело образовано вращением вокруг осикриволинейной трапеции, ограниченной кривой y f x ,
осью OX и прямыми x a и x b ,
то его объем вычисляется по формуле:
b
V f x dx.
a
2
OX







 mathematics
mathematics








