Similar presentations:
Прием рациональных вычислений
1.
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ЛИЦЕЙ №22 ГОРОДА БЕЛОВОПрием рациональных
вычислений
Выполнил: Филиппов Вадим,
ученик 7 «Б» класса
Руководитель: Шумилова С.Н.,
учитель математики
2.
ЦЕЛИ И ЗАДАЧИЦель: Изучить приемы рациональных
вычислений, и показать что их применение
делает вычисления полезными, интересными и
быстрыми.
Задачи:
• Научиться применять приемы рациональных вычислений
• Выбрать для себя самые интересные или более легкие
приемы, и использовать их при счете
• Проверить себя в программе LearningApps.org
3.
АКТУАЛЬНОСТЬ ТЕМЫЧеловеку в повседневной жизни невозможно
обойтись без вычислений. Поэтому на уроках
математики, нас в первую очередь учат
выполнять действия над числами, то есть
считать. Умножаем, делим, складываем и
вычитаем мы привычными для всех
способами, которые изучаются в школе. Но
так же кроме привычных для нас приемов и
способов, есть и другие приемы
рациональных вычислений, о которых и
пойдет речь.
4.
ПРИМЕНЕНИЕПрименение в первую очередь конечно же
на уроках, но и даже в повседневной жизни
это приемы рациональных вычислений
пригодятся.
5.
ЧТО ТАКОЕ LEARNINGAPPS.ORG?LearningApps.org является приложением Web 2.0 для
поддержки обучения и процесса преподавания с
помощью интерактивных модулей. Существующие
модули могут быть непосредственно включены в
содержание обучения, а также их можно изменять или
создавать в оперативном режиме. Целью является
также собрание интерактивных блоков и возможность
сделать их общедоступным. Такие блоки (так
называемые приложения или упражнения ) не
включены по этой причине ни в какие программы или
конкретные сценарии. Они имеют свою ценнность, а
именно - интерактивность.
6.
ПРИЕМЫ УПРОЩЕННОГО УМНОЖЕНИЯ ЧИСЕЛСокращенные приемы умножения на
2,5; 25 и 250
Сокращенные приемы умножения
на 0,15
Сокращенные приемы умножения на
1,25; 12,5; 125
7.
СОКРАЩЕННЫЕ ПРИЕМЫ УМНОЖЕНИЯ НА 2,5;25 И 250
Чтобы умножить число на 2,5; 25; 250, его
необходимо вначале умножить соответственно на
10; 100; 1 000 и разделить на 4.
Пример. Найдем произведение чисел 28 и 250.
Решение. 28 х 250 = (28 х 1 000) / 4 = 28000 / 4 = 7
000.
8.
СОКРАЩЕННЫЕ ПРИЕМЫ УМНОЖЕНИЯ НА0,15
Чтобы умножить число на 0,15, нужно это число
разделить на 10, полученное частное разделить
на 2, а затем оба частных сложить.
Пример. Найдем произведение чисел 240 и 0,15.
Решение. 240 x 0,15 = (240 / 10) + 1/2 х (240 / 10)
= 24 + 12 = 36.
9.
СОКРАЩЕННЫЕ ПРИЕМЫ УМНОЖЕНИЯ НА 1,25;12,5; 125
Чтобы умножить какое-то число на 1,25; 12,5; 125,
его нужно сначала умножить соответственно на
10; 100; 1 000, а затем полученное произведение
разделить на 8.
Пример. Найдем произведение чисел 70 и 12,5.
Решение. 70 х 12,5 = (70 х 100) / 8 = 7 000 / 8 =
875
10.
ПРИЕМЫ УПРОЩЕННОГО ДЕЛЕНИЯ ЧИСЕЛРазложение делимого на слагаемые
Деление на 2,5 и 25
Деление на 1,25 и 12,5
11.
РАЗЛОЖЕНИЕ ДЕЛИМОГО НА СЛАГАЕМЫЕРазложение делимого на такие слагаемые,
которые легко бы делились раздельно,
ускоряет устный подсчет числа при делении.
Пример. Найдем частное чисел 2 808 и 9.
Решение. 2808 / 9 = (2700 / 9) + (90 / 9) + (18 /
9) = 300 + 10 + 2 = 312.
12.
ДЕЛЕНИЕ НА 2,5 И 25Чтобы разделить число на 2,5 или 25,
необходимо разделить его на 10 или 100 и
затем частное умножить на 4.
Пример. Разделим число 285 на 2,5.
Решение. 285 / 2,5 = (285 / 10) х 4 = 28,5 x
4 = 114
13.
ДЕЛЕНИЕ НА 1,25 И 12,5Чтобы разделить число на 1,25 или 12,5,
необходимо разделить его на 10 или 100
и затем частное умножить на 8.
Пример. Разделим число 300 на 12,5.
Решение. 300 / 12,5 = (300 / 100) х 8 = 3 x
8 = 24.
14.
ПРИЕМЫ УПРОЩЕННОГО СЛОЖЕНИЯ ЧИСЕЛСпособ круглого числа
Способ группировки слагаемых
Способ последовательного поразрядного сложения
15.
СПОСОБ КРУГЛОГО ЧИСЛАЧисло, имеющее одну значащую цифру и оканчивающееся одним или
несколькими нулями, называется круглым числом. Этот способ применяется,
когда из двух или более слагаемых можно выбрать такие, которые можно
дополнить до круглого числа. Разность между круглым и заданным в условии
вычислений числами называется дополнением. Например, 1 000 — 978 = 22. В
этом случае число 22 является арифметическим дополнением числа 978 до 1
000.
Чтобы произвести сложение способом круглого числа, необходимо одно или
несколько слагаемых, близких к круглым числам, округлить, выполнить
сложение круглых чисел и из полученной суммы вычесть арифметические
дополнения.
Пример. Найдем сумму чисел 1 238 и 193, используя способ круглого числа.
Решение. Округлим число 193 до 200 и произведем сложение следующим
образом: 1 238 + 193 = (1 238 + 200) - 7 = 1 431.
16.
СПОСОБ ГРУППИРОВКИ СЛАГАЕМЫХЭтот способ применяют в том случае,
когда слагаемые при их группировке в
сумме дают круглые числа, которые затем
складывают между собой.
Пример. Найдем сумму чисел 74, 32, 67,
48, 33 и 26.
Решение. Суммируем числа,
сгруппированные следующим образом:
(74 + 26) + (32 + 48) + (67 + 33) = 280.
17.
СПОСОБ ПОСЛЕДОВАТЕЛЬНОГО ПОРАЗРЯДНОГОСЛОЖЕНИЯ
Используется при устных вычислениях, так как он упрощает и
ускоряет суммирование слагаемых. При использовании этого
способа сложение начинается с высших разрядов: к первому
слагаемому прибавляются соответствующие разряды второго
слагаемого.
Пример. Найдем сумму чисел 5287 и 3564, используя способ
последовательного поразрядного сложения.
Решение. Расчет произведем в такой последовательности:
5 287 + 3 000 = 8 287;
8 287 + 500 = 8 787;
8 787 + 60 = 8 847;
8 847 + 4 = 8 851.
Ответ: 8 851.
18.
ПРИЕМЫ УПРОЩЕННОГО ВЫЧИТАНИЯ ЧИСЕЛСпособ замены вычитания сложением
Способ круглого числа
Способ последовательного поразрядного
вычитания
19.
СПОСОБ ЗАМЕНЫ ВЫЧИТАНИЯ СЛОЖЕНИЕМСпособ заключается в том, что к вычитаемому нужно подобрать такое
число, которое в сумме с ним было бы равно уменьшаемому. Подбор
нужного числа выполняется по частям.
Пример. Найдем разность денежных сумм 50 р. и 28 р. 57 к., используя
способ замены вычитания сложением.
Решение. Для суммы 28 р. 57 к. подберем числа по частям, для чего:
1.добавим к заданной сумме 43 к. и получим 29 р.;
2.добавим к определенной в п. 1 сумме 21 р. для получения суммы 50 р.
Таким образом, искомое число — это результат вычисления слагаемых из
двух сумм, т.е. разность денежных сумм 50 р. и 28 р. 57 к. составляет 21 р.
43 к.
20.
СПОСОБ КРУГЛОГО ЧИСЛАЭтот способ применяют, когда вычитаемое
близко к круглому числу. Для расчета
необходимо из уменьшаемого вычесть
вычитаемое, взятое круглым числом, и к
полученной разности прибавить
арифметическое дополнение.
Пример. Вычислим разность чисел 235 и
197, используя способ круглого числа.
Решение. 235 — 197 = 235 — 200 + 3 = 38.
21.
СПОСОБ ПОСЛЕДОВАТЕЛЬНОГО ПОРАЗРЯДНОГОВЫЧИТАНИЯ
Этим способом производится последовательное вычитание каждого
разряда, вычитаемого из уменьшаемого. Он применяется, когда числа
нельзя округлить.
Пример. Найдем разность чисел 721 и 398.
Решение. Выполним действия для нахождения разности заданных чисел в
следующей последовательности:
1.Представим число 398 в виде суммы: 300 + 90 + 8 = 398;
2.Выполним поразрядное вычитание: 721 — 300 = 421; 421 — 90 = 331; 331
— 8 = 323
22.
НАГЛЯДНЫЙ ПРИМЕР РАЦИОНАЛЬНЫХВЫЧИСЛЕНИЙ С ПОМОЩЬЮ РУК
Раздвиньте пальцы на обеих руках и поверните руки
ладонями от себя. Мысленно присвойте пальцам
последовательно числа от 1 до 10, начиная с мизинца
левой руки и заканчивая мизинцем правой руки (это
изображено на рисунке)
23.
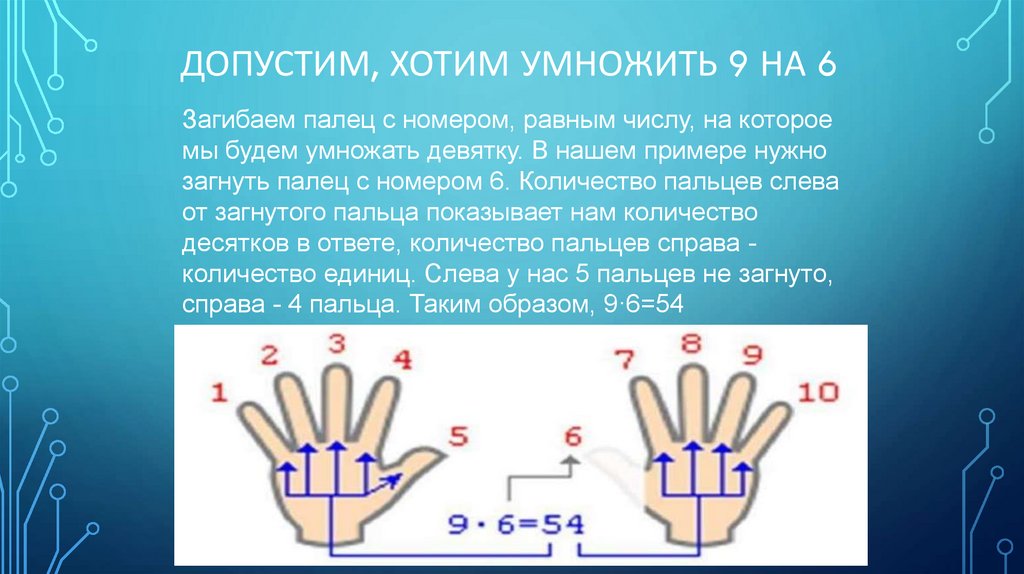
ДОПУСТИМ, ХОТИМ УМНОЖИТЬ 9 НА 6Загибаем палец с номером, равным числу, на которое
мы будем умножать девятку. В нашем примере нужно
загнуть палец с номером 6. Количество пальцев слева
от загнутого пальца показывает нам количество
десятков в ответе, количество пальцев справа количество единиц. Слева у нас 5 пальцев не загнуто,
справа - 4 пальца. Таким образом, 9·6=54
24.
ВЫВОДПрименение рациональных приемов делает
процесс вычисления рациональным, полезным
и интересным.
























 mathematics
mathematics








