Similar presentations:
Действия над рациональными числами
1. Действия над рациональными числами
2. Содержание
Сложение рациональных чисел.
Вычитание рациональных чисел.
Умножение рациональных чисел.
Деление рациональных чисел.
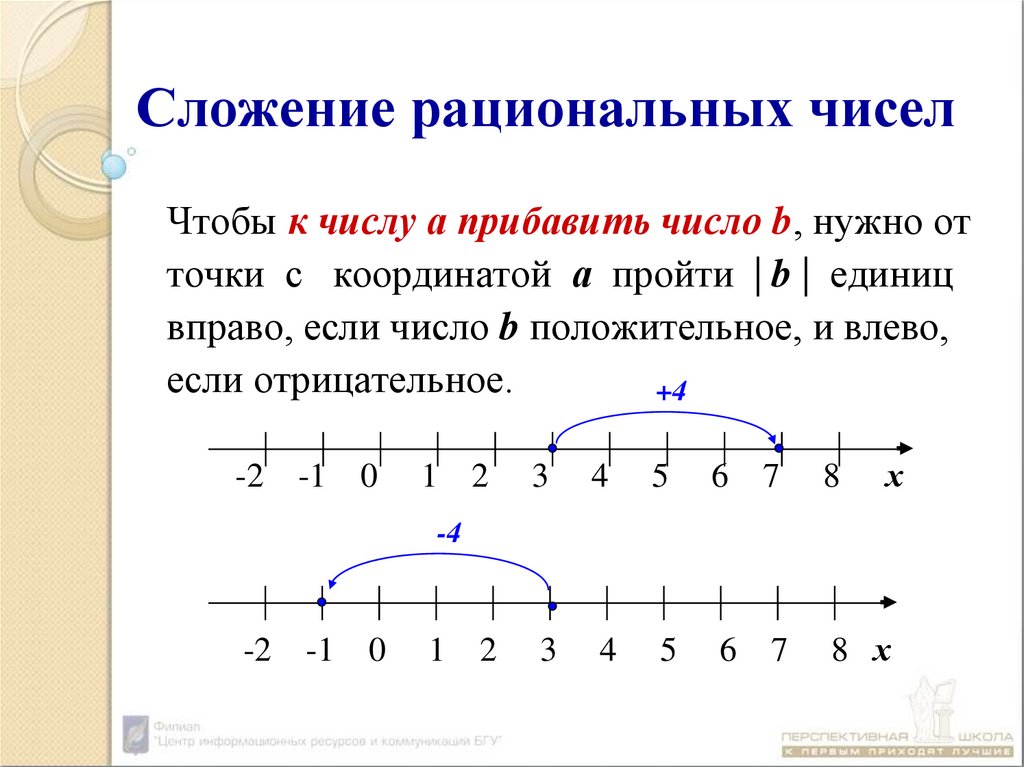
3. Сложение рациональных чисел
Чтобы к числу а прибавить число b, нужно отточки с координатой а пройти | b | единиц
вправо, если число b положительное, и влево,
если отрицательное.
+4
-2
-1 0
1
х
2
3
4
5
6
7
8
2
3
4
5
6
7
8 х
-4
-2
-1 0
1
4. Сложение рациональных чисел
Чтобы сложить два отрицательных числа,нужно сложить их модули и результат
записать со знаком «минус».
+(-5)
-9 -8 -7 -6 -5 -4 -3 -2 -1 0
5 единиц
3 единицы
(5 + 3) единиц
-3 + (-5) = - (|-3| + |-5|) = - (3 + 5) = -8
1
5. Сложение рациональных чисел
Чтобы сложить два числа с разнымизнаками, нужно из большего модуля вычесть
меньший и результат записать со знаками того
числа, модуль которого больше.
+(- 6)
-2
-1 0
+2
1
2
3
4 5 6 7
+8 + (-6) = +2
-9 -8 -7 -6 -5 -4 -3 -2 -1
0
-8 + (+2) = -6
8
1
6. Свойства сложения рациональных чисел
Сложение рациональных чисел имеетпереместительное
и
сочетательное
свойства.
a+b=b+a
a + (b + c) = (a + b) + c
7. Свойства сложения рациональных чисел
• Свойство нуля:а + 0 = а, 0 + а = а
• Сумма противоположных чисел равна
нулю:
а + (-а) = 0
8. Вычитание рациональных чисел
Чтобы вычесть число, можно куменьшаемому
прибавить
число,
противоположное вычитаемому:
а - b = a + (-b) ,
а – (-b) = a + b .
9. Алгебраическая сумма
Любоевыражение,
содержащее
действия вычитания и сложения, можно
рассматривать как сумму.
17 – 4 – (-3) = 17 + (-4) + 3;
(-21) + 7 – m = (-21) + 7 + (– m).
Такие
выражения
называются
алгебраическими суммами.
10. Вычитание рациональных чисел
• Для любых двух рациональных чиселможно найти разность.
• Разность
положительна,
если
уменьшаемое больше вычитаемого, и
отрицательна,
если
уменьшаемое
меньше вычитаемого.
18 – (-6) = 24
3 - 17 = -14
(18 > -6);
(3 < 17).
11. Свойство нуля при вычитании
• Разность равных чисел равна нулю:а–а=0 .
• Вычитание нуля не изменяет числа:
а–0=а .
• Если уменьшаемое равно нулю, то
разность есть число, противоположное
вычитаемому:
0 – а = -а .
12. Нахождение длины отрезка
Чтобы найти длину отрезка по известнымкоординатам его конца, нужно из большей
координаты вычесть меньшую.
l
М
-10 -8 -6
N
-4 -2 0
2
4
l = 8 – (-6) = 14.
Значит, MN = 14.
6
8
10
13. Умножение рациональных чисел
Правило умножения рациональныхчисел с одинаковыми знаками:
чтобы
умножить
два
числа
с
одинаковыми
знаками,
нужно
перемножить их модули и результат
записать со знаком «+».
(+5) ∙ (+8) = +(5 ∙8) = +40 = 40;
(-6) ∙ (-9) = +(6 ∙ 9) = +54 = 54.
14. Умножение рациональных чисел
Правило умножения рациональныхчисел с разными знаками:
чтобы умножить два числа с разными
знаками, нужно перемножить их модули
и результат записать со знаком «-».
(-7) ∙ (+6) = -(7 ∙ 6) = -42;
(+9) ∙ (-4) = -(9 ∙ 4) = -36.
15. Свойства умножения рациональных чисел
• Переместительноеа ∙ b = b ∙ a.
• Cочетательное
а ∙ (b ∙ c) = (а ∙ b) ∙ c.
• Распределительное
а ∙ (b + c) = а ∙ b + a ∙ c;
а ∙ (b - c) = а ∙ b - a ∙ c.
• Свойство нуля
а ∙ 0 = 0, 0 ∙ a = 0.
16. Свойства умножения рациональных чисел
• Если произведение равно нулю, то хотя бы одиниз множителей равен нулю:
если аb = 0, то а = 0 или b = 0.
• Если один из множителей равен 1, то
произведение равно другому множителю.
а ∙ 1 = а, 1 ∙ a = а.
• Если один из множителей равен -1, то
произведение
является
числом,
противоположным другому множителю.
а ∙ (-1) = -а, -1 ∙ a = -а.
17. Деление рациональных чисел
Число, обратноеотрицательное.
отрицательному
числу,
также
Правило деления рациональных чисел с
одинаковыми знаками:
чтобы разделить два числа с одинаковыми
знаками, нужно модуль делимого разделить на
модуль делителя и результат записать со
знаком «+».
(-9) : (-3) = 3;
153 : 9 = 17.
18. Деление рациональных чисел
Правило деления рациональных чисел сразными знаками:
чтобы разделить два числа с разными знаками,
нужно модуль делимого разделить на модуль
делителя и результат записать со знаком «-».
5 : 2 5 3 15 1 1 .
14
14
7 3
7 2
19. Свойства деления рациональных чисел
• Если делимое равно 0, а делитель не равен 0,то частное равно 0:
0:а=0
• На нуль делить нельзя!
• Деление на единицу не изменяет числа:
а:1=а
• При делении на -1 получается число,
противоположное делимому:
а : (-1) = -а
20. Основное свойство частного
Частное не изменится, если делимое иделитель одновременно умножить или
разделить на одно и то же не равное
нулю число:
(а ∙ k) : (b ∙ k) = a : b,
(а : k) : (b : k) = a : b.
21. Свойства деления рациональных чисел
Деление рациональных чисел имеетраспределительные свойства
относительно
сложения
(а + b) : c = a : c + b : c
относительно
вычитания
(а - b) : c = a : c - b : c




















 mathematics
mathematics








