Similar presentations:
Числа. Натуральные числа. Действия над натуральными числами
1. Числа
Первое чудо,которое
подарила нам
математика,
это числа.
2. Натуральные числа
1 211
21
29
3 4
12 13
5
14
22 23 24
30
31
6
7
15
8
32
33
10
17
16
25
9
26 27
34 35
19
18
20
28
36
37
3. Натуральные числа
12
3
4
5
9
11
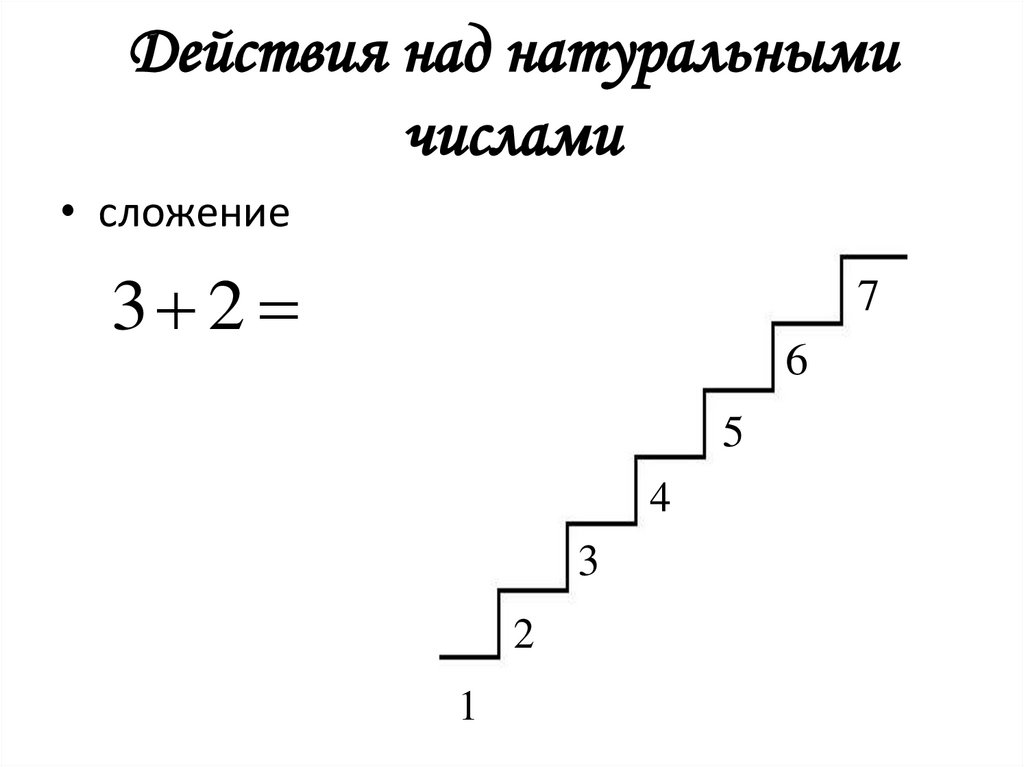
4. Действия над натуральными числами
• сложение3 2
7
6
5
4
3
2
1
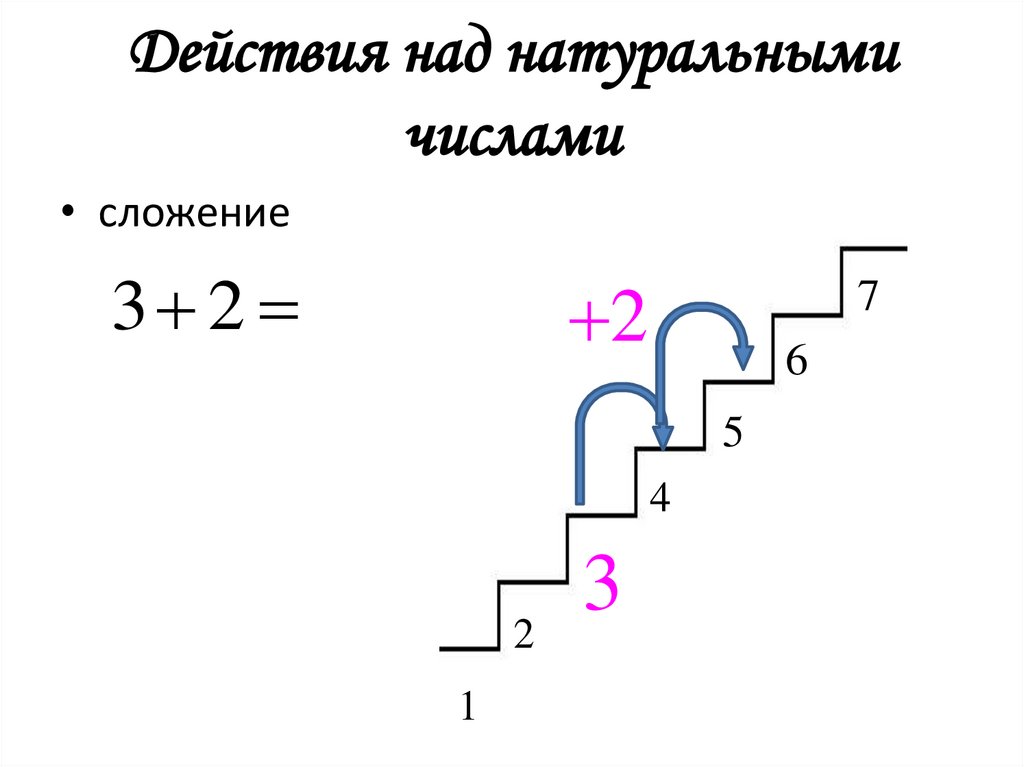
5. Действия над натуральными числами
• сложение3 2
2
7
6
5
4
2
1
3
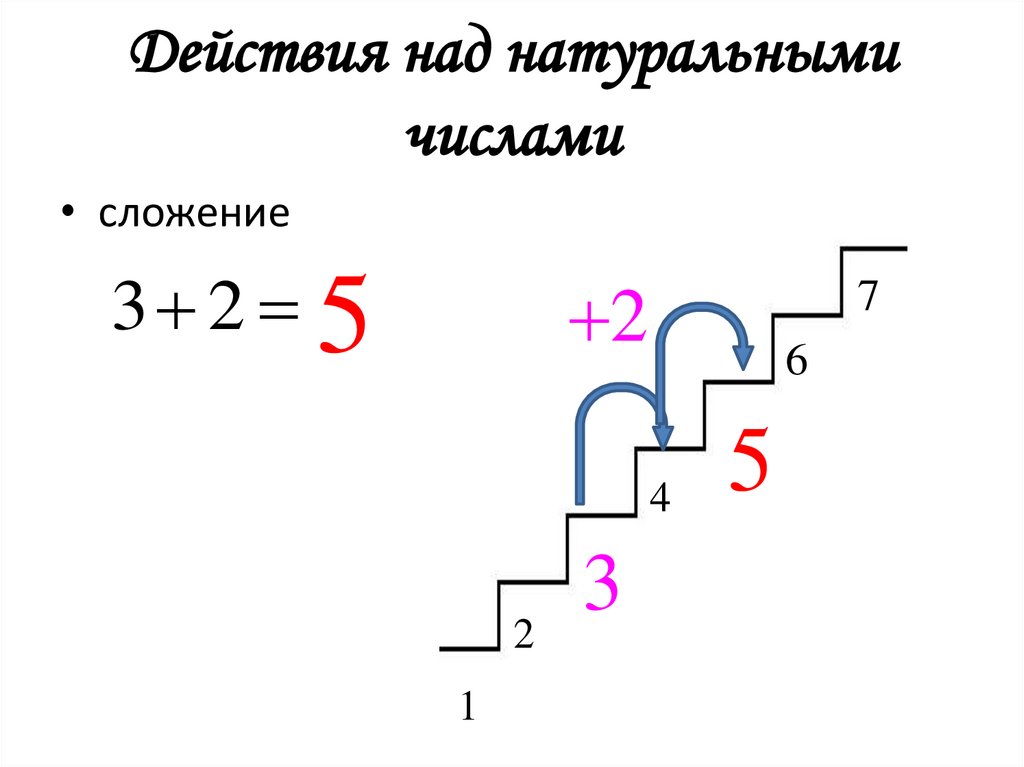
6. Действия над натуральными числами
• сложение3 2 5
2
7
6
4
2
1
3
5
7. Сложение на множестве натуральных чисел
a N;b Na b c
c N
• сложение всегда выполнимо на
множестве натуральных чисел
• множество натуральных чисел
замкнуто относительно сложения
8. Сложение
Складывать можно:• На пальцах
• В уме
• На калькуляторе
9. Свойства сложения
• коммутативностьa b b a
• ассоциативность
a b c a b c
10. Действия над натуральными числами
• вычитаниеa b x
такое что
x b a
Вычесть из числа а число б, значит
найти такое число х,
которое при сложении с б даст а
11. Действия над натуральными числами
• вычитание7 3
7
6
5
4
3
2
1
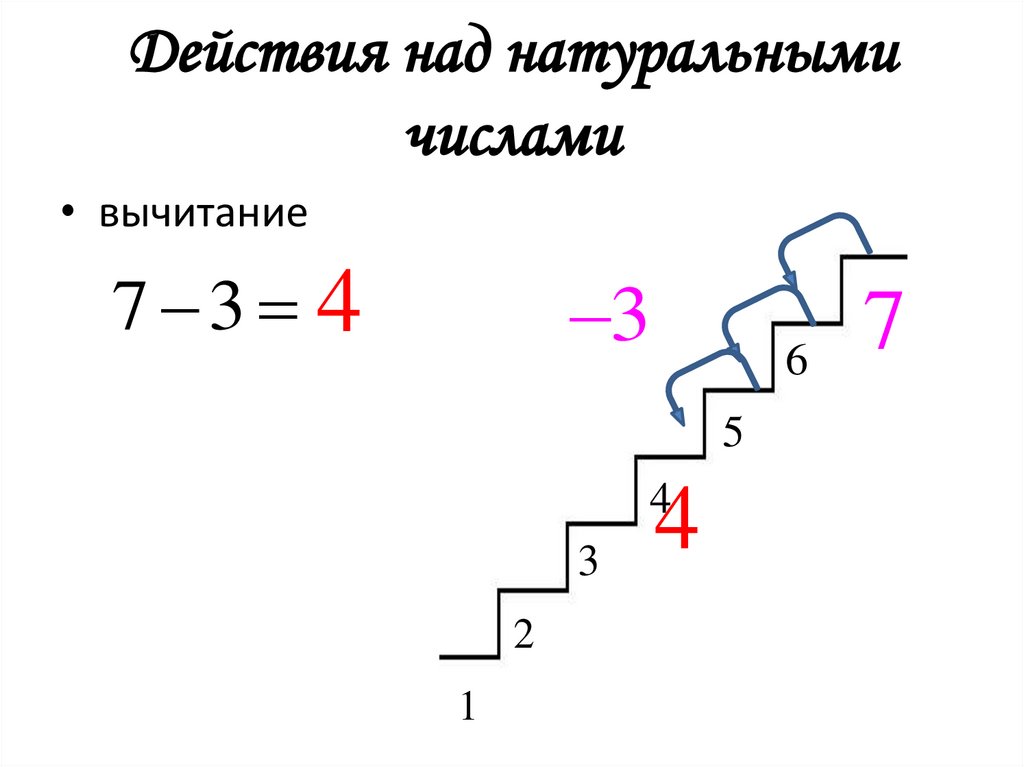
12. Действия над натуральными числами
• вычитание7 3 4
3
6
5
4
3
2
1
4
7
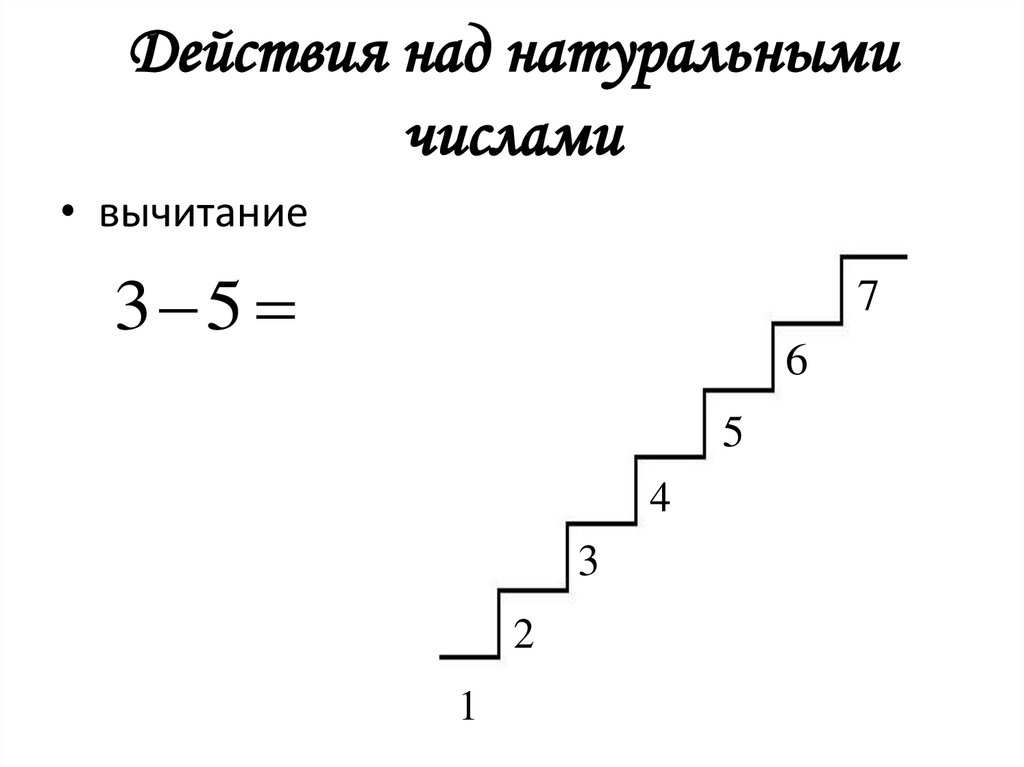
13. Действия над натуральными числами
• вычитание3 5
7
6
5
4
3
2
1
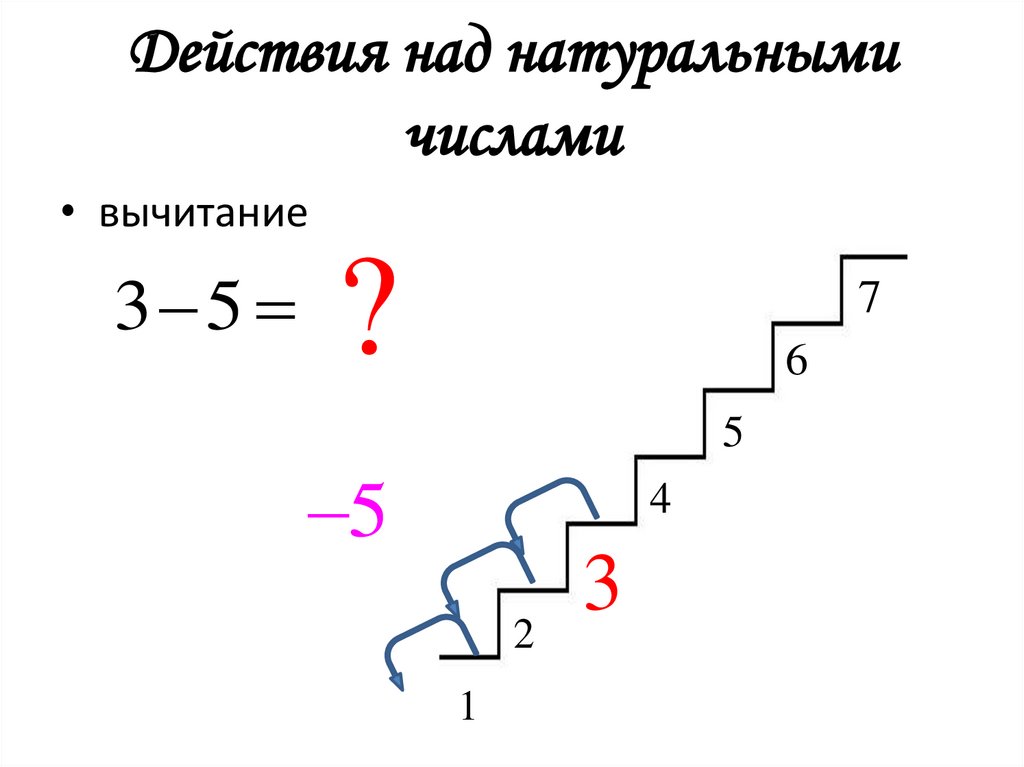
14. Действия над натуральными числами
• вычитание3 5
?
7
6
5
5
4
2
1
3
15. Вычитание на множестве натуральных чисел
a N;b Na b c
c N
c N
• вычитание не всегда выполнимо на
множестве натуральных чисел
множество натуральных чисел не
замкнуто относительно вычитания
16.
Действия над натуральнымичислами
умножение
a b a a a ... a
b раз
Умножить число а на число б, это значит
найти сумму б слагаемых, каждое из
которых равно а
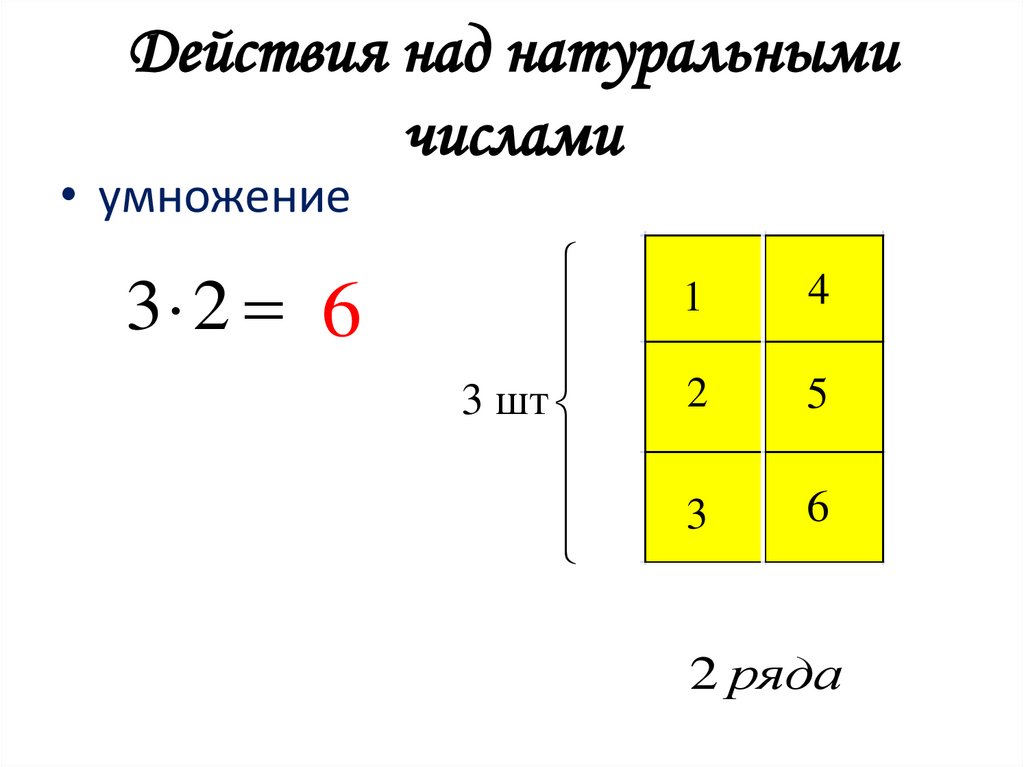
17. Действия над натуральными числами
• умножение3 2 6
3 шт
1
4
2
5
3
6
..........
2 ряда
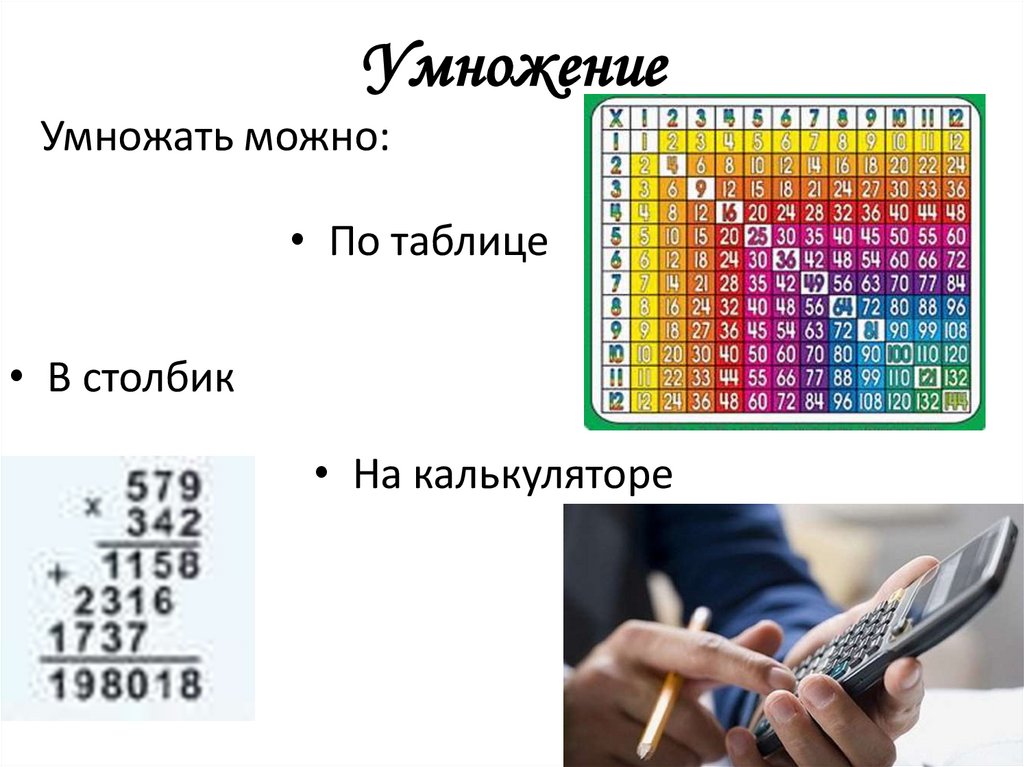
18. Умножение
Умножать можно:• По таблице
• В столбик
• На калькуляторе
19. Свойства умножения
• коммутативность• ассоциативность
a b b a
a b c a b c
• дистрибутивность относительно сложения
a b c aс bc
20.
2 10 35 12 35a b c aс bc
2 10 35 2 35
10 35
70 350 420
21. Действия над натуральными числами
• делениеa:b x
такое что
x b a
Разделить число а на число б, значит
найти такое число х,
которое при при умножении на б даст а
22. Действия над натуральными числами
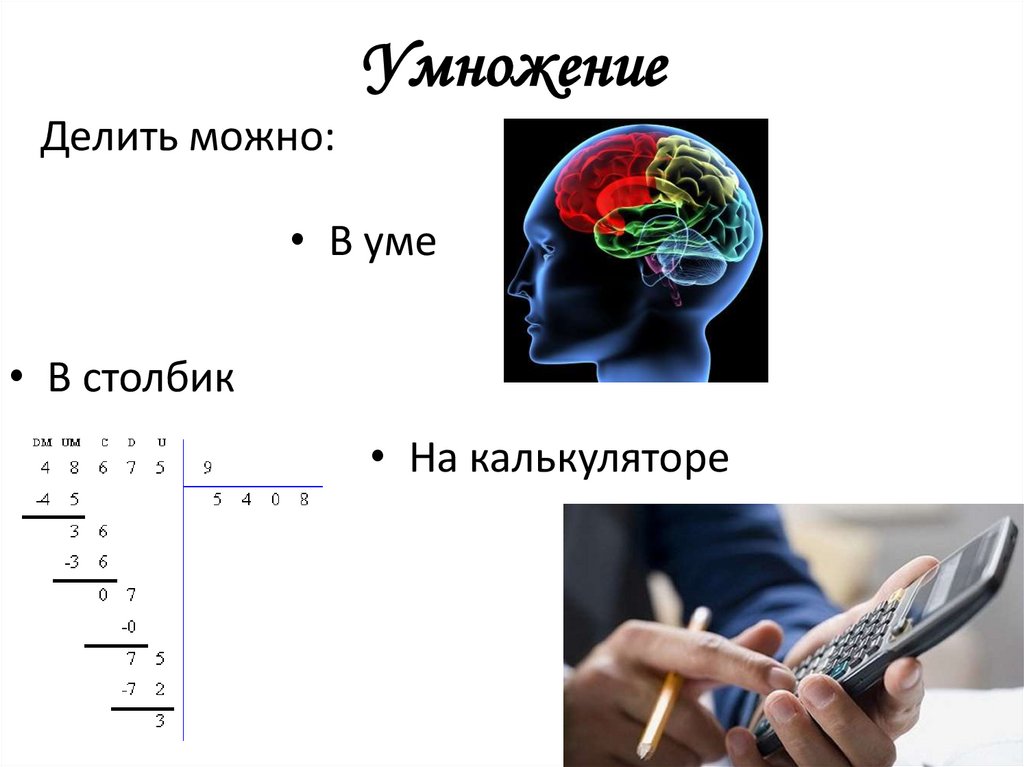
• Деление23. Умножение
Делить можно:• В уме
• В столбик
• На калькуляторе
24. На множестве натуральных чисел деление выполнимо не всегда
17 : 3 ?25.
На ноль делить нельзя!!Разделить число а на число б, значит
найти такое число х,
которое при при умножении на б даст а
a:b x
5: 0 x
такое что
x b a
x 0 5
26.
На ноль делить нельзя!!Разделить число а на число б, значит
найти такое число х,
которое при при умножении на б даст а
a:b x
5: 0 x
такое что
x b a
x 0 5
27.
На ноль делить нельзя!!Разделить число а на число б, значит
найти такое число х,
которое при при умножении на б даст а
a:b x
5:0 x
такое что
x b a
x 0 5
28. Признаки делимости чисел
• На 2• делятся числа, заканчивающиеся
нулем или четным числом
14582698
2
29. Признаки делимости чисел
• На 2делятся числа, заканчивающиеся нулем
или четным числом
14582698
3652987
2
Т.к.
Не делится на 2
8 2
30. Признаки делимости чисел
• На 2делятся числа, заканчивающиеся нулем
или четным числом
14582698
3652987
2
Т.к.
8 2
Не делится на 2
Т.к. 7 - нечетное
31. Признаки делимости чисел
• На 5• делятся числа, заканчивающиеся
нулем или цифрой 5
14582690
5
32. Признаки делимости чисел
• На 5• делятся числа, заканчивающиеся
нулем или цифрой 5
14582690
3652985
5
33. Признаки делимости чисел
• На 5• делятся числа, заканчивающиеся
нулем или цифрой 5
14582690
3652985
75312696
5
34. Признаки делимости чисел
• На 5• делятся числа, заканчивающиеся
нулем или цифрой 5
14582690
3652985
75312696
5
35. Признаки делимости чисел
• На 10• делятся числа, заканчивающиеся
нулем
14582690
3652985
75312696
10
36. Признаки делимости чисел
• На 4делятся числа,
заканчивающиеся на два нуля
если две последние цифры
выражают число, делящееся на 4
14582600
36582608
45687616
14582645
4
14582663
37. Признаки делимости чисел
• На 25делятся числа,
заканчивающиеся на два нуля
если две последние цифры
выражают число, делящееся на 25
14582600
36582650
45687625
14582645
25
14582663
38. Признаки делимости чисел
• На 3делятся числа, сумма цифр которых
делится на 3
1458369
3
1 4 5 8 3 6 9 36
3 6 9
93
39. Признаки делимости чисел
• На 3делятся числа, сумма цифр которых
делится на 3
653127
3
6 5 3 1 2 7 24
2 4 6
63
40. Признаки делимости чисел
• На 3делятся числа, сумма цифр которых
делится на 3
69124379
6 9 1 2 4 3 7 9 41
4 1 5
5 не делится на 3
41. Признаки делимости чисел
• На 9делятся числа, сумма цифр которых
делится на 9
2458368
9
2 4 5 8 3 6 8 36
3 6 9
99
42. Признаки делимости чисел
• На 9делятся числа, сумма цифр которых
делится на 9
69124379
6 9 1 2 4 3 7 9 41
41 не делится на 9
43. Простые и составные числа
• Число называется простым, если делитсятолько на ноль и себя
2 3 5
11
13
123
• Если число имеет больше двух натуральных
делителей, оно называется составным
4
1 2 4
6
12 3 6
?
46
141
87
44. N+0
01
2
3
множество
неотрицательных целых чисел
45. Целые числа
12
3
1
2
3
7
6
6
4
5
4
5
8
7
9
8
9
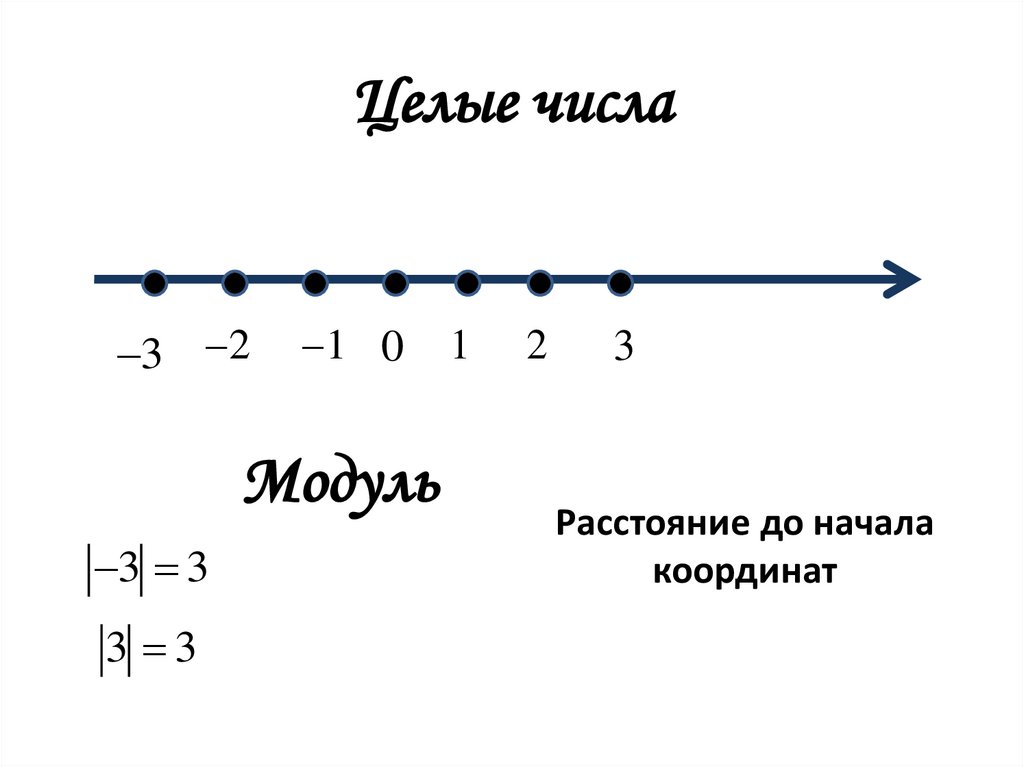
46. Целые числа
3 21 0
Модуль
3 3
3 3
1
2
3
Расстояние до начала
координат
47. Целые числа
СложениеСложение чисел с одинаковыми знаками
3 5 8
3 5 3 5 3 5 8
Сложение чисел с разными знаками
3 5 3 5 5 3 2
3 5 5 3 2
Вычитание
3 5 3 5 8
3 5 3 5 2
48. Целые числа
Умножение и делениеплюс на плюс
и
минус на минус
дают
плюс
3 5 15
3 5 15
3 5 15
3 5 15
15
5
3
15
5
3
15
5
3
плюс на минус
минус на плюс
дают
минус
49. Возведение в степень
an
а – основание степени
n – показатель степени
a a a a ... a a
n
n раз
50.
2 2 2 2 83
3 разa
3 3 3 9
2
5
2
2 разa
3
4
5 5 5 125
3 разa
2 2 2 2 16
4 разa
51. Свойства степени
a a an
m
n
a
n m
a
m
a
1
m
a
m
a
n m
2 2 23 5 28
3
5
5
2
5 3
2
2 2 4
3
2
1
3
2
3
2
52. Свойства степени
an m
n
a
a a
m
a a
n m
m
n
1
2
2
3 4
5
23 4 212
2 2
3
a 1
3
5
0
1 1
n
a a
1
53. Свойства степени
a a an
m
a
m
n
n m
a
n m
n
a
n m
a
m
a
1
m
a
m
a
1 1
n
n
a a
m
m
n
a a
a 1
0
a a
1
1
2
54. Z - множество целых чисел
Множество целых чисел замкнутоотносительно:
• Сложения
a, b Z ; a b Z
• Вычитания
a, b Z ; a b c; c Z
a, b Z ; a b c;
• Умножения
Но
Незамкнуто относительно деления
c Z
2 2
2,3 Z ; 2 : 3 ; Z
3 3
55. Дробные числа
Обыкновенные дробиa
b
а –сколько таких частей взяли
b- на сколько частей разделили
56. Дробные числа
Обыкновенные дробиa
b
а –числитель
b- знаменатель
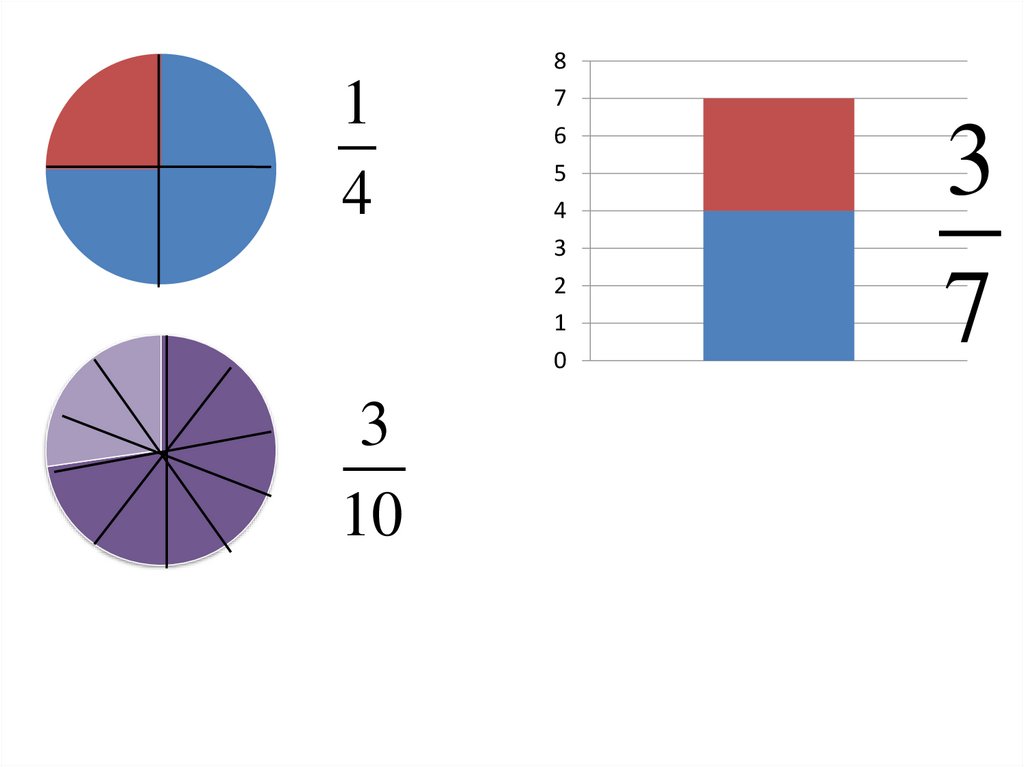
57.
14
3
10
8
7
6
5
4
3
2
1
0
3
7
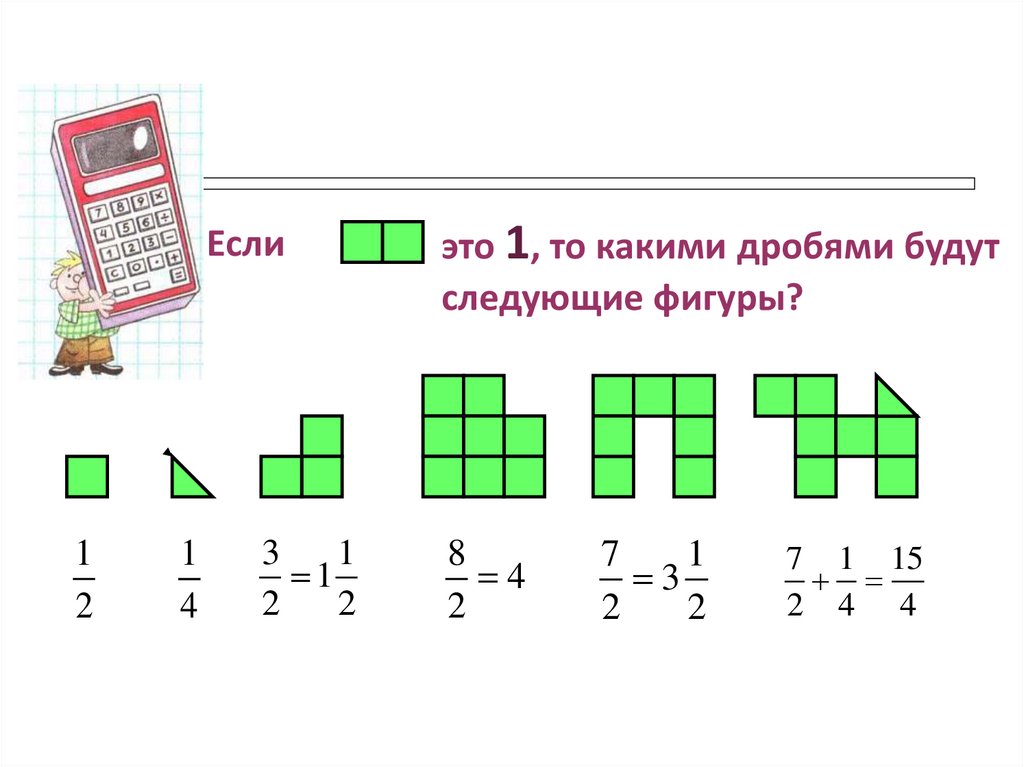
58.
Если1
2
1
4
3
1
1
2
2
это 1, то какими дробями будут
следующие фигуры?
8
4
2
7
1
3
2
2
7 1 15
2 4 4
59. Дробные числа
смешанные дроби1
3
2
3
16
8
Превратить смешанную дробь в неправильную
1 3 2 1
3
2
2
3 5 7 3 38
5
7
7
7
60. Дробные числа
Сложение и вычитаниедробей с одинаковым знаменателем
a c a c
b b
b
3 1 3 1 4
5 5
5
5
5 2 5 2 3
7 7
7
7
61. Дробные числа
Сложение и вычитаниедробей с разным знаменателем
сначала подвести под общий знаменатель
a c ad cb
b d
bd
5 2 5 3 2 7 15 14 1
7 3
7 3
21
21
62. Дробные числа
Сложение и вычитаниедробей с разным знаменателем
сначала подвести под общий знаменатель
a c an cm
b d
k
k - общий знаменатель – число, которое
делится на b и d
63. Дробные числа
Сложение и вычитаниедробей с разным знаменателем
сначала подвести под общий знаменатель
a
k :b n
b
c an cm
d
k
k - общий знаменатель – число, которое
делится на b и d
64. Дробные числа
Сложение и вычитаниедробей с разным знаменателем
сначала подвести под общий знаменатель
a
k :b n
b
c an cm
d
k
k - общий знаменатель – число, которое
делится на b и d
65. Дробные числа
Сложение и вычитаниедробей с разным знаменателем
сначала подвести под общий знаменатель
n
k :d m
a
c
b
d
an cm
k
k - общий знаменатель – число, которое
делится на b и d
66. Дробные числа
Сложение и вычитаниедробей с разным знаменателем
сначала подвести под общий знаменатель
n
k :d m
a
c
b
d
an cm
k
k - общий знаменатель – число, которое
делится на b и d
67. Дробные числа
Сложение и вычитаниедробей с разным знаменателем
сначала подвести под общий знаменатель
a
k :b n
b
c
k :d m
d
an cm
k
k - общий знаменатель – число, которое
делится на b и d
5 1 5 3 1 2
6 9
18
68. Дробные числа
Сложение и вычитаниедробей с разным знаменателем
сначала подвести под общий знаменатель
a
k :b n
b
c
k :d m
d
an cm
k
k - общий знаменатель – число, которое
делится на b и d
3
2
5
1
5 3 1 2
6
9
18
69. Дробные числа
Сложение и вычитаниедробей с разным знаменателем
сначала подвести под общий знаменатель
a
k :b n
b
c
k :d m
d
an cm
k
k - общий знаменатель – число, которое
делится на b и d
3
2
15 2 13
5
1
5 3 1 2
18
18
6
9
18
70.
ak :b n
b
c
k :d m
d
an cm
k
4 8
4 3 8 1
5 15
15
15 5
15 15
71.
ak :b n
b
c
k :d m
d
an cm
k
4 8
4 3 8 1
5 15
15
15 : 5 3
15 :15 1
72.
ak :b n
b
3
1
c
k :d m
d
an cm
k
4
8
4 3 8 1
15
5 15
15 : 5 3
15 :15 1
73.
ak :b n
b
3
1
c
k :d m
d
an cm
k
4
8
4 3 8 1 12 8 20 4 1 1
15 3
3
15
15
5 15
15 : 5 3
15 :15 1
74. Дробные числа
Сокращение дробейЧислитель и знаменатель дроби можно
разделить на одно и то же число
15
20
75. Дробные числа
Сокращение дробейЧислитель и знаменатель дроби можно
разделить на одно и то же число
15
20
\3
\4
7
21
3
4
15 15 : 5 3
20 20 : 5 4
7
7:7
21 21: 7
76. Дробные числа
Сокращение дробейЧислитель и знаменатель дроби можно
разделить на одно и то же число
15
\3
20
7
\4
3
4
15 15 : 5 3
20 20 : 5 4
\1
1
\3
3
21
7
7:7
21 21: 7
77. Дробные числа
Сокращение дробейЧислитель и знаменатель дроби можно
разделить на одно и то же число
6 10
25 9
78. Дробные числа
Сокращение дробейЧислитель и знаменатель дроби можно
разделить на одно и то же число
6 10
25 9
79. Дробные числа
Сокращение дробейЧислитель и знаменатель дроби можно
разделить на одно и то же число
\2
6 10
25 9
\3
80. Дробные числа
Сокращение дробейЧислитель и знаменатель дроби можно
разделить на одно и то же число
\2
6 10
\2
\5
\3
25 9
2
2
4
5 3 15
81. Дробные числа
Сокращение дробейсокращать нельзя,
если есть сложение или вычитание
10 3
15
82. Дробные числа
Сокращение дробейсокращать нельзя,
если есть сложение или вычитание
\2
10 3
15
\3
1
15
НО
10 3 7
15
15
83. Дробные числа
Сокращение дробейсокращать нельзя,
если есть сложение или вычитание
\2
10 3
15
\3
1
15
НО
10 3 7
15
15
84. Дробные числа
Умножениеa c a c
b d b d
85. Дробные числа
Умножениеa c a c
b d b d
86. Дробные числа
Умножениеa c a c
b d b d
3 2 3 2 6
7 5 7 5 35
Деление
a c a d a d
:
b d b c b c
87. Дробные числа
Умножениеa c a c
b d b d
3 2 3 2 6
7 5 7 5 35
Деление
a c a d
:
b d b c
3 2 3 5 15
:
7 5 7 2 14
88. Дробные числа
Десятичные дробидроби со знаменателем
0.1
0.03
0.125984
10
n
15.0849
Преобразование обыкновенной дроби в
десятичную
1
1: 2 0.5
2
2
2: 25 0.08
25
89.
Преобразование обыкновенной дроби вдесятичную
1
Бесконечные
0.33333333...
3
десятичные
5
0.555555...
периодические
9
7
дроби
0.63636363...
11
2
0.285714285714285714...
7
90.
Преобразование обыкновенной дроби вдесятичную
1
Бесконечные
0.33333333...
3
десятичные
5
0.555555...
периодические
9
7
дроби
0.63636363...
11
2
0.285714285714285714...
7
91.
Преобразование обыкновенной дроби вдесятичную
1
Бесконечные
0.333... 0.(3)
3
десятичные
5
0.555... 0.(5)
периодические
9
7
0.6363... 0.(63) дроби
11
2
0.285714285714... 0. 285714
7
92. Дробные числа
Преобразование десятичной дроби вобыкновенную
\1
25
25
1
0.25
\4
100
4
100
\2
4
4
2
0.4
\5
10 10
5
0.458496
93. Дробные числа
Преобразование десятичной дроби вобыкновенную
25
25 : 25 1
0.25
100 100 : 25 4
4 4:2 2
0.4
10 10 : 2 5
458496 :16
1791
458496
0.458496
1 000000 1000000 :16 62500
6 знаков
6 нулей
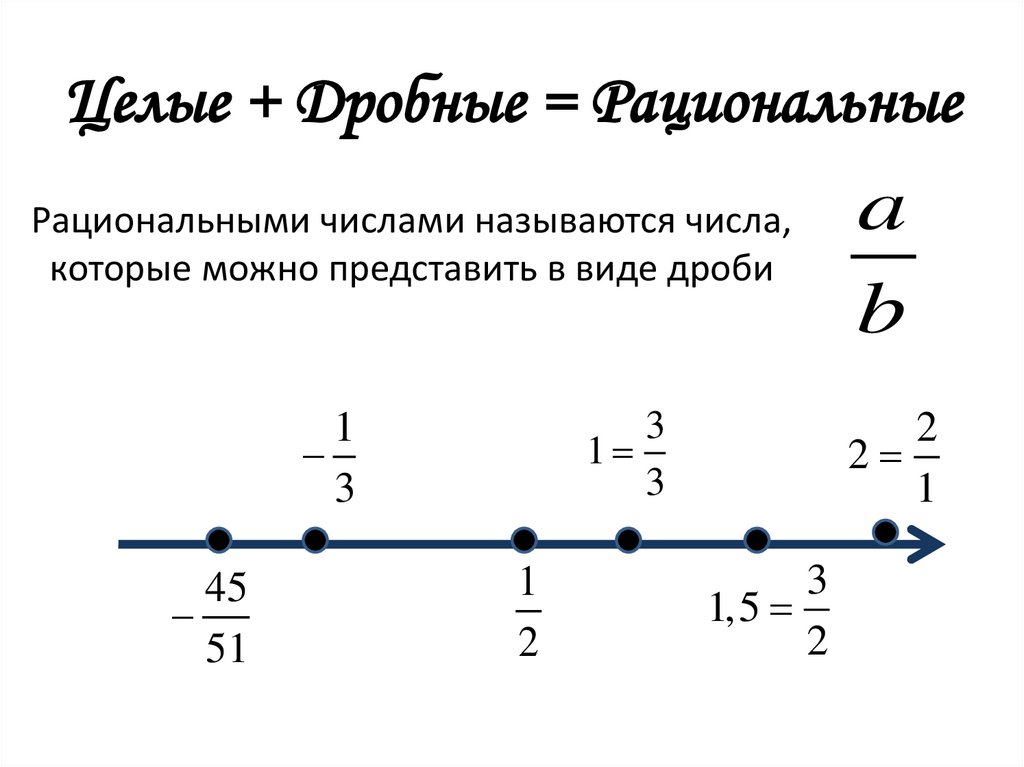
94. Целые + Дробные = Рациональные
Рациональными числами называются числа,которые можно представить в виде дроби
3
1
3
1
3
45
51
1
2
a
b
2
2
1
3
1,5
2
95. Одно и то же рациональное число может быть записано разными способами:
1 2 25Но среди всех
0.5
...
2 4 50
записей одна
и только одна
1 2 3
0. 3 ...
несократимая
3 6 9
обыкновенная
1 13 26
2.1 6 2
... дробь
12
6 6
96. Одно и то же рациональное число может быть записано разными способами:
1 2 25Но среди всех
0.5
...
2 4 50
записей одна
и только одна
1 2 3
0. 3 ...
несократимая
3 6 9
обыкновенная
1 13 26
2.1 6 2
... дробь
12
6 6
97. Рациональные
Любоерациональное число
можно представить
в виде
несократимой
обыкновенной дроби
a
b
98. Домашнее задание
55
1
10 230.04 46.75
13 2
27
6
4
0.01
2
2
3
3
2
3
2
4
1
0 1
5
6
1
2 10 1
Проверочная работа























































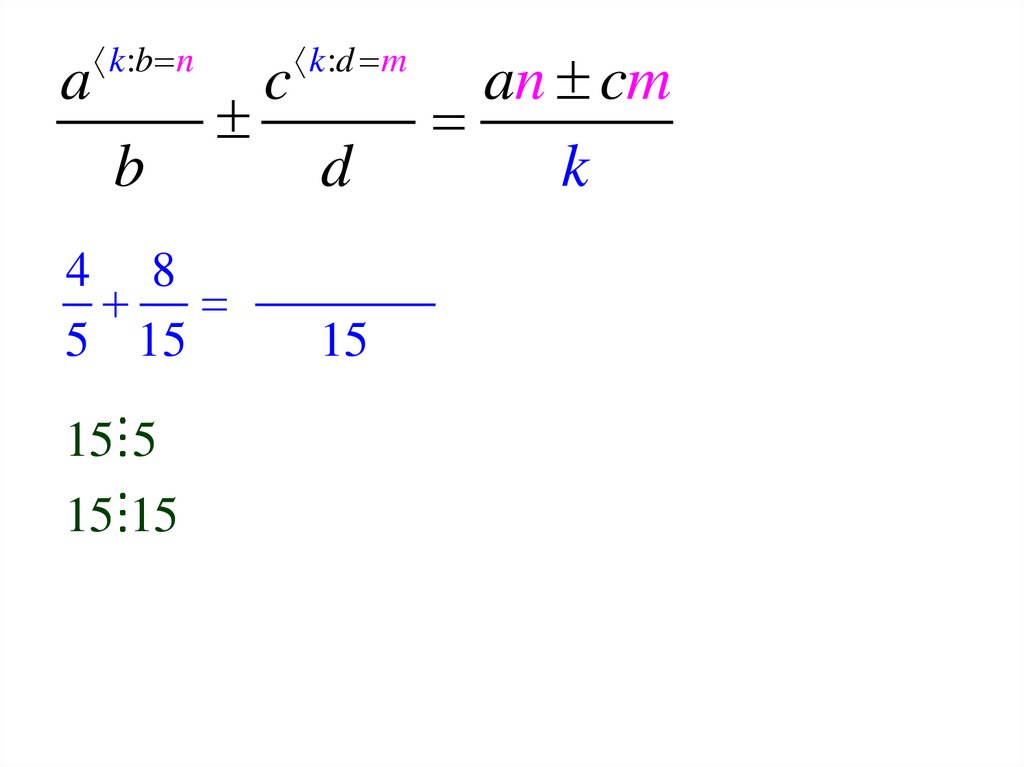
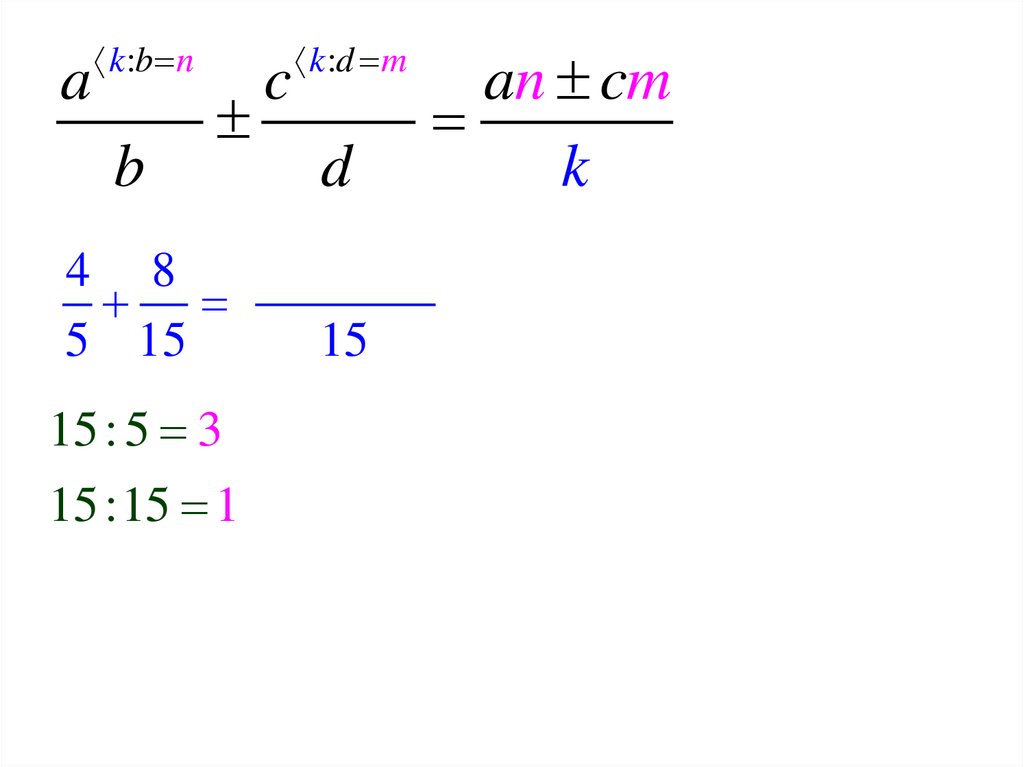
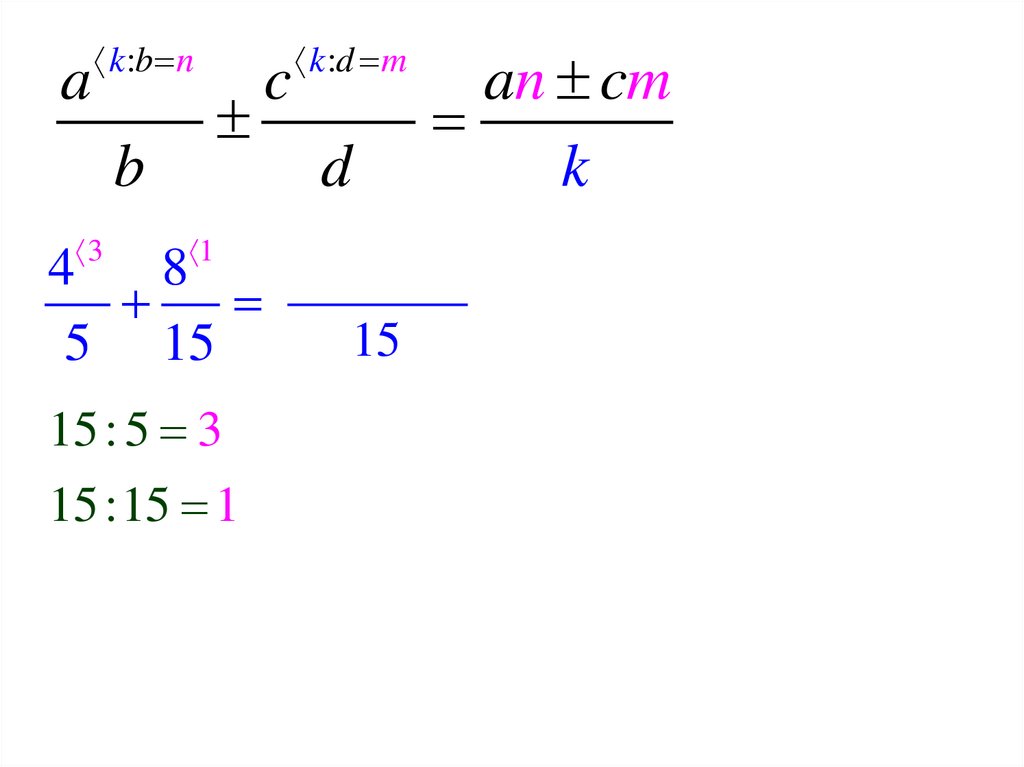
























 mathematics
mathematics