1.27M

Category: $mathematics$ mathematics

Геометрия. Повторение

1. Модуль «Геометрия»

Урок 1_Повторение

2. Вспомним:

1)Площадь прямоугольного треугольника с катетами a, b
2)Площадь треугольника, если известен угол между сторонами
3)Площадь круга
4)Площадь трапеции
5)Площадь параллелограмма, если известна высота
6)Площадь параллелограмма, если известен угол между смежными
сторонами
7)Длина окружности
8)Средняя линия треугольника
9)Средняя линия трапеции
10)Теорема Пифагора
11)Теорема косинусов
12)Теорема синусов
13)Длина дуги окружности

3.

Определите верность утверждения:
1.Если угол равен 56⁰, то вертикальный с ним угол равен
124⁰.
2. Если два угла треугольника равны 65⁰ и 70⁰, то третий
угол равен 45⁰.
3.Диагонали равнобедренной трапеции равны.
4. Площадь треугольника равна половине произведения
его смежных сторон на синус угла между ними.

4.

5. Через любые три различные точки плоскости можно
провести единственную прямую.
6. Отношение сходственных сторон двух подобных
треугольников равно коэффициенту подобия
7. Катет прямоугольного треугольника больше
гипотенузы.
8.Если угол равен 25⁰, то смежный с ним угол равен 145⁰

5.

9. В остроугольном треугольнике два прямых угла.
10. Два треугольника подобны, если два угла одного
треугольника соответственно равны двум углам другого
треугольника.
11. Средняя линия треугольника равна двум основаниям.
12. Диагонали параллелограмма точкой пересечения
делятся пополам
13. Вписанный угол, опирающийся на диаметр – прямой.

6.

На клетчатой бумаге изображен угол.
Найдите его синус.
В
ВС 3 0,6
Sin A =
АВ 5
3
С
А
АВ АС ВС 4 3 16 9 25 5
2
2
2
2
Ответ: 0,6

7.

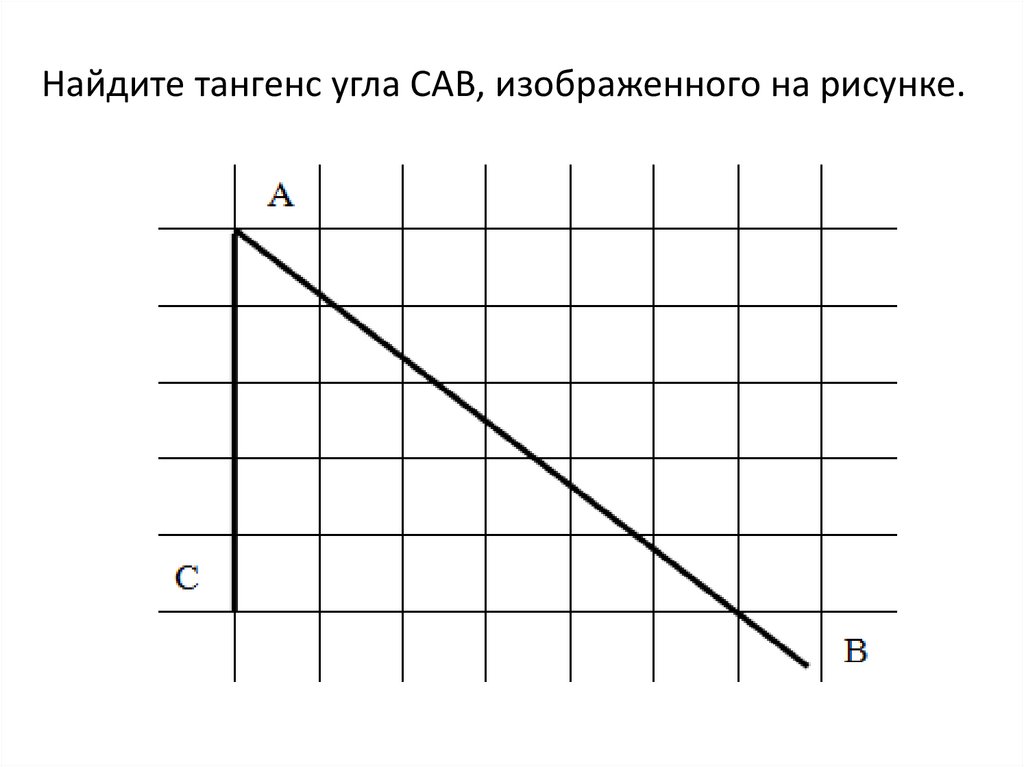
Найдите тангенс угла САВ, изображенного на рисунке.

8. Вспомним:

sin
tg
cos
Формулы приведения
sin (1800 - ) = sin
cos (1800 - ) = - cos

9.

На клетчатой бумаге изображен угол.
Найдите его косинус.
- тупой
a
4
cos(1800 - ) = - cos
cos = cos(1800 - ) = - cos
- острый
3
a 4 3 16 9 25 5
2
2
3
cos 0,6
5
cos = - cos = - 0,6
Ответ: -0,6

10.

Самостоятельно
На клетчатой бумаге изображен угол.
Найдите его тангенс.
B
O
A
Ответ: 2

11.

Самостоятельно
На клетчатой бумаге изображен угол.
Найдите его тангенс.
Ответ: -1

12.

Самостоятельно
Найдите синус угла А треугольника АВС,
изображенного на рисунке.
В
А
С
Ответ: 0,8

13.

Самостоятельно
Найдите тангенс угла АОВ,
изображенного на рисунке.
А
О
В
Ответ: 0,5

14. Модуль «ГЕОМЕТРИЯ» №10

В
15
tgA
8
Найти АВ.
15
А
С
ВС
tgA
АC
⇒
ВС 15
АC 8
⇒
AС 8
По теореме Пифагора
2
2
2
2
АВ АC ВС 8 15 17
Ответ: 17.

15.

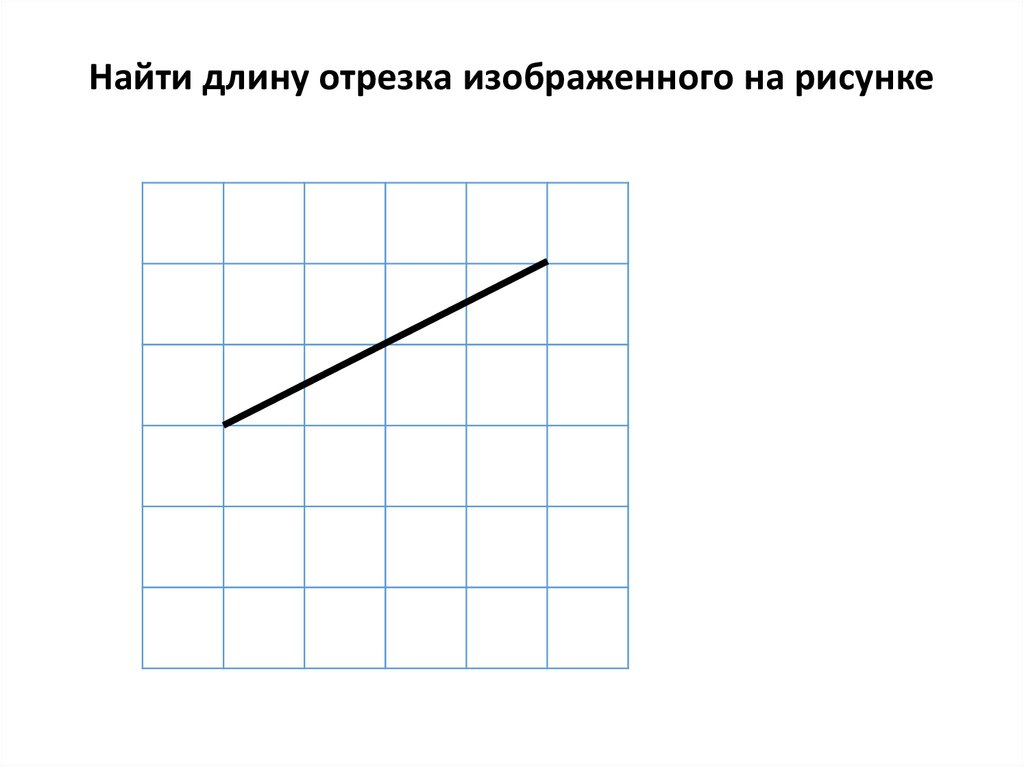
Найти длину отрезка изображенного на рисунке

16.

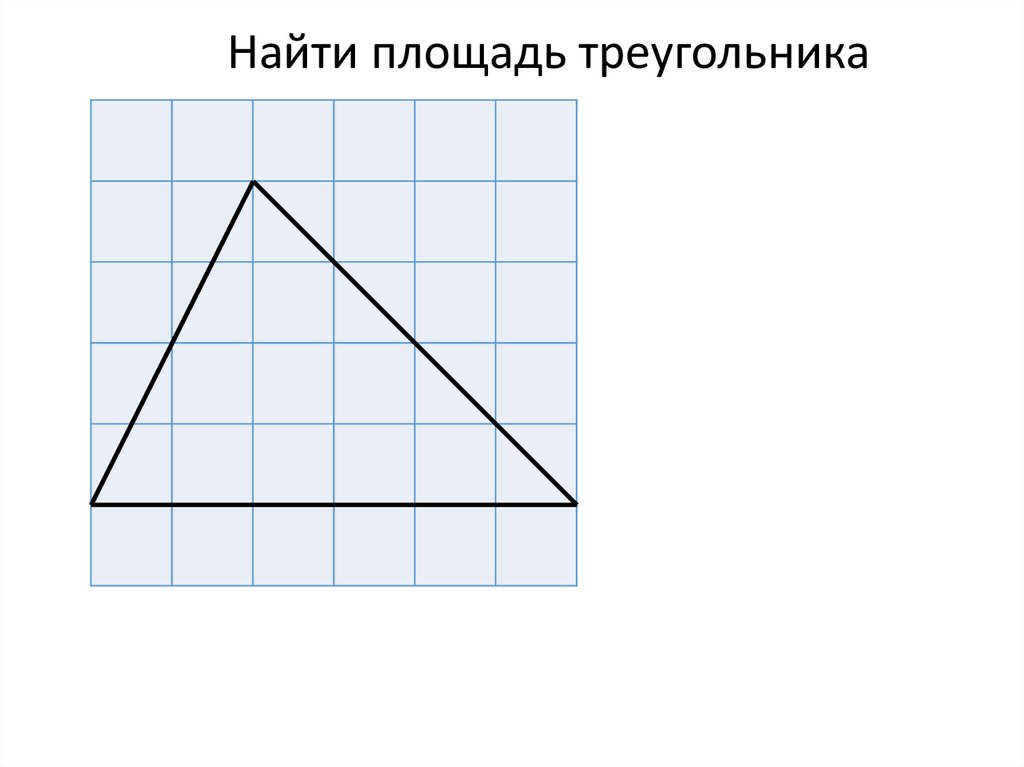
Найти площадь треугольника

17.

Найти площадь трапеции

18.

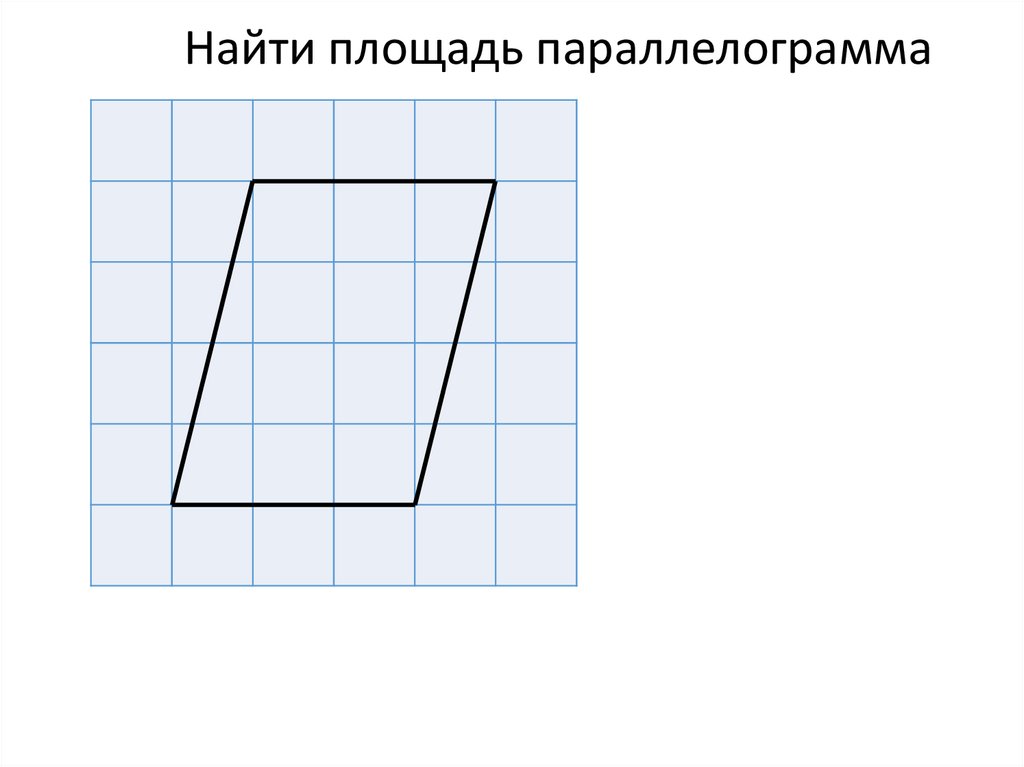
Найти площадь параллелограмма

19.

Найти площадь квадрата

20.

Найти радиус вписанной окружности ромба
.

21. Работа на готовых чертежах

Внешний угол
Угол между двумя секущими
треугольника
равен сумме
двух углов
треугольника,
не смежных с
ним.
(угол110
с вершиной вне окружности)
равен
55 полуразности угловых величин дуг
35
78 : 2 39
окружности, заключенных внутри угла.
90
130 42
х
44
2
30
60
120

22. Модуль «ГЕОМЕТРИЯ» №10

В
1
2
А
3
Е
С Дано: параллелограмм, P=10,
ВЕ – биссектриса, АЕ:ЕD=1:3.
D Найти: AD

23. Модуль «ГЕОМЕТРИЯ» №10

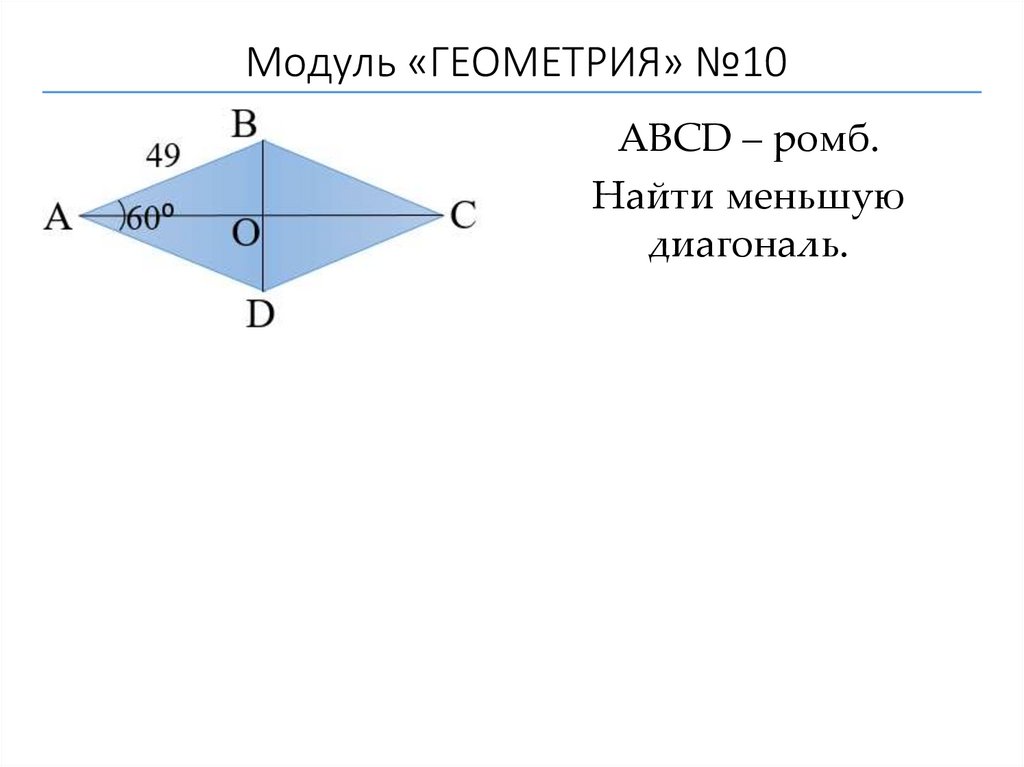
АВСD – ромб.
Найти меньшую
диагональ.

24. Модуль «ГЕОМЕТРИЯ» №10

В
А
r
С
45
D
АВСD – трапеция, P∆ABCD =100.
Найти r.