Similar presentations:
Углы в пространстве. Перпендикулярность плоскостей
1.
Углы в пространстве. Перпендикулярность плоскостей.2.
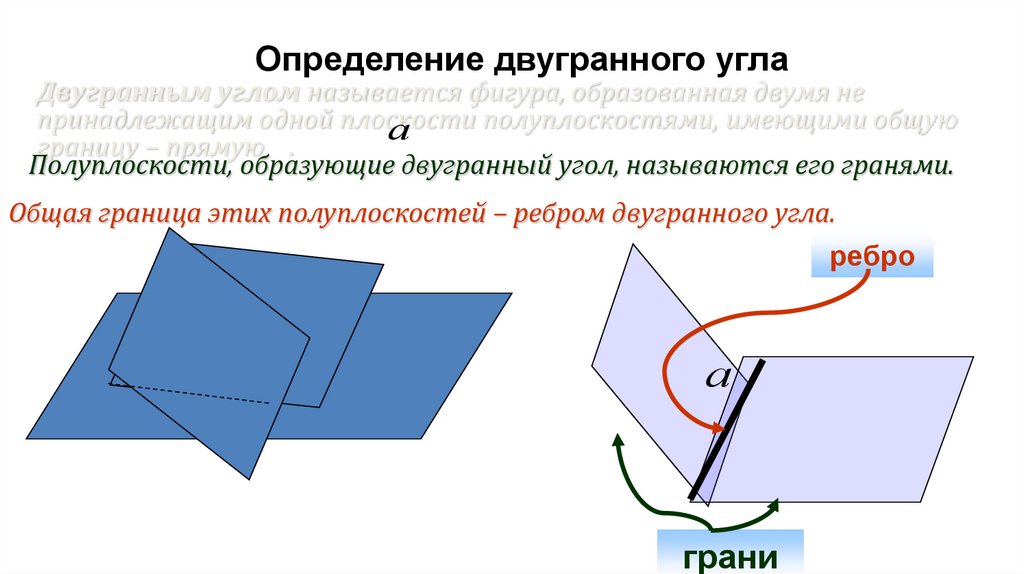
Определение двугранного углаДвугранным углом называется фигура, образованная двумя не
принадлежащим одной плоскости
полуплоскостями, имеющими общую
а
границу – прямую .
Полуплоскости, образующие двугранный угол, называются его гранями.
Общая граница этих полуплоскостей – ребром двугранного угла.
ребро
а
грани
3. Обозначение двугранного угла.
СD
В
А
Угол CBDA
4.
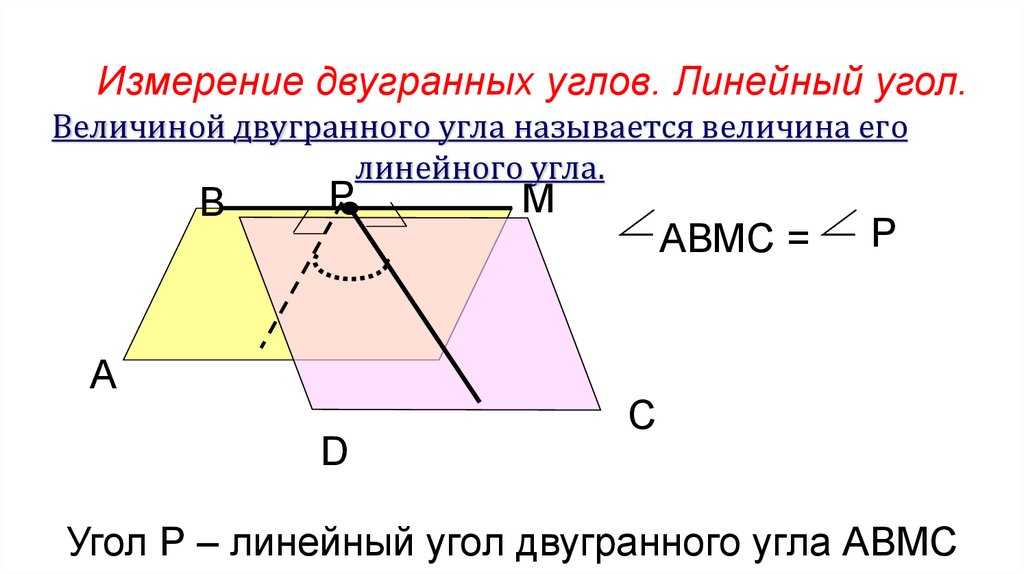
Измерение двугранных углов. Линейный угол.Величиной двугранного угла называется величина его
линейного угла.
В
Р
А
D
М
АВМС = Р
С
Угол Р – линейный угол двугранного угла АВМС
5.
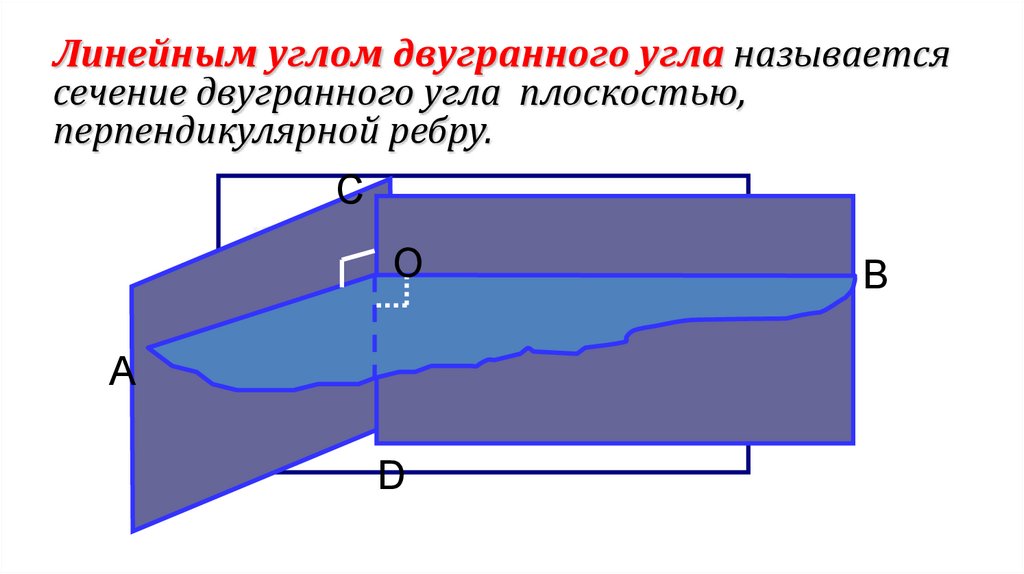
Линейным углом двугранного угла называетсясечение двугранного угла плоскостью,
перпендикулярной ребру.
С
О
А
D
В
6.
Способ нахождения (построения) линейного угла.1. Найти ( увидеть) ребро и грани двугранного
угла
2. В гранях найти направления ( прямые)
перпендикулярные ребру
3. (при необходимости) заменить выбранные
направления параллельными им лучами с общим
началом на ребре двугранного угла
При изображении сохраняется параллельность и
7.
Величина линейного угла не зависит от выбора еговершины на ребре двугранного угла.
B1
A1
A
O1
O
B
8.
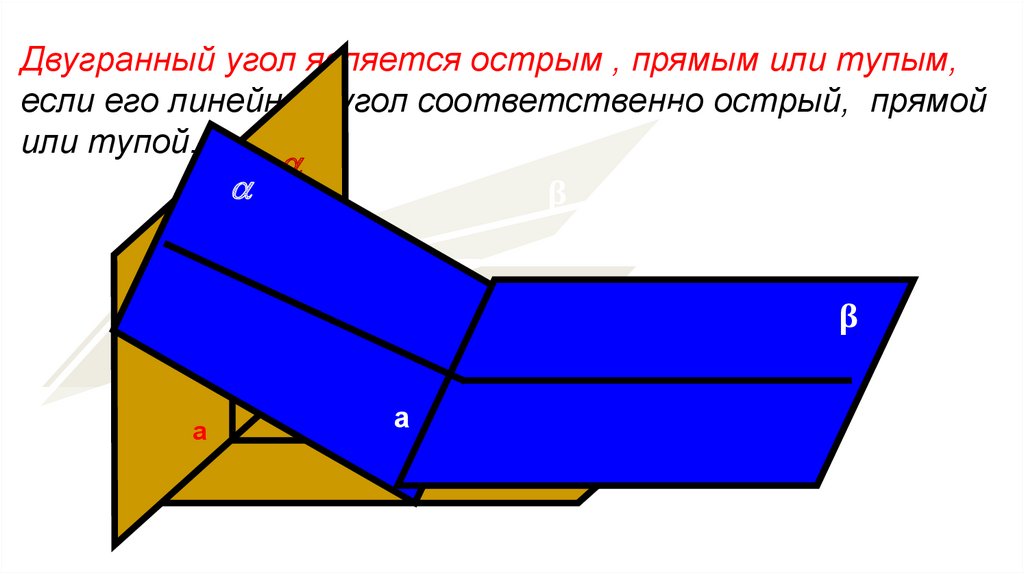
Двугранный угол является острым , прямым или тупым,если его линейный угол соответственно острый, прямой
или тупой.
β
β
а
а
β
9.
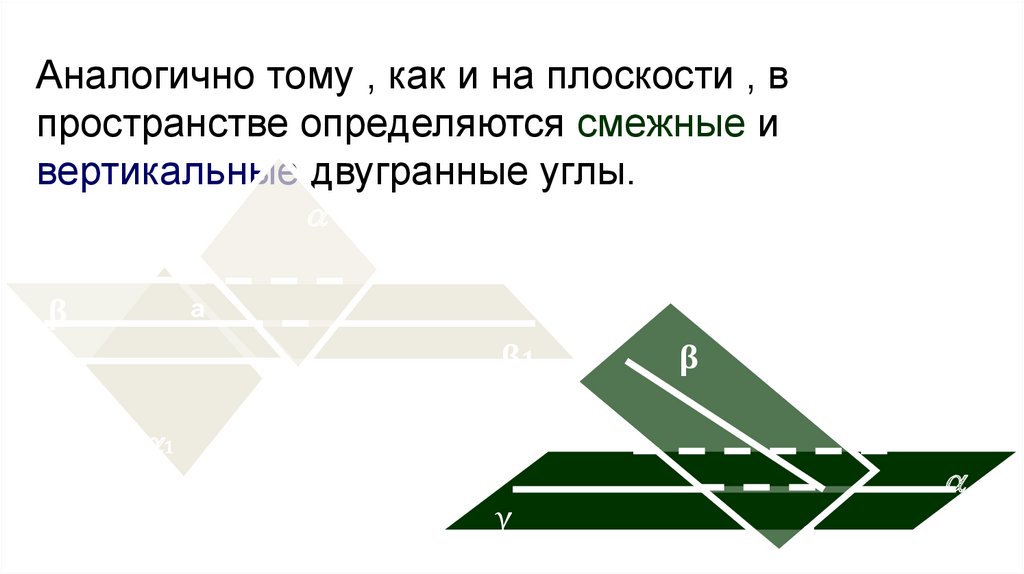
Аналогично тому , как и на плоскости , впространстве определяются смежные и
вертикальные двугранные углы.
β
а
β1
β
1
γ
а
10.
Углом между двумя пересекающимисяплоскостями называется наименьший из
двугранных углов, образованных при их
пересечении.
Угол между параллельными или совпадающими
плоскостями полагается равным нулю.
11.
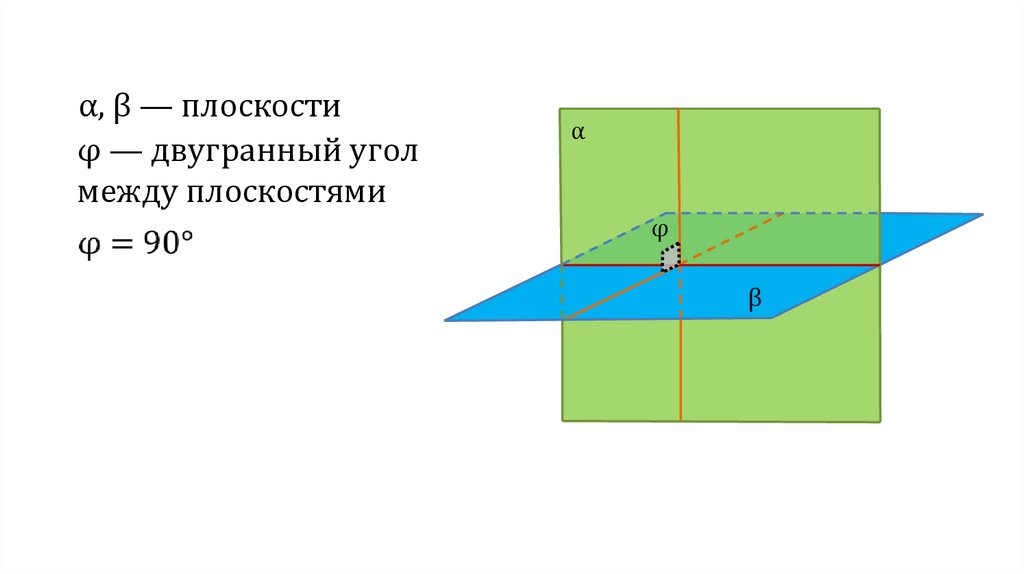
α, β — плоскостиφ — двугранный угол
между плоскостями
α
φ
β
12.
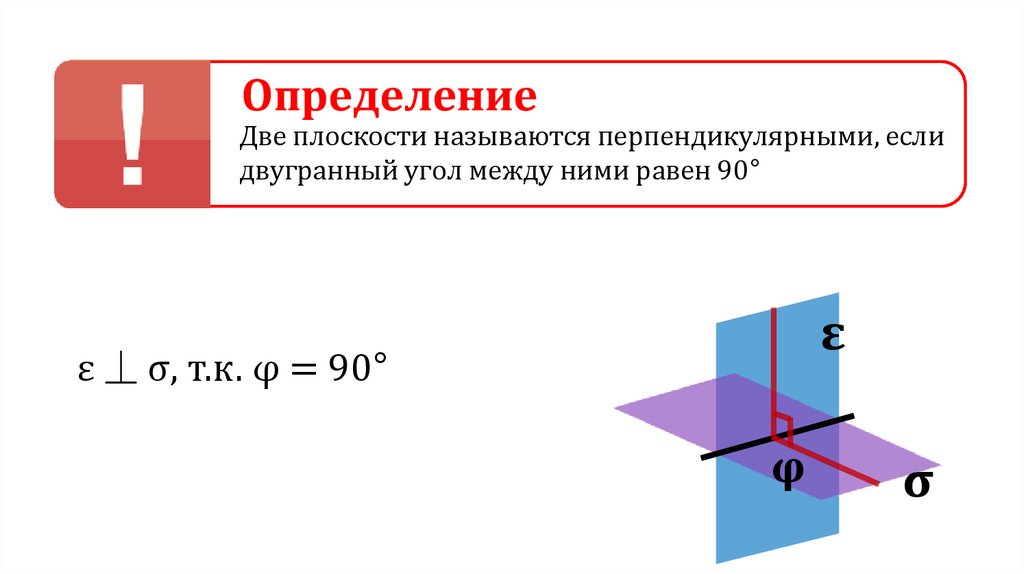
ОпределениеДве плоскости называются перпендикулярными, если
двугранный угол между ними равен 90°
ε
ε ⏊ σ, т.к. φ = 90°
φ
σ
13.
Стена и потолок14.
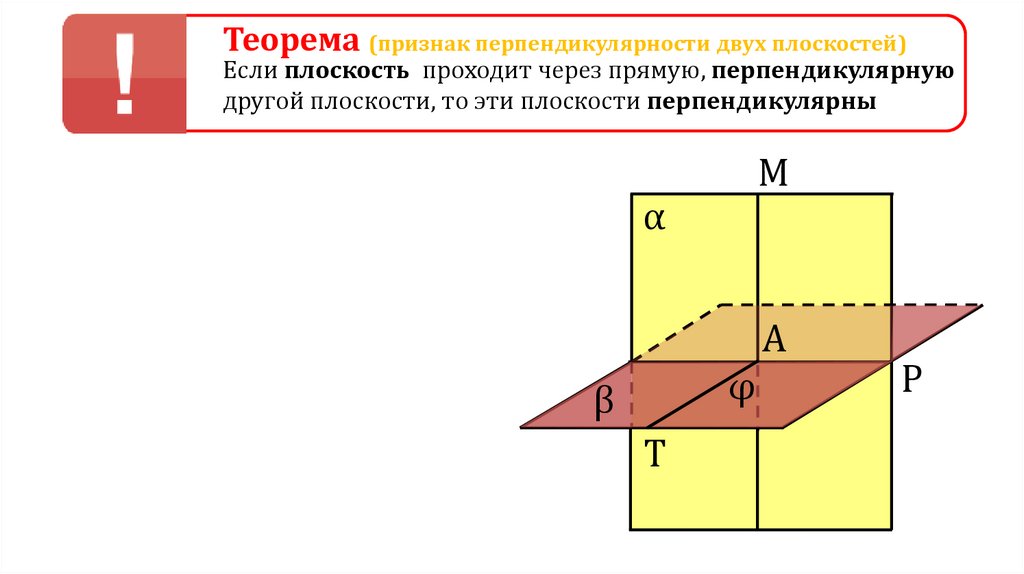
Теорема (признак перпендикулярности двух плоскостей)Если плоскость проходит через прямую, перпендикулярную
другой плоскости, то эти плоскости перпендикулярны
M
α
A
φ
β
T
P
15.
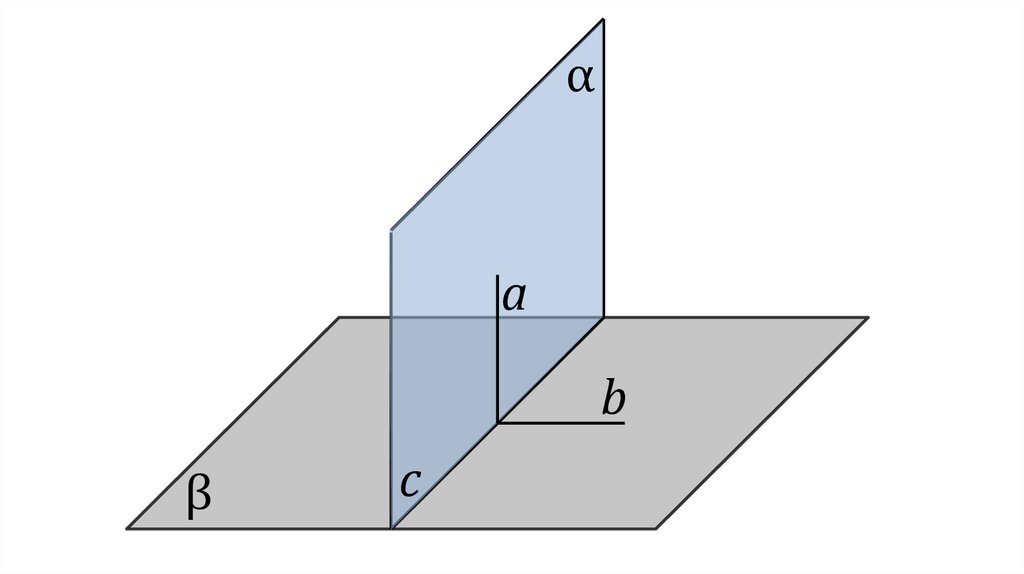
αa
b
β
c
16.
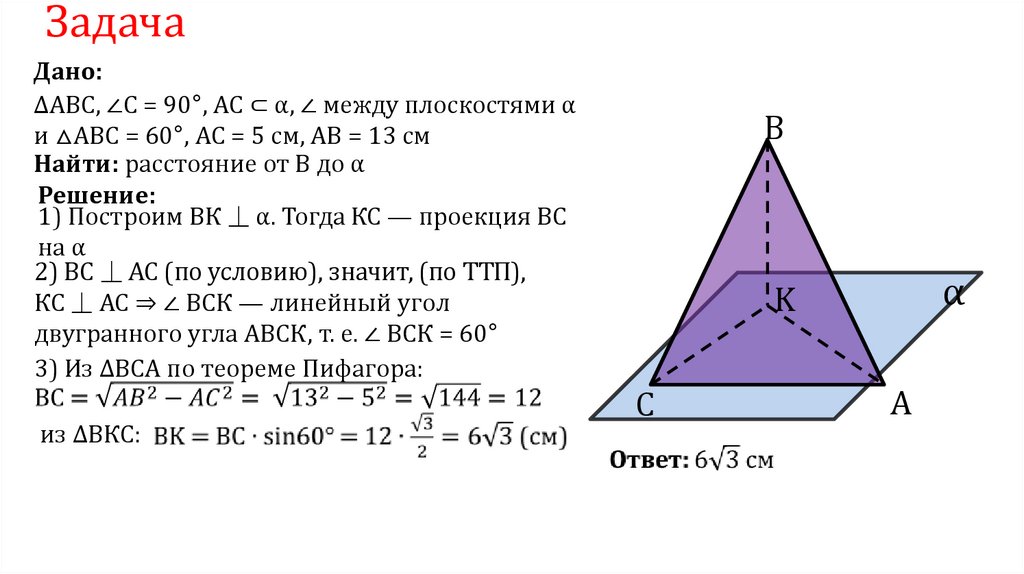
ЗадачаДано:
ΔАВС, ∠С = 90°, АС ⊂ α, ∠ между плоскостями α
и △ABC = 60°, АС = 5 см, АВ = 13 см
Найти: расстояние от В до α
Решение:
1) Построим ВК ⏊ α. Тогда КС — проекция ВС
на α
2) ВС ⏊ АС (по условию), значит, (по ТТП),
КС ⏊ АС ⇒ ∠ ВСК — линейный угол
двугранного угла АВСК, т. е. ∠ ВСК = 60°
3) Из ΔBCA по теореме Пифагора:
из ΔВКС:
B
α
K
C
A









 mathematics
mathematics








