Similar presentations:
Ряды динамики
1. Ряды динамики
РЯДЫ ДИНАМИКИ2.
Ряды динамики (временные ряды)применяются для изучения
изменения явлений во времени. Ряд
динамики представляет собой ряд
числовых значений определенного
статистического показателя в
последовательные моменты или
периоды времени
3. Ряд динамики
РЯД ДИНАМИКИпоследовательность
изменяющихся во времени
значений статистического
показателя , расположенного в
хронологическом порядке
4.
Составными элементами рядадинамики являются показатели
уровней ряда и периоды времени
(годы , кварталы , сутки) или
моменты (даты) времени. Уровни
ряда обычно обозначаются через
«y» , моменты или периоды
времени , к которым относятся
уровни – через «t»
5.
Примерt
yi
2006
15
2007
17
2008
18,5
2009
19
2010
21
Здесь t – время;
yi – производство продукции, тыс. шт.
6.
Взависимости от способа
выражения уровней ряда ряды
динамики делятся на ряды :
абсолютных
относительных
средних величин
7.
Взависимости от того , как выражают
уровни ряда (на начало месяца или за
период),выделяют моментные и
интервальные ряды динамики
В зависимости от расстояния между
уровнями ряды динамики бывают с
равностоящими и неравностоящими
уровнями во времени
В зависимости от наличия основной
тенденции изучаемого процесса ряды
динамики подразделяются на
стационарные и нестационарные
8.
Ряды динамики подразделяются намоментные и интервальные.
Моментным называется ряд,
абсолютные уровни которого
характеризуют величину явления по
состоянию на определенные моменты
времени или даты. (Например,
численность населения, уровни
товарных остатков)
9.
Интервальным называется такой ряд,абсолютные уровни которого
представляют собой итоговые величины за
некоторые интервалы времени (например,
производство продукции за месяц; число
родившихся за месяц, год).
Особенностью интервальных рядов является то,
что их уровни можно дробить и складывать
10.
Выделяют также производные рядыдинамики, которые состоят из средних
или относительных величин. Они
рассчитываются на основе моментных
или интервальных рядов. (Например,
среднегодовая численность населения)
11.
Основные показатели,применяемые для анализа рядов
динамики
12.
Анализ скорости и интенсивностиявления во времени
осуществляется с помощью
статистических показателей , которые
получаются в результате сравнения
уровней между собой . Сравниваемый
уровень называют отчётным , а
уровень , с которым происходит
сравнение – базисным
13.
Различают показатели измененияуровней ряда и средние
характеристики рядов динамики
14.
Ряды динамикиАбсолютные
величины
Относительны
е величины
Средние
величины
Интервальные
Интервальные
и Моментные
15.
К показателям изменения уровнейряда относятся абсолютный
прирост, коэффициент роста и
прироста, темп роста и
прироста, абсолютное
значение 1% прироста (роста)
16.
1.Абсолютные приросты бываютцепными и базисными. Абсолютный
прирост показывает, на сколько
изменился изучаемый показатель по
сравнению с предыдущим или базисным
периодом времени
17.
Базисный абсолютныйприрост:
ΔБ Yi Y0 ,
где y 0 - базисный уровень ряда
18.
Цепной абсолютныйприрост:
Δц Yi Yi 1 ,
где Yi - текущий уровень ряда;
Yi 1 - предыдущий уровень
ряда
19.
Годyi D ц Δ б k
ц
P
k
б
P
ц
р
б
р
ц
пр
%
б
пр
2006
15
-
0
-
1
-
100
-
0
-
17
2
2
1,133
1,133
113,3
113,3
13,3
13,3
0,150
18,5
1,5
3,5
1,088
1,233
108,8
123,3
8,8
23,3
0,170
19
0,5
4
1,027
1,266
102,7
126,6
2,7
26,6
0,185
21
2
6
1,105
1,400
110,5
140,0
10,5
40,0
0,190
2007
2008
2009
2010
ц
20.
2. Коэффициент ростапоказывает, во сколько раз изменился
изучаемый показатель по сравнению
с предыдущим периодом времени
или с базисным периодом времени.
Соответственно коэффициент роста
может быть цепным и базисным
21.
Цепной коэффициентроста:
K
ц
Pi
y
i
yi-1
22.
Базисный коэффициентроста:
yi
K
y0
б
Pi
23.
3.Темпы роста – этокоэффициенты роста, выраженные в
процентах (они также могут быть
цепными, базисными и средними):
Tр= Kp • 100 (%)
24.
Темп роста:а) базисный:
Tp
y / y *100
i
0
б) цепной :
Tp
y/y
i
i 1
100
25.
4.Темп прироста используется длявыражения величины абсолютного
прироста уровней ряда динамики в
относительных величинах:
100
T np T p
26.
Темп прироста показывает, насколько процентов изменился
изучаемый показатель по сравнению
с предыдущим периодом времени
или с базисным периодом времени.
Цепной темп прироста:
Yi Yi 1
ц
ц
Т прi
100 Т pi 100
yi-1
27.
Базисный темп приростаТ
б
ПРi
Yi Y 0
б
100 Т pt 100
y0
28.
5.Абсолютное значение одногопроцента прироста А% показывает,
сколько абсолютных единиц
содержится в 1% прироста
29.
Содержание одного процентабазисного прироста:
Δ
yt y 0
y0
А%
yt y 0
T
100
100
y0
б
t
б
t
б
прt
15
0 ,15
100
30.
Содержание одного процентацепного прироста:
Δ
yt yt 1
yt 1
А%
yt yt 1
T
100
100
yt 1
ц
t
ц
t
ц
прt
31.
Годyi D ц Δ б k
ц
P
k
б
P
ц
р
б
р
ц
пр
%
б
пр
2005
15
-
0
-
1
-
100
-
0
-
17
2
2
1,133
1,133
113,3
113,3
13,3
13,3
0,150
18,5
1,5
3,5
1,088
1,233
108,8
123,3
8,8
23,3
0,170
19
0,5
4
1,027
1,266
102,7
126,6
2,7
26,6
0,185
21
2
6
1,105
1,400
110,5
140,0
10,5
40,0
0,190
2006
2007
2008
2010
ц
32.
Расчет среднего уровняряда динамики
33. средние характеристики ряда
СРЕДНИЕ ХАРАКТЕРИСТИКИ РЯДАСредний уровень ряда динамики
рассчитывается по формулам
средней арифметической или
средней хронологической
34.
1.Еслиряд
динамики
является
интервальным, то расчет среднего
уровня ведется по формуле простой
средней арифметической:
Y
Y
i
n
35. Средний уровень ряда
СРЕДНИЙ УРОВЕНЬ РЯДАДЛЯ ИНТЕРВАЛЬНЫХ РЯДОВ
С РАВНЫМИ ИНТЕРВАЛАМИ ВРЕМЕНИ
Простая средняя арифметическая
y
/
n
y
=
i
где n - количество периодов времени
36.
Пример. Имеются следующие данные о динамикепроизводства продукции предприятием за 20062010 гг., тыс. шт.
2006 г.
2007 г.
2008 г.
2009 г.
2010 г.
205
213
222
229
236
Определить
среднегодовое
продукции за 2006-2010 гг.
производство
205 213 222 229 236 1105
Y
221
5
5
тыс. шт.
37.
2. Если ряд динамики является моментным сразличными интервалами времени между датами, то
для расчета среднего уровня используется средняя
арифметическая взвешенная:
t
где i – продолжительность i-го интервала времени
(интервал времени между двумя соседними
значениями;
Yi - средний уровень ряда для i-го интервала
времени
38.
Пример. Известна списочная численностьперсонала организации по состоянию на
следующие даты (человек) :
01.01
01.03
01.06
01.09
01.01
след.год
1200
1100
1250
1500
1350
Среднесписочная численность персонала за
год составляет:
1200 1100
1100 1250
1250 1500
1500 1350
2
3
3
4
2
2
2
2
у
12
31300
1304 чел.
24
39.
С неравными интервалами времениЭта формула иногда дается как взвешенная
средняя хронологическая
y
=
y y t / 2 t
i
i 1
i
где ti – период времени между двумя
соседними значениями
i
40.
3.Если ряд динамики является моментным сравноотстоящими уровнями, то используется
средняя хронологическая простая:
y1
yn
y 2 y3 ... y n-1
2 ,
y 2
n 1
где n-количество дат
41.
Пример. Известны товарные остаткимагазина на 1-е число каждого месяца
(тыс. руб.) :
01.01
01.02
01.03
01.04
180
140
160
200
Средний уровень товарных остатков за
первый квартал составил:
180
200
140 160
2 163
у 2
3
тыс. руб.
42.
Среднийабсолютный прирост
определяется как простая средняя
арифметическая величина из
цепных абсолютных приростов и
показывает , на сколько в
среднем изменялся показатель в
течение изучаемого периода
времени
43.
Средний абсолютный приростпоказывает, на сколько в среднем изменялся
изучаемый показатель при переходе от
предыдущего периода времени к смежному
последующему периоду времени
ΣΔi Σ(Yi Yi 1 ) Yn Y 1
Δ
,
s
s
n 1
где
n – число уровней ряда динамики;
S = n - 1 – количество цепных приростов
44.
2 1,5 0,5 2Δ
1,5
5 1
21 15
Δ
1,5
5 1
45.
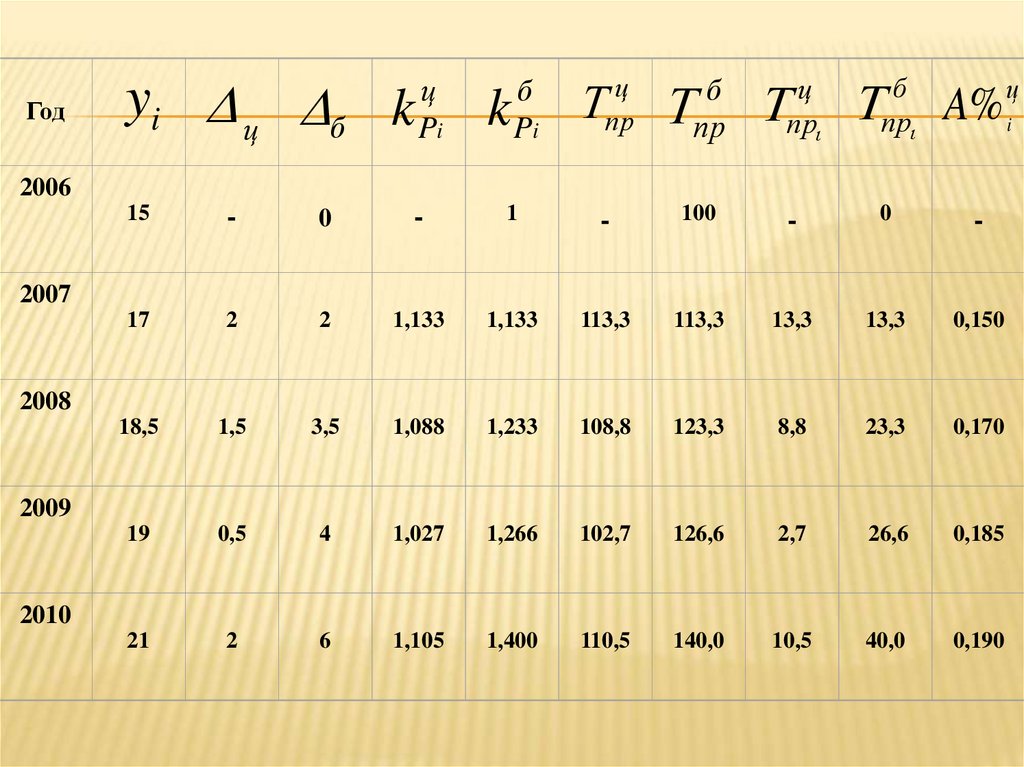
Годyi D ц Dб k Pц k Pб прц прб прц прб A% ц
i
i
i
2006
15
-
0
-
1
-
100
-
0
-
17
2
2
1,133
1,133
113,3
113,3
13,3
13,3
0,150
18,5
1,5
3,5
1,088
1,233
108,8
123,3
8,8
23,3
0,170
19
0,5
4
1,027
1,266
102,7
126,6
2,7
26,6
0,185
21
2
6
1,105
1,400
110,5
140,0
10,5
40,0
0,190
2007
2008
2009
2010
46.
Среднегодовойкоэффициент
роста определяется как средняя
геометрическая из цепных
коэффициентов роста и
показывает , сколько в среднем
составлял рост показателя
47.
Еслицепные коэффициенты роста
определялись для рядов с
равностоящими интервалами, то
применяется простая средняя
геометрическая величина
48.
Средний коэффициентроста рассчитывается по формуле
средней геометрической из цепных
коэффициентов роста:
k
n 1
ц
ц
ц
2
3
4
k k k
ц
... k n
k 5 1 1,133 1,088 1,027 1,105 1,088
49.
k n 1k b a
yn
21
4
1,088
y1
15
y b 2008 2004 21
1,088
ya
15
50.
Годyi D ц Dб k Pц k Pб прц прб Tпрц Tпрб A% ц
i
i
i
i
i
2006
15
-
0
-
1
-
100
-
0
-
17
2
2
1,133
1,133
113,3
113,3
13,3
13,3
0,150
18,5
1,5
3,5
1,088
1,233
108,8
123,3
8,8
23,3
0,170
19
0,5
4
1,027
1,266
102,7
126,6
2,7
26,6
0,185
21
2
6
1,105
1,400
110,5
140,0
10,5
40,0
0,190
2007
2008
2009
2010
51.
С неравными интерваламивремени
Взвешенная средняя геометрическая
t
k =
i
t1
t2
t1
1n
k1 *k 2 *k 3 *...*k n
где ki – коэффицент роста;
ti – период времени между двумя
соседними значениями
52.
Среднегодовойтемп роста
определяется умножением
среднегодового коэффициента
роста на 100 и показывает ,
сколько процентов в среднем
составлял рост показателя
53. Средний темп прироста
СРЕДНИЙ ТЕМП ПРИРОСТАПоказывает, на сколько процентов
увеличивается (или уменьшается)
уровень по сравнению с предыдущем в
среднем за единицу времени:
Т пр Т р 100
54.
Т пр 108,8% 100% 8,8%55.
Проблема сопоставимостиуровней рядов динамики
Смыкание рядов динамики
56.
Поскольку ряды динамикиформируются на протяжении
длительных периодов времени, их
уровни часто оказываются
несопоставимыми
57.
Причины1. Изменение цен
2. Изменение методики расчета
показателей
3. Изменение «границ» (организационных, административных)
58.
Для обеспечения сопоставимости данныхчасто применяется метод смыкания рядов
динамики. Для смыкания ряда динамики
необходимо иметь переходное звено.
(Переходное звено – это период времени,
для которого изучаемый показатель
рассчитан как по старой методике (в старых
границах), так и по новой методике (в новых
границах).
Для переходного звена рассчитывается
коэффициент, действие которого
распространяется на все предшествующие
периоды времени
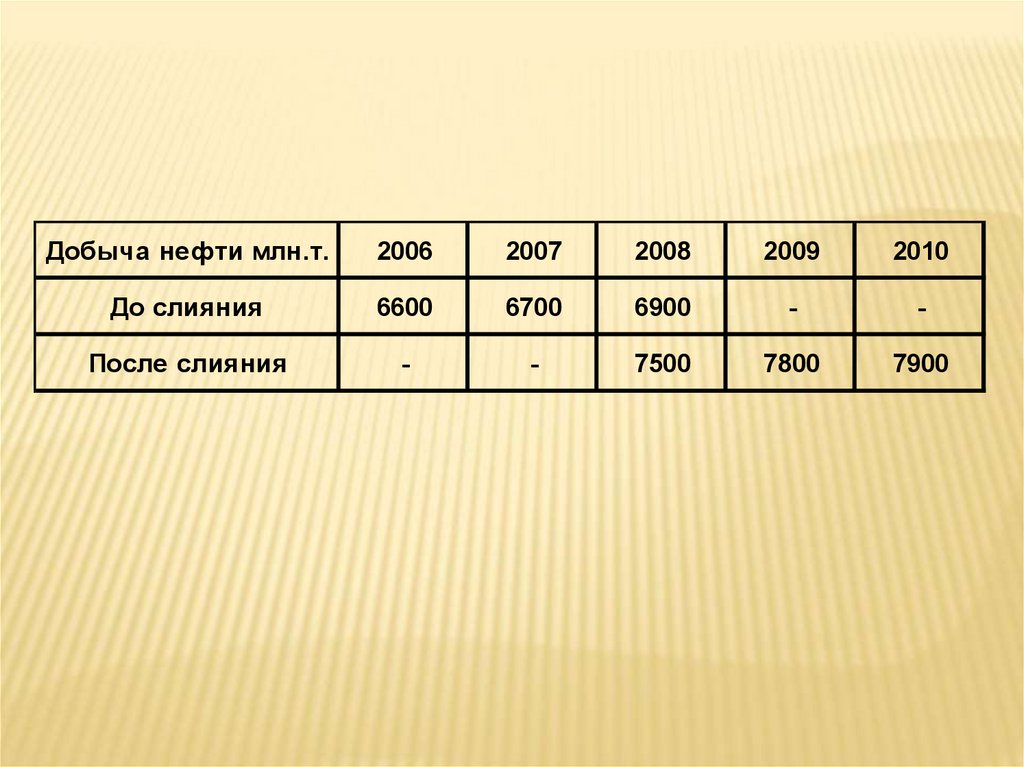
59.
Добыча нефти млн.т.2006
2007
2008
2009
2010
До слияния
6600
6700
6900
-
-
После слияния
-
-
7500
7800
7900
60.
7500К
1,087
6900
61.
y07 6700 1,087 7283y06 6600 1,087 7174
62.
Добыча нефти млн.т.2006
2007
2008
2009
2010
До слияния
6600
6700
6900
-
-
После слияния
-
-
7500
7800
7900
Сопоставимый ряд
7174
7283
7500
7800
7900
63.
Анализ основной тенденциирядов динамики
64.
Уровни рядов динамикиформируются под воздействием
большого числа факторов. Их
можно разделить на 3 группы
65.
1. Определяющие факторы –факторы, которые оказывают
постоянное и сильное воздействие на
изучаемый показатель. Они
определяют основную тенденцию
(тренд) ряда динамики
66.
67.
2. Сезонные факторы – факторы,которые вызывают сезонные
колебания относительно основной
тенденции
68.
69.
3. Случайные факторы – факторы,которые вызывают случайные
колебания уровней ряда (например,
погодный фактор)
70.
Метод укрупненияинтервалов
71.
Метод укрупненияинтервалов – замена исходных
уровней ряда средними
величинами, которые
рассчитываются для
укрупненных интервалов
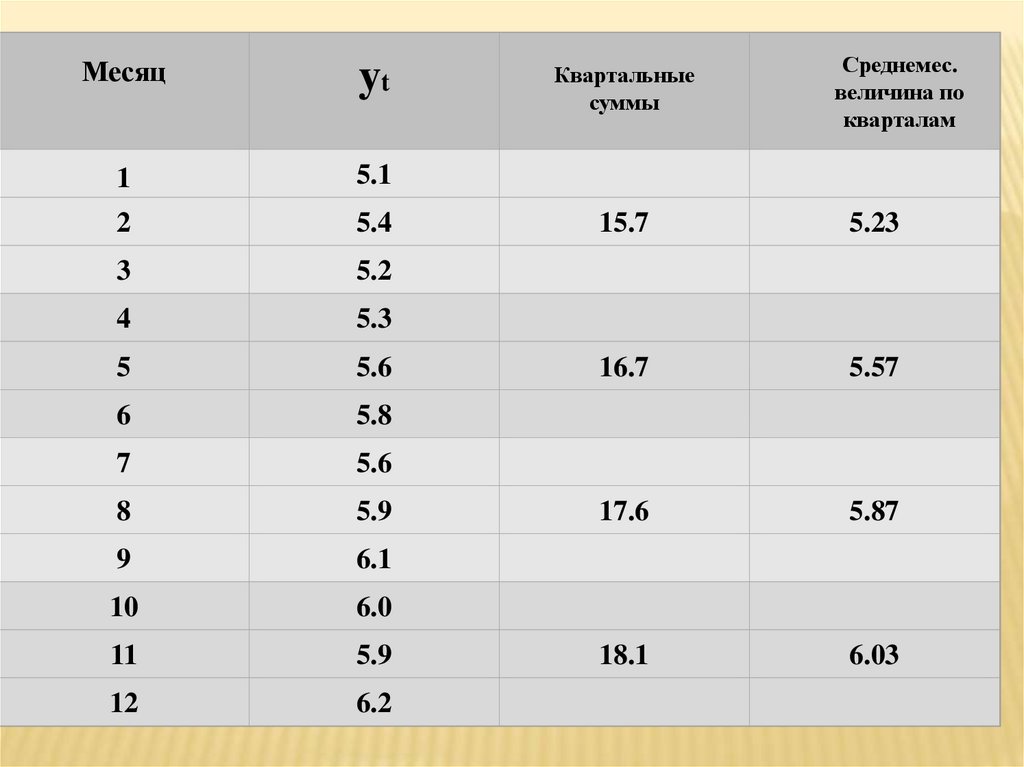
72.
Месяцyt
1
5.1
2
5.4
3
5.2
4
5.3
5
5.6
6
5.8
7
5.6
8
5.9
9
6.1
10
6.0
11
5.9
12
6.2
Квартальные
суммы
Среднемес.
величина по
кварталам
15.7
5.23
16.7
5.57
17.6
5.87
18.1
6.03
73.
Метод скользящейсредней
74.
Метод скользящейсредней– замена исходных
уровней ряда средними
величинами, которые
рассчитываются для
последовательно смещающихся
интервалов времени
75.
Год2002
2003
2004
2005
2006
2007
2008
2009
2010
yt
4.5
4.3
5.2
5.3
5.7
6
6
5.9
5.7
ЧетырехПятичленная скользящая членная
скользящ.
сумма
средняя
сумма
25
26.5
28.2
28.9
29.3
-
5
5.3
5.64
5.78
5.86
-
19,3
20,5
22,2
23
23,6
23,6
Центрированная
скользящая
сумма
средняя
-
-
-
-
19.9
21.35
22.6
23.3
23.6
4.98
5.34
5.65
5.83
5.9
-
-
-
-
76.
Аналитическоевыравнивание рядов
динамики
77.
Уровни ряда рассматриваютсякак некоторая функция от
времени:
y t f(t)
78.
Процедура выравнивания в этомслучае сводится:
к выбору вида функции;
к определению параметров функции;
к получению выравненных значений
уровней ряда на
основе функции
79.
Рассмотрим данный метод напримере линейного уравнения
(тренда):
Λ
y t a b t,
где a и b – параметры;
t – время
80.
Линейный тренд лучше всегоиспользовать в тех случаях, когда
предварительный анализ показывает,
что уровни ряда изменяются с
примерно одинаковой скоростью, т.е.
когда цепные абсолютные приросты
примерно равны между собой
81.
Параметры a и b определяютсяпри помощи метода наименьших
квадратов (МНК)
82.
Применение метода МНК даетследующую систему уравнений для
определения параметров:
a t b t (y t t)
2
a n b t yt
83.
Данную систему уравненийможно существенно упростить,
если пронумеровать время таким
образом, чтобы
t 0
84.
Если ряд содержит нечетное числоуровней, то центральный уровень
ряда нумеруется нулем. Уровни в
сторону убывания времени
нумеруются -1; -2; -3…, в сторону
возрастания времени 1; 2; 3…
85.
Если ряд содержит четное числоуровней, то ближайшие к центру
уровни ряда нумеруются: -1 и 1,
далее нумерация как для ряда с
нечетным числом уровней только с
шагом 2: …-5; -3; -1; +1; +3; +5…
86.
a n ytb t (y t t)
2
y
a
t
n
(y t)
b
t
t
2
87.
ΛΛ
Год
y t Δ t t y t t y (y t y t )
t
2006
800
2007
ц
t
-2
4
857 57
-1
1
-857
857.7
0.49
2008
915 58
0
0
0
917.2
4.84
2009
976 61
1
1
976
976.7
0.49
2010 1038 62
2
4
2076 1036.2
3.24
0
10
Итого: 4586
-
2
-
-1600 798.2
595
4586.0
0.24
12.3
2
88.
4586a
917,2
5
595
b
59,5
10
Λ
y t 917,2 59,5 t
89.
цt
t t 2 yt t
-
-2
4
Λ
Λ
y t (y t y t )
Год
yt Δ
2006
800
2007
857 57
-1
1
-857
857.7
0.49
2008
915 58
0
0
0
917.2
4.84
2009
976 61
1
1
976
976.7
0.49
2010 1038 62
2
4
2076 1036.2
3.24
0
10
Итого: 4586
-
-1600 798.2
595
4586.0
0.24
12.3
2
90.
Выравнивание по параболе второгопорядка:
Λ
y a b t c t ,
2
где b – скорость изменения уровней
ряда динамики
c – ускорение
91.
Выравнивание по параболе второгопорядка производится, когда
предварительный анализ показывает, что
вторые разности примерно равны между
собой
(1)
Δ t y t y t 1 - первая разность;
Δ
(2)
t
Δ Δ
(1)
t
(1)
t 1
- вторая разность
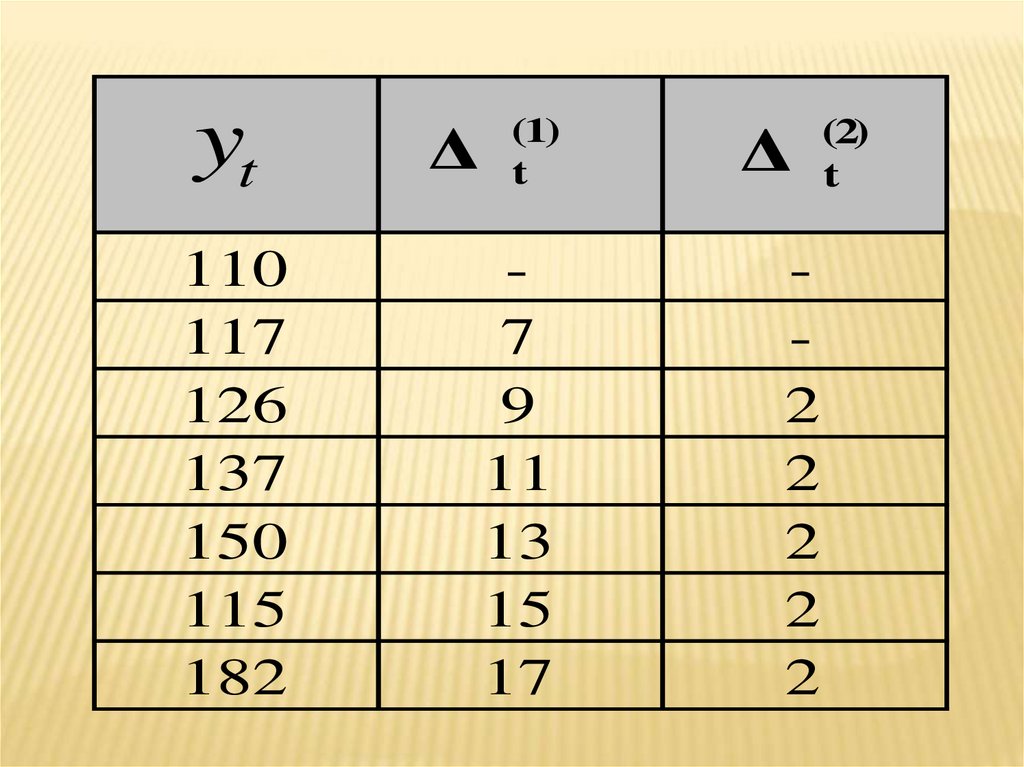
92.
yt110
117
126
137
150
115
182
Δ
(1)
t
7
9
11
13
15
17
Δ
2
2
2
2
2
(2)
t
93.
Для определения параметровприменяется метод наименьших
квадратов:
a n b t c t yt
2
a t b t c t (y t t)
2
3
a t b t c t (y t t )
2
3
4
2
94.
Выравнивание по гиперболеприменяется в тех случаях, когда в
развитии ряда динамики происходит
насыщение
Λ
b
y a
t
95.
96.
Для определения параметровиспользуется МНК:
1
a n b yt
t
yt
1
1
a b 2
t
t
t
97.
Выравнивание ряда динамики при помощипоказательных функций или экспоненты
применяется, когда предварительный анализ
показывает: уровень ряда динамики меняется с
приблизительно одинаковыми цепными
коэффициентами роста. При этом коэффициент
b интерпретируется как средний коэффициент
роста
Λ
yt a b
t
98.
Для определения параметров функцияприводится предварительно к линейному
виду при помощи логарифмирования
левой и правой частей уравнения
Λ
lg y lga t lgb
При этом мы находим не a и b,
а lga и lgb
99.
n lga t lgb lgy tt lga t
2
lgb (lgy t t)











































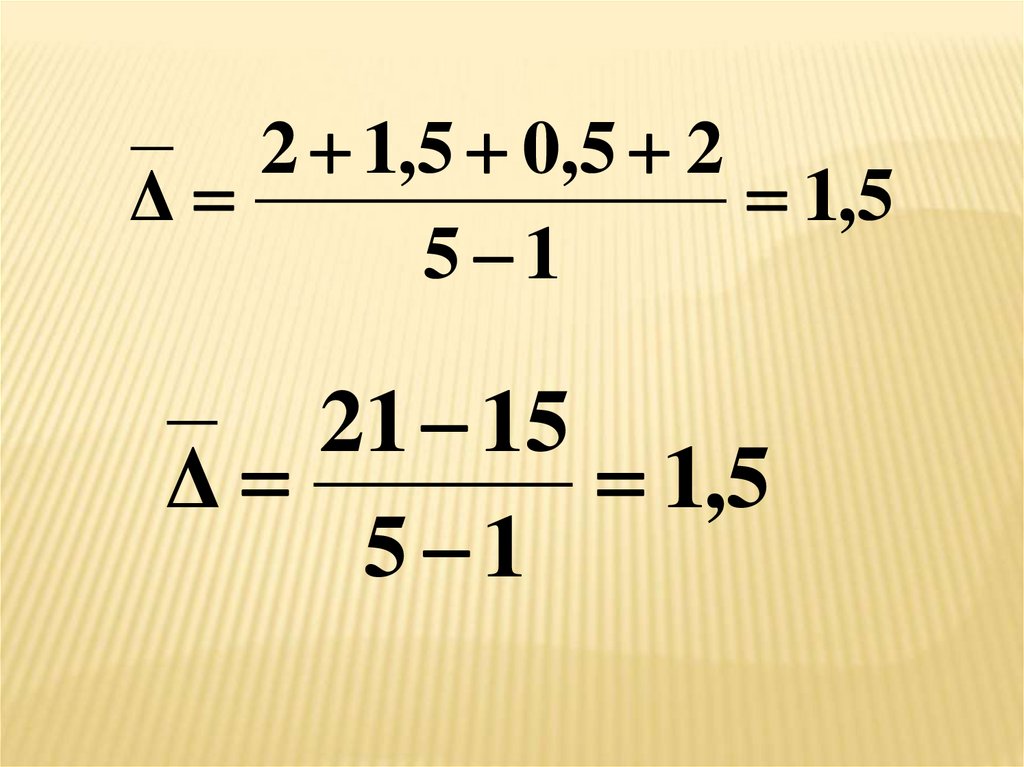



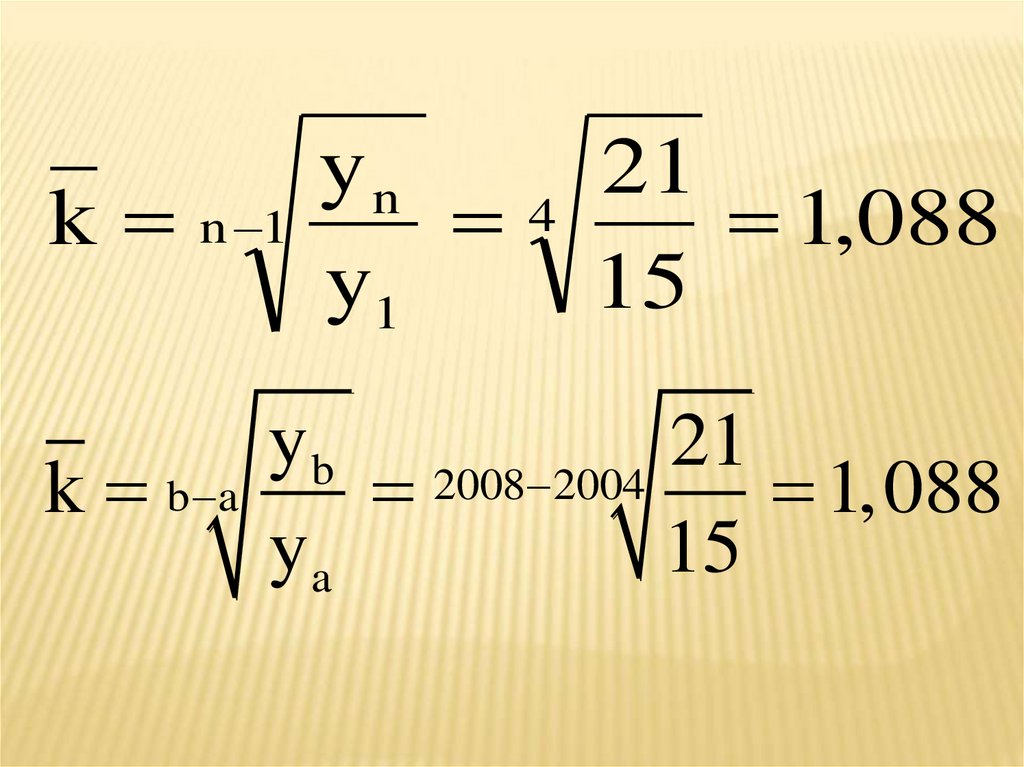

































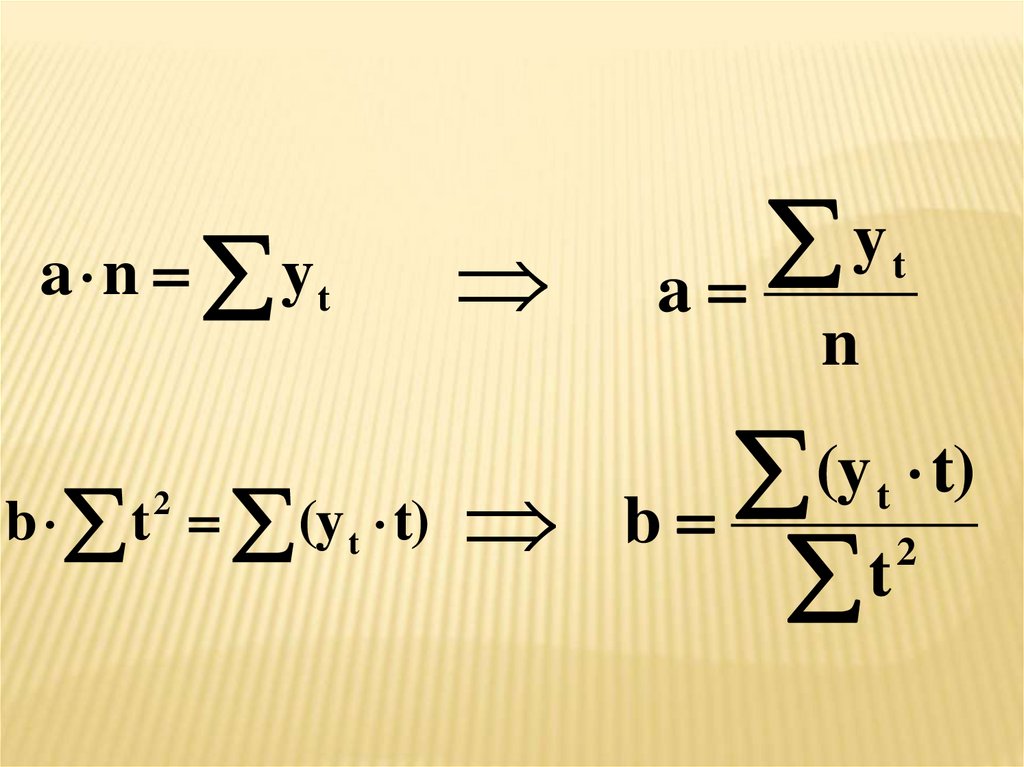

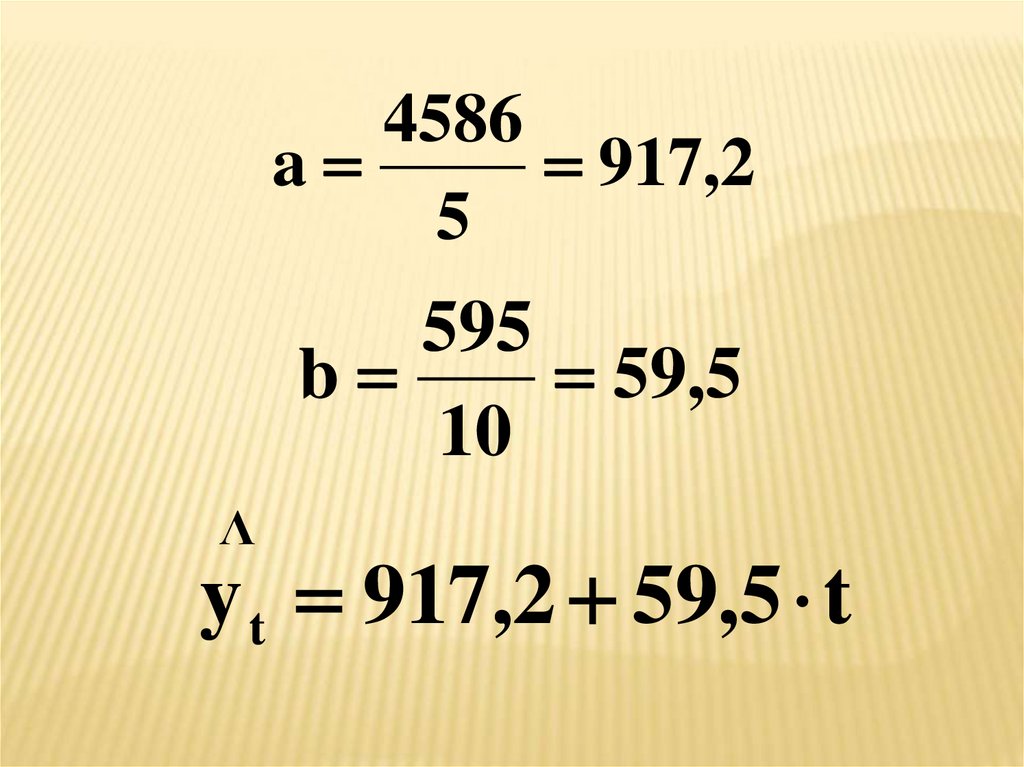










 mathematics
mathematics








