Similar presentations:
Ряды динамики. Статистика
1. Тема . Ряды динамики
ТЕМА . РЯДЫ ДИНАМИКИ1.
2.
3.
4.
5.
6.
7.
Динамический ряд, его элементы, виды и
правила построения
Смыкание рядов динамики. Приведение
рядов динамики к одному или общему
основанию
Расчет аналитических показателей в
рядах динамики
Средние показатели ряда динамики
Методы выявления основной тенденции
развития в рядах динамики.
Изучение сезонных колебаний в рядах
динамики
Статистические методы моделирования
и
прогнозирования
социальноэкономических явлений
1
2.
1. Процесс развития, движения социальноэкономическихявлений
во
времени
в
статистике принято называть динамикой.
Ряд динамики или временной ряд – это
совокупность значений показателя, взятых за
ряд последовательных моментов или периодов
времени.
Ряд динамики содержит два показателя:
Показатель времени
t – это периоды времени
(годы, кварталы, месяцы, сутки) или моменты
(даты) времени;
Уровень ряда - y;
2
3.
1.2.
3.
Классификация рядов динамики:
В зависимости от способа выражения уровней
ряда, ряды динамики подразделяются на ряды
абсолютных, относительных и средних величин.
В зависимости от того, как выражают уровни
ряда
состояние явления на определенные
моменты времени (на начало месяца, квартала,
года и т. п.) или его величину за определенные
интервалы времени (например, за сутки, месяц,
год и т. п.), различают соответственно
моментные и интервальные ряды динамики.
В зависимости от расстояния между уровнями
ряды динамики подразделяются на ряды
динамики с равноотстоящими уровнями и
неравноотстоящими уровнями во времени.
3
4.
4. В зависимости от наличия основной тенденцииизучаемого
процесса
ряды
динамики
подразделяются
на
стационарные
и
нестационарные.
4
5.
2.Важнейшим
условием
правильного
построения
ряда
динамики
является
сопоставимость всех входящих в него уровней.
Данное условие решается либо в процессе сбора
и обработки данных, либо путем их пересчета.
Научный
подход к изучению рядов
динамики заключается в том, чтобы ряды,
охватывающие большие периоды времени,
разбивать на группы, которые бы объединяли
лишь однокачественные
периоды развития
совокупности,
характеризующейся
одной
закономерностью развития.
5
6.
Для того чтобы привести уровни рядадинамики
к
сопоставимому
виду,
иногда
приходится
прибегать
к
приему,
которым
называется «смыкание рядов динамики».
Под смыканием понимают объединение в
один ряд (более длинный) двух или нескольких
рядов динамики, уровни которых исчислены по
разной методологии или разным территориальным
границам.
6
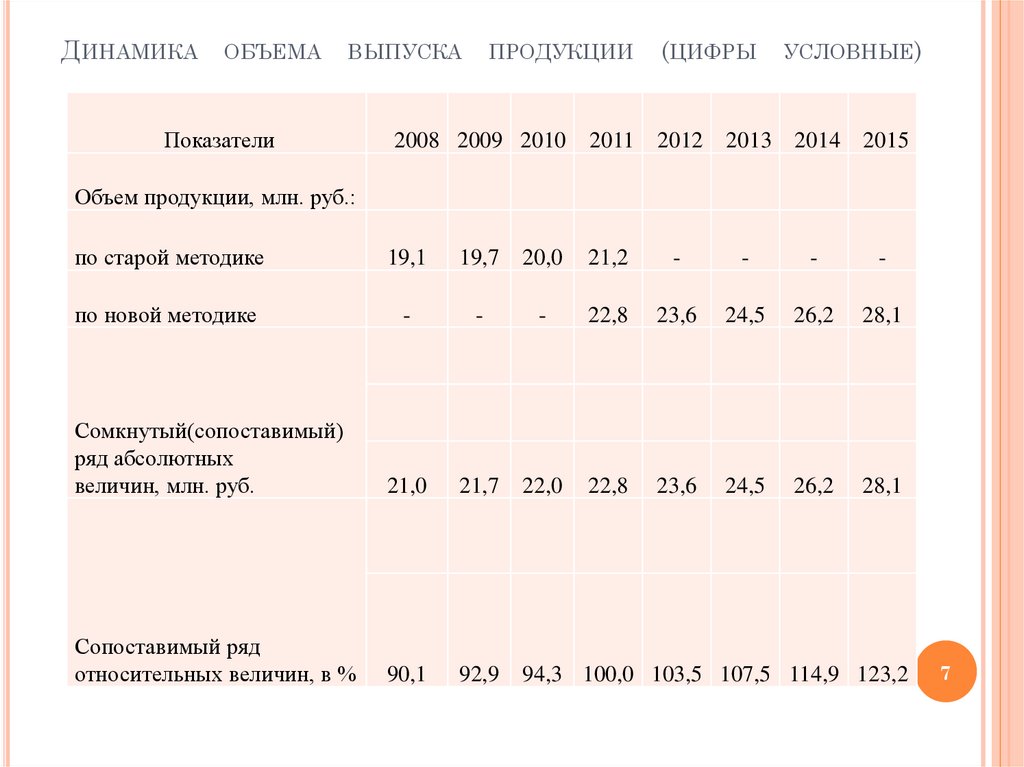
7. Динамика объема выпуска продукции (цифры условные)
ДИНАМИКАОБЪЕМА
ВЫПУСКА
Показатели
ПРОДУКЦИИ
2008 2009 2010
(ЦИФРЫ
2011 2012
УСЛОВНЫЕ)
2013 2014 2015
Объем продукции, млн. руб.:
по старой методике
19,1
19,7
20,0
21,2
-
-
-
-
по новой методике
-
-
-
22,8
23,6
24,5
26,2
28,1
Сомкнутый(сопоставимый)
ряд абсолютных
величин, млн. руб.
21,0
21,7
22,0
22,8
23,6
24,5
26,2
28,1
Сопоставимый ряд
относительных величин, в %
90,1
92,9
94,3 100,0 103,5 107,5 114,9 123,2
7
8.
Для анализа динамики объема выпуска продукцииза 2008-2015 гг. необходимо сомкнуть (объединить)
исследуемые два ряда в один. А чтобы уровни нового ряда
были сопоставимы, следует пересчитать данные 2008 2015 гг. по новой методике. Для этого, на основе данных
об объеме продукции за 2011 г. где имеются данные по
новой и старой методике, находим соотношение между
ними:
22,8 : 21,2 = 1,1. Умножая на полученный
коэффициент данные по старой методике за 2008-2010 гг.,
приводим их таким образом в сопоставимый вид с
последующими уровнями. Сомкнутый (сопоставимый) ряд
динамики показателей представлен в предпоследней
строке таблицы
8
9.
Другой способ смыкания рядов динамикизаключается в том, что уровни года, в котором
произошли изменения (в нашем примере уровни
2011 г.), как до изменений, так и после изменений
(в старой и новой методике, т. е. 21,2 и 22,8)
принимаются
за
100%,
а
остальные
пересчитываются в процентах по отношению к этим
уровням соответственно
(в старых ценах - по
отношению к 21,2, в новых ценах - к 22,8). В
результате получаем сомкнутый ряд динамики,
который показан в последней строке таблицы.
9
10.
Проблемаприведения
показателей
к
сопоставимому
виду
возникает
при
параллельном анализе развития во времени
экономических показателей отдельных стран,
административных и территориальных районов.
Это, во-первых, вопрос о сопоставимости цен
сравниваемых стран, во-вторых, о сопоставимости
методики расчета сравниваемых показателей. В
таких случаях ряды динамики приводятся к
одному основанию, т. е. к одному и тому же
периоду или моменту времени, уровень которого
принимается за базу сравнения, а все остальные
уровни выражаются в виде коэффициентов или в
процентах по отношению к нему.
10
11.
Пример. Имеются данные об экспорте товаровдвух стран, млн дол. США (табл.2). Различные
значения абсолютных уровней приведенных
рядов динамики затрудняют выявление
особенностей экспорта товаров в странах А и
Б. Поэтому приведем абсолютные уровни рядов
динамики к общему основанию, приняв за
постоянную базу сравнения уровни 2011 г.;
получим следующие данные (в % к 2011 г.,
табл. 2).
11
12. Таблица 2 Экспорт товаров стран за 2011-2015 гг., тыс. дол. США.
ТАБЛИЦА 2ЭКСПОРТ ТОВАРОВ СТРАН ЗА 2011-2015 ГГ., ТЫС.
ДОЛ. США.
2011
2012
2013
2014
2015
Страна А
45,5
72,4
95,2
122,0
128,0
Страна Б
56,1
65,1
66,5
65,0
67,0
12
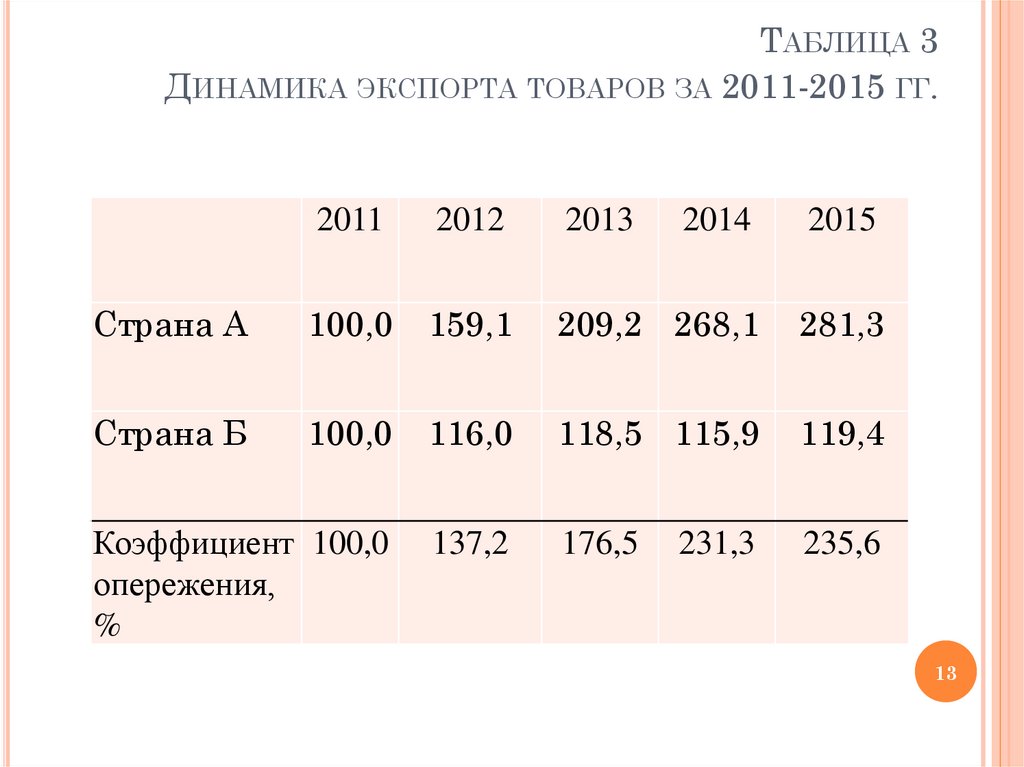
13. Таблица 3 Динамика экспорта товаров за 2011-2015 гг.
ТАБЛИЦА 3ДИНАМИКА ЭКСПОРТА ТОВАРОВ ЗА 2011-2015 ГГ.
2011
2012
2013
2014
2015
Страна А
100,0
159,1
209,2 268,1
281,3
Страна Б
100,0
116,0
118,5 115,9
119,4
Коэффициент 100,0
опережения,
%
137,2
176,5
235,6
231,3
13
14.
В относительных величинах, выраженных вбазисных темпах
роста по каждой стране,
несопоставимость уровней рядов динамики
нивелируется. Различный характер развития
явления выступает более наглядно.
Данный прием называется - приведение
рядов
динамики
к
одному
показателю
(основанию).
Интенсивность
развития
определяют
при
помощи
коэффициента
опережения как отношение базисных темпов
роста одного объекта к темпам роста другого
объекта.
Из данных таблицы 3 видно, что
производство цемента в стране А непрерывно и
быстро растает, значительно превосходя темпы
роста в стране Б, это видно также из расчетов
коэффициента опережения.
14
15.
3. Анализ скорости и интенсивности развитияявления во времени осуществляется с помощью
статистических показателей, которые получаются
в результате сравнения уровней между собой.
Различают аналитические и средние показатели
ряда динамики.
К аналитическим показателям относятся:
- абсолютный прирост (снижение);
- коэффициент роста;
- темп роста;
- темп прироста;
- абсолютное значение одного процента прироста
(снижения).
При этом принято сравниваемый уровень
называть отчетным, а уровень, с которым
производят сравнение - базисным.
15
16.
Введем условные обозначения:y1 - начальный уровень ряда динамики;
yn конечный уровень ряда динамики;
yi
уровень ряда динамики за i-й
период;
yi-1 - уровень ряда динамики предыдущего
периода;
y - средний уровень ряда;
y0
- уровень ряда, принятый за базу
сравнения.
16
17.
Ряды динамики подразделяются на:Ряды динамики абсолютных величин
Ряды динамики относительных величин
Ряды динамики средних величин
Основными для анализа являются ряды
динамики абсолютных величин, которые
бывают интервальные и моментные.
Интервальным называется ряд динамики, в
котором уровни ряда берутся за определенный
период времени.
Моментным называется ряд динамики, уровни
которого даны на определенный момент
времени.
17
18.
Абсолютный прирост характеризуетразмер (увеличения или уменьшения) уровня
ряда за определенный промежуток времени. Он
равен разности двух сравниваемых уровней и
выражает абсолютную скорость изменения.
Рассчитывается двумя способами;
уц yi yi 1
уб yi y0
цепной
базисный
18
19.
Интенсивность изменения уровня динамикиоценивается отношением
отчетного уровня к
базисному, которое всегда представляет собой
положительное число.
Показатель
интенсивности
изменения
уровня ряда в зависимости от того, выражается ли
он в виде коэффициента или в процентах, принято
называть коэффициентом роста.
Коэффициент
роста
и
темп
роста
представляют собой две формы выражения
интенсивности изменения уровня, отличающиеся
единицами измерения.
19
20.
Коэффициент роста показывает, во сколькораз данный уровень ряда больше базисного уровня
(если этот коэффициент больше единицы) или
какую часть базисного уровня составляет уровень
текущего периода за некоторый промежуток
времени (если он меньше единицы).
Темп роста вычисляется в процентах,
рассчитывается двумя способами.
Т рц
yi
100%
yi 1
Т рб
yi
100%
y0
цепным
базисным
20
21.
Темп прироста показывает, на какуюдолю (или процент) уровень данного периода
или момента времени больше (или меньше)
базисного уровня.
Темп
прироста
определяется
как
отношение абсолютного прироста к уровню ряда,
принятого за базу сравнения или как разность
между соответствующими темпами роста и 100
%:
Т прц Т рц 100 %
Т прб Т рб 100%
цепной
базисный
21
22.
Абсолютноезначения
одного
процента прироста (снижения) представляет
собой одну сотую часть базисного уровня или
определяется
как
отношение
абсолютного
прироста к соответствующему темпу прироста:
Абсолютное
значение
1
%
прироста
(снижения):
yi 1
А1%
100
22
23. Расчет аналитических показателей ряда динамики
РАСЧЕТ АНАЛИТИЧЕСКИХ ПОКАЗАТЕЛЕЙ РЯДА ДИНАМИКИПоказатель
Базисный
Цепной
1. Абсолютный прирост Δ
2. Коэффициент роста Кр
3. Темп роста Тр
4. Темпе прироста Тпр
5. Абсолютное значение 1%
прироста (А)
yi 1
;
100
23
24.
4. К средним показателям в рядах динамикиотносятся:
- средний уровень ряда;
- средний абсолютный прирост;
- средний темп роста;
- средний темп прироста.
Методы
расчета
среднего
уровня
интервального и моментного рядов динамики
различны.
Для
интервальных
рядов
с
равностоящими
уровнями
средний
уровень
находится по формуле средней арифметической
простой, а для неравноотстоящих
уровней средней арифметической взвешенной.
24
25.
Среднийуровень
моментного
равноотстоящего ряда динамики находится по
формуле средней хронологической простой.
Обобщающим
показателем
скорости
изменения явления во времени является средний
абсолютный прирост.
Этот
показатель
дает
возможность
установить, насколько в среднем за единицу
времени
должен
увеличиваться
(снижаться)
уровень ряда в абсолютном выражении, чтобы,
отправляясь от начального уровня за данное число
периодов (например, лет), достичь конечного
уровня.
25
26.
Для его вычисления применяется формула:y n y1
y
n 1
Средний темп роста показывает, во
сколько раз в среднем за единицу времени
изменяется
уровень
динамического
ряда.
Определяется по средней геометрической из
цепных коэффициентов роста:
Tp
n 1
K1 K 2... K
n 1
ПКi.
26
27.
Средний темп роста может быть выраженформулой:
Tp
n 1
yn
100%
y1
Средний темп прироста:
T пр Т
р
100%
27
28.
Средние показателиy
1. Уровень ряда
1 х х х 1 х
1
2
n 1
n
2
2
Х
n 1
y
y
Tр
n 1
yб
n 1
y
2. Абсолютный прирост
4. Темп прироста
n
___
3. Темп роста
y
y
ц
n 1
y n y1
n 1
T рбп
T р n 1 T p1 * T p2 * ... * T pn
Tпр T p 1
Tпр T p 100%
28
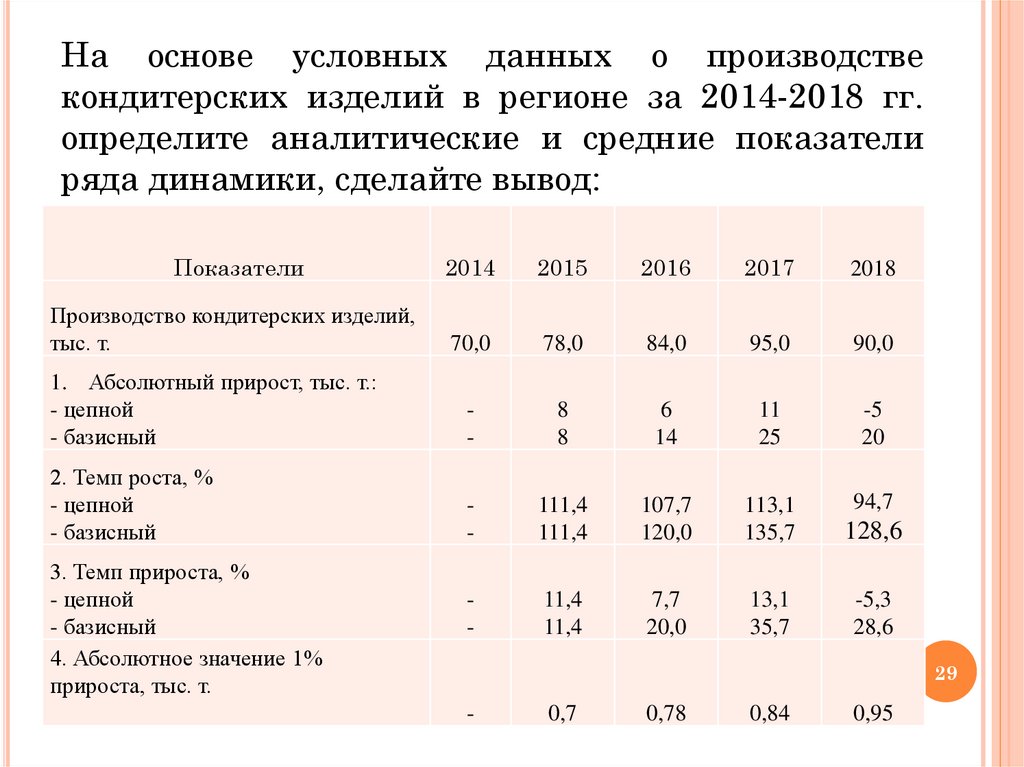
29.
На основе условных данных о производствекондитерских изделий в регионе за 2014-2018 гг.
определите аналитические и средние показатели
ряда динамики, сделайте вывод:
Показатели
2014
2015
2016
2017
2018
Производство кондитерских изделий,
тыс. т.
70,0
78,0
84,0
95,0
90,0
1. Абсолютный прирост, тыс. т.:
- цепной
- базисный
-
8
8
6
14
11
25
-5
20
2. Темп роста, %
- цепной
- базисный
-
111,4
111,4
107,7
120,0
113,1
135,7
94,7
128,6
-
11,4
11,4
7,7
20,0
13,1
35,7
-5,3
28,6
3. Темп прироста, %
- цепной
- базисный
4. Абсолютное значение 1%
прироста, тыс. т.
29
-
0,7
0,78
0,84
0,95
30.
Определяем средние показатели:1. Средний уровень ряда:
y 70 78 84 95 90
y
83,4тыс.т
n
5
2. Определим средний абсолютный прирост:
y
y
n 1
8 6 11 5
5 тыс. т.
4
3. Средний темп роста:
Т
р
n 1
yn
y1
4
90
70
4
1,28 *100% 106,5%
4. Средний темп прироста:
T пр Т р 100% 106,5% 100% 6,5%
30
31.
5. Важным направлением в исследованиизакономерностей
динамики
социальноэкономических процессов является изучение
общей тенденции развития (тренда).
Выделение тренда может быть произведено тремя
методами:
1. Укрупнения интервалов.
2. Скользящей средней.
3. Аналитического выравнивания.
Для наглядного представления тренда
применяется метод укрупнения интервалов, основанный на укрупнении периодов времени, к
которым относятся уровни ряда. Например
имеются уровни ряда динамики за 12 месяцев,
можно укрупнить по кварталам.
31
32.
Применяется формула средней арифметическойпростой.
Скользящая средняя – это подвижная
динамическая средняя, которая исчисляется по
ряду при последовательном передвижении на
один интервал, т.е. сначала вычисляют средний
уровень из определенного числа первых по
порядку уровней ряда, затем – средний уровень из
того же числа членов, начиная со второго уровня,
далее - начиная с третьего и т. д.
Таким
образом, при расчетах среднего
уровня как бы «скользят» по ряду динамики от его
начала к концу, каждый раз отбрасывая один
уровень в начале и добавляя один следующий.
Отсюда название - скользящая средняя.
32
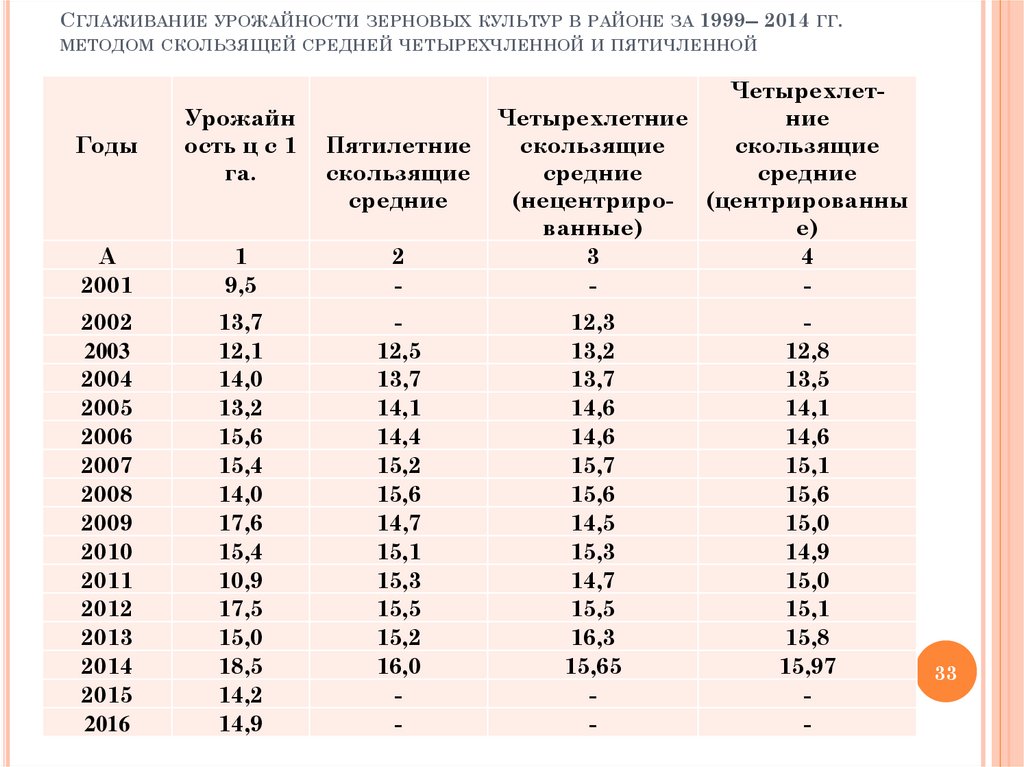
33. Сглаживание урожайности зерновых культур в районе за 1999-- 2014 гг. методом скользящей средней четырехчленной и пятичленной
СГЛАЖИВАНИЕУРОЖАЙНОСТИ ЗЕРНОВЫХ КУЛЬТУР В РАЙОНЕ ЗА
1999-- 2014 ГГ.
МЕТОДОМ СКОЛЬЗЯЩЕЙ СРЕДНЕЙ ЧЕТЫРЕХЧЛЕННОЙ И ПЯТИЧЛЕННОЙ
Годы
Урожайн
ость ц с 1
га.
А
2001
1
9,5
2
-
2002
2003
2004
2005
2006
2007
2008
2009
2010
2011
2012
2013
2014
2015
2016
13,7
12,1
14,0
13,2
15,6
15,4
14,0
17,6
15,4
10,9
17,5
15,0
18,5
14,2
14,9
12,5
13,7
14,1
14,4
15,2
15,6
14,7
15,1
15,3
15,5
15,2
16,0
-
Пятилетние
скользящие
средние
ЧетырехлетЧетырехлетние
ние
скользящие
скользящие
средние
средние
(нецентриро- (центрированны
ванные)
е)
3
4
12,3
13,2
13,7
14,6
14,6
15,7
15,6
14,5
15,3
14,7
15,5
16,3
15,65
-
12,8
13,5
14,1
14,6
15,1
15,6
15,0
14,9
15,0
15,1
15,8
15,97
-
33
34.
Применение в анализе рядов динамикиметодов укрупнения интервалов и скользящей
средней позволяет выявить тренд для описания
ряда, но получить обобщенную оценку тренда
можно
достичь
методом
аналитического
выравнивания.
Основным содержанием которого является
то, что основная тенденция ряда динамики
рассчитывается как функция времени:
34
35.
В разных случаях можно применятьуравнение прямолинейной функции, параболы,
гиперболы и других функций (полиномы разной
степени).
Простейшим
способом
аналитического
выравнивания является выравнивание по прямой
(полином первой степени), которое имеет вид:
y t a 0 a1t
35
36.
полином второй степени:y t a 0 a1t a 2 t
2
полином третьей степени:
y t a 0 a1t a 2 t a 3 t
2
3
36
37.
полином n-й степени:yt a0 a1t a2t ... ant
2
n
37
38.
Рассмотрим расчет параметров уравнения попрямой. Решить это уравнение значит найти
параметры a
и
a.
0
1
Достигается это при помощи метода
наименьших квадратов. Найти параметры
уравнения можно решив систему, состоящую из
двух уравнений:
na0 a1 t y;
a0 t a1 t 2 yt;
38
39.
Метод наименьших квадратов заключаетсяв том, что показателям времени придаем такие
значения, чтобы их сумма была равна 0 (если n –
нечетное число, то обозначения времени имеют 0 в
середине ряда динамики).
В этом случае система, состоящая из двух
уравнений принимает вид:
a0 n y;
a1 t yt;
2
39
40.
у- уровни фактического ряда динамики;n- число уровней ряда динамики.
Рассмотрим
метод
аналитического
выравнивания по прямой на примере:
Имеются данные о потреблении овощей на
одного члена домохозяйства за месяц за 20032017 гг. Определите основную тенденцию
потребления
овощей
на
одного
члена
домохозяйства
методом
аналитического
выравнивания по прямой.
40
41.
ГодПотребление
t
t2
yt
Yt
овощей, кг
2003
13,7
-7
49
-95,9
13,6
2004
12,1
-6
36
-72,6
13,8
2005
14,0
-5
25
-70,0
13,9
2006
13,2
-4
16
-52,8
14,1
2007
15,6
-3
9
-46,8
14,3
2008
15,4
-2
4
-30,8
14,5
2009
14,0
-1
1
-14,0
14,6
2010
17,6
0
0
0
14,8
2011
15,4
1
1
15,4
15,0
2012
10,9
2
4
21,8
15,1
2013
17,5
3
9
52,5
15,3
2014
15,0
4
16
60,0
15,5
2015
18,5
5
25
92,5
15,7
2016
14,2
6
36
85,2
15,8
41
42.
6. Сезонными называются колебания, которыеимеют определенный
и постоянный цикл,
равный годовому промежутку времени.
Ряд динамики при этом называют
сезонным рядом динамики.
Сезонные колебания наблюдаются в
различных видах экономической деятельности:
при
производстве
различных
сельскохозяйственных
продуктов,
при
реализации верхней одежды, обуви и т.д.
Сезонные колебания обычно отрицательно
влияют
на
результаты
производственной
деятельности, поэтому статистика занимается
изучением сезонных колебаний.
42
43.
Существует несколько методов изучениясезонных колебаний, из которых наиболее
простым является расчет индексов сезонности,
совокупность которых образует сезонную волну.
Для
расчета
индексов
сезонности
необходимо иметь помесячные данные, минимум
за три года.
Для каждого месяца за три года
рассчитывается
средний
уровень,
затем
исчисляется среднемесячный уровень для всего
анализируемого ряда.
По этим данным определяется индекс
сезонности:
Is
yi
100%
y
43
44.
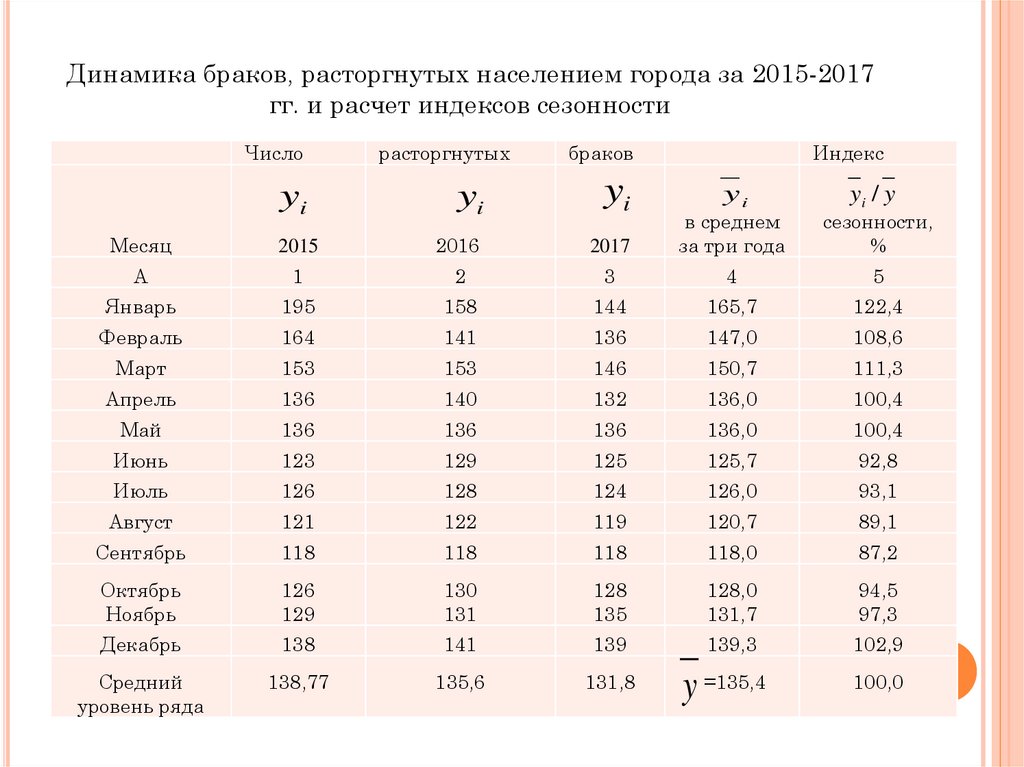
Динамика браков, расторгнутых населением города за 2015-2017гг. и расчет индексов сезонности
Число
yi
расторгнутых
браков
yi
yi
Индекс
yi
yi / y
Месяц
2015
2016
2017
в среднем
за три года
А
1
2
3
4
5
Январь
195
158
144
165,7
122,4
Февраль
164
141
136
147,0
108,6
Март
153
153
146
150,7
111,3
Апрель
136
140
132
136,0
100,4
Май
136
136
136
136,0
100,4
Июнь
123
129
125
125,7
92,8
Июль
126
128
124
126,0
93,1
Август
121
122
119
120,7
89,1
Сентябрь
118
118
118
118,0
87,2
Октябрь
Ноябрь
126
129
130
131
128
135
128,0
131,7
94,5
97,3
Декабрь
138
141
139
139,3
102,9
Средний
уровень ряда
138,77
135,6
131,8
y =135,4
сезонности,
%
100,0
44
45.
7. Необходимым условием рыночных отношенийявляется составление надежных прогнозов
развития социально-экономических явлений и
процессов.
Прогнозы развития – это определение
будущих размеров экономических явлений.
Применение
прогнозирования
предполагает,
что
имеющаяся
тенденция
развития
сохраняется
в
прошлом
и
распространяется на будущее, т.е. прогноз
основан на экстраполяции.
Экстраполяцией
называется
нахождение
уровней
за
пределами
динамического ряда.
Экстраполяция проводимая в будущее
называется перспективной, а экстраполяция
45
46.
В зависимости от исходных данных ипринципов построения применяются три метода
экстраполяции:
1) Метод средних абсолютных приростов.
Применяется тогда, когда абсолютные приросты,
рассчитанные по годам более или менее
постоянны, т.е. динамический ряд развивается
по прямой. В этом случае формула для прогноза
имеет вид:
yi t yi y t,
46
47.
2.При
экстраполяции
уровня развития
изучаемого явления на базе ряда динамики со
стабильными темпами роста применяется метод
средних темпов роста:
yi t yi Т
t
p
3. Метод аналитического выравнивания.
Прогнозируемое значение может не
совпадать с фактическим значением, так как мы
не учитываем влияние множества случайных
факторов.
47
48.
Однако, если линиятренда определена
правильно, прогнозируемые показатели должны
совпадать
с
фактическими.
Помимо
прогнозируемого показателя определяют интервал,
в котором находится прогнозируемый показатель
по формуле:
1
yi t yi 2 1
n
48
49.
-2
(
y
y
)
i t
2
n k
49
50.
v100
%
___
y
50
51.
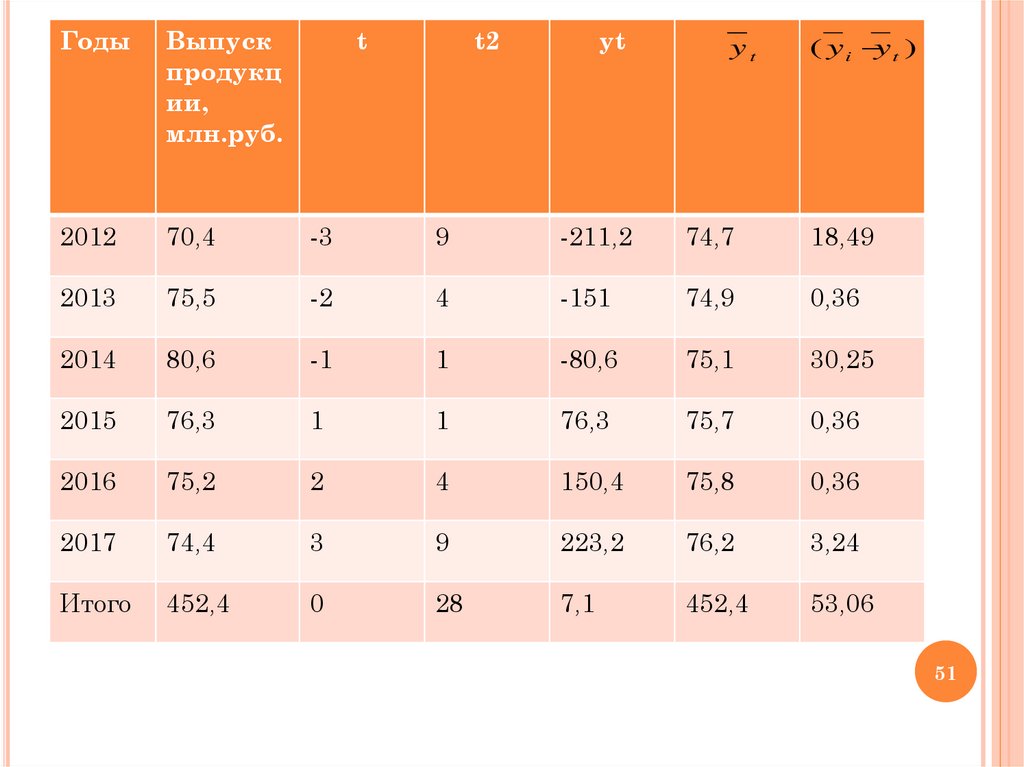
ГодыВыпуск
продукц
ии,
млн.руб.
t
t2
yt
2012
70,4
-3
9
-211,2
74,7
18,49
2013
75,5
-2
4
-151
74,9
0,36
2014
80,6
-1
1
-80,6
75,1
30,25
2015
76,3
1
1
76,3
75,7
0,36
2016
75,2
2
4
150,4
75,8
0,36
2017
74,4
3
9
223,2
76,2
3,24
Итого
452,4
0
28
7,1
452,4
53,06
yt
( y i y t )
51































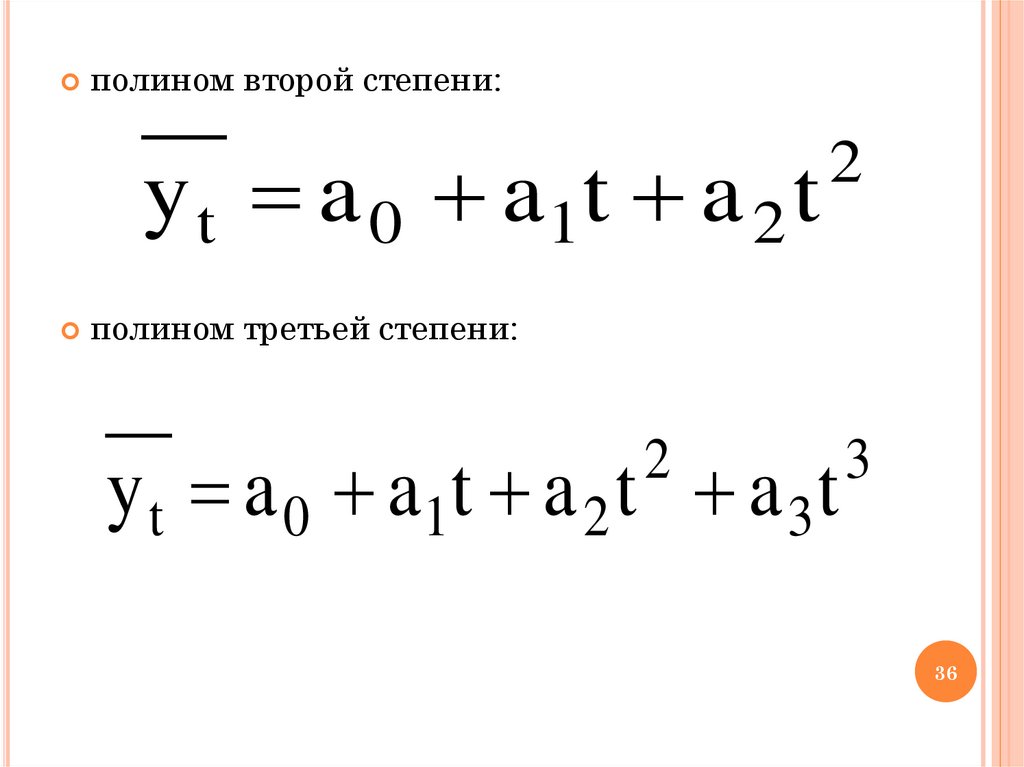
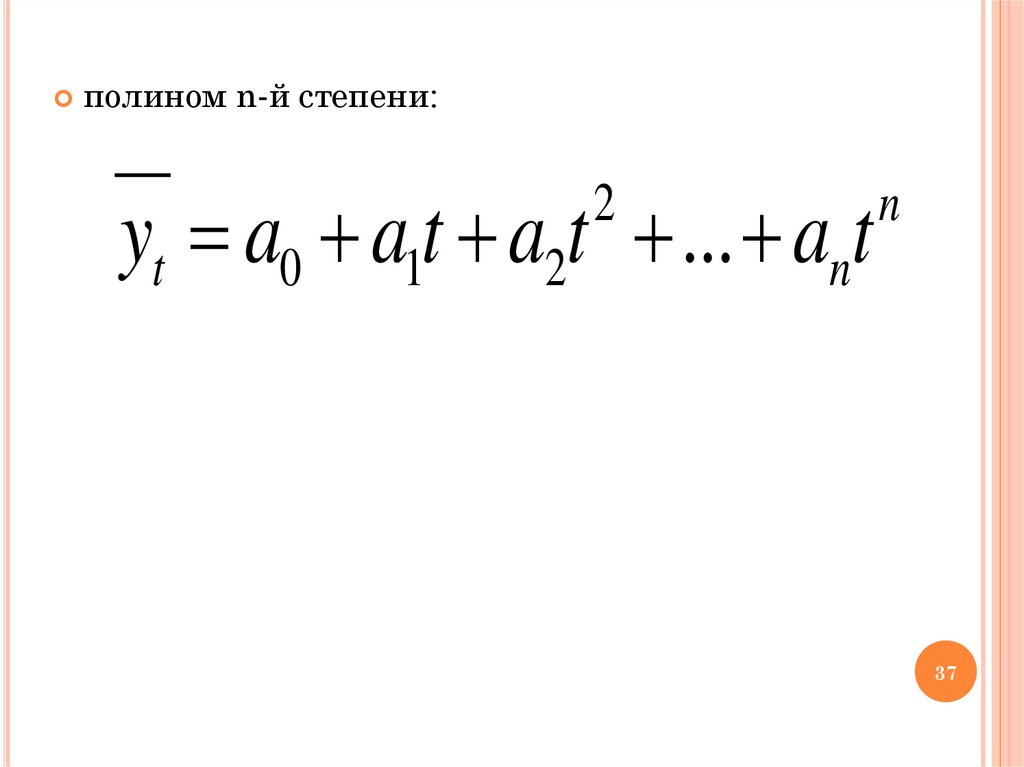










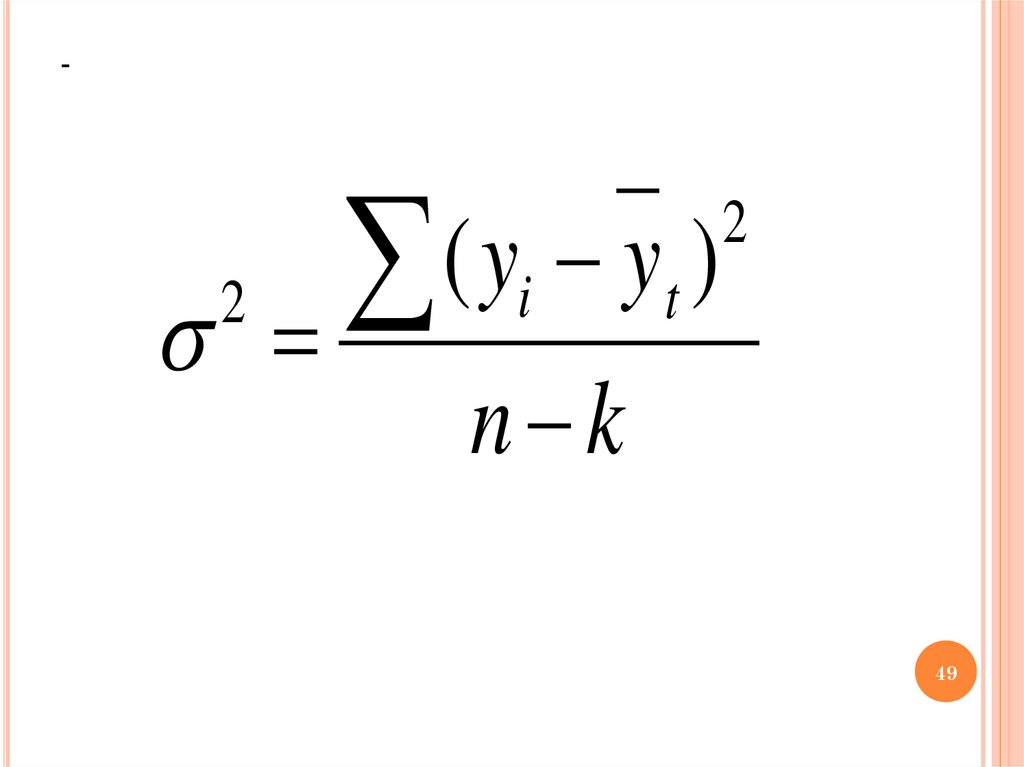
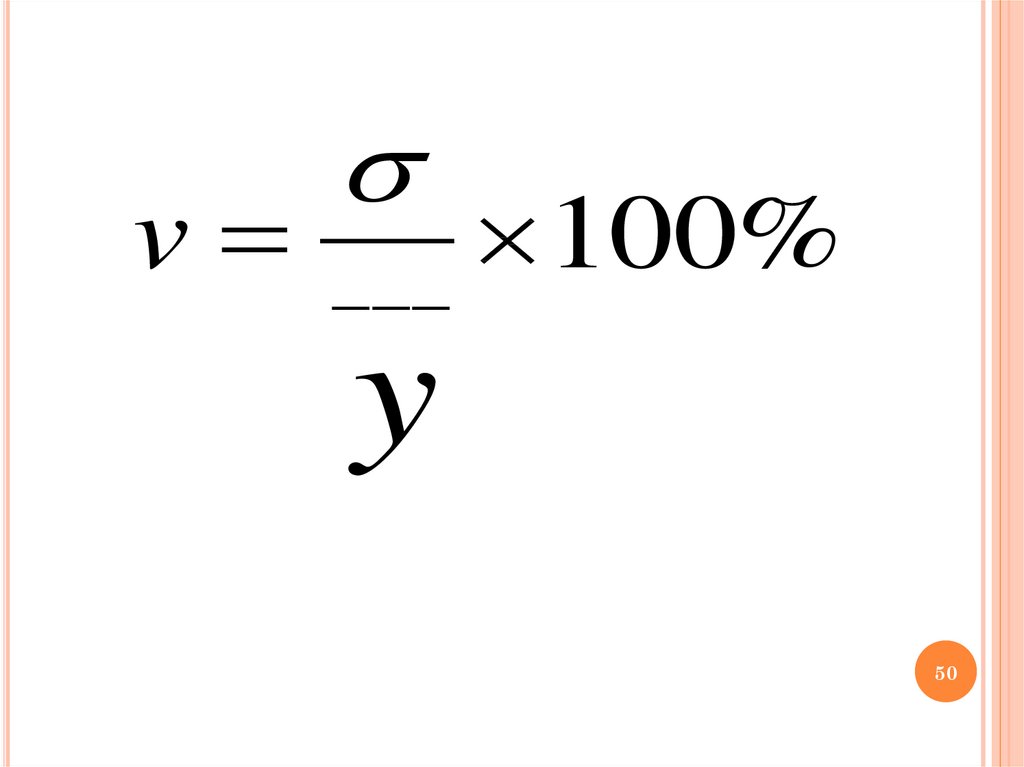
 mathematics
mathematics








