Similar presentations:
Ряды динамики. Элементы динамического ряда
1. Ряды динамики
2. Содержание
1. Понятие и виды рядов динамики2. Показатели анализа динамических рядов
3. Выявление основной тенденции развития в
рядах динамики
4. Экстраполяция в рядах динамики и
прогнозирование
5. Сезонные колебания в рядах динамики
3.
Ряд динамикипоследовательность
упорядоченных во времени
числовых показателей,
характеризующих уровень развития
изучаемого явления
(динамический ряд, временной ряд)
4.
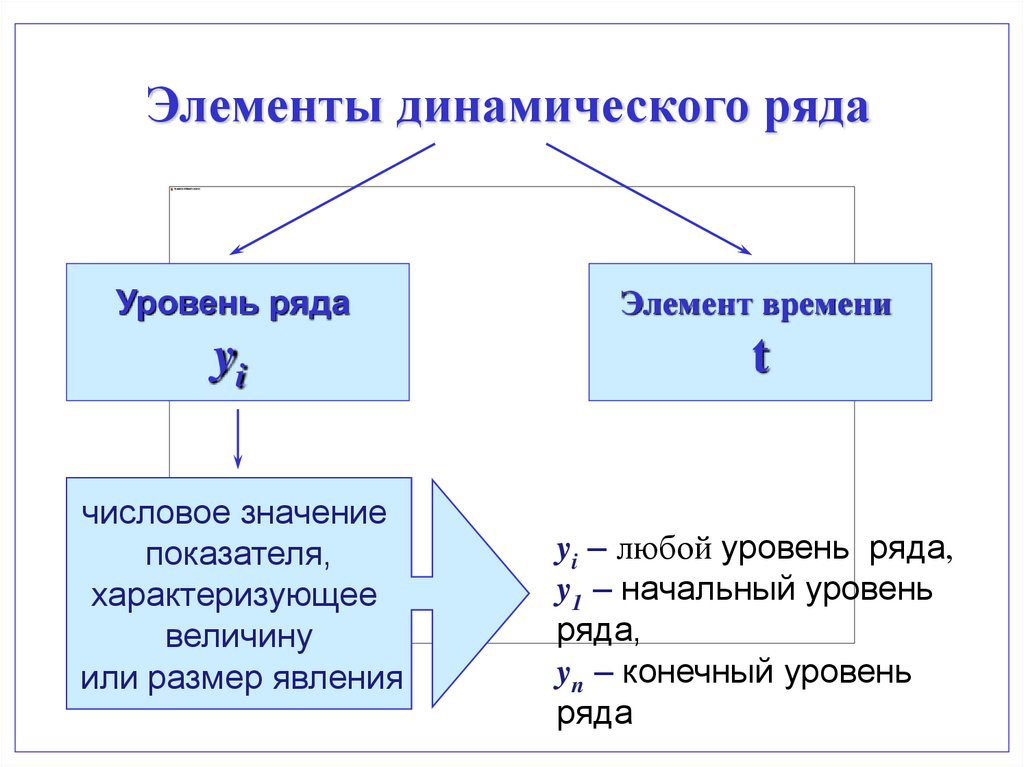
Элементы динамического рядаУровень ряда
Элемент времени
yi
t
числовое значение
показателя,
характеризующее
величину
или размер явления
yi – любой уровень ряда,
y1 – начальный уровень
ряда,
yn – конечный уровень
ряда
5.
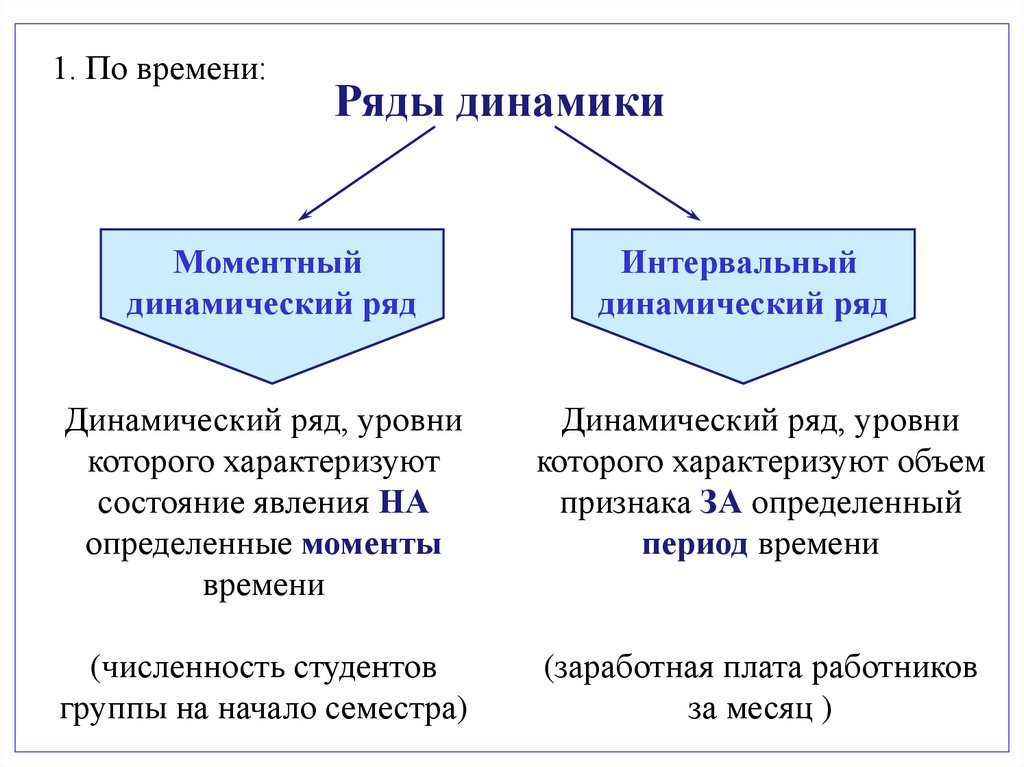
1. По времени:Ряды динамики
Моментный
динамический ряд
Интервальный
динамический ряд
Динамический ряд, уровни
которого характеризуют
состояние явления НА
определенные моменты
времени
Динамический ряд, уровни
которого характеризуют объем
признака ЗА определенный
период времени
(численность студентов
группы на начало семестра)
(заработная плата работников
за месяц )
6.
2. По форме представления • РД абсолютных величин (т/о);уровней:
• РД относительных величин
(индексы инфляции);
• РД средних величин
(потребление продуктов питания
на 1 члена семьи).
3. По длине интервала: - Равноотстоящие (полные);
- Неравноотстоящие (неполные)
4. По числу показателей: • Изолированные (одномерные);
• Многомерные (комплексные),
когда в хронологической
последовательности дается система
показателей, связанных между собой
единством процесса или явления.
7.
Основные правила построения рядов динамикиСтатистические данные должны быть:
1. достоверными, точными, научно обоснованными;
2. сопоставимы между собой по содержанию, т.е.
рассчитаны по одной и той же методике;
3. сопоставимы по территории, к которой относятся;
4. сопоставимы по времени, т.е. взяты за одинаковый
период или на одну и ту же дату;
5. сопоставимы по кругу охватываемых ими
объектов;
6. приведены в одинаковых единицах измерения.
8.
Причины несопоставимости данныхтерриториальные изменения (разные границы городов);
изменения единицы счета (пуды – тонны, масштаб цен);
различная степень охвата явления статистическими
наблюдениями (изменение количества товаров, входящих в
потребительскую корзину);
несовершенство методологии статистического наблюдения
(применение разной методологии при подсчете показателя).
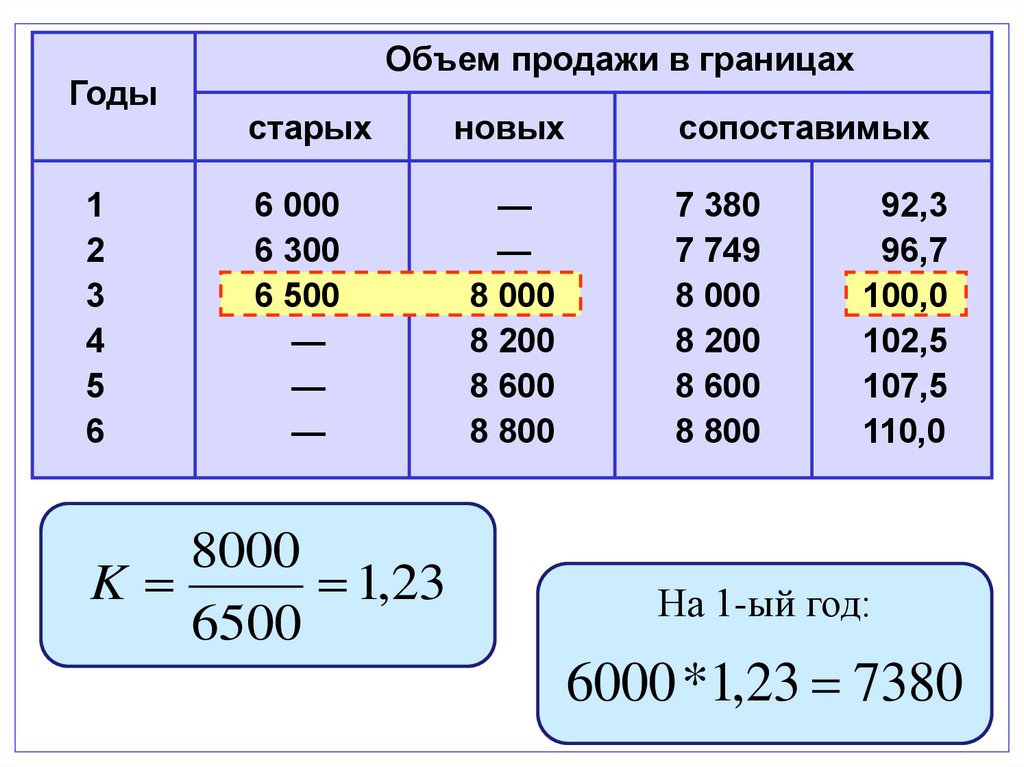
Для приведения уровней динамического ряда к
сопоставимому виду необходимо произвести смыкание
динамического ряда
9.
Годы1
2
3
4
5
6
Объем продажи в границах
старых
новых
сопоставимых
6 000
6 300
6 500
—
—
—
—
—
8 000
8 200
8 600
8 800
7 380
7 749
8 000
8 200
8 600
8 800
8000
K
1,23
6500
92,3
96,7
100,0
102,5
107,5
110,0
На 1-ый год:
6000 *1,23 7380
10.
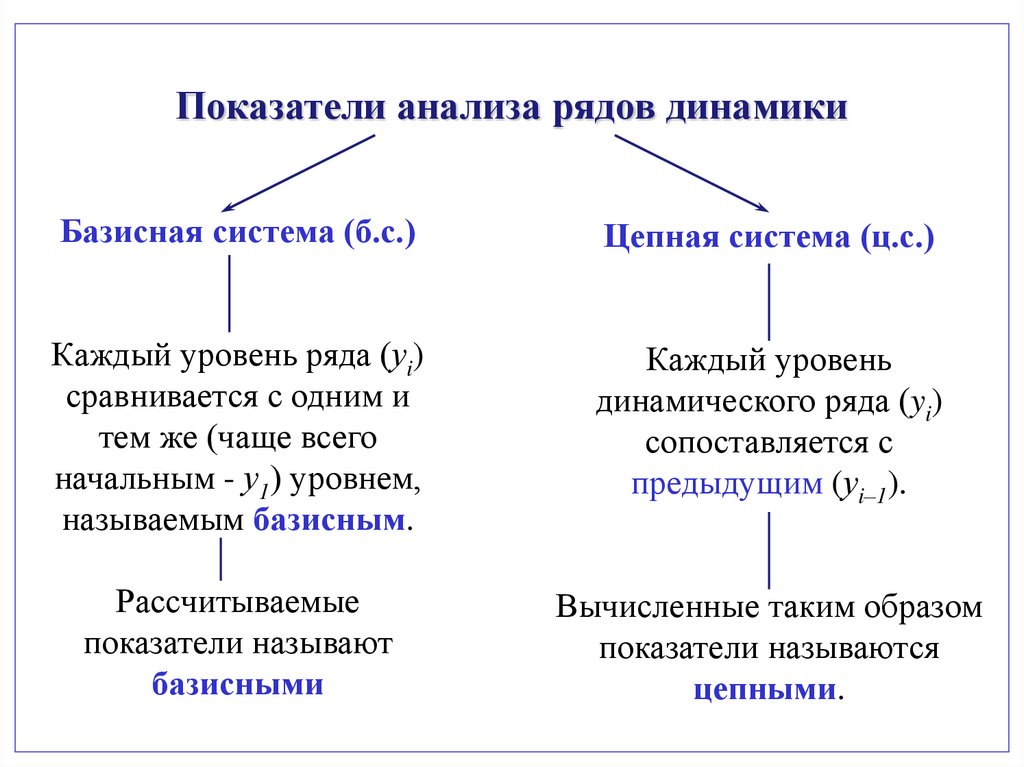
Показатели анализа рядов динамикиБазисная система (б.с.)
Цепная система (ц.с.)
Каждый уровень ряда (уi)
сравнивается с одним и
тем же (чаще всего
начальным - у1) уровнем,
называемым базисным.
Каждый уровень
динамического ряда (yi)
сопоставляется с
предыдущим (уi–1).
Рассчитываемые
показатели называют
базисными
Вычисленные таким образом
показатели называются
цепными.
11.
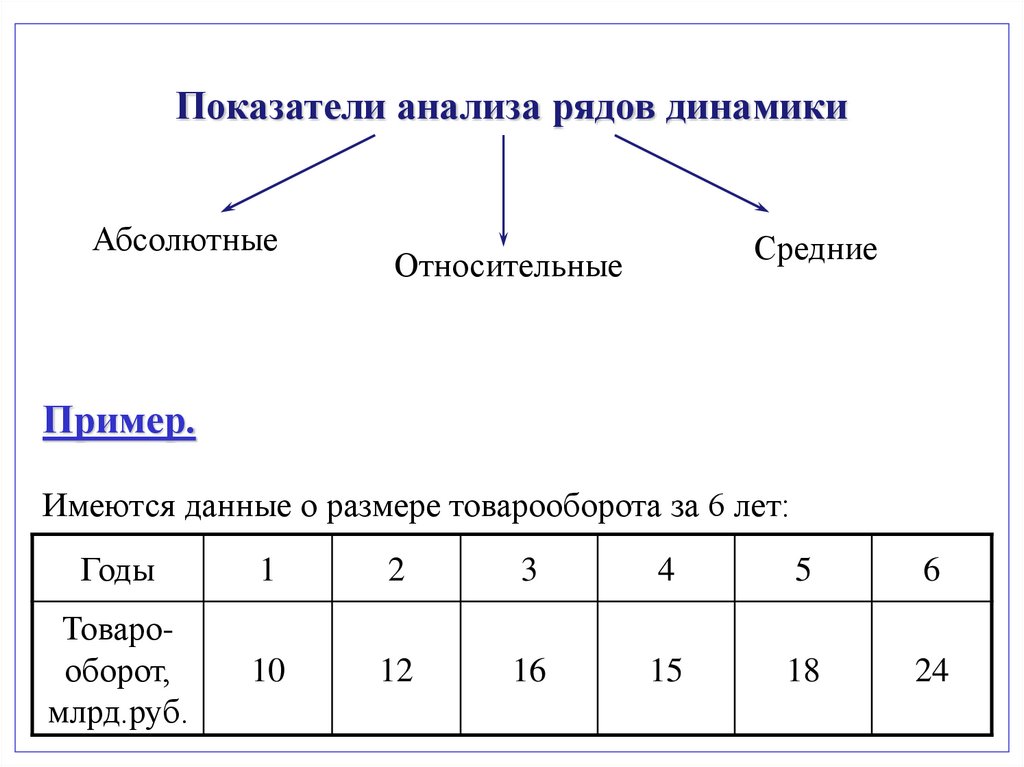
Показатели анализа рядов динамикиАбсолютные
Средние
Относительные
Пример.
Имеются данные о размере товарооборота за 6 лет:
Годы
1
2
3
4
5
6
Товарооборот,
млрд.руб.
10
12
16
15
18
24
12.
1. Абсолютные показатели анализа рядов динамикиАбсолютный прирост
Разность двух
уровней ряда
y(ц .с.) yi yi 1
12 - 10 = 2
16 - 12 = 4
y( б .с.) yi y1
12 - 10 = 2
16 - 10 = 6
13.
показывает, на сколько единиц увеличился(уменьшился) текущий уровень ряда по
сравнению с базисным или предыдущим уровнем;
может иметь положительный и отрицательный
знак;
измеряется в тех же единицах, что и уровни
ряда;
между базисными и цепными абсолютными
приростами имеется связь: сумма
последовательных цепных
y(абсолютных
ц.с.) y (бприростов
.с.)
n
равна базисному, т.е. общему приросту за весь
14.
2. Относительные показатели анализа рядов динамики2.1. Темп роста
Отношение текущего
уровня к предыдущему или
базисному
yi
Ty ( ц .с.)
100
yi 1
12
100 120 %
10
16
100 133 %
12
yi
Ty ( б .с.) 100
y1
12
100 120 %
10
16
100 160 %
10
15.
Показывает, во сколько раз увеличился (уменьшился)текущий уровень ряда по сравнению с базисным или
предыдущим:
> 1 (100%) - рост изучаемого уровня по сравнению с
базисным (предыдущим);
= 1 (100%) - текущий уровень по сравнению с базисным
(предыдущим) не изменился;
< 1 (100%) - уменьшение текущего уровня по
сравнению с базисным (предыдущим).
16.
показатель интенсивности изменения уровня ряда,выраженный в долях единицы, называется
коэффициентом роста, а в процентах – темпом
роста;
всегда имеет положительный знак;
между базисными и цепными темпами роста
существует взаимосвязь: произведение
последовательных цепных коэффициентов роста
равно базисному коэффициенту роста за весь период.
К р (ц.с.) К р (б.с.)
17.
2.2. Темп приростаTпр(ц .с.)
Tпр( б .с.)
у(ц .с.)
yi 1
у( б .с.)
y1
абсолютный прирост в
относительном выражении
2
4
100 % 20 %
100 % 33 %
100%
10
12
100%
2
6
100 % 20 %
100 % 60 %
10
10
18.
Исчисленный в процентах показывает, на сколькопроцентов изменился текущий уровень по
сравнению с базисным (предыдущим) уровнем
Между темпами прироста и темпами роста имеется
взаимосвязь:
Т Т 100%
пр
р
Поэтому если темп роста меньше 1 (100%), темп
прироста будет иметь отрицательный знак.
19.
2.3. Абсолютное содержание1% прироста
отношение
абсолютного прироста,
исчисленного по
цепной системе, к
цепному темпу
прироста (в %)
Показывает, сколько составляет в абсолютном
выражении каждый 1% прироста.
y i 1
y (ц.с.)
y (ц.с.)
1%
y i 1 0,01
Т пр (ц.с.) y (ц.с.)
100
100%
y i 1
20.
3. Средние показатели анализа рядов динамики3.1. Средний уровень
ряда динамики
характеризует типичную
величину уровня ряда
В интервальных рядах динамики с равными
периодами времени средний уровень определяется по
средней арифметической простой:
yt
_
y
n
В интервальных рядах динамики с неравными
периодами времени средний уровень определяется по
средней арифметической взвешенной:
yt , i t i
_
y
t
i
21.
Средний уровень моментного ряда сравноотстоящими моментами времени вычисляется
по формуле средней хронологической:
1
1
у1 у2 уn 1 уn
_
2
у 2
n 1
Если моментный ряд включает два значения, то
средний уровень рассчитывается по формуле:
yн yк
y1 y 2
y
y
или
2
2
y 10 12 16 15 18 24
y
n
6
95
15,8 млрд. руб
6
22.
3.2. Среднийабсолютный прирост
на сколько единиц в среднем
увеличивался (уменьшался)
изучаемый показатель на
протяжении
рассматриваемого периода
времени
y(б.с.) y n y 0
y
n 1
n 1
y (ц.с.)
y
n 1
24 10 14
y
2,8 млрд. руб
6 1
5
2 4 1 3 14
y
2,8 млрд. руб
6 1
5
23.
3.3. Средний темп ростаТ р n 1 Т р (ц.с.)
какими темпами в
среднем развивалось
изучаемое явление в
единицу времени
yn
Т р n 1 Т р (б.с.) n 1
y0
Tр 6 1 1,2 1,33 0,94 1,2 1,33 5 2,4 1,19
24
Tр 5
5 2,4 1,19
10
или 119 %
24.
3.4. Средний темпприроста
на сколько процентов в
среднем изменялось
изучаемое явление в
единицу времени
Т пр Т р 1 (100%)
119 % - 100 % = 19 %
25.
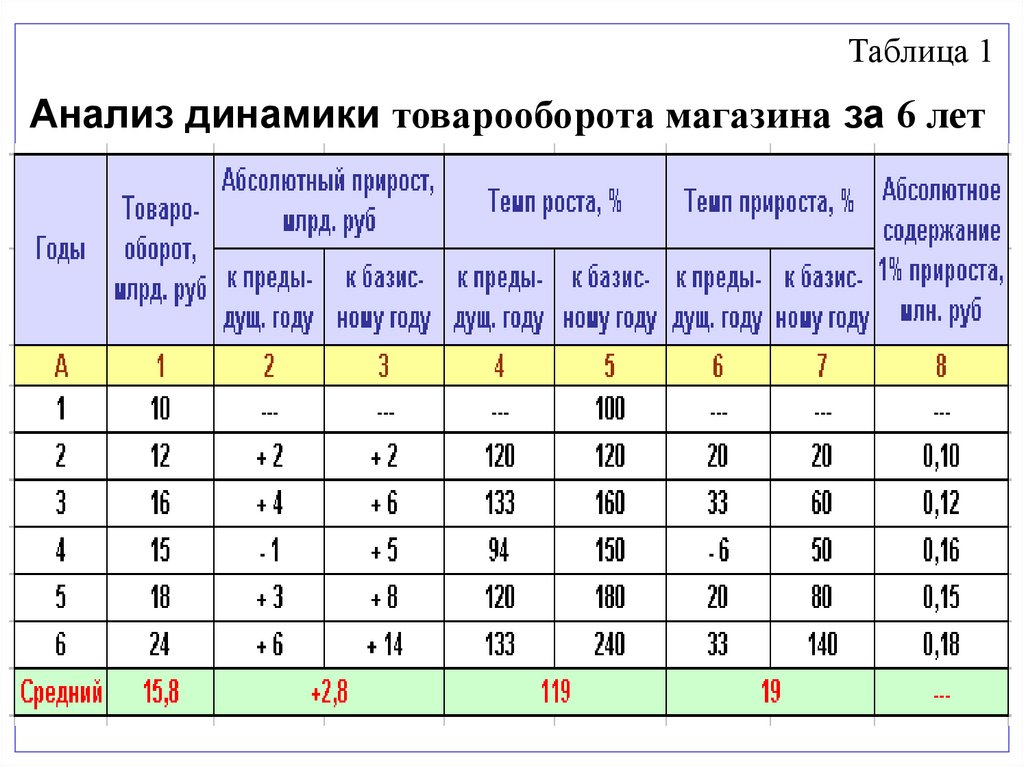
Таблица 1Анализ динамики товарооборота магазина за 6 лет
26.
Вывод:На протяжении исследуемого периода наблюдается
тенденция к увеличению товарооборота магазина. При
этом максимальный рост наблюдался в 6-м году: по
сравнению с 5-м годом товарооборот вырос на
6 млрд.руб. или 33%. В 4-м году наблюдалось
незначительное снижение размера товарооборота: по
сравнению с 3-м годом товарооборот магазина
уменьшился на 1 млрд.руб. или 6%. Средний размер
товарооборота магазина за 6 лет составил
15,8 млрд.руб. В среднем товарооборот ежегодно
увеличивался на 2,8 млрд.руб. или на 19 %. Всего же за
6 лет товарооборот магазина вырос на 14 млрд. руб.
или 140%.
27.
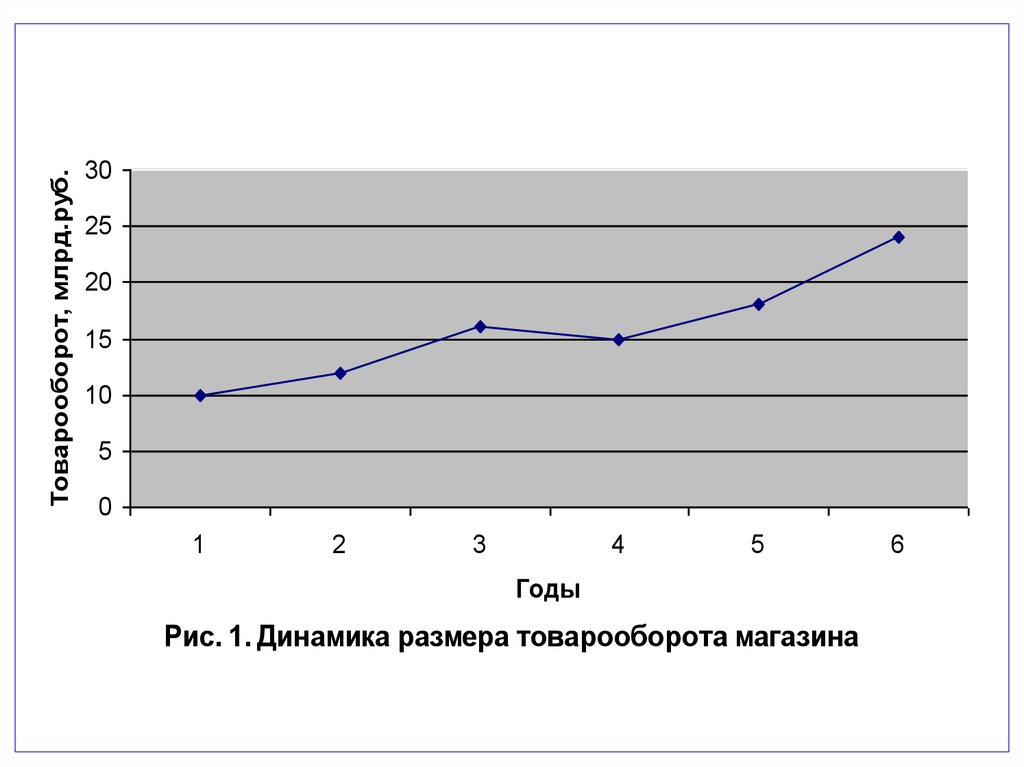
Товарооборот, млрд.руб.30
25
20
15
10
5
0
1
2
3
4
5
Годы
Рис. 1. Динамика размера товарооборота магазина
6
28.
Количественную оценку степени опереженияразвития одного явления по сравнению с другим дает
коэффициент опережения:
I
К опережения
Т р (б.с.)
II
Т р (б.с.)
Показывает, во сколько раз быстрее растут уровни
одного ряда по сравнению с другим.
При этом сравнении темпы должны характеризовать
тенденцию одного направления.
29.
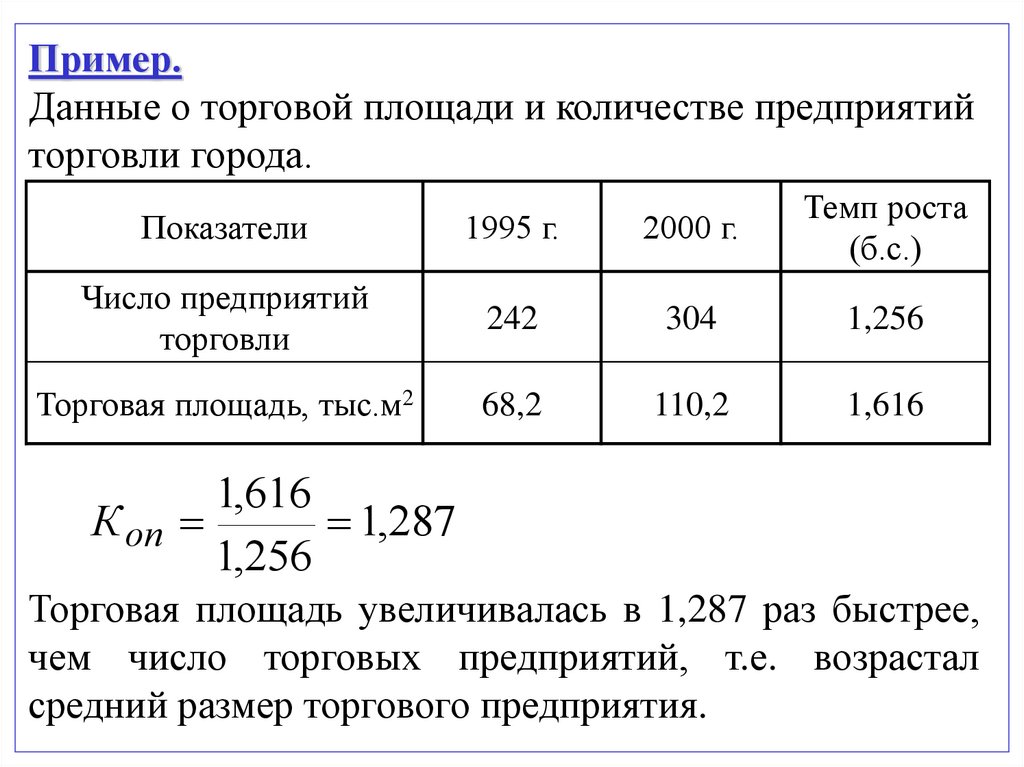
Пример.Данные о торговой площади и количестве предприятий
торговли города.
Показатели
1995 г.
2000 г.
Темп роста
(б.с.)
Число предприятий
торговли
242
304
1,256
Торговая площадь, тыс.м2
68,2
110,2
1,616
1,616
К оп
1,287
1,256
Торговая площадь увеличивалась в 1,287 раз быстрее,
чем число торговых предприятий, т.е. возрастал
средний размер торгового предприятия.
30.
Основная тенденция (ТРЕНД) плавное и устойчивое изменениеуровня явления во времени, свободное
от случайных колебаний
Формы представления: - графическая
- аналитическая
31.
1.Метод укрупнения интервалов и их
характеристика средними уровнями
переход от менее продолжительных интервалов к
более (сутки неделя декада месяц …), при
этом одновременно уменьшается количество
интервалов.
Если уровни ряда колеблются с определенной периодичностью,
то укрупненный интервал целесообразно взять равным периоду
колебаний.
Если такая периодичность отсутствует, то производится
постепенное укрупнение интервалов до тех пор, пока общее
направление тренда не станет отчетливым.
32.
У1 У 2 У 3У укр .1
3
У4 У5 У6
У укр .2
3
У7 У8 У9
У укр .3
3
33.
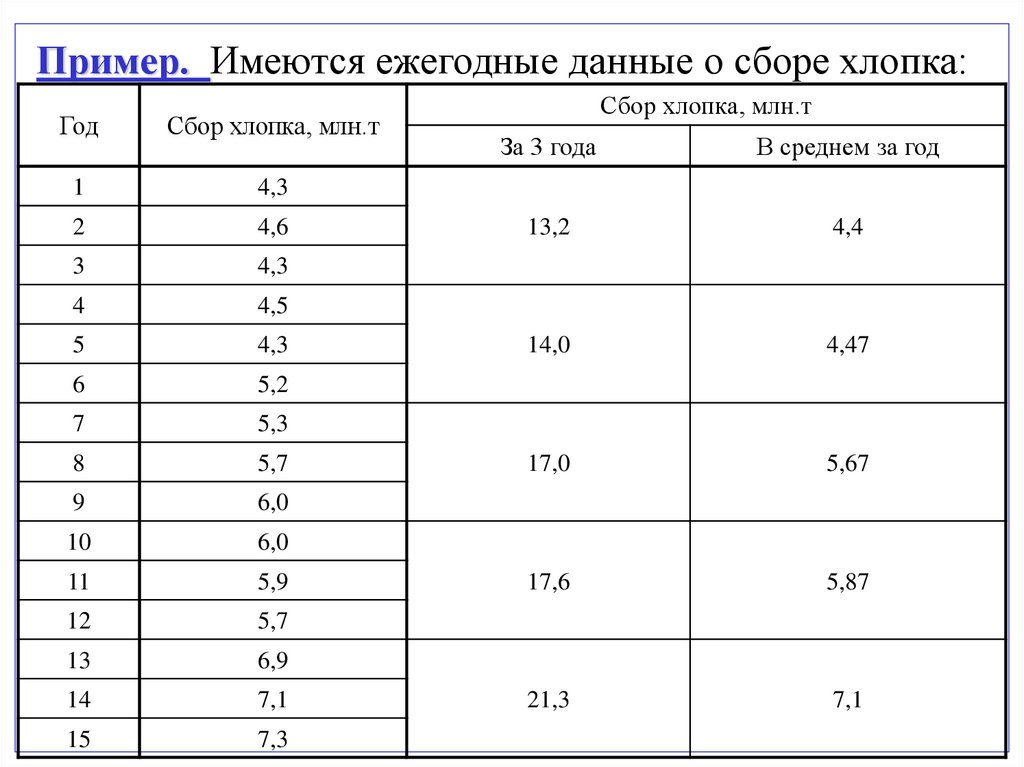
Пример. Имеются ежегодные данные о сборе хлопка:Год
Сбор хлопка, млн.т
1
4,3
2
4,6
3
4,3
4
4,5
5
4,3
6
5,2
7
5,3
8
5,7
9
6,0
10
6,0
11
5,9
12
5,7
13
6,9
14
7,1
15
7,3
Сбор хлопка, млн.т
За 3 года
В среднем за год
13,2
4,4
14,0
4,47
17,0
5,67
17,6
5,87
21,3
7,1
34.
2.Метод скользящей средней
замена фактических уровней рядом подвижных
(скользящих) средних, которые рассчитываются для
определенных последовательно подвижных интервалов
и относятся к середине каждого из них.
Для сглаживания, т.е. выявления тренда, необходимо
последовательно суммировать по k уровней и
результаты делить на k.
Т.е. исчисляется средний уровень из определенного числа,
обычно нечетного (3, 5, 7 и т.д.), первых по счету уровней, затем
– из такого же числа уровней, но начиная со 2-го по счету, далее
– начиная с 3-го и т.д.
35.
У1 У 2 У 3У ск .1
3
У2 У3 У4
У ск .2
3
У3 У4 У5
У ск .3
3
36.
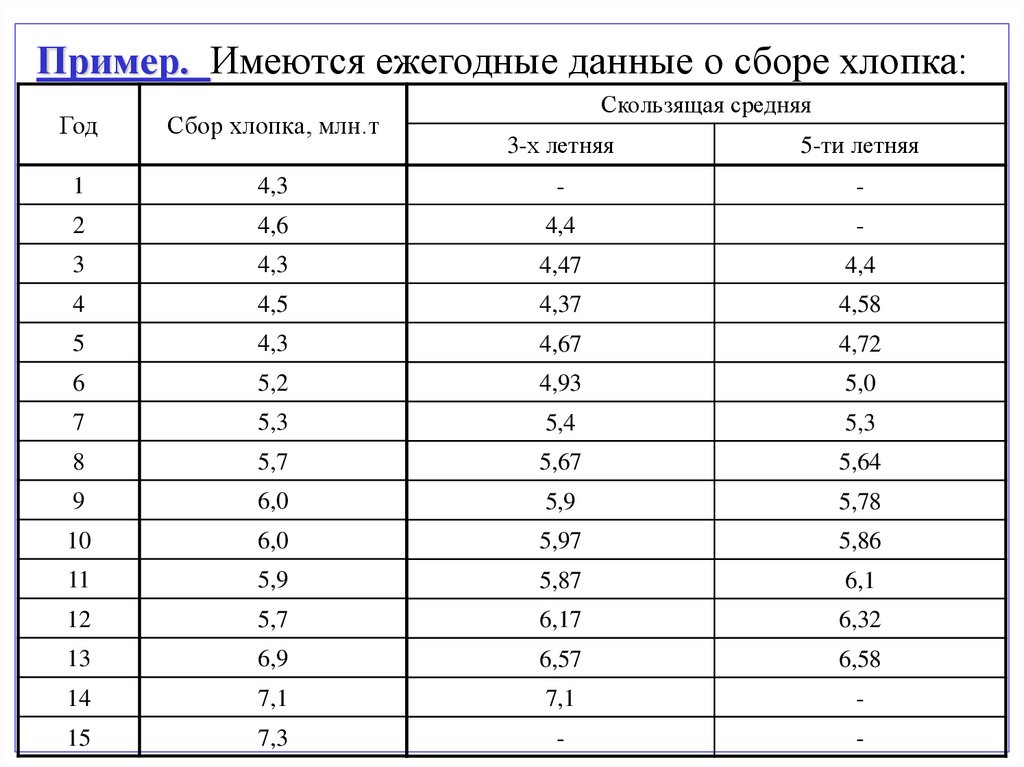
Пример. Имеются ежегодные данные о сборе хлопка:Год
Сбор хлопка, млн.т
1
Скользящая средняя
3-х летняя
5-ти летняя
4,3
-
-
2
4,6
4,4
-
3
4,3
4,47
4,4
4
4,5
4,37
4,58
5
4,3
4,67
4,72
6
5,2
4,93
5,0
7
5,3
5,4
5,3
8
5,7
5,67
5,64
9
6,0
5,9
5,78
10
6,0
5,97
5,86
11
5,9
5,87
6,1
12
5,7
6,17
6,32
13
6,9
6,57
6,58
14
7,1
7,1
-
15
7,3
-
-
37.
Сглаженный ряд сбора хлопка по 3-хлетиям корочефактического на один член ряда в начале и в конце, по
5-тилетиям – на два члена в начале и конце ряда.
Он меньше, чем фактический подвержен колебаниям
из-за случайных причин, и четче выражает основную
тенденцию роста сбора хлопка за изучаемый период,
связанную с действием долговременно существующих
причин и условий развития.
Недостаток сглаживания ряда:
«укорачивание» от начала и от конца на
k 1
2
уровней по сравнению с фактическим рядом, а
следовательно, потеря информации.
38.
3.Аналитическое выравнивание
уровни ряда динамики выражаются
в виде функции времени:
y t f (t )
yt
- уровни динамического ряда, вычисленные по
соответствующему аналитическому уравнению на
момент времени t.
Уравнение, которое выражает зависимость уровней
динамического ряда от фактора времени t , называется
уравнением тренда.
39.
Простейшие модели, выражающие тенденциюразвития:
линейная функция – прямая
показательная функция
y t a0 a1t
yt a a
t
0 1
степенная функция – кривая 2-го порядка (парабола)
y t a0 a1t a2t
где а0, а1, а2 – параметры уравнения, t – время.
2
40.
Выравнивание по прямойy t a0 a1t
na0 a1 t y
2
a0 t a1 t yt
n - число уровней ряда динамики,
t - условное обозначение фактора времени
порядковыми номерами,
у - фактические уровни ряда динамики.
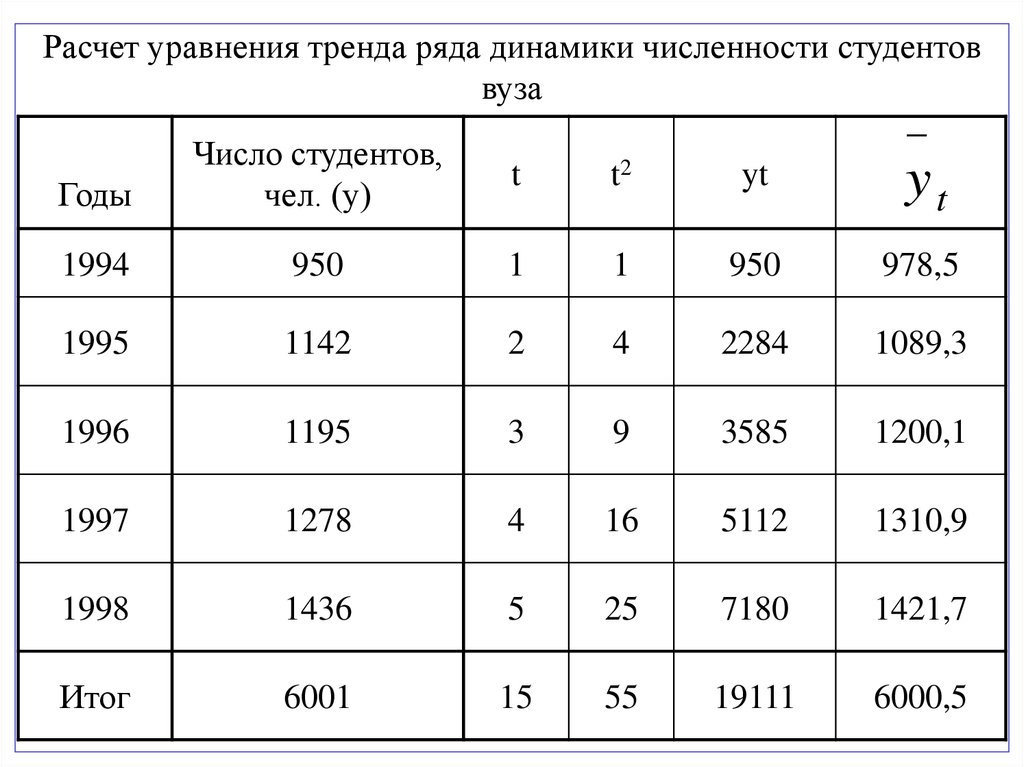
41.
Расчет уравнения тренда ряда динамики численности студентоввуза
Годы
Число студентов,
чел. (у)
t
t2
yt
yt
1994
950
1
1
950
978,5
1995
1142
2
4
2284
1089,3
1996
1195
3
9
3585
1200,1
1997
1278
4
16
5112
1310,9
1998
1436
5
25
7180
1421,7
Итог
6001
15
55
19111
6000,5
42.
5ао+ 15а1 = 60013
15ао+ 55а1 = 19111
15ао+ 45а1 = 18003
15а0 + 55а1 = 19111
10а1 = 1108
1108
а
110,8
1 10
4339
а
867,6
0
5
y t = 867,6 + 110,8t
43.
Для 1994 гДля 1995 г..
=y867,6
+ 110,8 1 = 978,5
t
=y 867,6 + 110,8 2 = 1089,3 и т.д.
t
Сумма фактических значений у и сумма выровненных должны
приближенно быть равны:
y
t у (6000,5 6001).
Если такого равенства нет, уравнение тренда рассчитано неверно.
Ряд выровненных значений характеризует тенденцию
стабильного возрастания числа студентов в вузе, при этом
численность студентов увеличивается в среднем на 110,8 чел. в
год.
44.
Экстраполяциянахождение уровней за пределами
изучаемого ряда, т.е. продление в
будущее тенденции, наблюдавшейся в
прошлом
45.
1.С помощью уравнения тренда
В уравнение тренда подставляют продолженное значение
времени.
Для 1999 г. t = 6
=y 867,6
+ 110,8 6 = 1532,5 (чел.)
6
Для 2000 г. t = 7
=y867,6
+ 110,8 7 = 1643,3 (чел.)
7
46.
2.С помощью среднего абсолютного прироста
y n k y n k y
где y - экстраполируемый уровень,
n k
k - период экстраполяций (год, два,....),
уn - последний уровень динамического ряда,
- средний абсолютный прирост.
y
1436 950 486
121,5
5 1
4
Прогноз численности студентов
на 1999 г.:
y6 y5 1 1436 1 121,5 1557,5 (чел.);
у
на 2000 г.:
y7 y5 2 1436 2 121,5 1679 (чел.).
47.
3.С помощью среднего темпа роста
к
yn k yn K p ,
где
K P - средний темп роста в коэффициентах
yn
1436 4
K P n 1
5 1
1,511 1,109 или 110,9 %.
y1
950
Прогноз
на 1999 г.:
на 2000 г.:
y6 y5 =1 1436 1,109 = 1592,5 (чел.);
2 = 1766,1 (чел.).
y 7 y 5 =1436 (1,109)
2
48.
Сезонные явлениявсе явления, которые обнаруживают в
своем развитии отчетливо выраженную
закономерность внутригодичных
изменений, т.е. более или менее устойчиво
повторяющиеся колебания уровней по
внутригодовым периодам: месяцам,
кварталам
49.
У iУi
n
У i
У
n
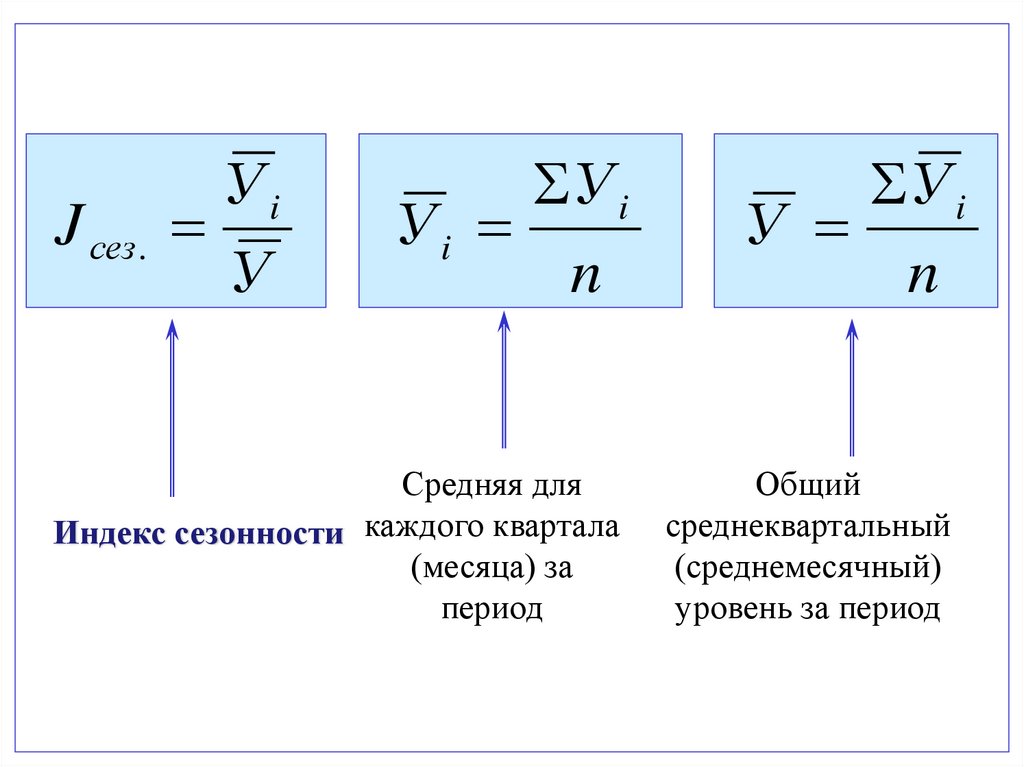
Средняя для
Индекс сезонности каждого квартала
(месяца) за
период
Общий
среднеквартальный
(среднемесячный)
уровень за период
Уi
J сез .
У
50.
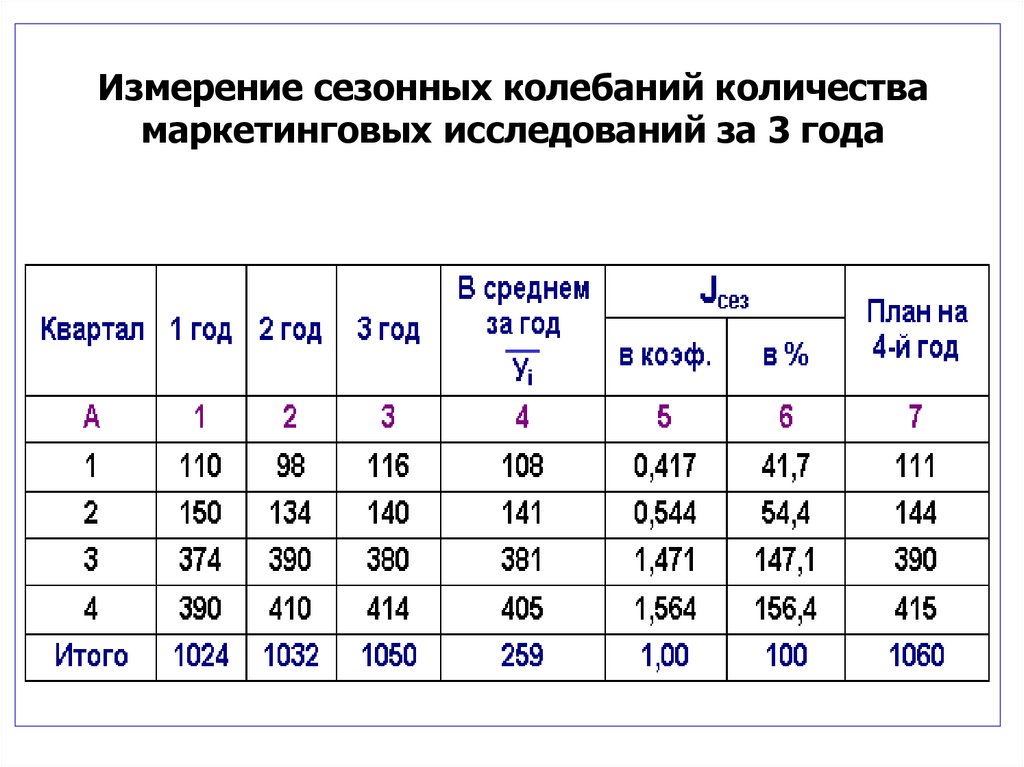
Измерение сезонных колебаний количествамаркетинговых исследований за 3 года
51.
110 98 116У1кв
108
3
108 141 381 405
У
259
4
1024 1032 1050
У
259
12 кварталов
108
J сез.1кв
0,417 или 41,7%
259
52.
Распределить 1060 маркетинговыхисследований на 4-й год по кварталам
У план i J сез . У план
1060
У план
265
4
У план 1кв. 265 0,417 111
У план 2 кв 265 0,544 144 и т.д.





































 mathematics
mathematics








