Similar presentations:
Комплéксные числа. Лекция 2
1. Здравствуйте!
Лекция №22. Комплéксные числа
3.
i 1i 1
2
4.
Алгебраическая форма комплексных чиселПусть х и у обычные вещественные числа. Число вида
z x iy
называется комплексным числом в алгебраической форме.
х называют действительной частью числа z, и обозначают так:
x Re(z ) . у называют мнимой частью числа z и обозначают так:
y Im(z ) . Если Im( z ) 0 , то число z называют действительным
числом; если Re( z ) 0 , то число z называют мнимым числом.
Число z x iy называется числом, комплексно сопряженным
числу z. Действует следующее общее правило: чтобы получить
число, комплексно сопряженное данному числу, надо в нем
заменить i на i.
5.
Рассмотрим операции над комплексными числами валгебраической форме. Пусть даны два комплексных числа
z1 x1 iy1 и z2 x2 iy2 .
Равенство и сравнение комплексных чисел
Два комплексных числа считаются равными, если у них равны
действительные части и мнимые части:
z1 z2 x1 x2 y1 y2 .
Но вот операции типа «больше» и «меньше» доя комплексных
чисел не имеют смысла, то есть бессмысленно писать z1 z2 или
z1 z2 . Совершенно непонятно, что больше: 2 3i или 3 2i .
Комплексные числа не упорядочены.
6.
Сложение и вычитание комплексных чиселСложение и вычитание двух комплексных чисел определяются
совершенно естественно
z1 z2 ( x1 iy1 ) ( x2 iy2 ) ( x1 x2 ) i( y1 y2 ) ,
то есть надо сложить (или вычесть) отдельно действительные и
мнимые части.
Умножение комплексных чисел
Умножение двух комплексных чисел также чисел также
определяется совершенно естественно. Надо лишь помнить, что
i 2 1:
z1 z2 ( x1 iy1 ) ( x2 iy2 ) x1 x2 ix1 y2 ix2 y1 i 2 y1 y2
( x1 x2 y1 y2 ) i( x1 y2 x2 y1 ) .
7.
Деление комплексных чиселДля деления комплексных чисел полезно запомнить следующее
правило: чтобы разделить два комплексных числа друг на друга
надо числитель и знаменатель умножить на число, комплексно
сопряженное знаменателю:
z1 x1 iy1 x1 iy1 x2 iy2
z2 x2 iy2 x2 iy2 x2 iy2
x1 x2 iy1 x2 ix1 y2 i 2 y1 y2 x1 x2 y1 y2
y1 x2 x1 y2
i
,
2
2 2
2
2
2
2
x2 i y2
x2 y2
x2 y2
где учтено, что i 2 1. Заметим, что при делении двух
комплексных чисел снова получается комплексное число.
8.
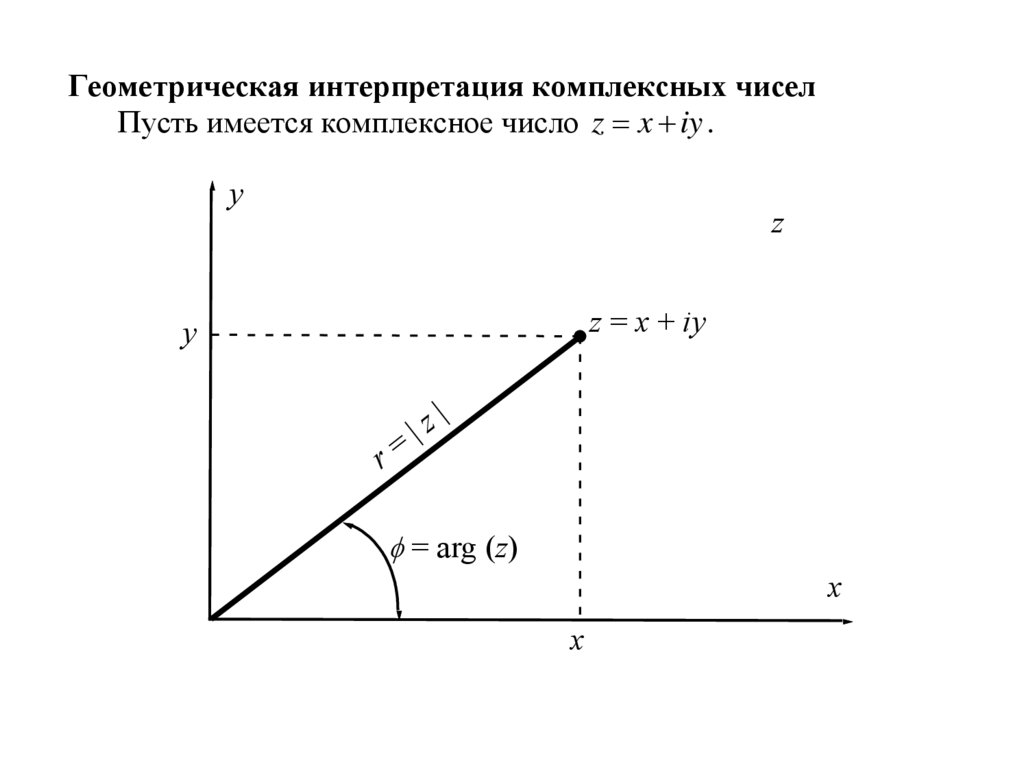
Геометрическая интерпретация комплексных чиселПусть имеется комплексное число z x iy .
y
z
z = x + iy
y
r
z
|
=
|
= arg (z)
x
x
9.
Тригонометрическая форма комплексных чиселС геометрической интерпретацией связана и еще одна форма
записи комплексных чисел, называемая тригонометрической
формой.
Соединим точку ( x, y ) с началом координат отрезком прямой.
Длина этого отрезка r называется модулем комплексного числа z и
обозначается как | z | или mod( z ) .
Угол , который этот отрезок образует с осью абсцисс,
называется аргументом комплексного числа z и обозначается как
arg( z ) . Он определяется с точностью до слагаемого 2 k .
Из рисунка видно, что имеет место соотношение x r cos ,
y r sin . Отсюда следует, что r x 2 y 2 z z , tg y x .
Таким образом, мы можем записать z x iy r cos ir sin , или
z r (cos i sin ) .
Эта форма записи и получила название комплексного числа в
тригонометрической форме.
10.
Рассмотрим операции над комплексными числами втригонометрической форме. Пусть имеется два комплексных числа
z1 r1 (cos 1 i sin 1 ) и z2 r2 (cos 2 i sin 2 ) .
Равенство чисел
Два
комплексных
числа
и
z1 r1 (cos 1 i sin 1 )
z2 r2 (cos 2 i sin 2 ) считаются равными, если r1 r2 и
1 2 2 k , k 0, 1, 2, 3, ...
11.
Умножение комплексных чиселИмеем
z1 z2 r1 (cos 1 i sin 1 ) r2 (cos 2 i sin 2 )
r1r2 (cos 1 cos 2 sin 1 sin 2 ) i(cos 1 sin 2 sin 1 cos 2 )
r1r2 cos( 1 2 ) i sin( 1 2 ) .
Таким образом, при перемножении комплексных чисел их
модули перемножаются, а аргументы складываются.
12.
Деление комплексных чиселИмеем
z1 r1 (cos 1 i sin 1 ) cos 2 i sin 2
z2 r2 (cos 2 i sin 2 ) cos 2 i sin 2
r1 (cos 1 cos 2 sin 1 sin 2 ) i (sin 1 cos 2 cos 1 sin 2 )
2
2
r2
cos 2 sin 2
r1
cos( 1 2 ) i sin( 1 2 ) .
r2
Таким образом, при делении комплексных чисел их модули
делятся, а аргументы вычитаются.
13.
Возведение в степеньПусть z r (cos i sin ) . Тогда, согласно сказанному выше,
n
zn
z
z z
z
r
(cos n i sin n ) ,
n раз
то есть при возведении в степень модуль возводится в эту степень,
а аргумент умножается на нее.
Отметим частный случай этой формулы. При r 1 получаем
(cos i sin )n cos n i sin n .
Эта формула называется формулой Муавра.
14.
Извлечение корнейПолученный выше результат позволяет вывести алгоритм
извлечения корней из комплексных чисел.
Пусть имеется комплексное число z r (cos i sin ) . Что
понимать под n z ?
Для ответа на этот вопрос вспомним прежде всего, что
аргумент комплексного числа определяется с точностью до 2 k то
есть
z r (cos( 2 k ) i sin( 2 k )) , k 0, 1, 2, 3, ...
15.
nz есть также комплексное число
Допустим, что
n
z z0 r0 (cos 0 i sin 0 ) . Но тогда должно иметь место
соотношение z z0n , или
r (cos( 2 k ) i sin( 2 k )) r0n (cos n 0 i sin n 0 ) .
Отсюда получаем, что r r0n , 2k n 0 , или
r0 n r ,
2k
0
. Таким образом
n
n
2k
2k
n
n
z r cos
i sin
.
n
n
n
n
Заметим, что разные значения n z получаются лишь для
k 0, n 1 , далее все повторяется. Таким образом, корень п-й
степени из комплексного числа имеет ровно п различных
значений.
16.
Формула Эйлера. Показательная форма комплексногочисла
Вспомним ряды Тейлора
2
3
4
5
6
x
x
x
x
x
x
e x 1 ...
,
1! 2! 3! 4! 5! 6!
x2 x4 x6
cos x 1 ... ,
2! 4! 6!
x x3 x5 x7
sin x ... .
1! 3! 5! 7!
Далее заметим, что i 1 ,
далее все повторяется.
2
i 3 i 2 i i , i 4 i 3 i 1
и
17.
Найдем теперь e ix . Имеем2
3
4
5
6
ix
(
ix
)
(
ix
)
(
ix
)
(
ix
)
(
ix
)
eix 1
...
1!
2!
3!
4!
5!
6!
x x3 x5 x7
x2 x4 x6
1 ... i ...
2! 4! 6!
1! 3! 5! 7!
cos x i sin x .
Мы получили знаменитую формулу Эйлера
e cos x i sin x .
ix
18.
Полезно помнить некоторые следствия из этой формулы.Заменяя в ней i на i, получим
e ix cos x i sin x .
Складывая и вычитая эти две формулы, получим
eix e ix
eix e ix
cos x
, sin x
.
2i
2
Вспоминая гиперболические функции, можем записать:
cos x ch( ix ) , sin x sh( ix) i ,
что говорит о родстве этих функций.
19.
Вернемся к комплексным числам. Имеемi
z r (cos i sin ) re
,
что и дает так называемую показательную форму комплексного
числа. Так как аргумент определяется с точностью до слагаемого
2k , то, в общем случае,
z re
i ( 2 k )
,
k 0, 1, 2, 3, ... .
20.
Эта формула позволяет определить логарифм комплексногочисла:
ln z ln r i ( 2k ) , k 0, 1, 2, 3, ... .
Заметим, что логарифм бесконечнозначная функция.
В частности, ln( 1) i ( 2k ) , k 0, 1, 2, 3, ..., так как
| 1 | 1 и arg( 1) .


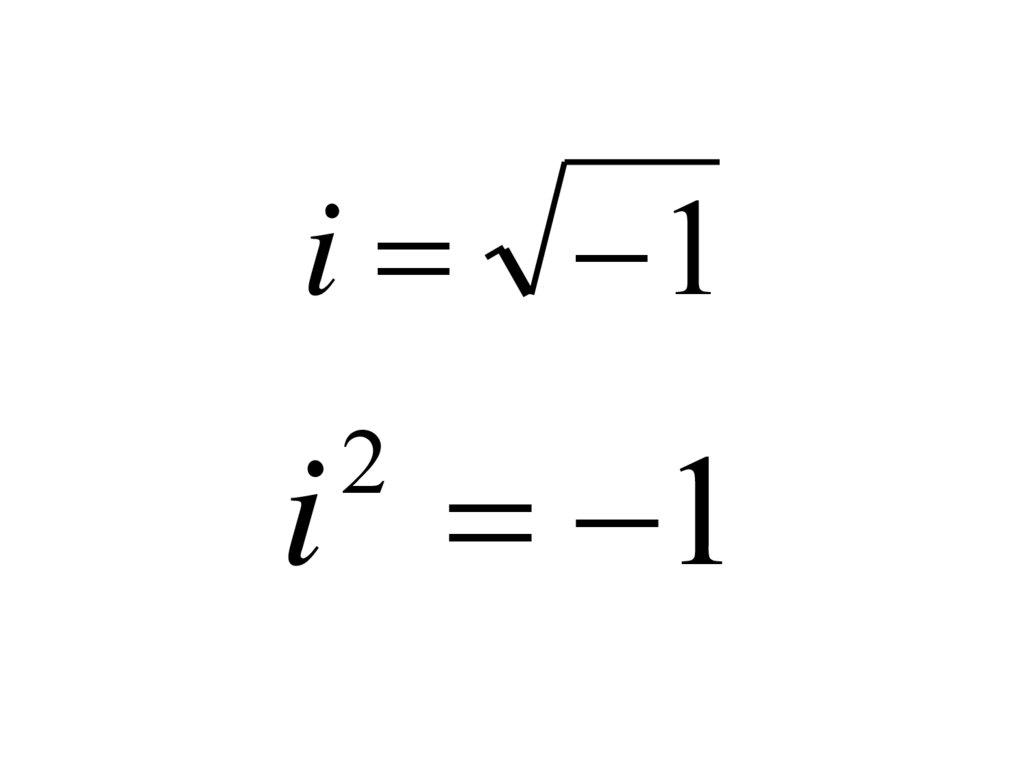












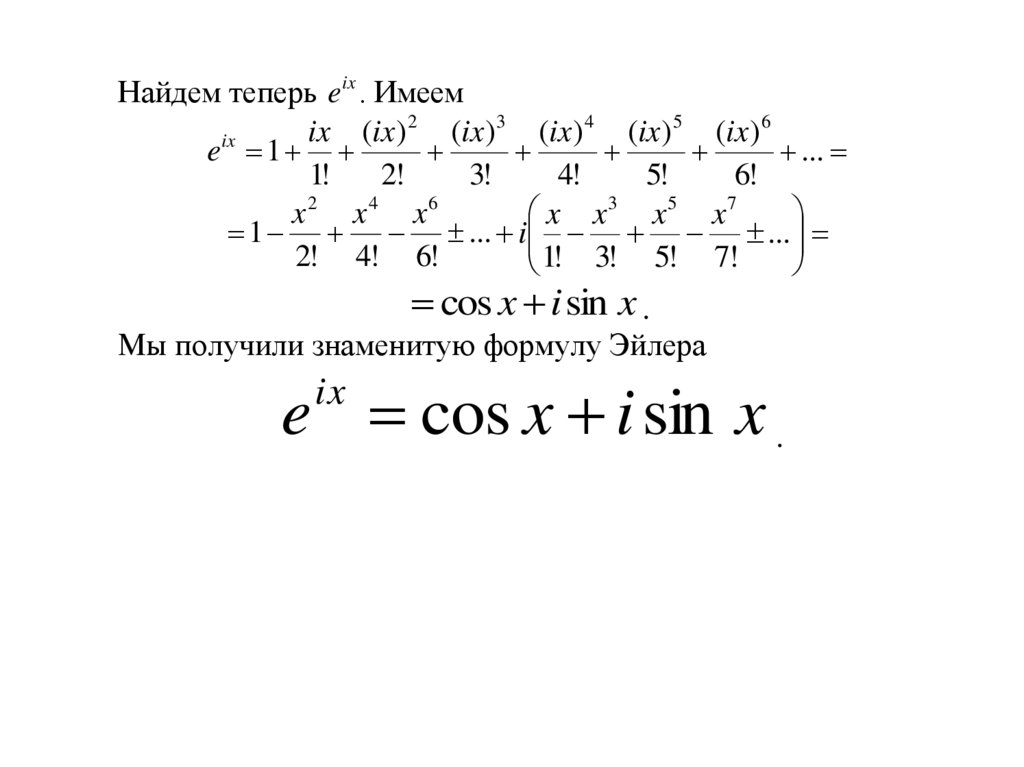



 mathematics
mathematics








