Similar presentations:
Комплексные числа
1.
§2. Комплексные числап.1. Основные понятия.
x 1
2
Комплексным числом называется выражение
вида
z x iy ,
где x, y R,
2
i — мнимая единица, i 1.
C — множество комплексных чисел.
Замечание 1.
Если x 0 , то число z iy называется чисто
мнимым.
Если y 0 , то z x R. Значит, R C.
2.
x Re z— действительная часть
комплексного числа;
y Im z
— мнимая часть комплексного
числа.
Два комплексных числа равны тогда и только
тогда, когда равны их действительные и
мнимые части.
z1 z2 Re z1 Re z2 , Im z1 Im z2
Замечание 2.
Для комплексных чисел не вводятся понятия
«больше» и «меньше».
3.
z x iy— число, комплексно сопряженное к
z x iy
Свойства
1) Re z 0 z z
2) Im z 0 z z
3) z z
z z
4) Re z
2
z z
5) Im z
2i
4.
Доказательство.Пусть
z x iy.
1) Необходимость.
Пусть Re z 0. Докажем, что z z .
Если Re z 0, то z iy , z iy , т.е.
z z.
Достаточность.
Пусть z z . Докажем, что Re z 0.
Имеем,
x iy ( x iy ) x iy x iy 0 2 x 0
Re z 0.
5.
4) Преобразуем левую часть:Re z x;
Преобразуем правую часть:
z z x iy x iy 2 x
x.
2
2
2
6.
п.2. Модуль и аргумент комплексногочисла.
M ( x, y)
y
O
x
Любое комплексное
число z
можно изобразить
точкой M ( x, y ) ,
такой, что
x Re z, y Im z.
Каждую точку M ( x, y ) можно рассматривать
как образ комплексного числа z x iy.
Плоскость называется комплексной.
Ось Ox — действительной осью.
Ось Oy — мнимой осью.
7.
M ( x, y)y
r
O
x
Любое комплексное
число z x iy
можно изобразить
радиус-вектором
r OM ( x, y).
Длина вектора r называется модулем
комплексного числа и обозначается
| z |, r , .
Угол между положительным направлением
действительной оси и вектором r называется
аргументом и обозначается Arg z.
8.
Значение аргумента, заключенное в границах(0 2 )
называют главным значением аргумента, и
обозначают arg z.
Arg z arg z 2 k , k Z
Аргумент комплексного числа z 0 не
определен.
Замечание 3.
| z1 | | z2 |,
z1 z2
arg z1 arg z2 .
9.
Связь между Re z, Im z и | z |, arg z.M
y
r
O
x r cos
y r sin
r x y
2
x
x
cos
r
y
sin
r
2
10.
Формы записи комплексных чиселАлгебраическая
z x iy
Тригонометрическая
x r cos
y r sin
z r (cos i sin )
Показательная (экспоненциальная)
i
Формула Эйлера: e cos i sin , R.
z re
i
11.
Замечание 4.i
e 1.
i
e cos i sin
Пример 1. Записать комплексное число
z 1 i
в тригонометрической и показательной форме.
Решение. Re z 1,
Im z 1.
| z | 1 ( 1) 2 ;
1
1
cos
, sin
, .
4
2
2
2
2
i
z 2 cos i sin 2e 4 .
4
4
12.
п.3. Действия над комплекснымичислами.
Пусть
z1 x1 iy1 ,
z2 x2 iy2 .
Сложение:
z1 z2 x1 x2 i y1 y2 .
z1
Неравенство треугольника:
| z1 z2 | | z1 | | z2 |
Пример 2.
z1 5 2i,
z2 3 i.
z1 z2 5 2i 3 i 8 i.
z1 z2
z2
13.
Вычитание:z1 z2 x1 x2 i y1 y2 .
z1
| z1 z2 | | z1 | | z2 |
Пример 3.
z1 5 2i,
z1 z2
z2
z2 3 i.
z1 z2 5 2i (3 i) 2 3i.
14.
Умножение:z1 z2 x1 x2 y1 y2 i x1 y2 y1 x2 .
z1 z2 ( x1 iy1 )( x2 iy 2 ) x1 x2 ix1 y2 iy1 x2 i 2 y1 y2
x1 x2 y1 y2 i x1 y2 y1 x2 .
Пример 4.
z1 5 2i,
z2 3 i.
z1 z2 (5 2i)(3 i) 15 5i 6i 2i 17 i.
Замечание 5.
2
z z | z | .
Доказательство.
2
z z ( x iy )( x iy ) x 2 ixy ixy i 2 y 2 x 2 y 2 | z |2 .
15.
Умножение комплексных чисел втригонометрической форме.
Пусть
z1 r1 (cos 1 i sin 1 ), z2 r2 (cos 2 i sin 2 ).
Тогда
z1 z2 r1 (cos 1 i sin 1 )r2 (cos 2 i sin 2 )
r1r2 (cos 1 cos 2 i cos 1 sin 2 i sin 1 cos 2 i 2 sin 1 sin 2 )
r1r2 (cos 1 cos 2 sin 1 sin 2 ) i(cos 1 sin 2 sin 1 cos 2 )
r1r2 (cos( 1 2 ) i sin( 1 2 ) .
z1 z2 r1r2 (cos( 1 2 ) i sin( 1 2 ) .
При умножении комплексных чисел их модули
перемножаются, а аргументы складываются.
16.
Можно показать, чтоz1 z2 ...zn r1r2 ...rn (cos( 1 2 ... n ) i sin( 1 2 ... n ) .
Если
то
z1 z2 ... zn r (cos i sin ),
z r (cos n i sin n )
n
n
— формула Муавра.
Пример 5. Вычислить
(1 i) .
Решение.
1 i 2 cos i sin .
4
4
20
10
10
(1 i) 2 cos 5 i sin 5 2 1024.
20
17.
Деление: zx1 x2 y1 y2
y1 x2 x1 y2
1
i 2
.
2
2
2
z2
x2 y 2
x2 y 2
z1 x1 iy1 x1 iy1 x2 iy 2 x1 x2 ix1 y2 ix2 y1 i 2 y1 y2
2
2
z2 x2 iy 2 x2 iy 2 x2 iy 2
x2 y2
x1 x2 y1 y2 i( y1 x2 x1 y2 ) x1 x2 y1 y2
y1 x2 x1 y2
i 2
.
2
2
2
2
2
x2 y 2
x2 y2
x2 y 2
Пример 6.
5 2i (5 2i)(3 i) 15 5i 6i 2i 13 11i 13 11
i.
3 i
(3 i)(3 i)
9 1
10
10 10
2
18.
Деление комплексных чисел втригонометрической форме.
Пусть
z1 r1 (cos 1 i sin 1 ), z2 r2 (cos 2 i sin 2 ).
Тогда
z1 r1 (cos 1 i sin 1 ) r1 (cos 1 i sin 1 )(cos 2 i sin 2 )
z2 r2 (cos 2 i sin 2 ) r2 (cos 2 i sin 2 )(cos 2 i sin 2 )
r1 cos 1 cos 2 i cos 1 sin 2 i sin 1 cos 2 i 2 sin 1 sin 2
2
2
r2
cos 2 sin 2
r1
(cos 1 cos 2 sin 1 sin 2 ) i(sin 1 cos 2 cos 1 sin 2 ) ,
r2
z1 r1
cos( 1 2 ) i sin( 1 2 ) .
z2 r2
При делении комплексных чисел их модули
делятся, а аргументы вычитаются.
19.
Извлечение корня из комплексных чиселПусть n N, n 2.
Корнем n-й степени из комплексного числа z
называется комплексное число w,
удовлетворяющее равенству
w z.
n
Пусть
z r (cos i sin ),
w (cos i sin ).
Тогда
n (cos n i sin n ) r (cos i sin ).
20.
Учитывая замечание 3, получаемr r;
n
n
2 k
n 2 k , k Z
, k Z.
n
Поэтому,
n
2 k
2 k
r (cos i sin ) r cos
i sin
,
n
n
n
k 0,1,..., n 1.
Получили n различных значений корня n-й
степени из комплексного числа.
21.
Пример 7. Найти все значения 4 1.Решение.
Представим комплексное число в z 1
тригонометрической форме
z 1 1(cos 0 i sin 0).
Тогда
4
0 2 k
0 2 k
1 1 cos
i sin
, k 0,1,2,3.
4
4
4
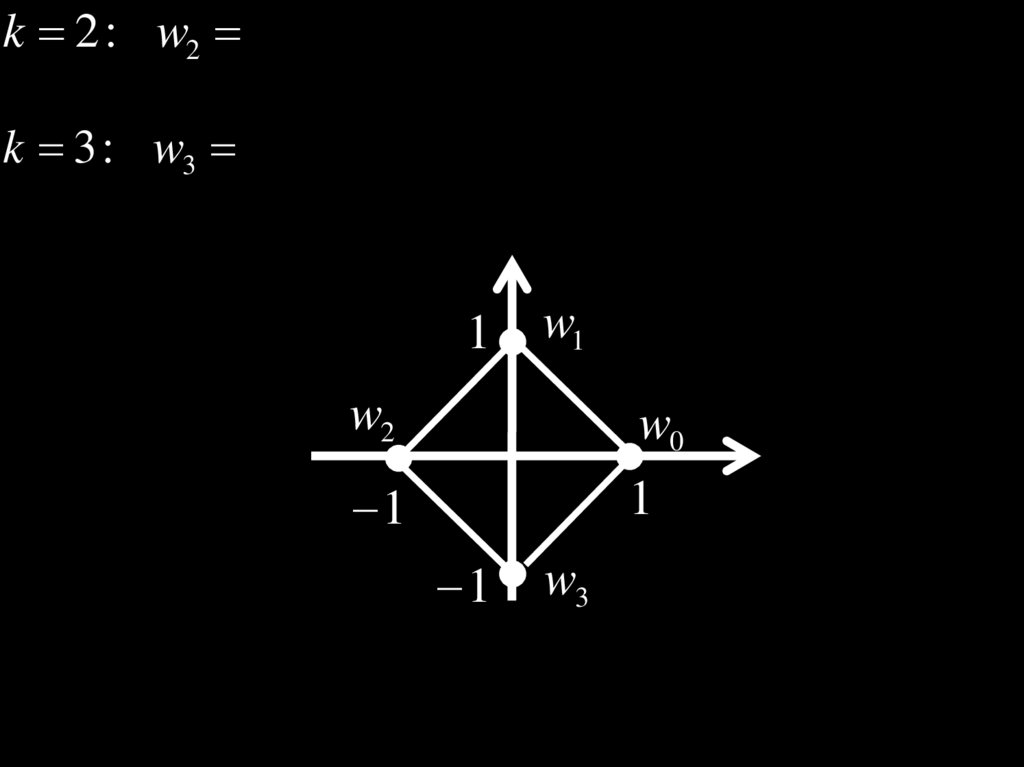
k 0 : w0 cos 0 i sin 0 1;
k 1 : w1 cos i sin i;
2
2
22.
k 2 : w2 cos i sin 1;3
3
k 3 : w3 cos
i sin
i.
2
2
1
w1
w2
w0
1
1
1
w3
















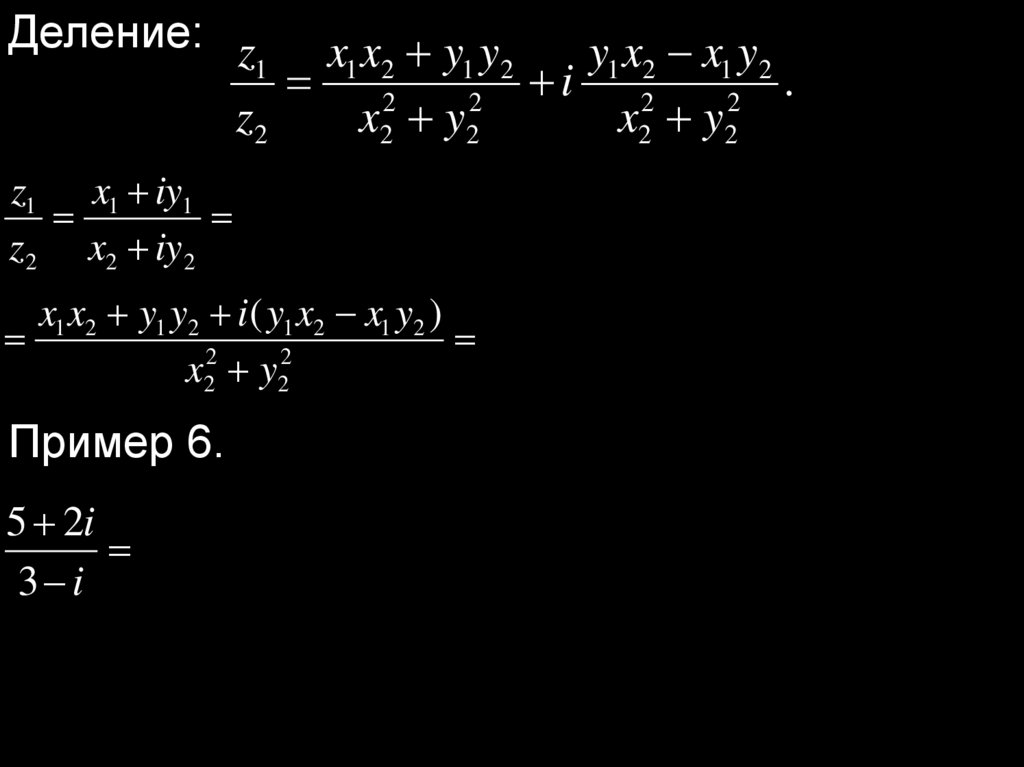




 mathematics
mathematics








