Similar presentations:
Теория поверхностей. Нормальная кривизна линии на поверхности. Вторая квадратичная форма поверхности
1. ТЕОРИЯ ПОВЕРХНОСТЕЙ
Нормальная кривизналинии на поверхности.
Вторая квадратичная
форма поверхности
2. Нормальная кривизна линии на поверхности. Вторая квадратичная форма
Определение: проекция вектора кривизны кривой, лежащей наповерхности, на нормаль к поверхности в данной
точке кривой называется нормальной кривизной
кривой.
Пусть кривая на поверхности задана уравнением: r r (u ( s); v( s))
r - вектор кривизны кривой;
N [ru ; rv ] – вектор нормали к поверхности,
n
N
[r ; r ]
u v
| N | | [ ru ; rv ] |
[ ru ; rv ]
EG F 2
(15) – единичный вектор нормали.
r ru u rv v
ru ru (u(s), v(s))
rv rv (u (s), v( s))
(15)
3. Нормальная кривизна линии на поверхности. Вторая квадратичная форма
ru ruuu ruvv2r
ruu 2
u
rv ruvu rvv v
об
2r
ruv
u v
об
2r
rvv 2
v
об
r ru u ru u rv v rv v ruu u 2 ruv u v ru u rvu u v rvv v 2 rv v
ruu u 2 2ruv u v rvv v 2 ru u rv v
k n - нормальная кривизна кривой на поверхности.
k n прn r n r ruu n u 2 2ruv n u v rvv n v 2 ru n u rv n v
ru n rv n 0
k n ruu n u 2 2ruv n u v rvv n v 2
4. Нормальная кривизна линии на поверхности. Вторая квадратичная форма
обL ruu n
об
M ruv n
об
N rvv n
(16)
Учитывая обозначения (16) получим:
k n Lu 2 2Mu v Nv 2 ,
du
, тогда
и учтем, что u
ds
Ldu 2 2 Mdudv Ndv 2 Ldu 2 2Mdudv Ndv 2 2
kn
2
2
2
1
ds
Edu 2 Fdudv Gdv
2 Ldu 2 2Mdudv Ndv 2
(18) – формула второй квадратичной формы поверхности.
(17)
(18)
5. Вычисление коэффициентов второй квадратичной формы
ruu ru rvL
EG F 2
ruv ru rv
M
EG F 2
rvv ru rv
N
EG F 2
(19)
С другой стороны, ru n rv n 0, продифференцируем по u
0 ( ru n ) u ruun ru nu
L ru nu
M ru nv rv nu
N r n
v v
(20)
6. Вычисление коэффициентов второй квадратичной формы
2 ru nu du 2 ru nv dudv rv nu dvdu rv nv dv 2 (ru du rv dv)( nu du nv dv)2 drdn ,
так как dr ru du rv dv,
(21)
dn nu du nv dv.
Утверждение 2.
Нормальные кривизны двух кривых на поверхности, проходящих
через точку Р и имеющих в этой точке общую касательную, в
точке Р равны между собой.
Доказательство:
2
dv
dv
L 2M
N
2
2
2
|: du
Ldu 2 Mdudv Ndv
du
du
kn
2
Edu 2 2 Fdudv Gdv 2 |: du 2
dv
dv
E 2F
G
du
du
7. Вычисление коэффициентов второй квадратичной формы
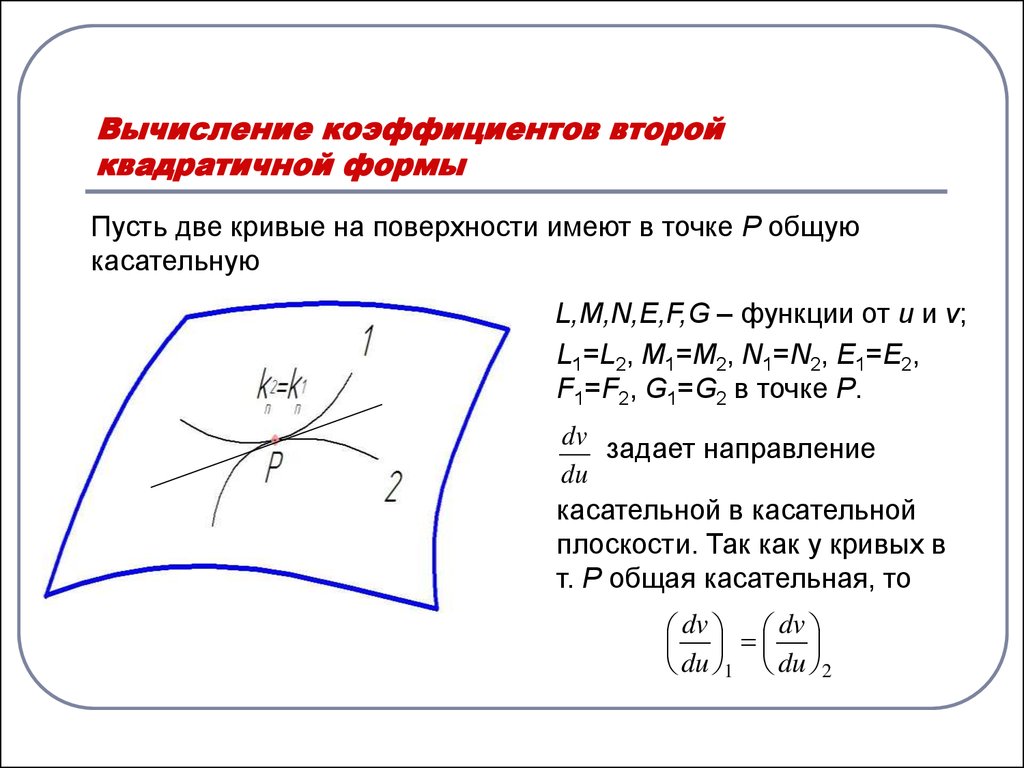
Пусть две кривые на поверхности имеют в точке P общуюкасательную
L,M,N,E,F,G – функции от u и v;
L1=L2, M1=M2, N1=N2, E1=E2,
F1=F2, G1=G2 в точке Р.
dv задает направление
du
касательной в касательной
плоскости. Так как у кривых в
т. P общая касательная, то
dv dv
du 1 du 2
8. Вычисление коэффициентов второй квадратичной формы
в этой точке, следовательно:k n1 k n2 .
Ч.т.д.
Определение: нормальная кривизна кривой на поверхности в
данной точке называется нормальной кривизной
поверхности в данной точке в данном
направлении касательной плоскости.







 mathematics
mathematics