Similar presentations:
Оптимизация деталей ГТД
1. ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования
МОСКОВСКИЙ ФИЗИКО-ТЕХНИЧЕСКИЙ ИНСТИТУТ(государственный университет)
Оптимизация деталей ГТД
________________________________________________________
Бакалаврская диссертация студента 865 группы ФАЛТ
Калинчевой Марии Викторовны
Научный руководитель: доктор технических наук, профессор
Темис Юрий Моисеевич
Москва, 2012
2.
План•Постановка задачи:
вывод основных уравнений;
метод чувствительности на примере задачи оптимизации диска
методы расчета диска
•Описание программного комплекса
•Результаты расчетов
•Заключение
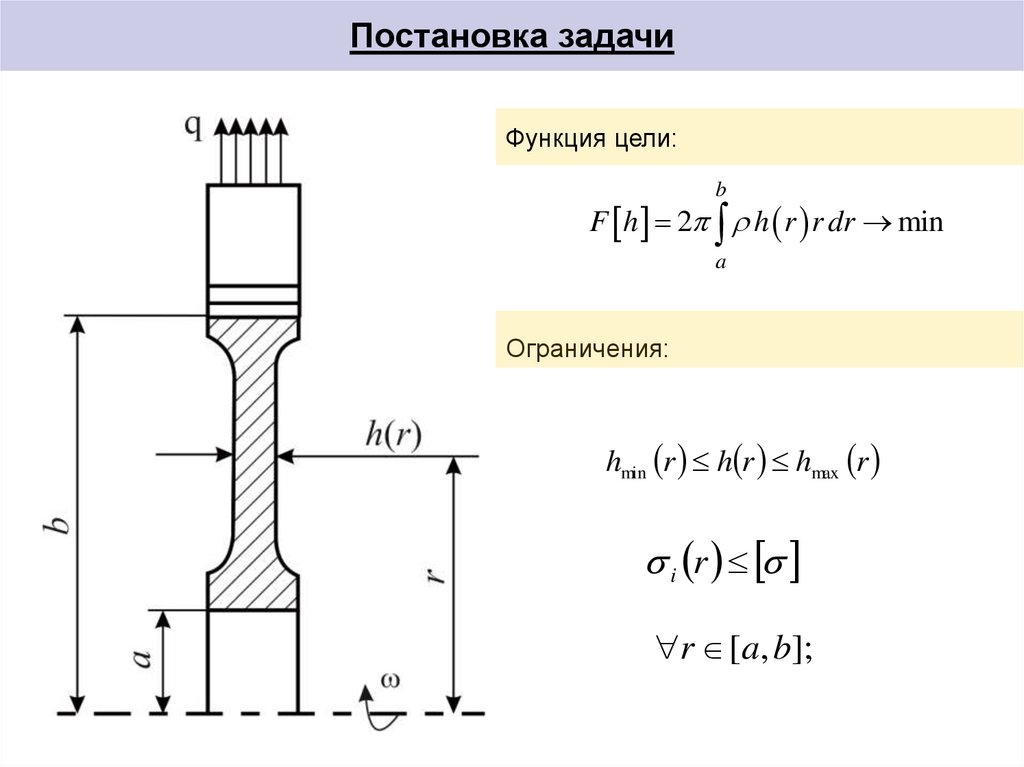
3. Постановка задачи
Функция цели:b
F h 2 h r r dr min
a
Ограничения:
hmin r h r hmax r
i r
r [a, b];
4. Вывод основных уравнений равновесия диска
Равновесие элемента диска:N r rd ( N r dN r )( r dr )d 2 N dr sin
d
2 hr 2 drd 0
2
dN r 1
( N r N ) 2 hr 0
dr r
Уравнение равновесия в перемещениях:
(1 2 ) 2r
E d
dh
d 2u 1
1 dh du dh 1
T
T
u
2
2
E
1
dr
dr
r
h
(
r
)
dr
dr
rh
(
r
)
dr
dr
r
Q r hr
du
1 2 1
u
Q 1 T
dr
r
Er h
1 u a 1Q a 1
dQ E
hu Q E T 2 r 2 h .
dr r
r
2 u b 2 Q b 2
5. Метод чувствительности на примере задачи оптимизации вращающегося диска
Исходная задача:Вариация толщины:
u (1 )
Q E T qr r h
h2 r h1 r v r
b
F1 h Ф1 u, Q, h, r dr
a
2 u b 2Q b 2
b
b
a
a
F v 2 r v dr wv dr
2
r
и
1 dr 0
a
2
1 u a 1Q a 1
f1
u h
J h 0
Q f 2
h
h1 r
J
b
Уравнение в вариациях:
w 2 r
b
Ф
Ф
Ф
F1 v 1 u 1 Q 1 v dr
u
Q
h
a
1 u a 1 Q a 0
2 u b 2 Q b 0
b
b
f1
x
J
dr
a
T
*
a
h
f2
hdr 0
h
Сопряженная задача:
Ф1
u
* 1
J
2
Ф1
Q
d
dr r
*
J
2
1
Erh
1 1 a 1 2 a 0
2 1 b 2 2 b 0
b
f1
f2
Ф1
F1 v
1
2
v r dr w1 r v r dr
h
h
h
a
a
b
Eh
r
d
dr r
1
f 1 f 2 Ф1
w1 r
,
,
2
h
h
h
1
6. Метод чувствительности на примере задачи оптимизации вращающегося диска
Задача нахождения минимума линейного функционала:b
b
b
a
a
F h1 F v 2 h1 r rdr w r v r dr C w r v r dr min,
a
b
F1 h1 w1 r v r dr 0,
a
b
2
v
r
dr
0,
2
a
b
ww1dr
1
F1
a
v r w b
w1 b
w1
2
2
w
dr
w
dr
1
1
a
a
7. Методы расчета диска
МКЭМКР
u (b)
Q (b)
u c1
R
J Q c2 dr 0
a
a
b
N
e 1
e 1
e
b
N
e 1
e 1
e
N
e 1
e 1
e
(1)
T
(0)
M e 4 4 M1 4 4 M 2 4 4
u
T
Q
u (b)
Q(b)
1
0
c1 0
c2 0
T
N N dr T N D N dr T N f dr
T
(2)
0
1
u (b)
Q(b)
c1 (1 )
c2 E T qr r h
0
0
Общее решение системы:
u u (r )
Q Q(r )
(0)
u (r )
Ck
Q(r )
k 1
2
(k )
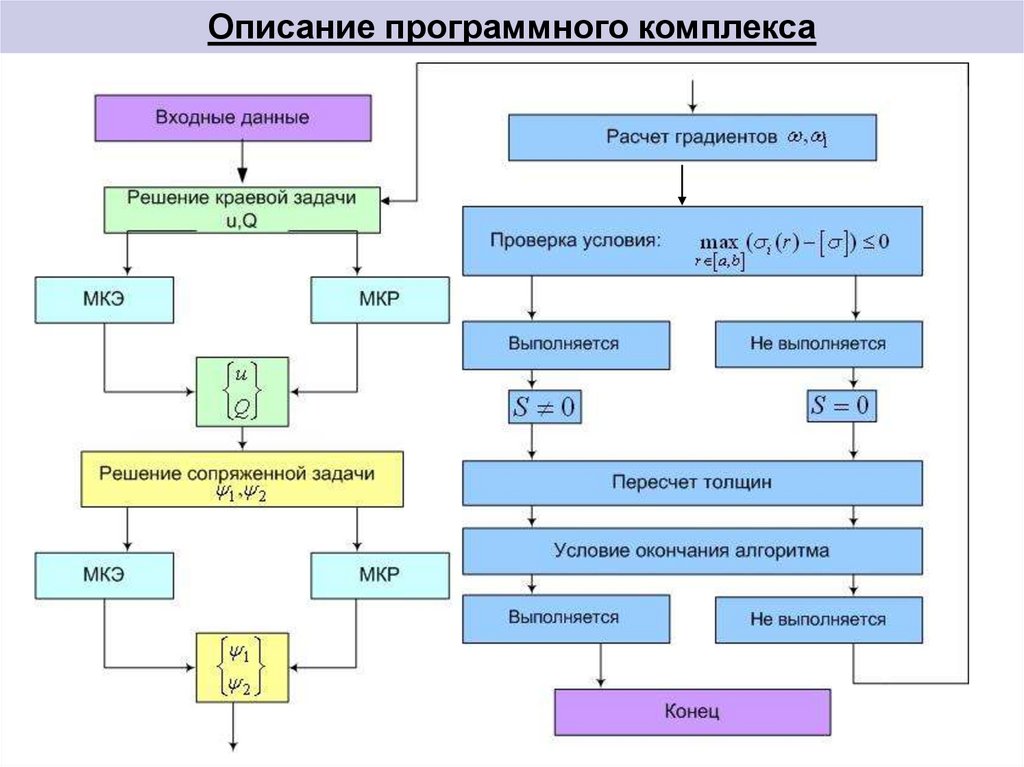
8. Описание программного комплекса
9. Результаты расчетов
Равнопрочный диск:Аналитическое решение
h(r ) hc
2 2 2
(c r )
2
e
Параметры диска
Ra 0 м
Rb 0.22 м
500 рад / c
E 201ГПа
8300кг / м3
0.28
h0 0.04 м
аналитическое решение
расчетное решение
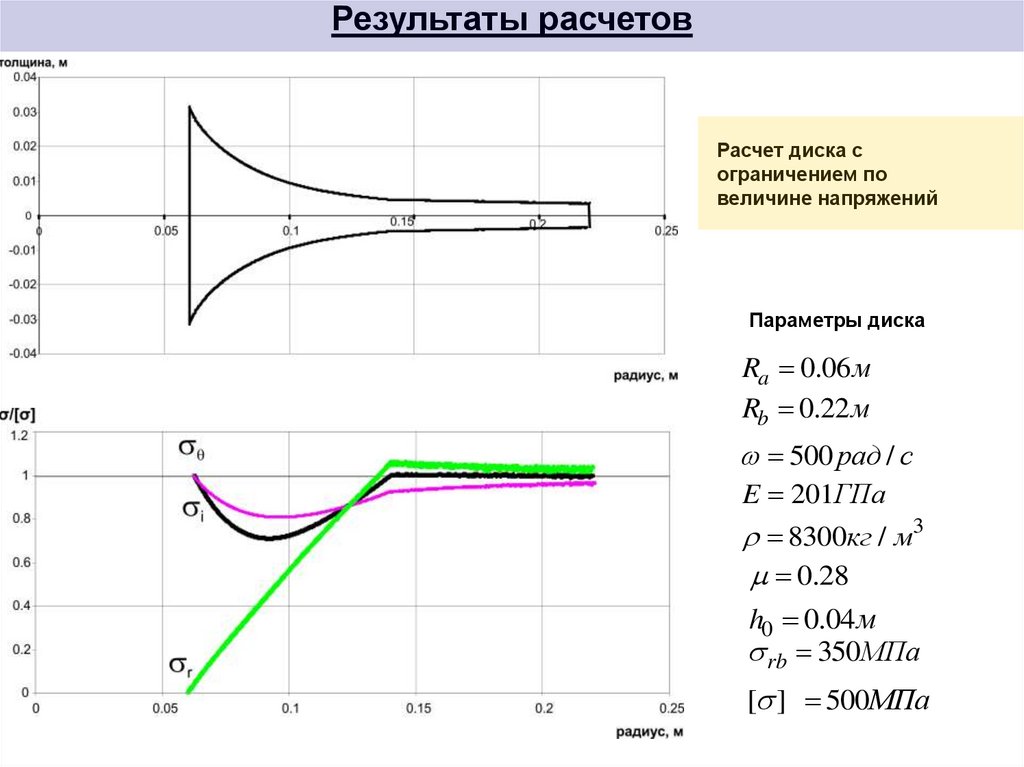
10. Результаты расчетов
Расчет диска сограничением по
величине напряжений
Параметры диска
Ra 0.06 м
Rb 0.22 м
500 рад / c
E 201ГПа
8300кг / м3
0.28
h0 0.04 м
rb 350МПа
[ ] 500МПа
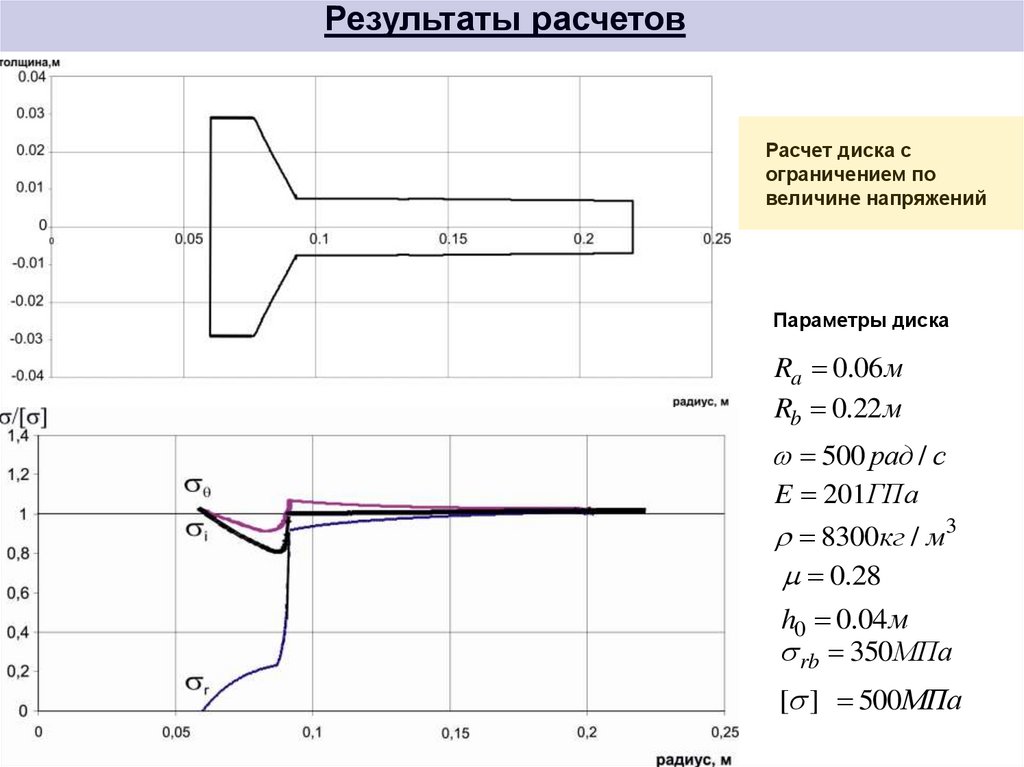
11. Результаты расчетов
Расчет диска сограничением по
величине напряжений
Параметры диска
Ra 0.06 м
Rb 0.22 м
500 рад / c
E 201ГПа
8300кг / м3
0.28
h0 0.04 м
rb 350МПа
[ ] 500МПа
12. Заключение
•Решена задача оптимизации вращающегосяосесимметричного диска методом чувствительности, что
позволило сократить время расчета в задаче оптимального
проектирования.
•Реализован алгоритм метода чувствительности, метода
конечных элементов и метода конечных разностей.
•Решена задача оптимизации диска методом
чувствительности с введением дополнительных
ограничений на максимальную (или минимальную) ширину
диска.
•В ходе выполнения работы написаны программы метода
чувствительности для оптимизации диска.









 physics
physics








