Similar presentations:
Замедление нейтронов
1. Замедление нейтронов
В лабораторной системе координат:n
V2
− ядро покоится (V=0),
V1
− нейтрон летит со скоростью V1
n
A
A
В системе координат центра инерции:
− ядро летит со скоростью Vm,
n
Va
− нейтрон летит со скоростью V1- Vm
V1-Vm
n
Vm
Vb
A
A
2.
В лабораторной системе координат импульс равен:I 1 V1
В системе координат центра инерции:
1 (V1 Vm ) A Vm 0
Vm – скорость центра инерции
в лабораторной системе координат
V1
ядро летит навстречу нейтрону со скоростью - Vm
,
( A 1)
A V1
а нейтрон навстречу ядру со скоростью V1 Vm
( A 1)
После столкновения:
скорость нейтрона – Va
скорость ядра отдачи – Vb
3.
Закон сохранения импульса1 Va A Vb 0 или 1 Va A Vb
Закон сохранения энергии
2
2
1 A V1
A V1
1 2 1
2
V
A
V
a
b
2 A 1 2 A 1
2
2
Решая получаем
A V1
Va
;
A 1
V1
Vb
A 1
4.
Переходя к лабораторной системе координатV2
Va
Первоначальное движение нейтрона
Vm
V22 Vm2 Va2 2 Vm Va cos Θ
2
2
V
(A
2 A cos Θ 1)
2
1
V2
( A 1) 2
Т.е.
E2 V22 A2 2 A cos Θ 1
2
E1 V1
( A 1) 2
5.
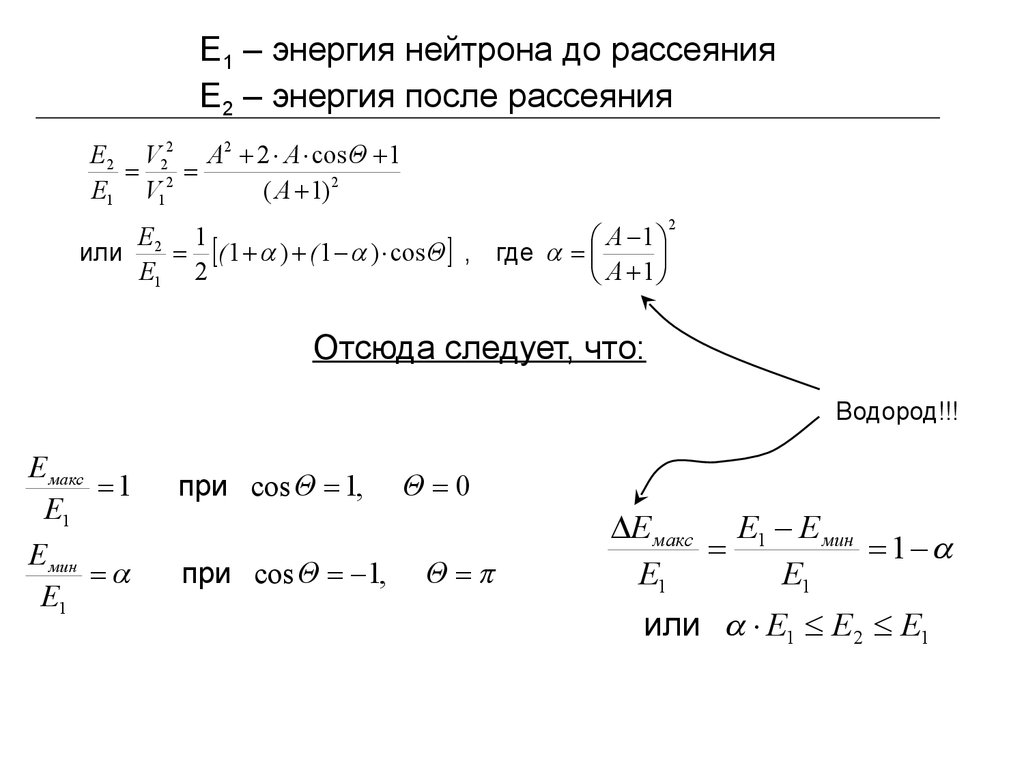
E1 – энергия нейтрона до рассеянияE2 – энергия после рассеяния
E2 V22 A2 2 A cos Θ 1
E1 V12
( A 1) 2
E
1
A 1
или 2 ( 1 ) ( 1 ) cos Θ , где
E1 2
A 1
2
Отсюда следует, что:
Водород!!!
E макс
1
E1
при cos Θ 1,
E мин
E1
при cos Θ 1,
Θ 0
Θ
E макс E1 E мин
1
E1
E1
или E1 E2 E1
6.
При энергиях ниже нескольких Мэв упругое рассеяние сферически симметрично.Поэтому справедливо соотношение:
dO
p(Θ)dΘ
dO 2 π sin ΘdΘ 1
sin ΘdΘ
4
4π
2
Θ
dΘ
p(E2 )dE2 - вероятность того что после рассеяния
энергия нейтрона будет лежать в интервале - E2 E2 dE2
p(E2 )dE2 p(Θ)
dΘ
dE2
dE2
Поскольку
E2 1
( 1 ) ( 1 ) cos Θ , то
E1 2
dΘ
2
,
dE2
E1 ( 1 α) sin Θ
следовател ьно
p(E2 )dE2
dE2
E1 ( 1 α)
Разумеется
E1
1
p
(
E
)
dE
2 2 E1 (1 )
E1
E1
dE
E1
2
1
7. Средний логарифм потери энергии при одном столкновении
E1E
ln 1
E2
E1
E
ln 1 p( E2 )dE2
E2
E1
p( E )dE
2
2
E1
E1
E1
dE2
ln
E2 E1 (1 )
E1
Интегрируя получим:
Поскольку это равно 1 , а это равно
α
1
α
ξ
ln (x)dx 1
ln α
1 α 1
1 α
dE2
E1 (1 )
E2
(замена переменной x )
E1
( A 1) 2 A 1
или 1
ln
, при A 10
2A
A 1
2
A 2/3
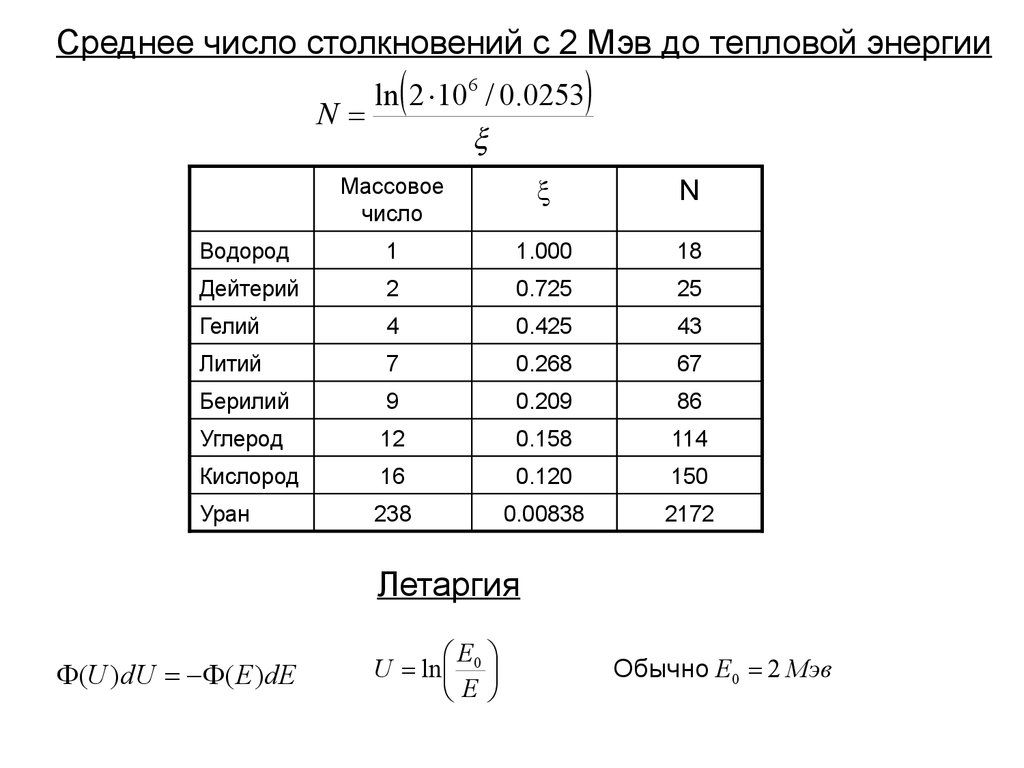
8. Среднее число столкновений с 2 Мэв до тепловой энергии
ln 2 106 / 0.0253N
Массовое
число
N
Водород
1
1.000
18
Дейтерий
2
0.725
25
Гелий
4
0.425
43
Литий
7
0.268
67
Берилий
9
0.209
86
Углерод
12
0.158
114
Кислород
16
0.120
150
Уран
238
0.00838
2172
Летаргия
(U )dU ( E )dE
E
U ln 0
E
Обычно E0 2 Мэв
9.
Спектр замедляющихся нейтронов в системе без поглощения(рассеяние на водороде, А=1, =0, =1)
Q(E0)
dE
dE'dE'
( E ) s ( E )dE - число актов рассеяния в 1 сек в 1 см3 при энергии Е в интервале dE
F ( E ) ( E ) s ( E ) - плотность столкновен ий
Поскольку
Доля нейтронов рассеянных в интервал dE
в результате рассеяния в dE'
F ( E )dE
dE
Полное число нейтронов рассеянных в интервал dE
в результате предшествующего рассеяния
dE
E
p(E2 )dE2
dE2
E1 ( 1 α)
E0
F ( E )dE
E E dE
(1)
Кроме этого, источник даёт Q нейтронов в 1 сек в 1 см3 с энергией Е0
и полное число нейтронов рассеянных в интервал dE
в результате первого столкновения
Q
dE
E0
(2)
Условие стационарности - F(E) dE = (1) + (2)
(сколько рассеялось в интервал dE, столько и ушло из этого интервала
в результате рассеяния, поскольку поглощение отсутствует)
10.
Спектр замедляющихся нейтронов в системе без поглощения(рассеяние на водороде, А=1, =0, =1)
Q
F (E)
E0
Продифференцировав по E, получим
E0
F ( E )
E E dE
dF ( E )
F (E)
const
. Решение F ( E )
dE
E
E
Граничное условие – очевидно: F ( E0 ) Q .
Следовател ьно,
E0
Поскольку,
F ( E ) ( E ) S ( E ) , т
(3)
( E )
const Q,
Q
E S (E)
и
( E )
F (E)
Q
E
Q
S E
В общем случае при А > 1, можно показать, что
( E )
Q
S E
(4)
(для водорода =1)
11.
Плотность замедления(на водороде, А=1, =0, =1)
- q
q - число нейтронов в 1см3 в 1 сек пересекающих
при замедлении значение энергии E
Плотность столкновений при энергии E' в интервале dE'
F ( E )dE S ( E ) ( E )dE
Доля нейтронов пересекающих Е при столкновении при энергии E'
E0
Число нейтронов замедляющихся за энергию E
в результате предшествующего рассеяния
число нейтронов рассеянных за энергию E
в результате первого столкновения
E
E
Q E
E0
F ( E )
dE
E
E
E
(5)
(6)
E
Следовательно, - q = (5) + (6)
В среде без поглощения плотность замедления не зависит от энергии
т.е.
E
0
0
Q E
F ( E )
Q E
dE
E
dE
Q E 2 Q
E0
E
E0
E
E
E
q=Q
12.
(E)q
Е
13.
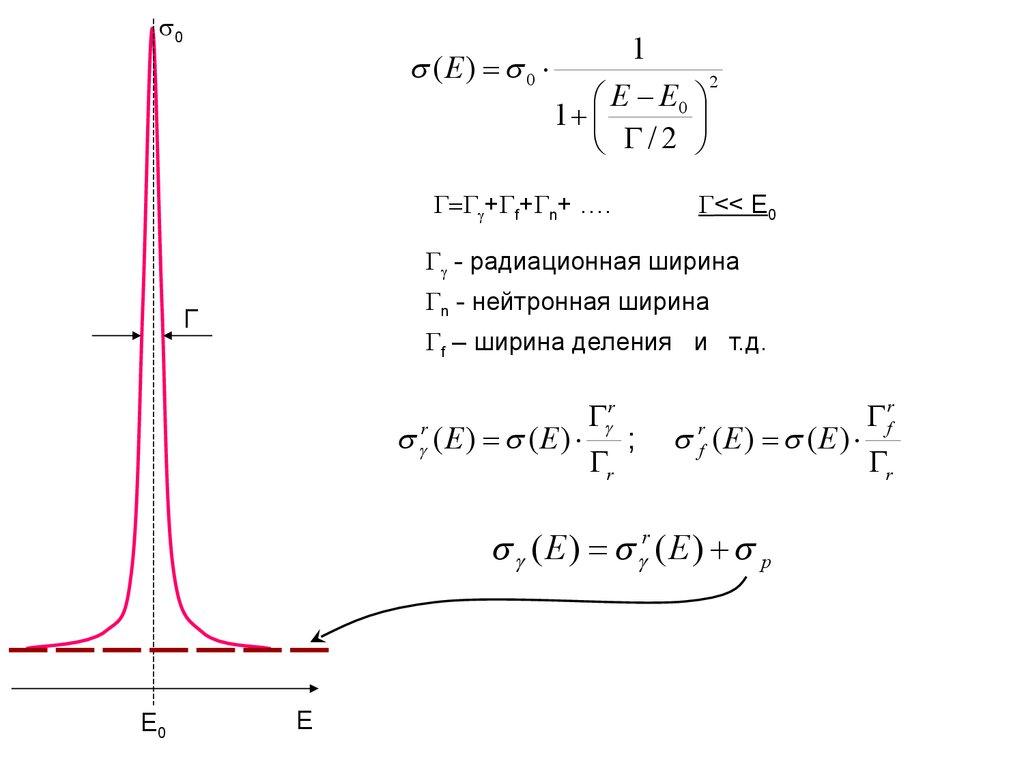
0(E) 0
1
E E0
1
/2
+ f+ n+ ….
2
<< E0
- радиационная ширина
n - нейтронная ширина
Г
f – ширина деления и т.д.
r
r ( E ) ( E ) ;
r
rf ( E ) ( E )
( E ) r ( E ) p
E0
E
fr
r
14.
Резонансный интеграл поглощения1
I ( E ) ( E )dE ( E ) dE
E
E
E
r
1
I ar I r
r ( E ) r dE
Если << Er , то
Er E
r
a
Гr
r
a
r
a
r
0r r
1 0r r
1
r
dx
;
2
Er
2
1 x
2 Er
Ф(E) 1/Е
Полный резонансный интеграл
n
I I1 I 2 .... I N I r
r 1
r
x
E E0
Γ/ 2
15.
Резонансный интеграл "бесконечного разбавления“(резонансный интеграл в невозмущённом спектре Ферми)
I a I ar
r
Изотоп
I , барн
Ag109
In115
Au197
Th232
U238
1160
2640
1558
83
280
16.
(E)q
qr
qr-1
Еr-1
qr+1
Еr
Е
Еr+1
Вероятность избежать захвата на r-ом резонансе -
qr 1
1
qr
r
17.
Баланс нейтронов в окрестности r-го резонансаqr 1 a ( E ) ( E )dE qr
E
qr 1 E
qr
a
( E ) ( E )dE
qr
1 ;
r Pr 1
Если Pr не велико по сравнению с 1, то
1 P
r
r
P
e
r
r
P
e
Вероятность избежать захвата на всех резонансах -
r e
r
Pr
r
18.
ТопливоЗамедлитель
19.
20.
21.
22.
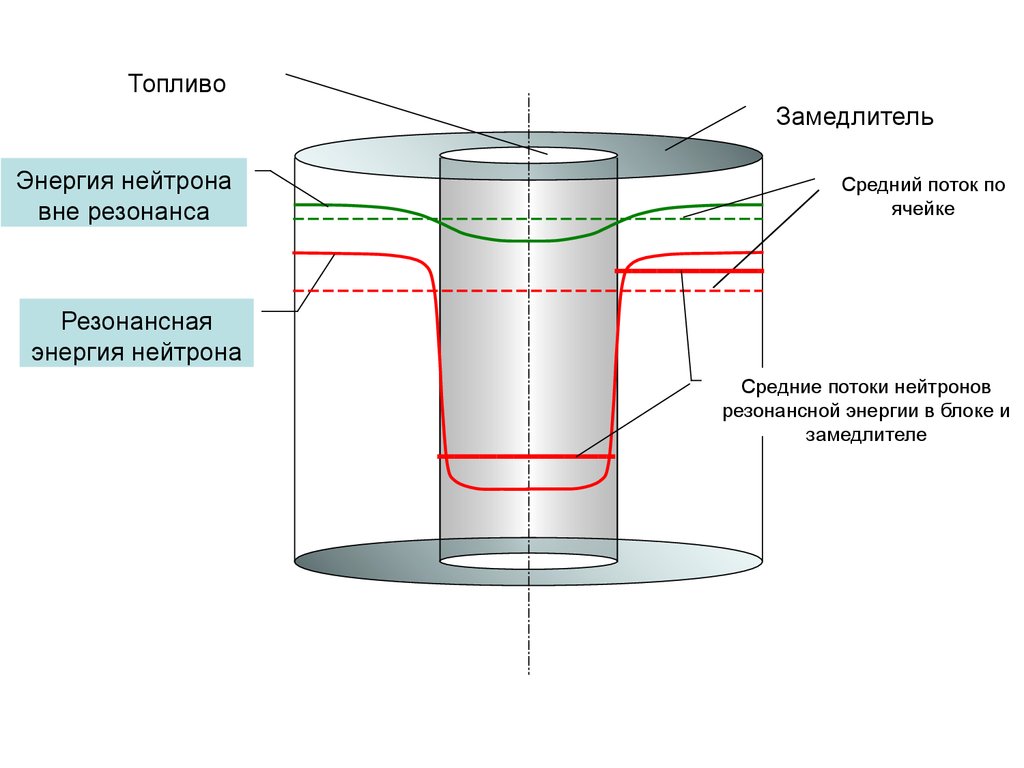
ТопливоЗамедлитель
Энергия нейтрона
вне резонанса
Средний поток по
ячейке
Резонансная
энергия нейтрона
Средние потоки нейтронов
резонансной энергии в блоке и
замедлителе
23.
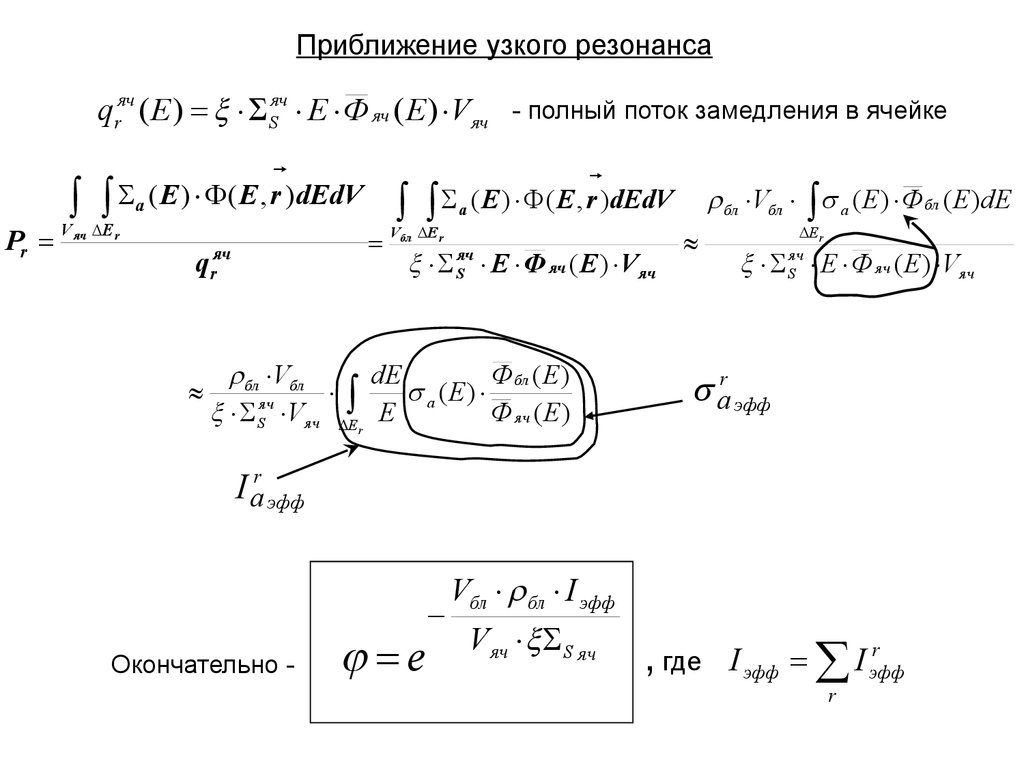
Приближение узкого резонансаqrяч ( E ) Sяч E Ф яч ( E ) Vяч - полный поток замедления в ячейке
Pr
(
E
)
(
E
,
r
)dEdV
a
V яч E r
qrяч
(
E
)
(
E
,
r
)dEdV
a
Vбл E r
Sяч E Ф яч ( E ) V яч
бл Vбл
dE
Ф бл ( E )
(
E
)
Sяч Vяч Er E a
Ф яч ( E )
бл Vбл a ( E ) Ф бл ( E )dE
E r
яч
S
E Ф яч ( E ) Vяч
ar эфф
I ar эфф
Окончательно -
e
Vбл бл I эфф
Vяч S яч
, где
r
I эфф I эфф
r
24.
Эффективный резонансный интеграл поглощенияI эфф
- зависит от температуры и вида гетерогенности
1. Гомогенная среда
2. Одиночный цилиндрический
блок в замедлителе
I эфф
S
3.8
U
S
M
I эфф A B
A
B
Uмет
3.1
26.8
UO2
4.45
26.3
UC
5.90
26.2
Thмет
1.83
15.5
ThO2
2.63
16.2
ThC
3.43
16,9
0.42
,
S см2 , M граммы
25.
Эффективный резонансный интеграл поглощения3. КластернаяТемпературная
структура
зависимость резонансного интеграла
I эфф
S out C1 Sin C2
A B
, С1 и С2 – поправки
Данкова
S
T T0
I эфф (T ) I эфф (T0 ) M
1 At Bt
4. «Теорема эквивалентности»
1 С
l бл
M
, С – поправка Данкова
0.005
UO2
0.0058
0.005
UC
0.0058
0.005
Thмет
0.009
0.0
ThO2
0.015
0.0
ThC
0.015
0.0
мет
*
P
Bt
бл At
P
0.0051
I эфф (T , ) , U
*
P


















 physics
physics








