Similar presentations:
Измерительные работы
1.
26.01. Измерительные работы2.
3.
4.
5.
6.
7.
8.
9. Сумма углов треугольника
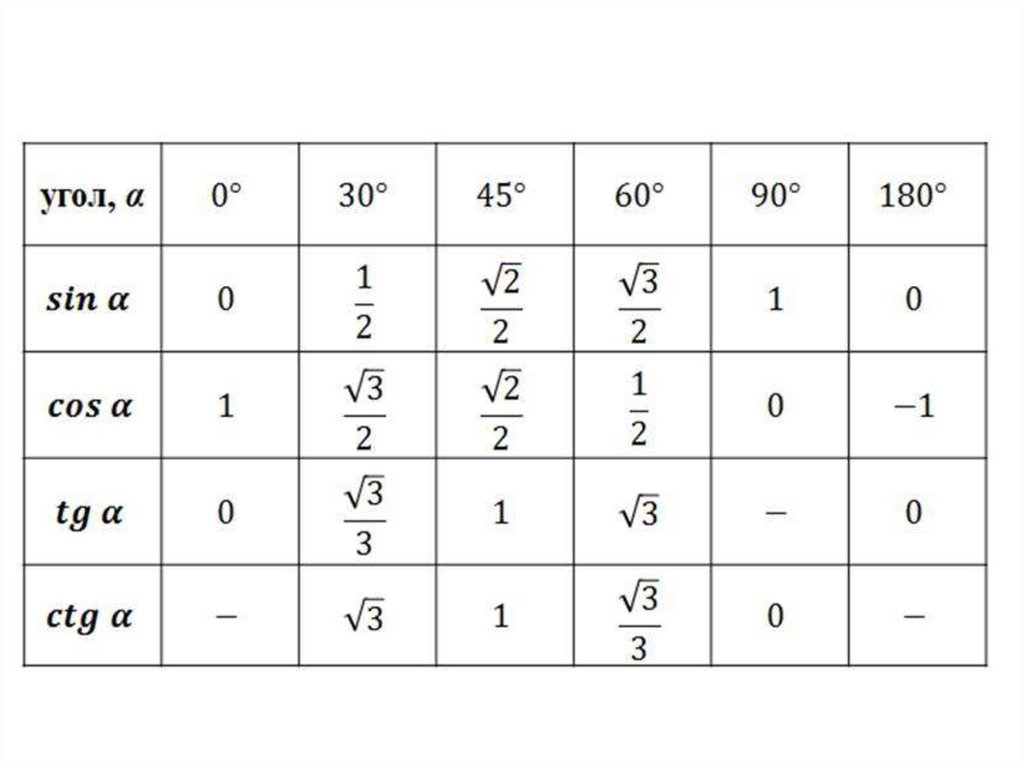
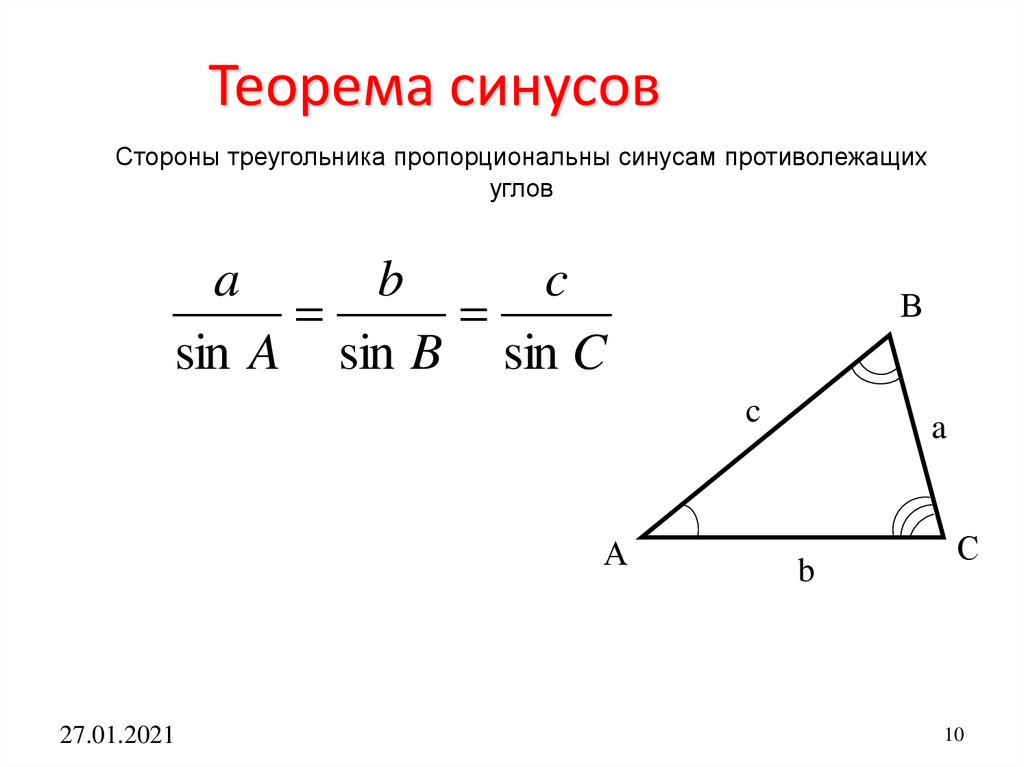
Теорема синусовСтороны треугольника пропорциональны синусам противолежащих
углов
a
b
c
sin A sin B sin C
В
c
А
1027.01.2021
a
b
С
10
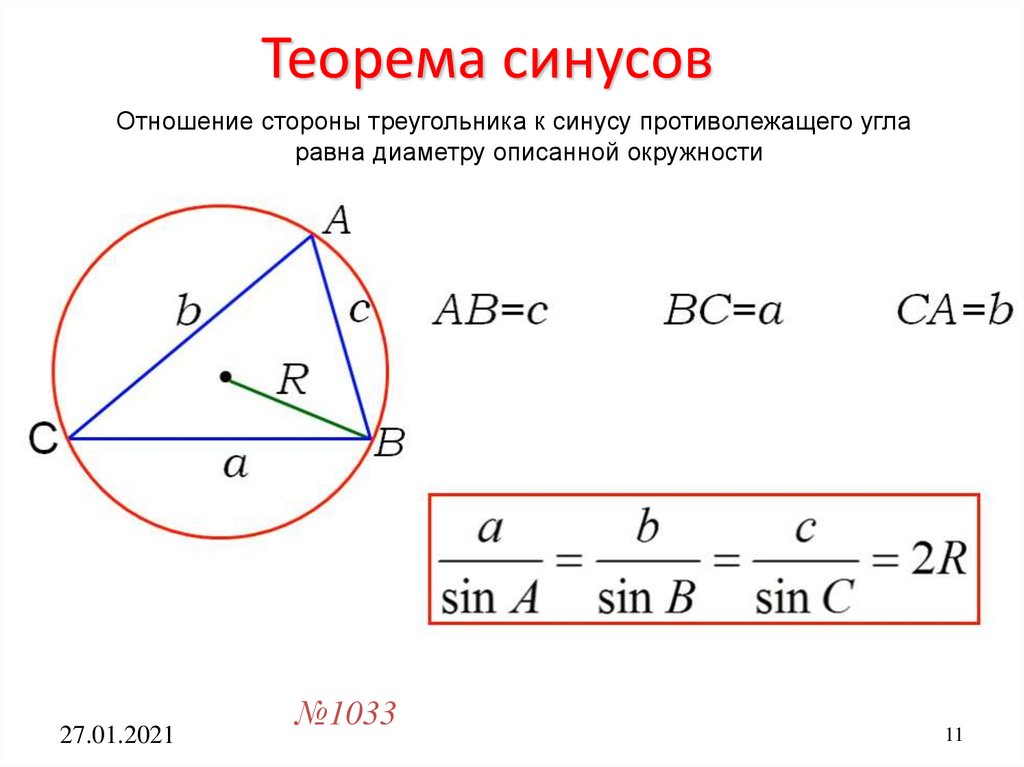
10. Теорема синусов
Отношение стороны треугольника к синусу противолежащего угларавна диаметру описанной окружности
27.01.2021
№1033
11
11.
Теорема косинусовКвадрат стороны треугольника равен сумме
квадратов двух других сторон минус
удвоенное произведение этих сторон на
косинус угла между ними.
a b c 2bc cos A
2
2
2
А
1227.01.2021
В
c
a
b
С
12
12. Теорема косинусов
Зачем нужны эти задачи?В Древней Греции, наряду с блестящим
развитием теоретической геометрии,
научных методов исследования и
логических доказательств, большое
значение имела прикладная геометрия.
Римляне вообще занимались лишь одной
практической и прикладной стороной
математики, необходимой лишь для
землемерия, строительства городов,
технических и военных сооружений.
13.
Огромный вклад в развитие прикладнойгеометрии внёс трактат « Математика
морского острова», в котором приведены
решения различных задач на определение
расстояний до предметов, расположенных
на отдалённом расстоянии, и вычисление
недоступных высот и расстояний.
14.
15.
16.
17.
18.
19.
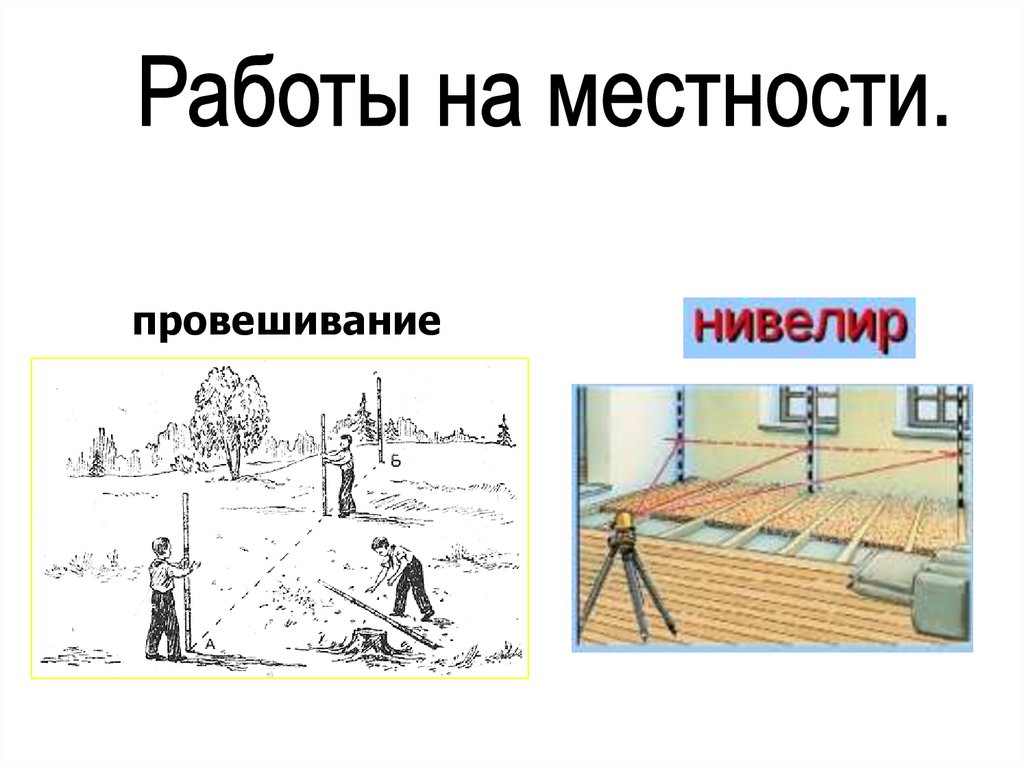
провешивание20.
21.
22.
Ответить на вопросы:23.
24.
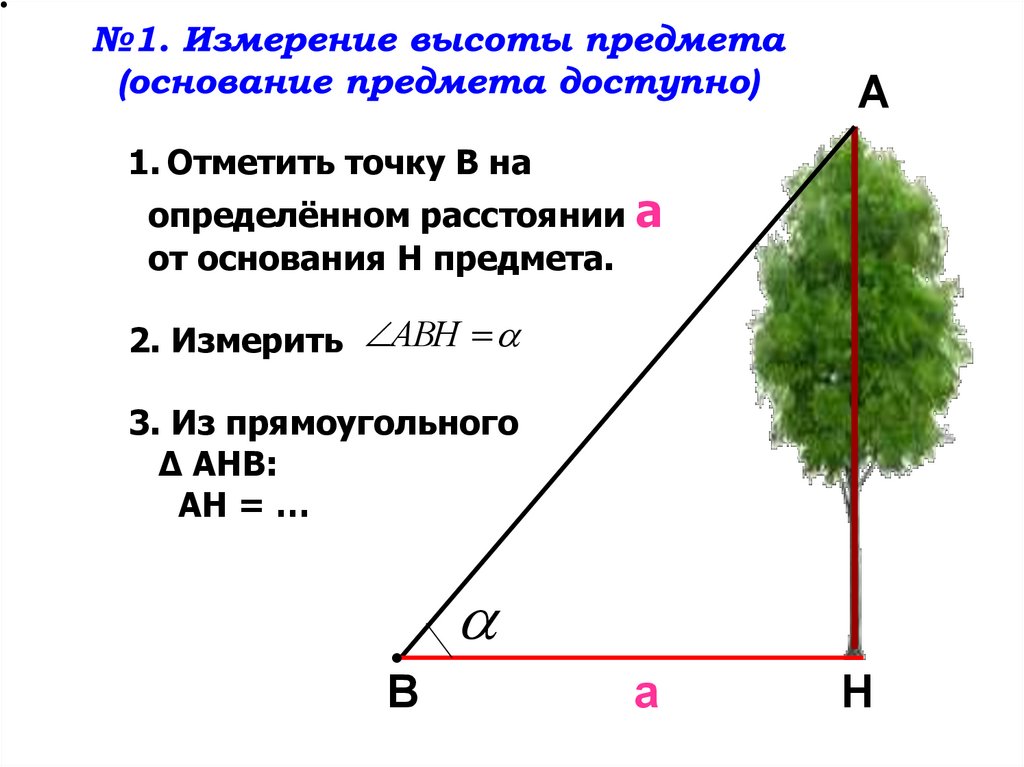
А1. Отметить точку В на
определённом расстоянии
от основания H предмета.
а
2. Измерить АВН
3. Из прямоугольного
∆ АHВ:
АH = …
В
а
Н
25.
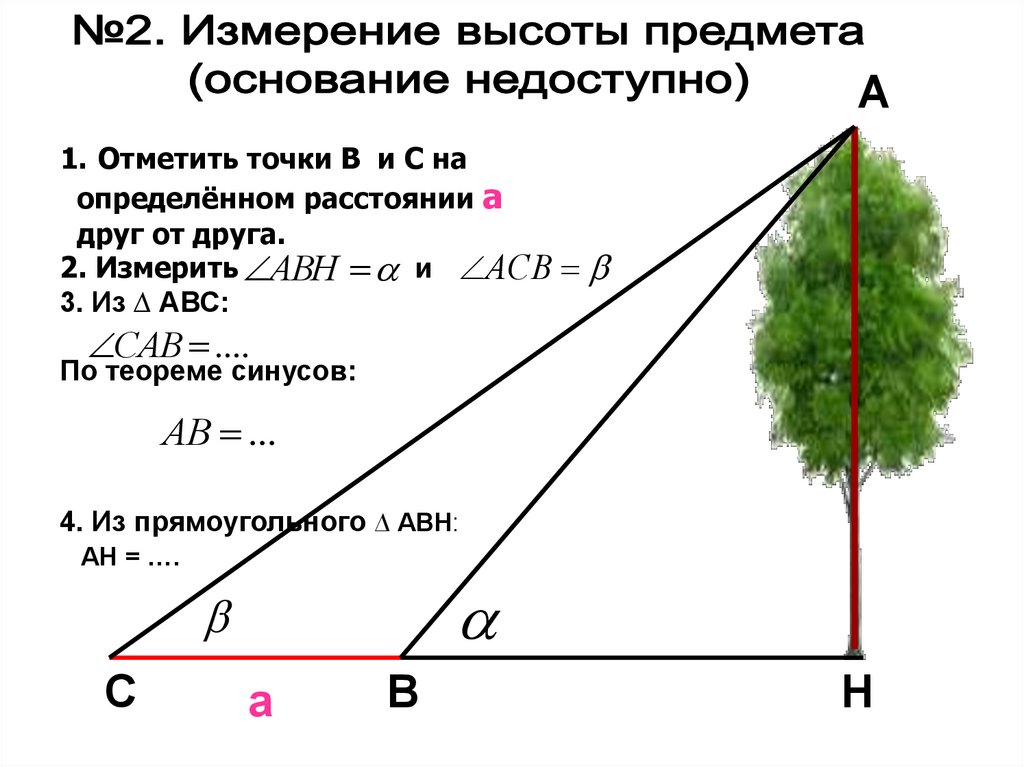
А26.
А1. Отметить точки В и С на
определённом расстоянии а
друг от друга.
2. Измерить АВН и АСВ
3. Из ∆ АВС:
САВ ....
По теореме синусов:
АВ ...
4. Из прямоугольного ∆ АВH:
АH = ….
С
а
В
Н
27.
28.
29.
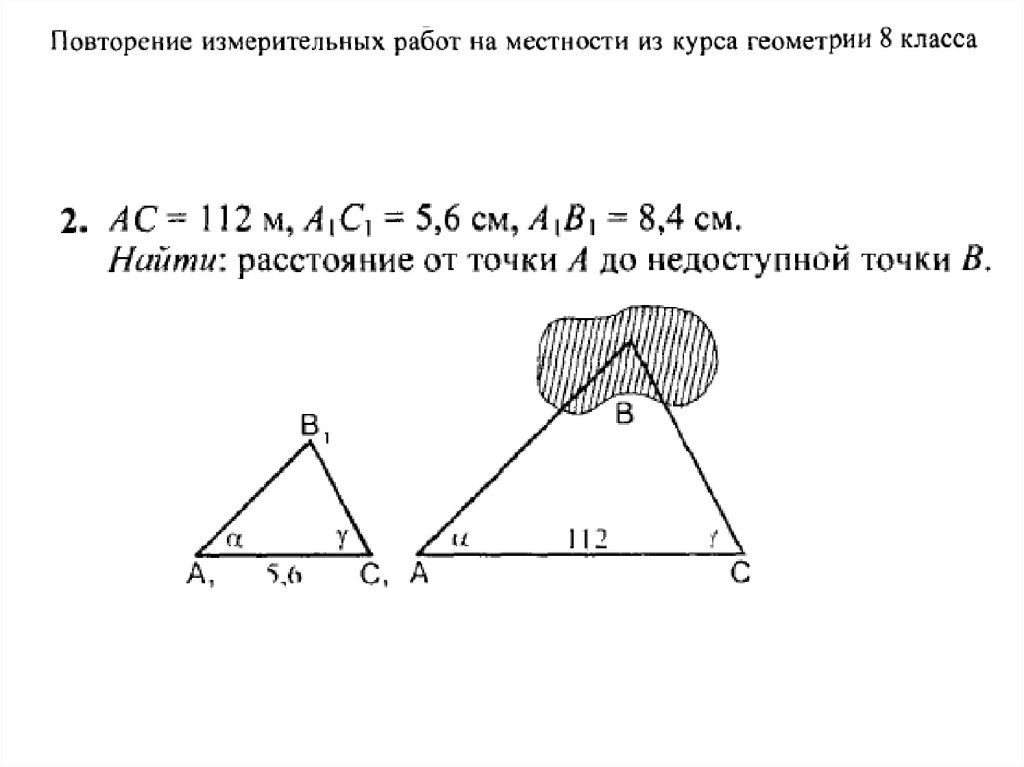
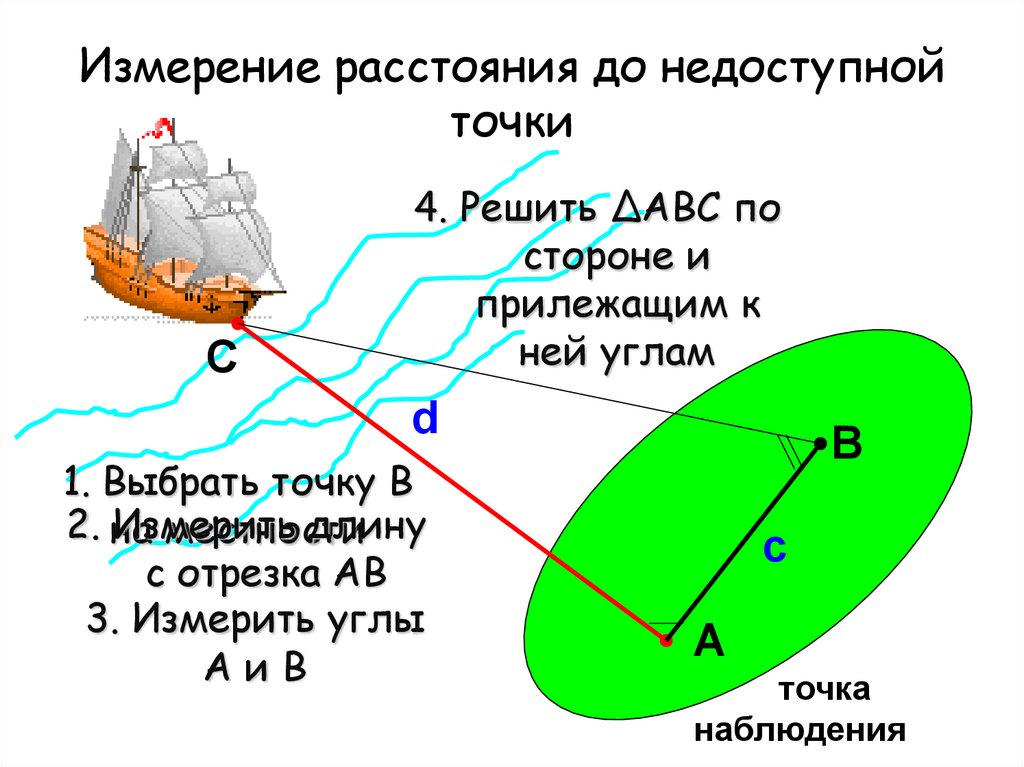
Измерение расстояния до недоступнойточки
C
4. Решить ∆АВС по
стороне и
прилежащим к
ней углам
d
1. Выбрать точку В
2. на
Измерить
длину
местности
с отрезка АВ
3. Измерить углы
АиВ
B
c
A
точка
наблюдения














 mathematics
mathematics








