Prisma. Definiţii, notaţii

1. Diapozitivul 1

Definiţii, notaţii
Prisme particulare
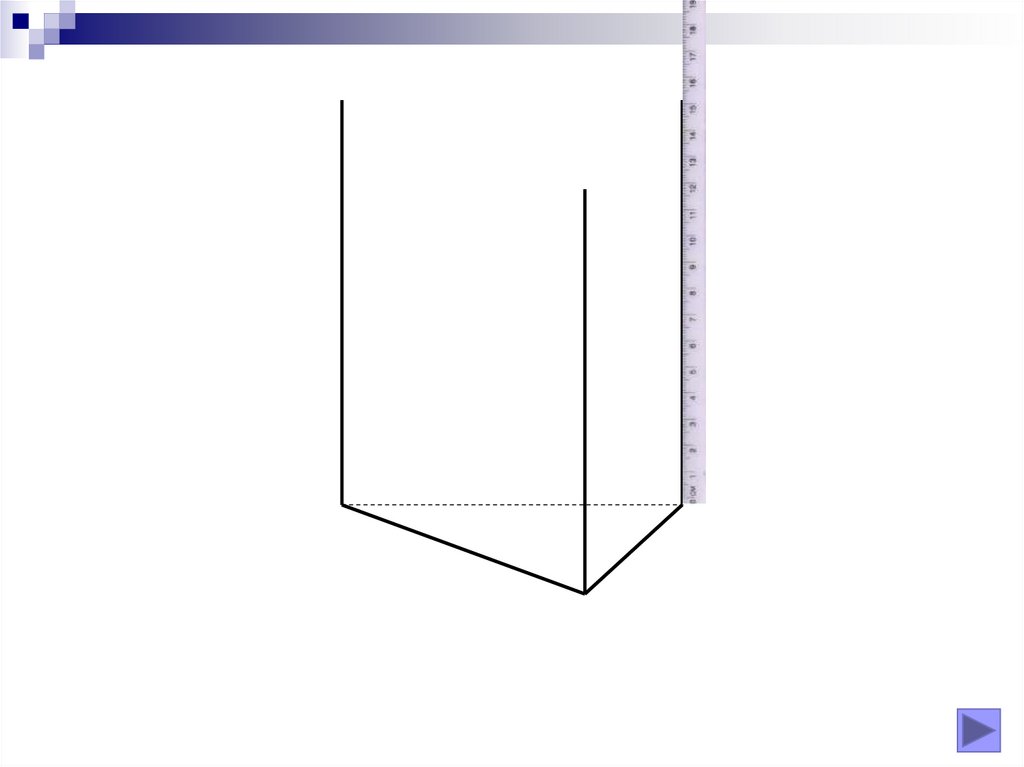
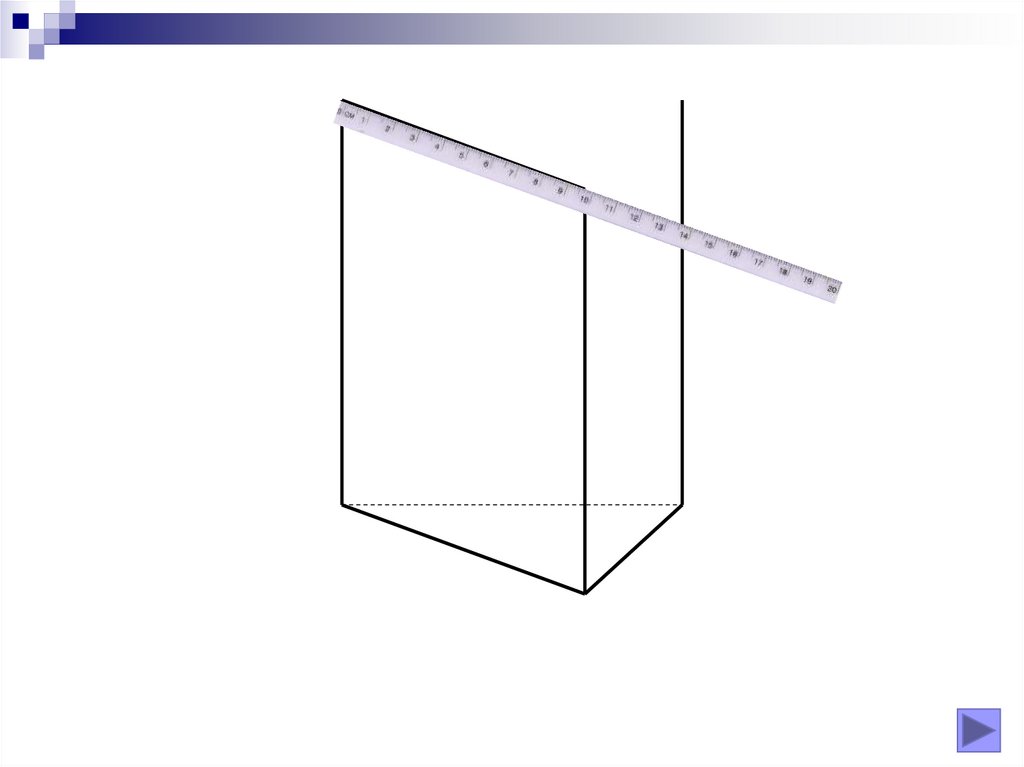
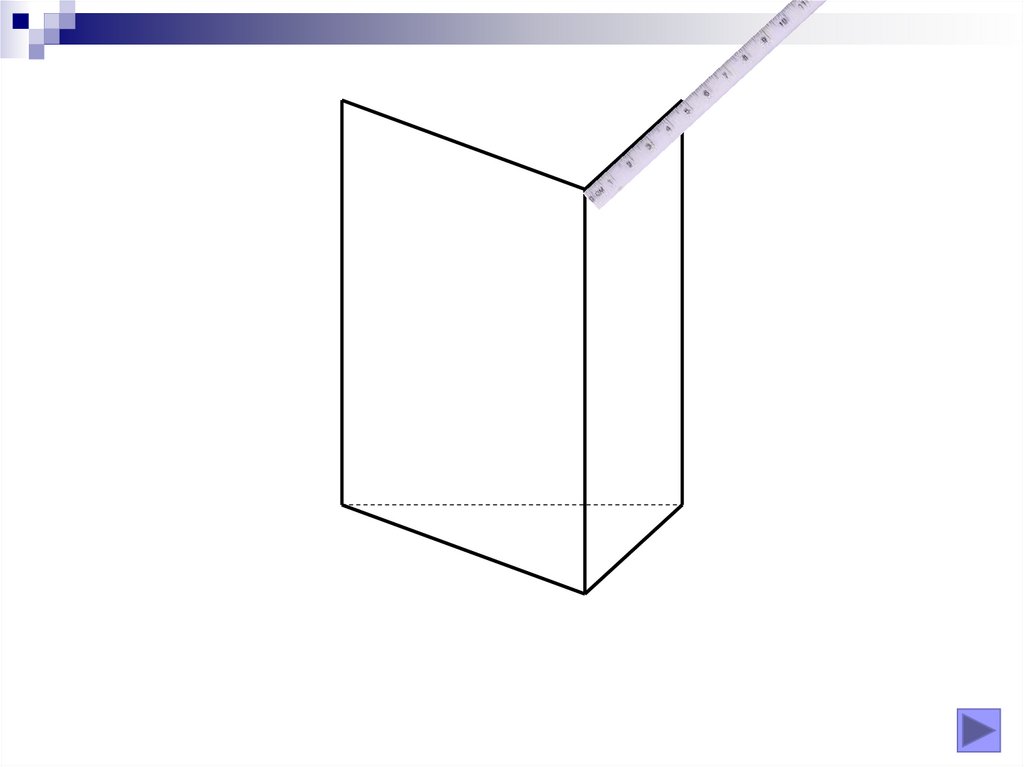
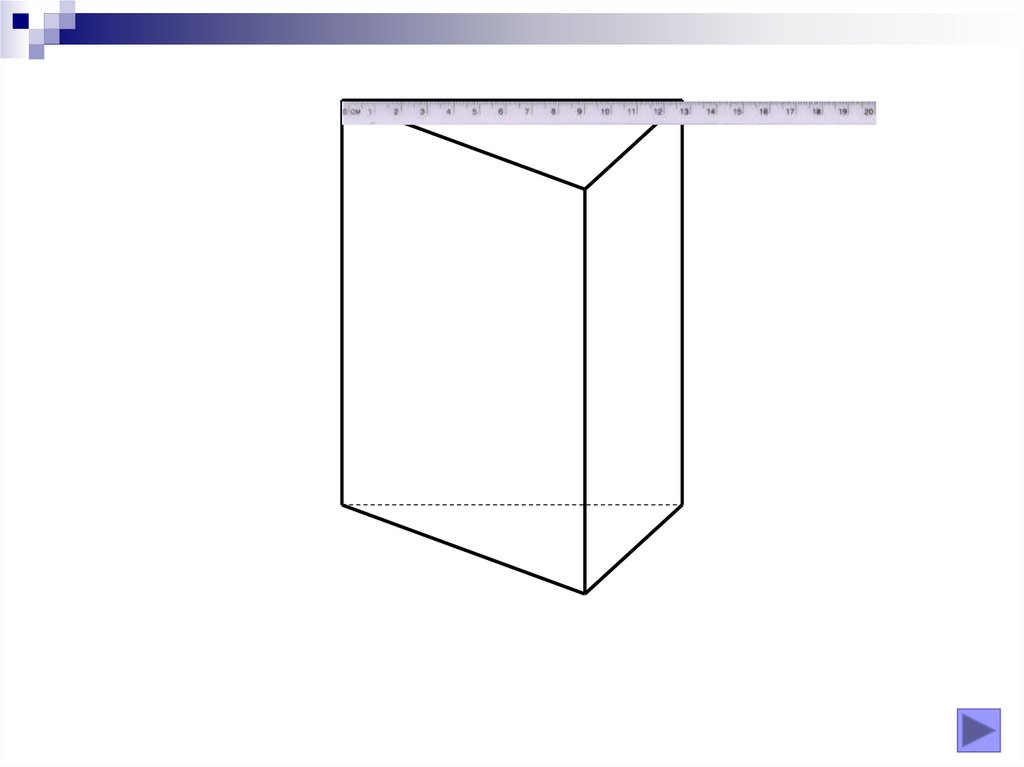
Realizarea desenelor
Formule de calcul
Probleme

2. Diapozitivul 2

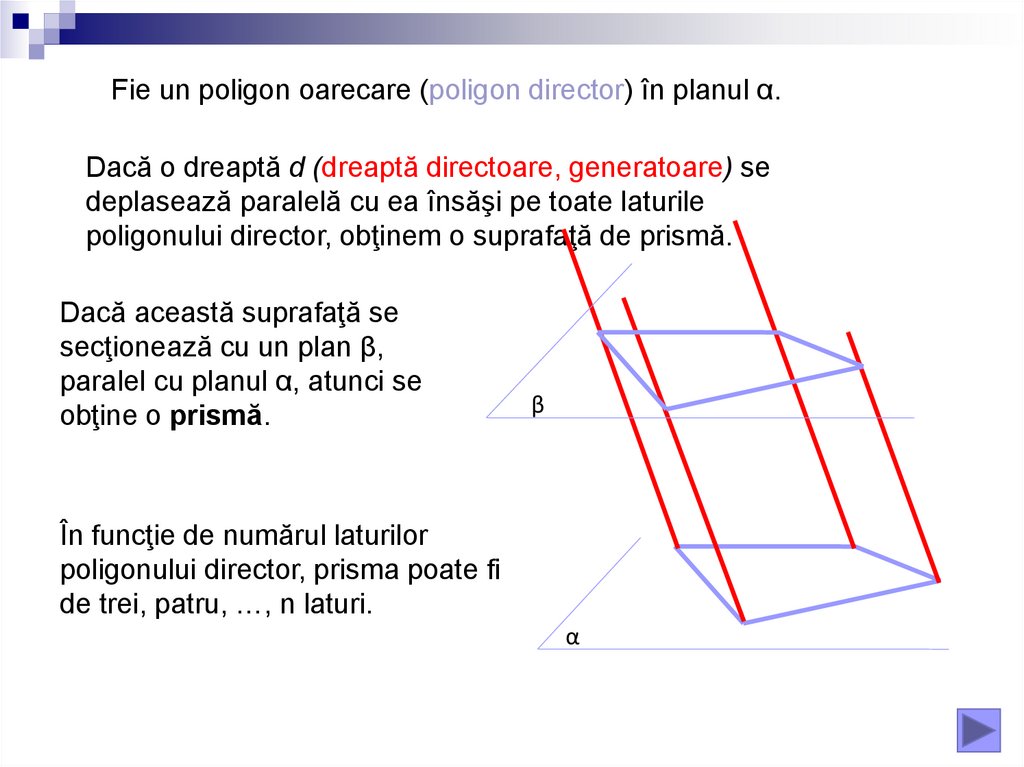
Fie un poligon oarecare (poligon director) în planul α.
Dacă o dreaptă d (dreaptă directoare, generatoare) se
deplasează paralelă cu ea însăşi pe toate laturile
poligonului director, obţinem o suprafaţă de prismă.
Dacă această suprafaţă se
secţionează cu un plan β,
paralel cu planul α, atunci se
obţine o prismă.
β
În funcţie de numărul laturilor
poligonului director, prisma poate fi
de trei, patru, …, n laturi.
α

3. Diapozitivul 3

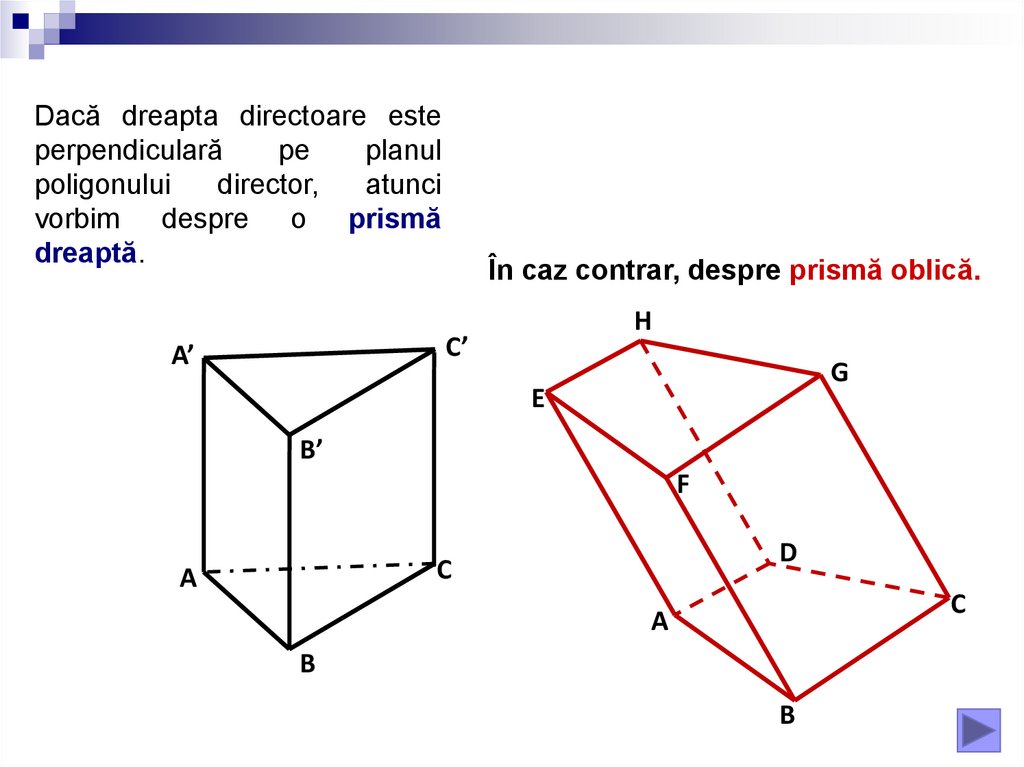
Dacă dreapta directoare este
perpendiculară
pe
planul
poligonului
director,
atunci
vorbim despre o prismă
dreaptă.
În caz contrar, despre prismă oblică.
H
C’
A’
G
E
B’
F
D
C
A
C
A
B
B

4. Diapozitivul 4

C’
D’
A’
B’
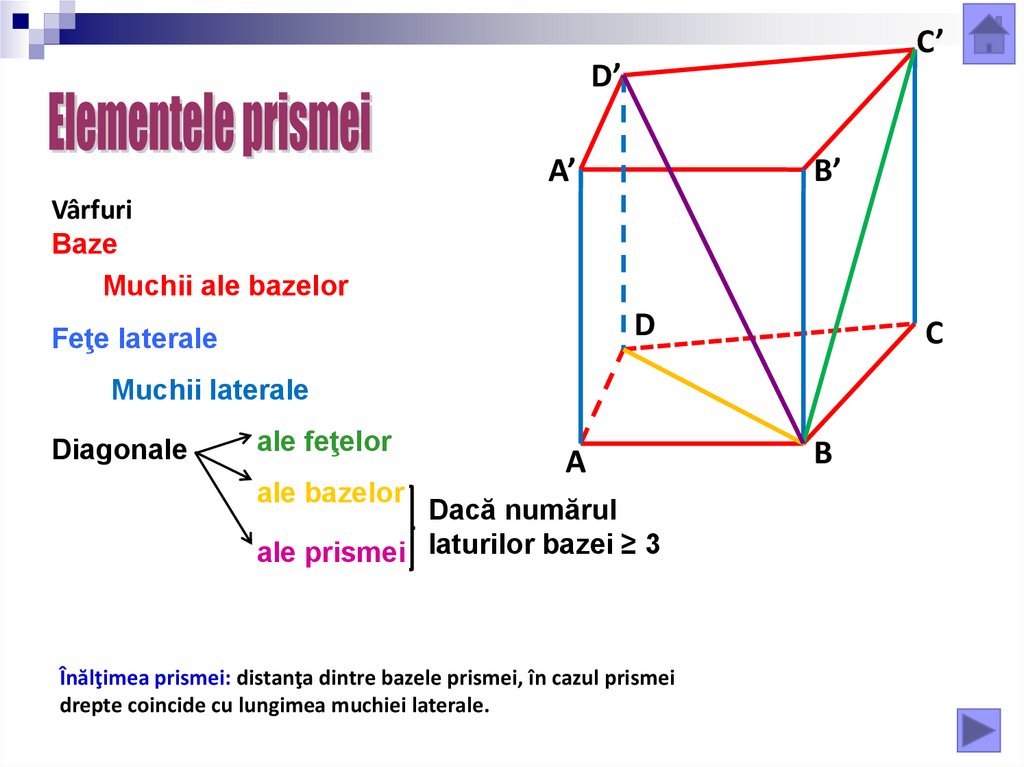
Vârfuri
Baze
Muchii ale bazelor
D
Feţe laterale
C
Muchii laterale
Diagonale
ale feţelor
A
ale bazelor
Dacă numărul
ale prismei laturilor bazei ≥ 3
Înălţimea prismei: distanţa dintre bazele prismei, în cazul prismei
drepte coincide cu lungimea muchiei laterale.
B

5. Diapozitivul 5

Dacă baza prismei este un poligon regulat ( triunghi echilateral,
pătrat, hexagon regulat, etc) atunci prisma se numeşte prismă
regulată.
Feţele laterale ale prismei regulate sunt dreptunghiuri congruente.
! !Dacă baza prismei drepte este un dreptunghi, atunci prisma NU
este regulată! !
Dacă toate feţele prismei sunt paralelograme, atunci se
numeşte paralelipiped.
Dacă toate feţele sunt dreptunghiuri, atunci este un
paralelipiped dreptunghic.
paralelipiped dreptunghic = paralelipiped drept
Dacă toate muchiile prismei sunt congruente (toate feţele
pătrate), atunci vorbim despre un cub.

6. Diapozitivul 6

Paralelipiped dreptunghic
Cub
Prismă triunghiulară (regulată) dreaptă
Prismă hexagonală regulată dreaptă

7. Diapozitivul 7

Paralelipiped dreptunghic
Cub

8. Diapozitivul 8

9. Diapozitivul 9

10. Diapozitivul 10

11. Diapozitivul 11

12. Diapozitivul 12

13. Diapozitivul 13

14. Diapozitivul 14

15. Diapozitivul 15

16. Diapozitivul 16

17. Diapozitivul 17

18. Diapozitivul 18

19. Diapozitivul 19

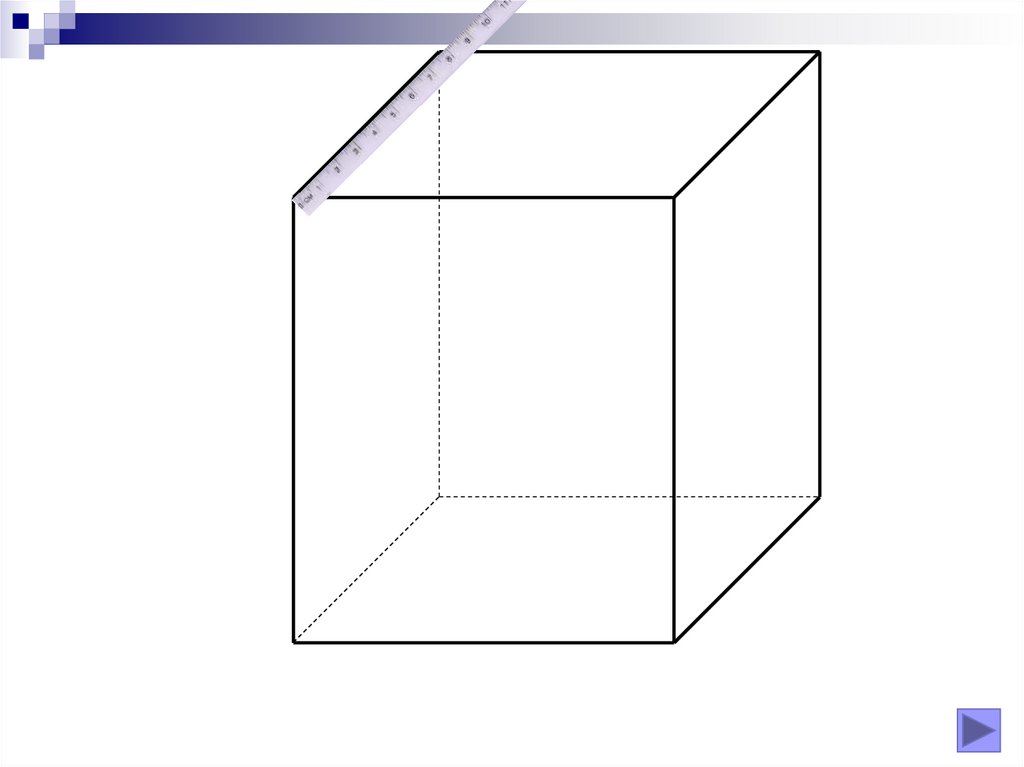
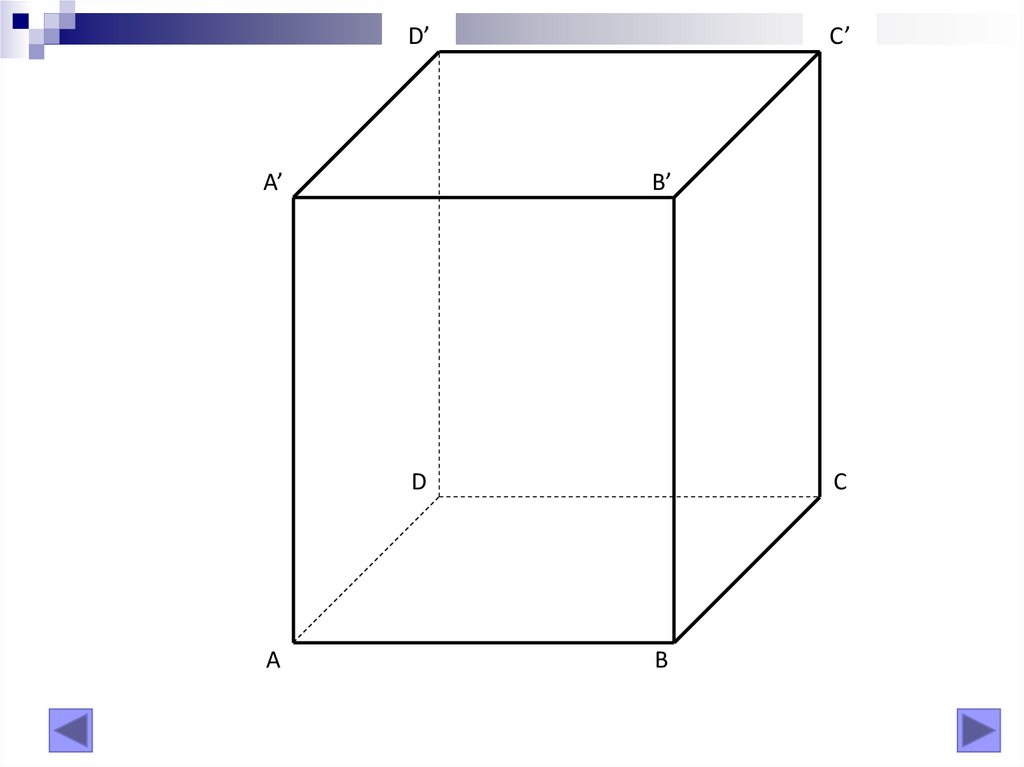
D’
A’
C’
B’
D
A
C
B

20. Diapozitivul 20

21. Diapozitivul 21

22. Diapozitivul 22

23. Diapozitivul 23

24. Diapozitivul 24

25. Diapozitivul 25

26. Diapozitivul 26

27. Diapozitivul 27

28. Diapozitivul 28

29. Diapozitivul 29

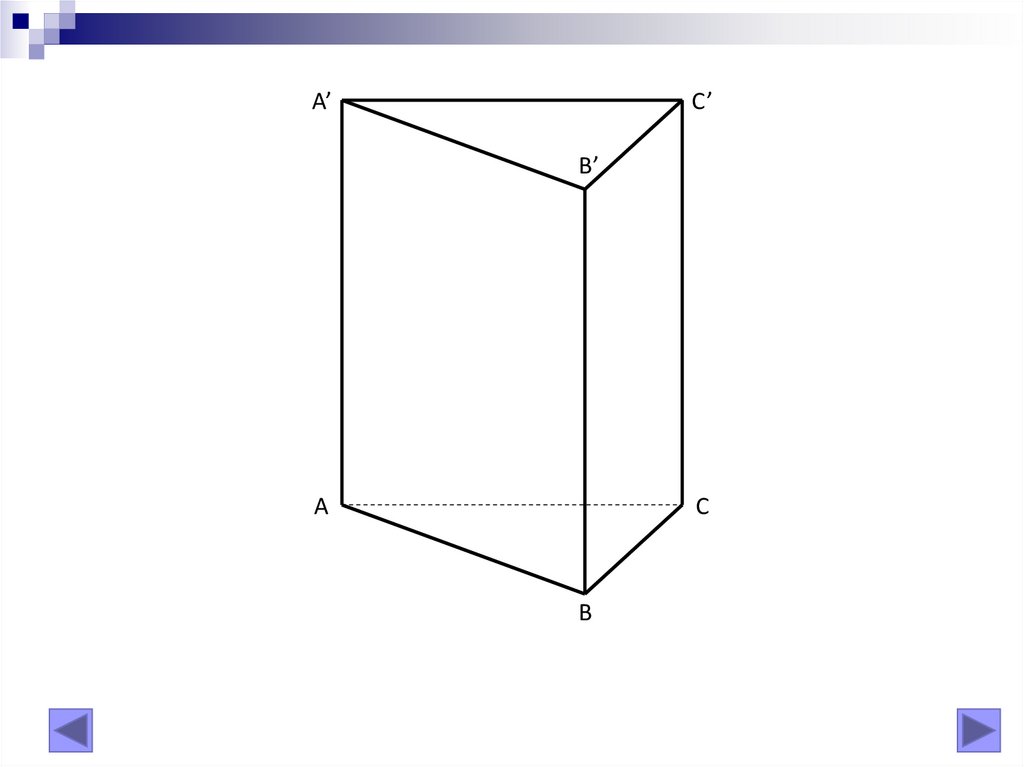
A’
C’
B’
A
C
B

30. Diapozitivul 30

31. Diapozitivul 31

32. Diapozitivul 32

33. Diapozitivul 33

34. Diapozitivul 34

35. Diapozitivul 35

36. Diapozitivul 36

37. Diapozitivul 37

38. Diapozitivul 38

39. Diapozitivul 39

40. Diapozitivul 40

41. Diapozitivul 41

42. Diapozitivul 42

43. Diapozitivul 43

44. Diapozitivul 44

45. Diapozitivul 45

46. Diapozitivul 46

47. Diapozitivul 47

48. Diapozitivul 48

E’
D’
C’
F’
A’
B’
E
D
C
F
A
B

49. Diapozitivul 49

Al= arie laterală=suma ariilor feţelor
laterale
At= arie totală = Al + ariile bazelor
At = Al + 2Abază
V = volum= Abază . înălţime

50. Diapozitivul 50

Formule particulare
Al = Pbază· înălţime
Paralelipiped
dreptunghic:
Cub:
(pentru orice prismă dreaptă)
Al = 2ac+2bc
At = 2ab+2ac+2bc
V= abc
d2 = a2+b2+c2
Al= 4a2
At = 6a2
V = a3
d2 = 3a2
a =muchia cubului
a= lungime
b = lăţime
c =înălţime
d =diagonala prismei

51. Diapozitivul 51

Probleme ce se rezolvă (şi) fără desen
Probleme a căror rezolvare necesită desen
Probleme propuse

52. Diapozitivul 52

1. Dimensiunile unui paralelipiped dreptunghic sunt de
7cm, 4cm, 8cm. Calculaţi aria laterală şi volumul.
R1
2. Volumul unui cub este de 125 cm3. Calculaţi aria
totală a cubului.
R2
3. O prismă triunghiulară regulată are muchia bazei de 4cm,
înălţimea de 8 cm. Determinaţi aria laterală şi volumul ei.
R3
4. Suma dimensiunilor unui paralelipiped dreptunghic
este de 24 cm, lungimea diagonalei de 18 cm. Calculaţi
aria totală a paralelipipedului.
R4
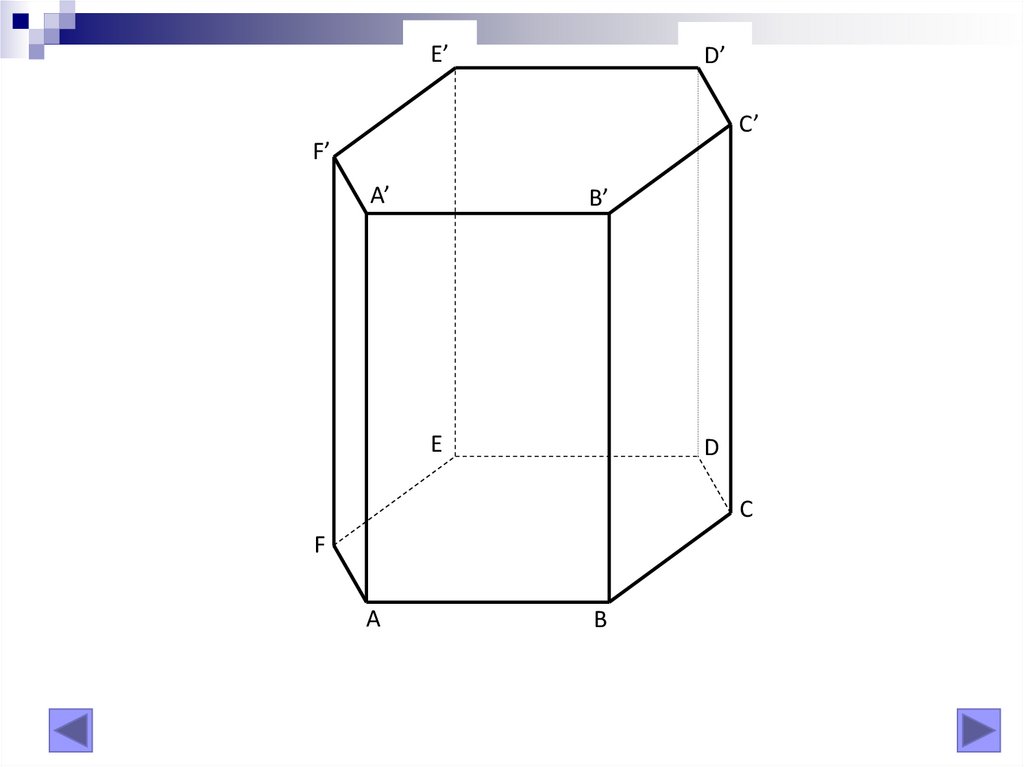
5. O prismă hexagonală regulată are muchia bazei de 2cm,
iar feţele laterale sunt pătrate. Calculaţi aria laterală şi
volumul prismei.
R5
Probleme

53. Diapozitivul 53

R1
Avem a 7cm, b 8cm, c 4cm
Al 2ac 2bc
V abc
Deci:
Al 2 7 8 4 2 15 4 120 cm
V 7 8 4 224 cm3
2

54. Diapozitivul 54

R2
Avem V 125cm
3
V a 125 a 5 a a 5cm
3
deci
At 6 a 2
3
3
3
At 6 52 6 25 150 cm 2

55. Diapozitivul 55

R3
Prisma este regulată, deci are ca bază un triunghi echilateral
Fie a=4 cm lungimea laturii bazei, h=8 cm înălţimea prismei.
Al Pbaza h
Al 3 4 8 96 cm 2
V Abaza h
a2 3
Abaza
4
Abaza
V 4 3 8 32 3 cm3
16 3
4 3 cm 2
4

56. Diapozitivul 56

R5
Deoarece feţele prismei sunt pătrate, înălţimea
corespunde cu muchia bazei: a=h=2 cm.
Al Pbaza h
V Abaza h
Al 6 2 2 24 cm 2
a2 3
V 6
h
4
4 3
V 6
2 12 3 cm3
4

57. Diapozitivul 57

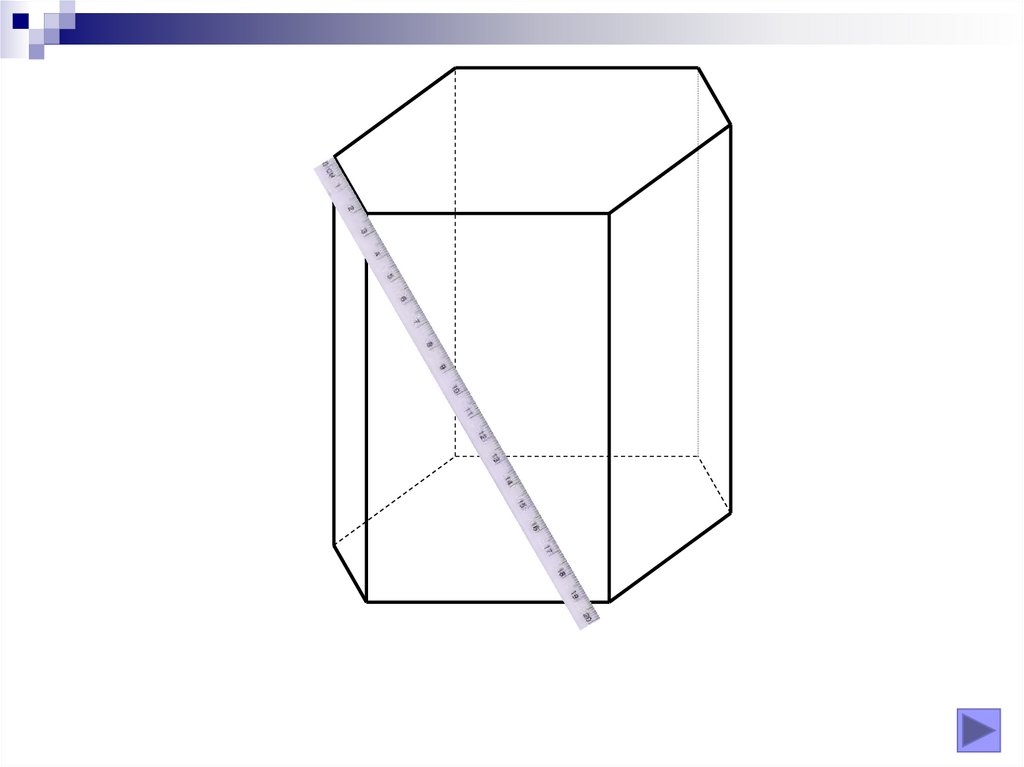
1. Fie ABCDA’B’C’D’ un cub.Fie M mijlocul lui A’D’, iar P mijlocul lui AB. Dacă
3
MP=
cm,4 calculaţi
muchia şi volumul cubului.
R1
2. Fie ABCDEF o prismă dreaptă, având baza ABC triunghi dreptunghic.
Înălţimea prismei este congruentă cu ipotenuza bazei, ([AD]≡[AC]) şi
AB=12cm, BC=9cm. Calculaţi:
a) Aria totală şi volumul prismei;
b) Aria triunghiului EBM, unde M este mijlocul AC.
R2
3. Fie ABCDA’B’C’D’ o prismă patrulateră regulată cu muchia bazei AB=2 cm.
Dacă aria triunghiului A’BC este de 4 cm2, calculaţi:
a) Volumul prismei,
b) sinusul unghiului format de diagonala prismei cu planul bazei.
R3
4. Fie ABCA’B’C’ o prismă triunghulară regulată. Se ştie că distanţa dintre
centrele a două feţe laterale este de 4 cm, şi aria laterală de 96 3cm2.
Calculaţi:
a) Înălţimea prismei
b) Volumul prismei
c) Măsura unghiului format de planele (A’BC) şi (ABC).
Probleme
R4

58. Diapozitivul 58

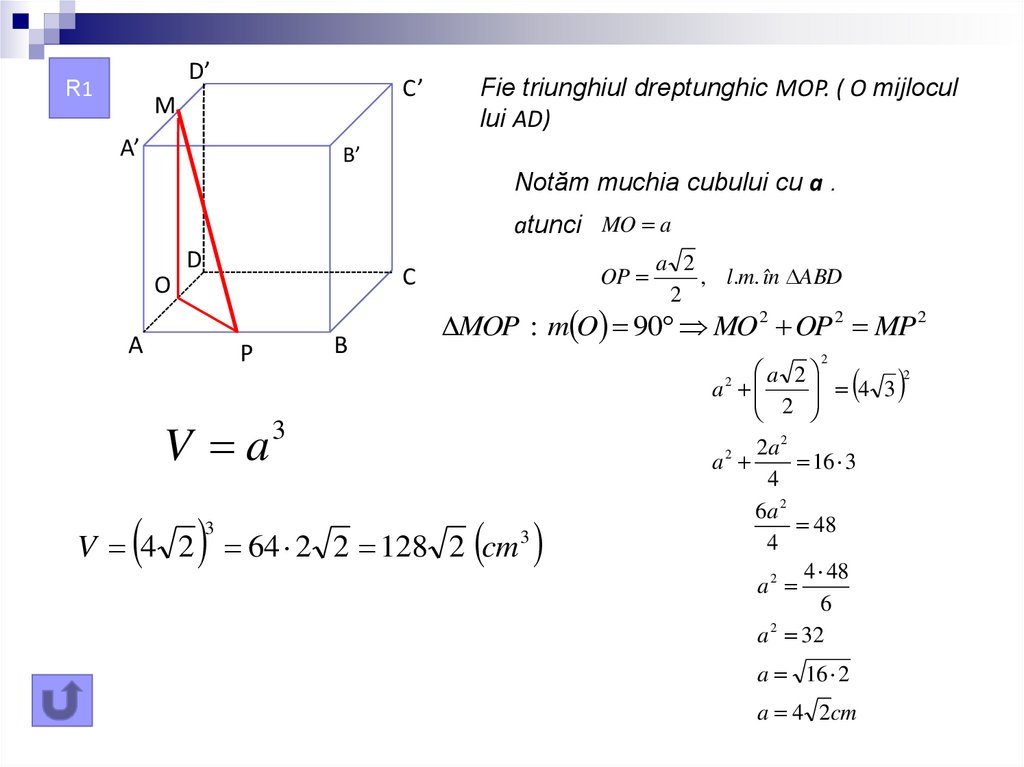
D’
R1
C’
M
A’
B’
Fie triunghiul dreptunghic MOP. ( O mijlocul
lui AD)
Notăm muchia cubului cu a .
atunci MO a
O
D
OP
C
A
P
B
MOP : m O 90 MO 2 OP 2 MP 2
2
V a3
3
a 2
, l.m. în ABD
2
V 4 2 64 2 2 128 2 cm3
a 2
4 3
a 2
2
2a 2
2
a
16 3
4
6a 2
48
4
4 48
a2
6
a 2 32
a 16 2
a 4 2cm
2

59. Diapozitivul 59

R4
avem a b c 24
d 18 d 2 324 a 2 b 2 c 2 324
dar
a b c 2 a 2 b 2 c 2 2ab 2ac 2bc
At
deci
24 324 At
2
576 324 At
At 576 324 252 cm 2

60. Diapozitivul 60

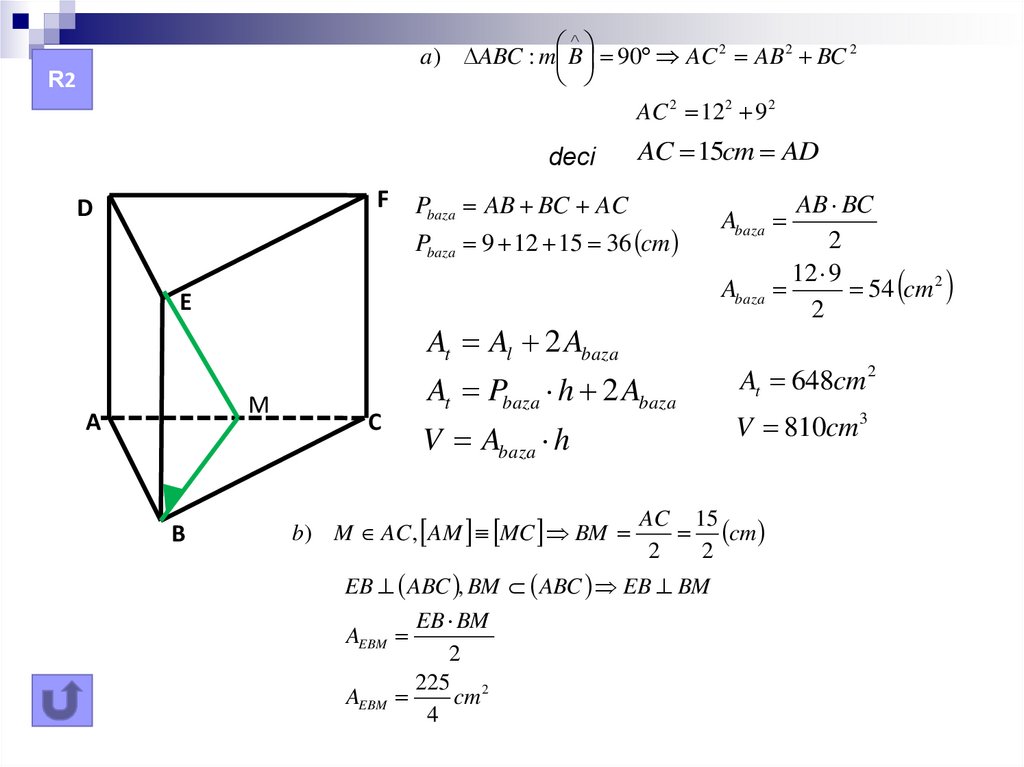
a) ABC : m B 90 AC 2 AB 2 BC 2
AC 2 12 2 9 2
R2
deci
F
D
AC 15cm AD
Pbaza AB BC AC
Pbaza 9 12 15 36 cm
E
At Al 2 Abaza
M
A
B
At Pbaza h 2 Abaza
C
V Abaza h
b) M AC , AM MC BM
EB BM
2
225 2
cm
4
AEBM
At 648cm 2
V 810cm3
AC 15
cm
2
2
EB ABC , BM ABC EB BM
AEBM
AB BC
2
12 9
Abaza
54 cm 2
2
Abaza

61. Diapozitivul 61

D’
C’
a) Ce fel de triunghi este triunghiul A’BC?
R3
A’
B’
A' A ABC t 3
A' B BC m( A' BC ) 90
AB BC
AA'BC
D
C
A' B BC
A' B 2
4
A' B 4cm
2
2
A
B
A' AB : m( A) 90 A' A2 AB 2 A' B 2
A' A2 4 16 A' A 2 3cm m
V Abaza h V 22 2 3 8 3 cm3
b)
A' A ABC pr ABC A' C AC
sin A' C , ABC sin A' CA
A' AC : m( A) 90
A' A 2 3cm A' C 2 A' A2 AC 2
A' A 2 3
15
AC 2 2cm
A' C 2 5cm sin A' CA
A' C 2 5
5

62. Diapozitivul 62

B’
C’
R4
A’
a) Notăm cu O’ şi O centrele feţelor (A’ACC’)
şi (A’ABB’).
Deoarece diagonalele dreptunghiului se înjumătăţesc
OO’ este linie mijlocie în triunghiul A’CB.
O’
O
OO '
E
C
B
BC
BC 2OO ' BC 8cm
2
Al Pbaza h h
Al
Pbaza
h
96 3
4 3 cm
3 8
b) V Abaza h
A
c)
a 2 3 82 3
Abaza
16 3 cm 2
4
4
A' A ABC t 3
A' E BC
AE BC
m A 90
V 16 3 4 3 64 3 192 cm3
A' BC ABC BC
A' E BC
AE BC
A' AC :
m A' EA 45
a 3
A' A AE
4 3
2
A' BC , ABC A' EA