Piramida

1. Diapozitivul 1

Definiţii, notaţii
Piramide regulate
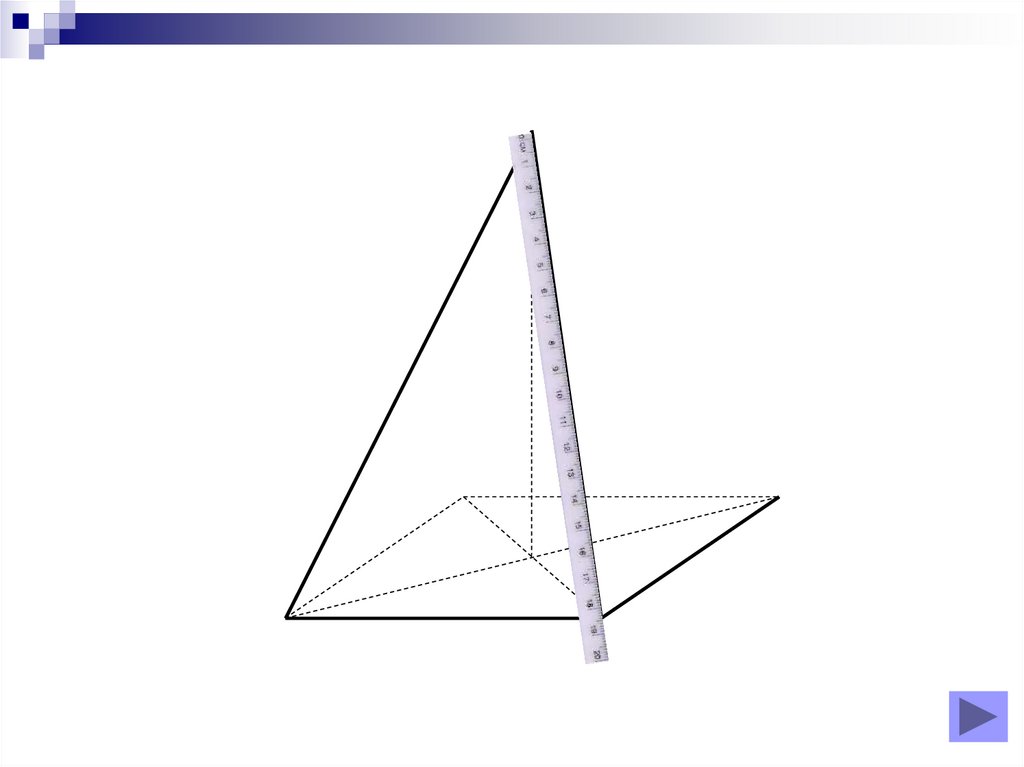
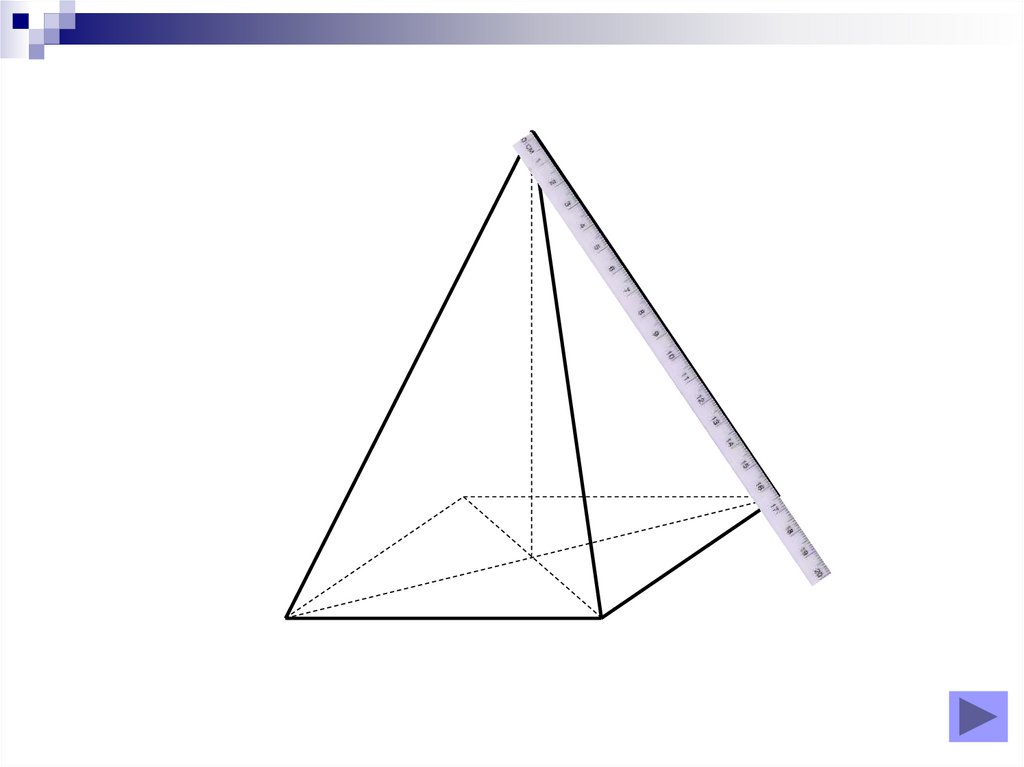
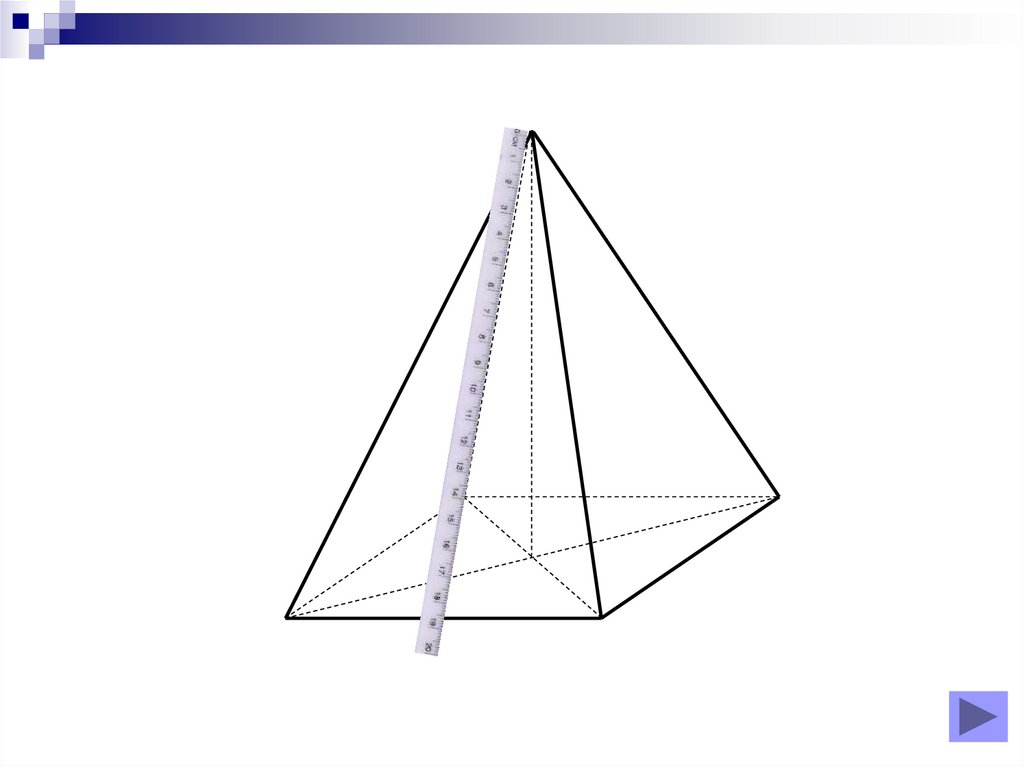
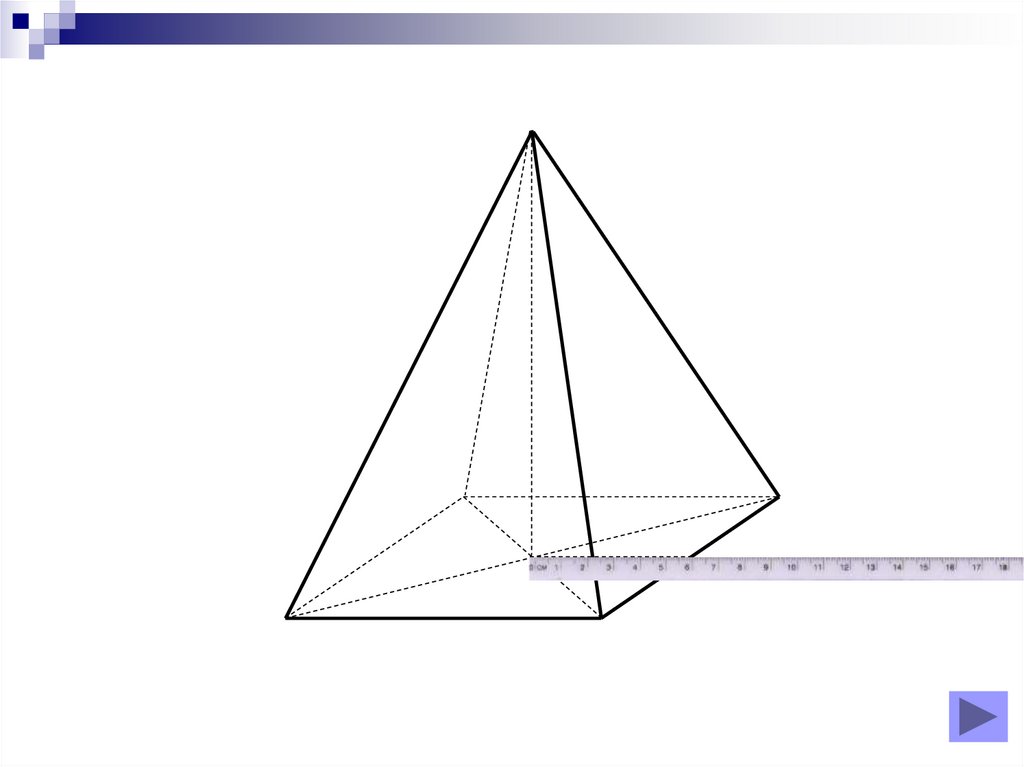
Realizarea desenelor
Formule de calcul
Aplicaţii

2. Diapozitivul 2

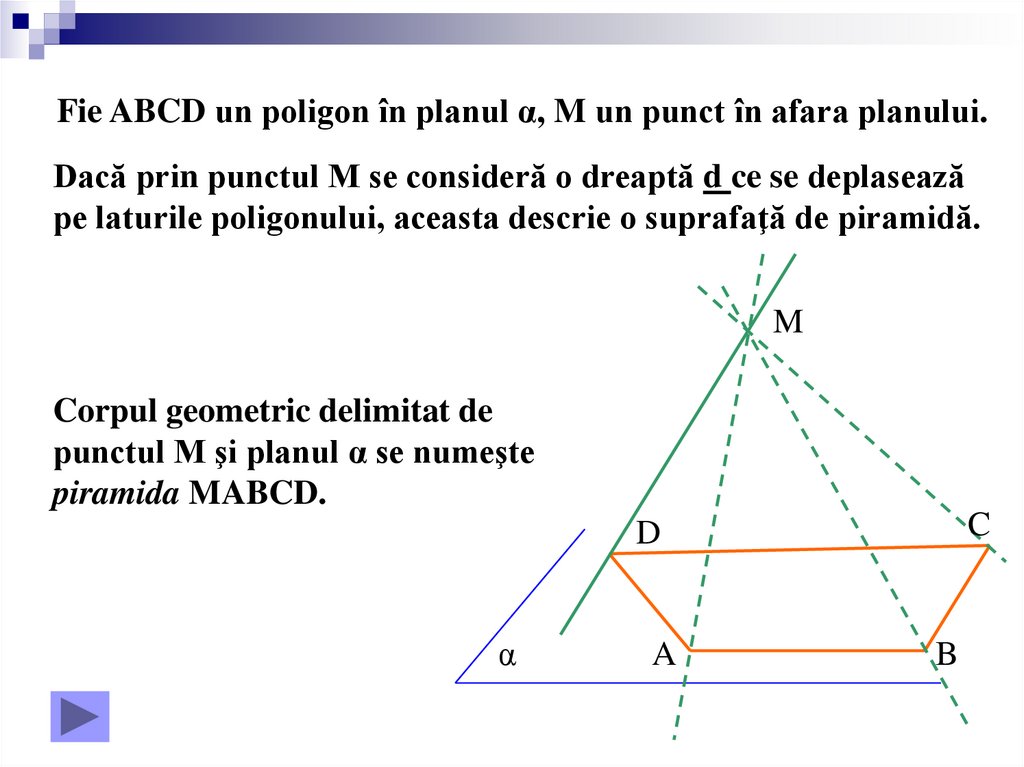
Fie ABCD un poligon în planul α, M un punct în afara planului.
Dacă prin punctul M se consideră o dreaptă d ce se deplasează
pe laturile poligonului, aceasta descrie o suprafaţă de piramidă.
M
Corpul geometric delimitat de
punctul M şi planul α se numeşte
piramida MABCD.
C
D
α
A
B

3. Diapozitivul 3

Elementele piramidei
V
Bază
Muchii ale bazei
Feţe laterale
Muchii laterale
Vârf
D
Înălţime: distanţa vârfului
piramidei de la planul bazei
C
A
B

4. Diapozitivul 4

S
S
A
O
S
O
C A
A
C
O
B
B
B
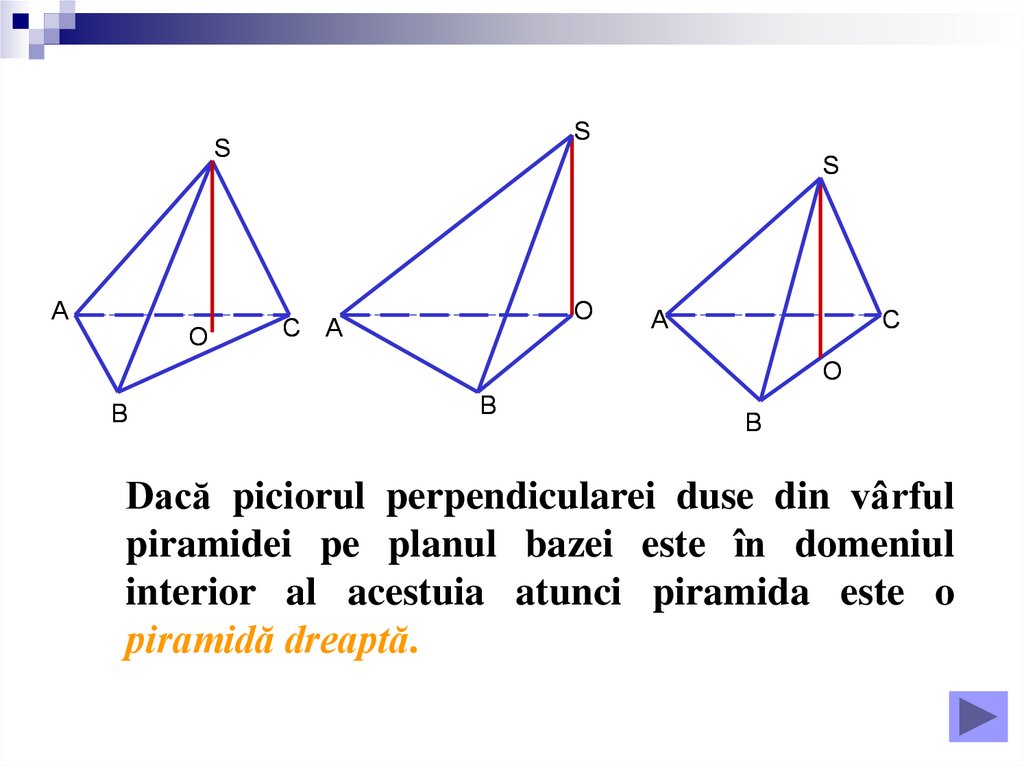
Dacă piciorul perpendicularei duse din vârful
piramidei pe planul bazei este în domeniul
interior al acestuia atunci piramida este o
piramidă dreaptă.

5. Diapozitivul 5

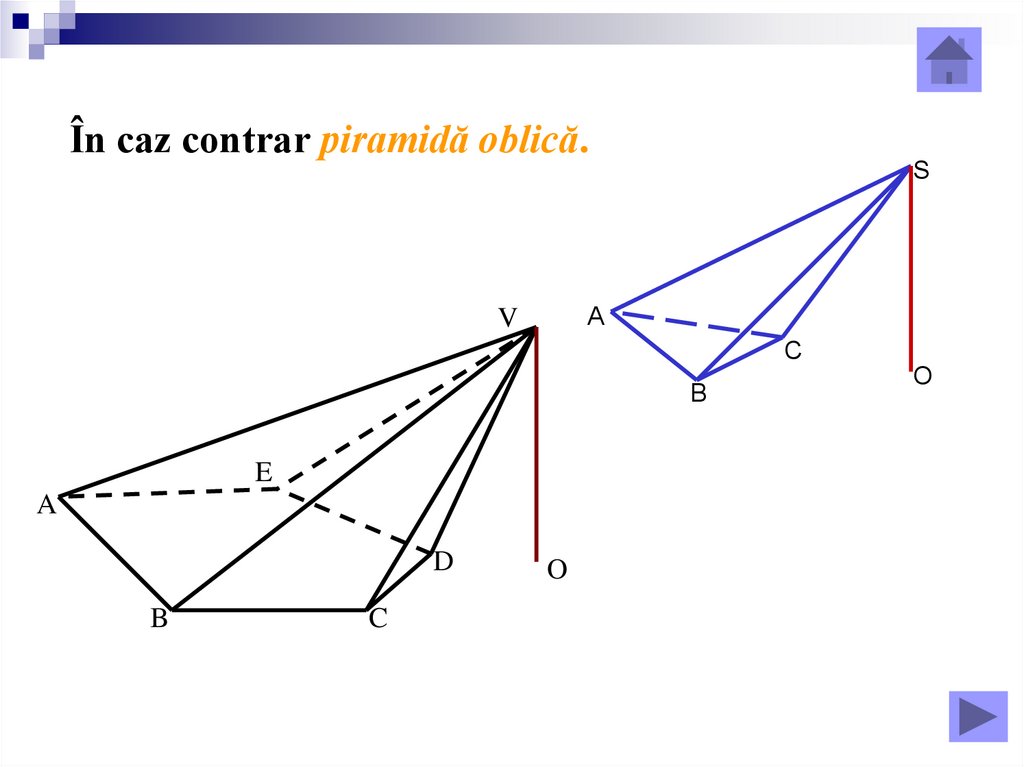
În caz contrar piramidă oblică.
S
A
V
C
B
E
A
D
B
C
O
O

6. Diapozitivul 6

Piramida regulată
O piramidă se numeşte regulată, dacă:
•Are ca bază un poligon regulat (∆ echilateral, pătrat,
hexagon regulat, etc)
•Piciorul perpendicularei duse din vârful piramidei
coincide cu centrul poligonului
•(centrul poligonului = centrul cercului circumscris).
Toate muchiile unei piramide regulate sunt congruente, deci
toate feţele sunt triunghiuri isoscele congruente.
Înălţimea unei feţe laterale se numeşte apotema piramidei.
Triunghiuri de lucru

7. Diapozitivul 7

Piramidă triunghiulară regulată
Piramidă patrulateră regulată
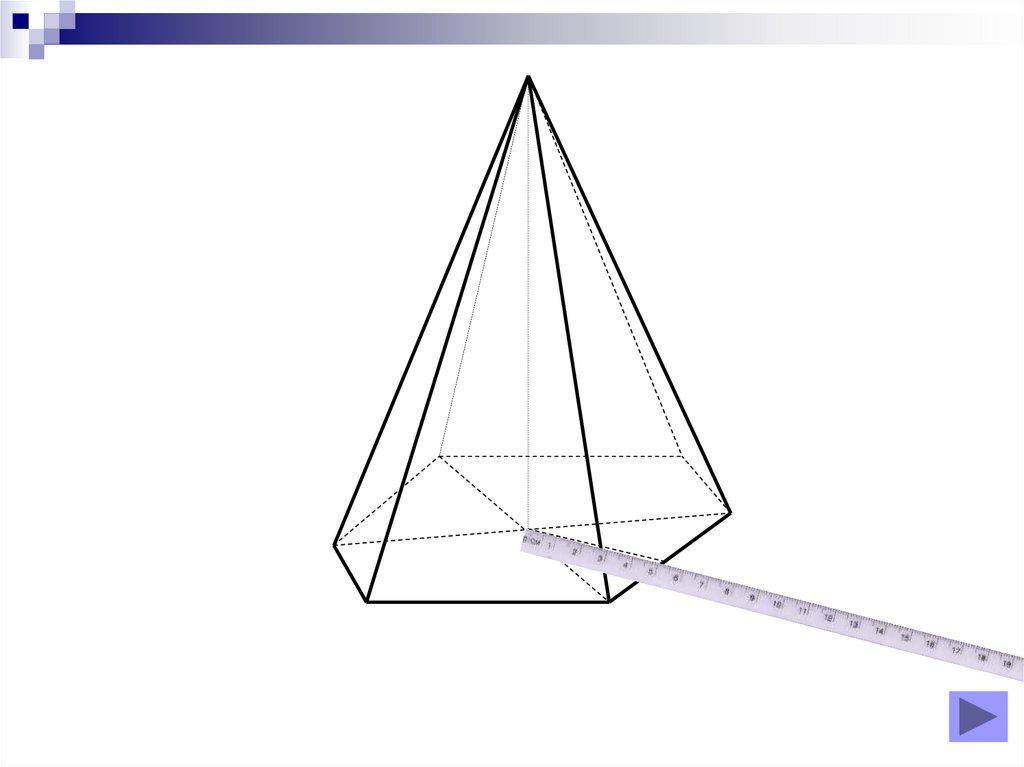
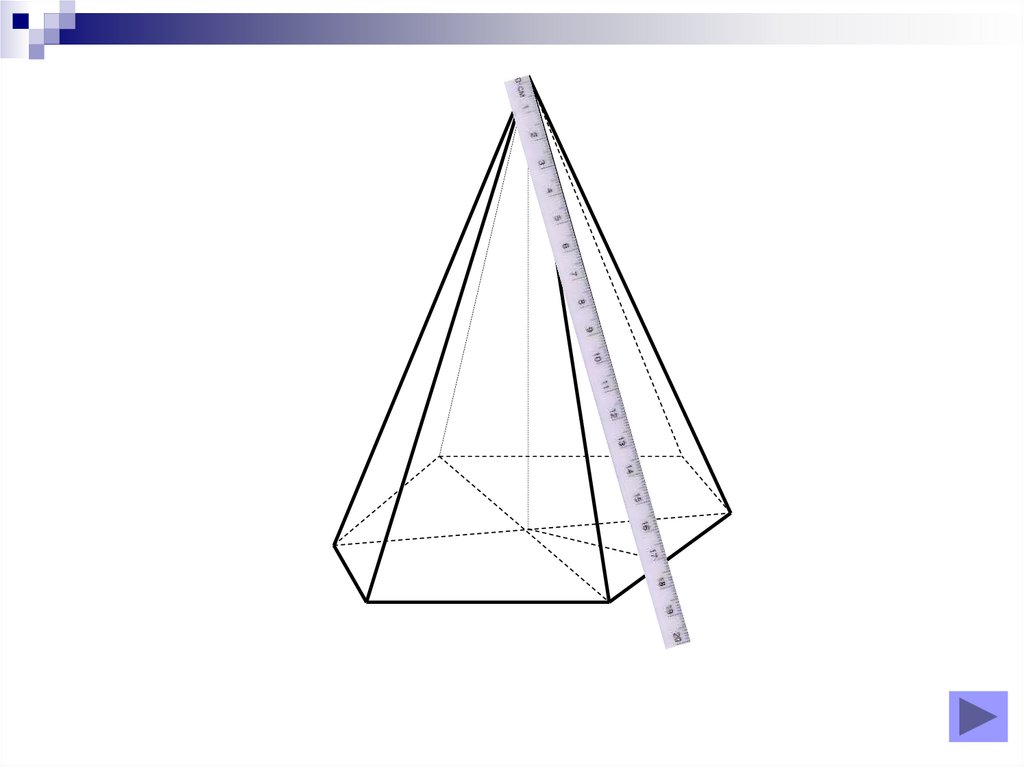
Piramidă hexagonală regulată

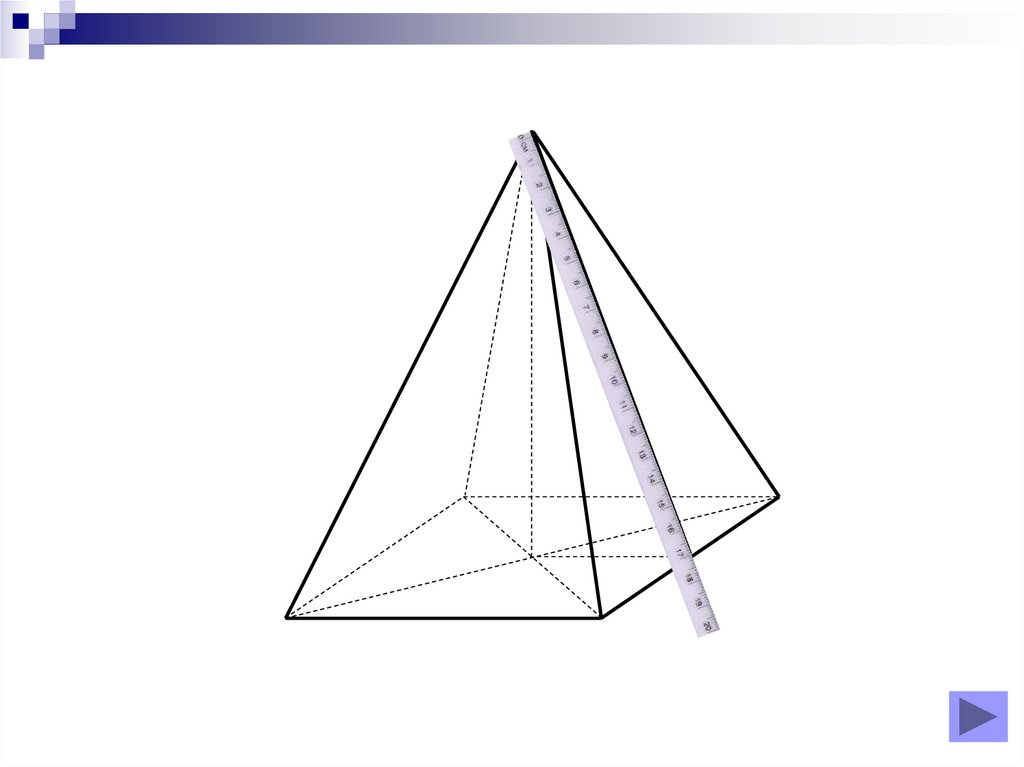
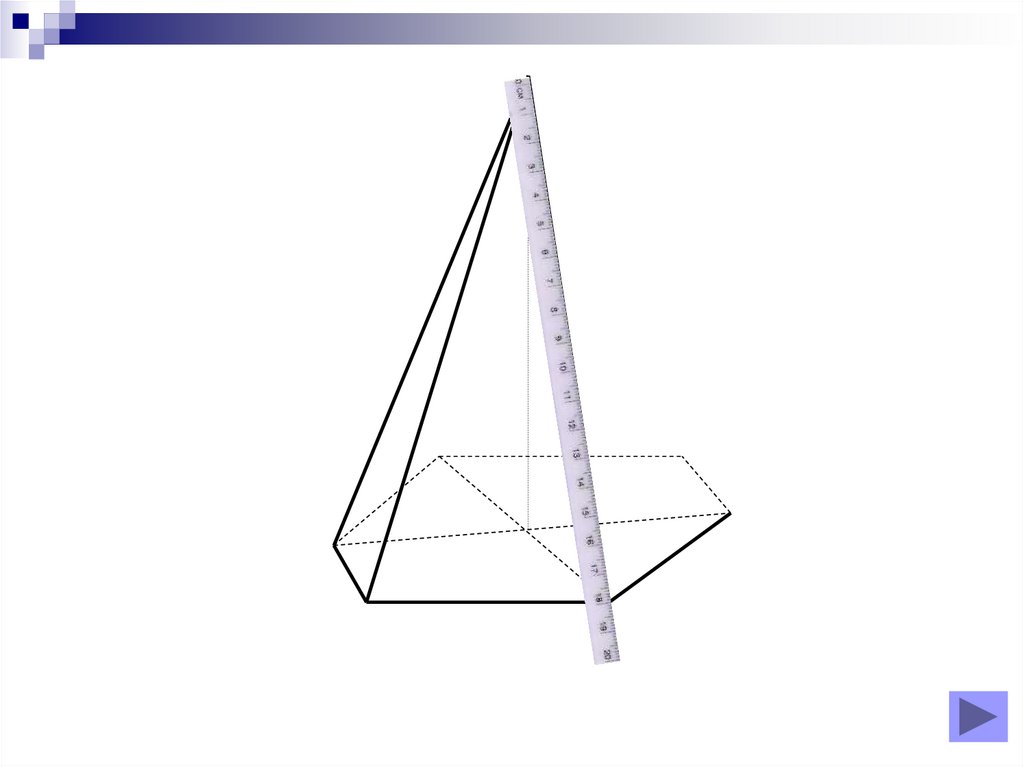
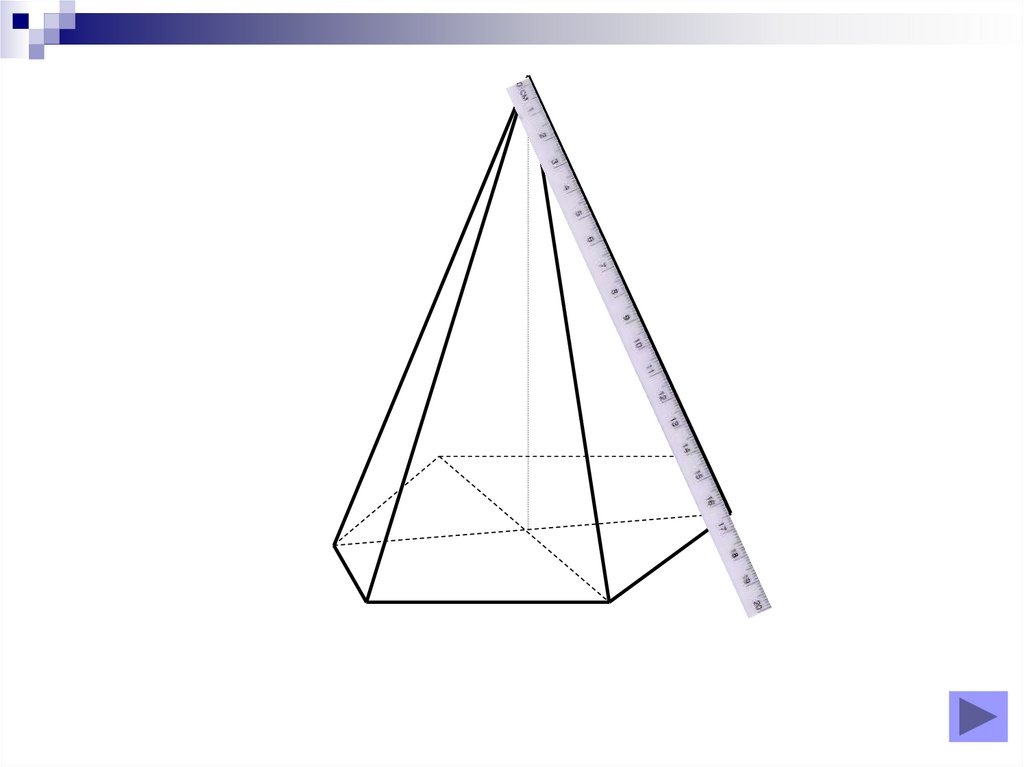
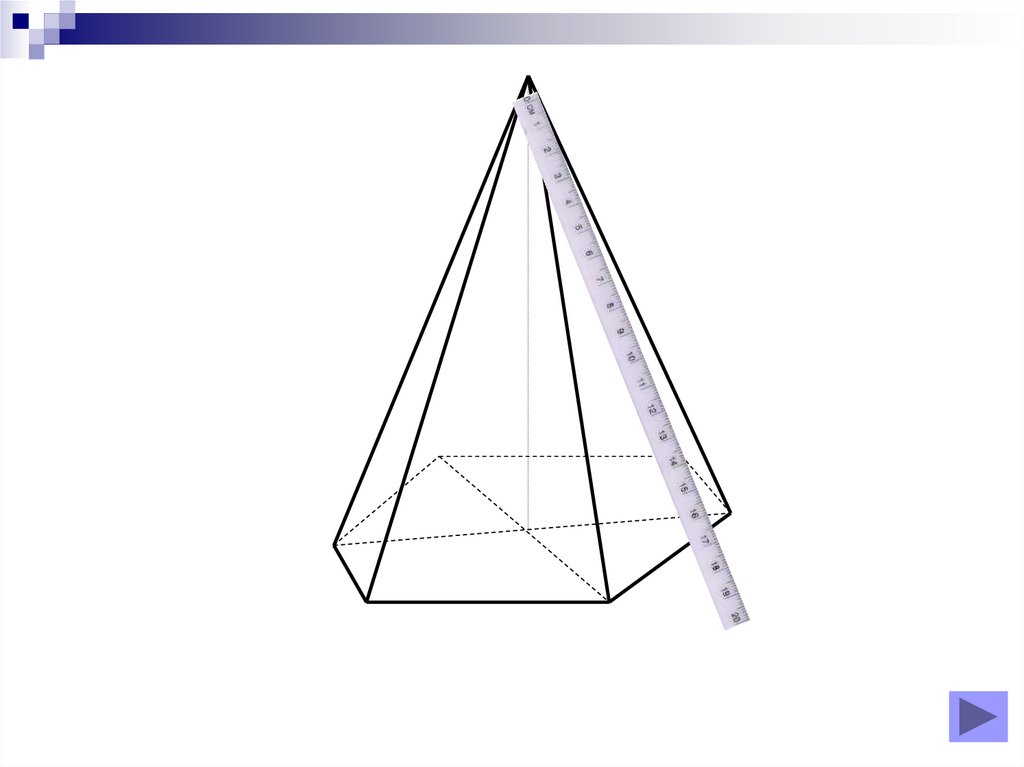
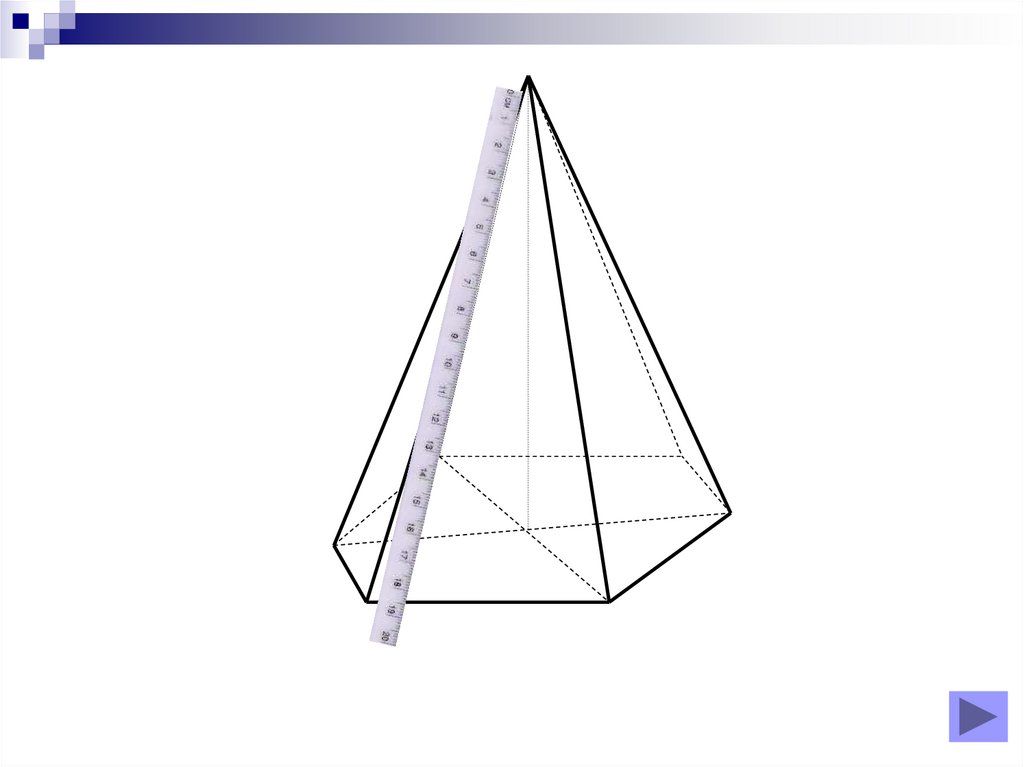
8. Diapozitivul 8

Piramidă triunghiulară regulată

9. Diapozitivul 9

10. Diapozitivul 10

11. Diapozitivul 11

12. Diapozitivul 12

13. Diapozitivul 13

14. Diapozitivul 14

15. Diapozitivul 15

16. Diapozitivul 16

17. Diapozitivul 17

18. Diapozitivul 18

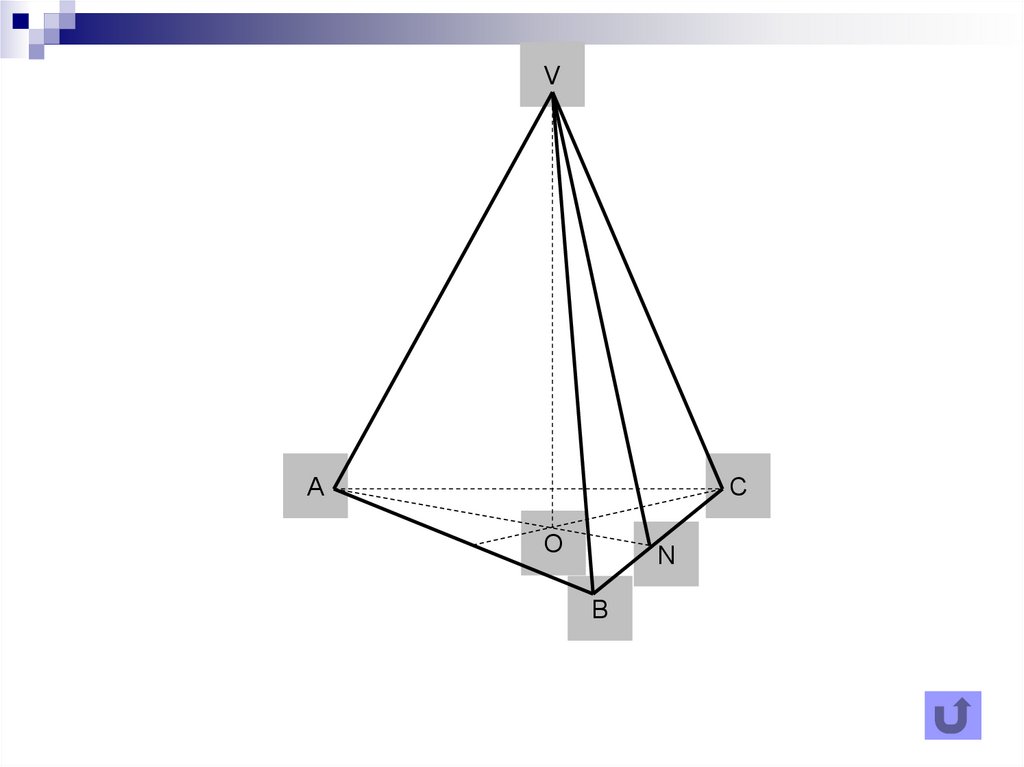
V
A
C
O
N
B

19. Diapozitivul 19

Piramidă patrulateră regulată

20. Diapozitivul 20

21. Diapozitivul 21

22. Diapozitivul 22

23. Diapozitivul 23

24. Diapozitivul 24

25. Diapozitivul 25

26. Diapozitivul 26

27. Diapozitivul 27

28. Diapozitivul 28

29. Diapozitivul 29

30. Diapozitivul 30

31. Diapozitivul 31

32. Diapozitivul 32

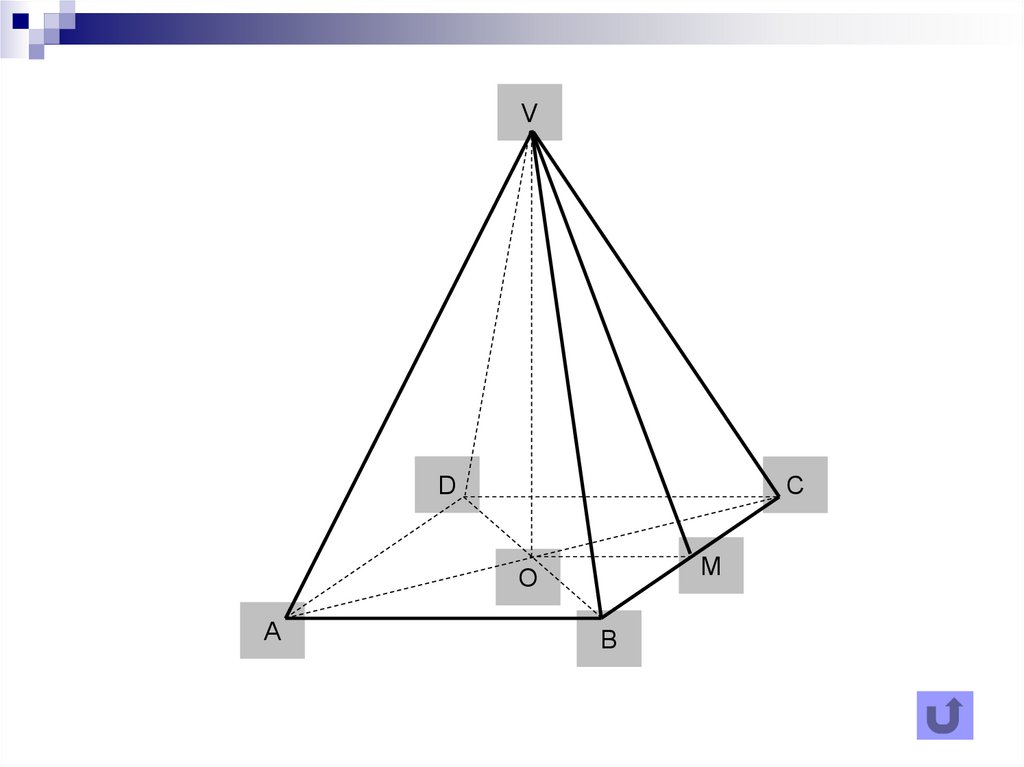
V
D
C
M
O
A
B

33. Diapozitivul 33

Piramidă hexagonală regulată

34. Diapozitivul 34

35. Diapozitivul 35

36. Diapozitivul 36

37. Diapozitivul 37

38. Diapozitivul 38

39. Diapozitivul 39

40. Diapozitivul 40

41. Diapozitivul 41

42. Diapozitivul 42

43. Diapozitivul 43

44. Diapozitivul 44

45. Diapozitivul 45

46. Diapozitivul 46

47. Diapozitivul 47

48. Diapozitivul 48

49. Diapozitivul 49

50. Diapozitivul 50

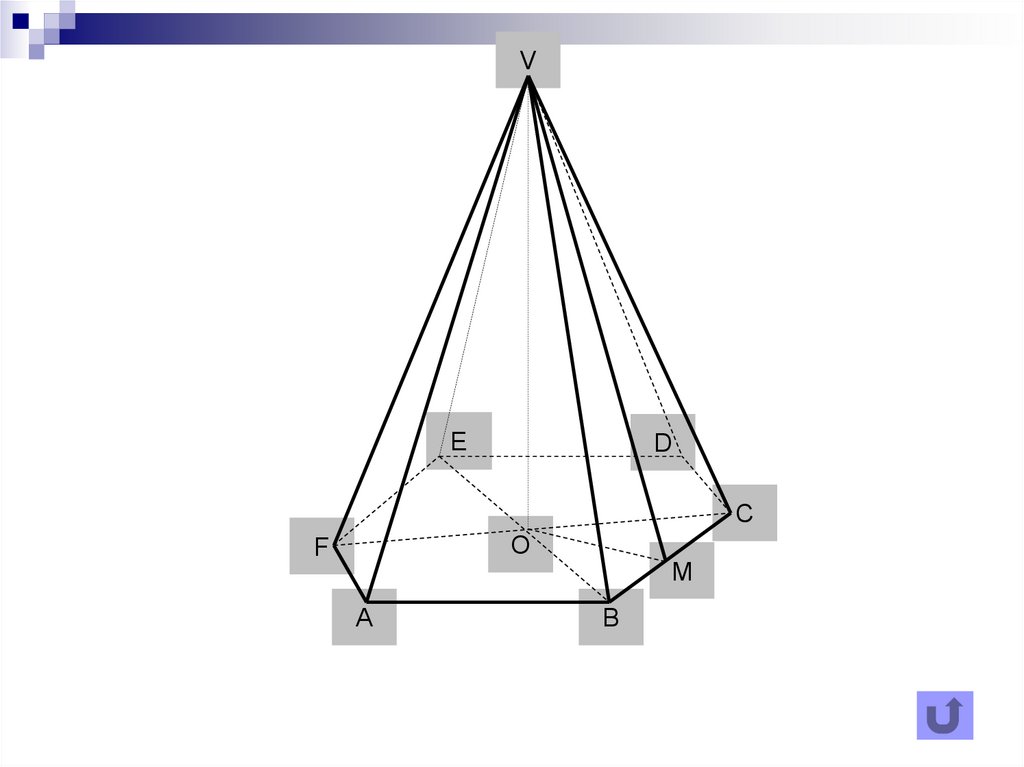
V
E
D
C
O
F
M
A
B

51. Diapozitivul 51

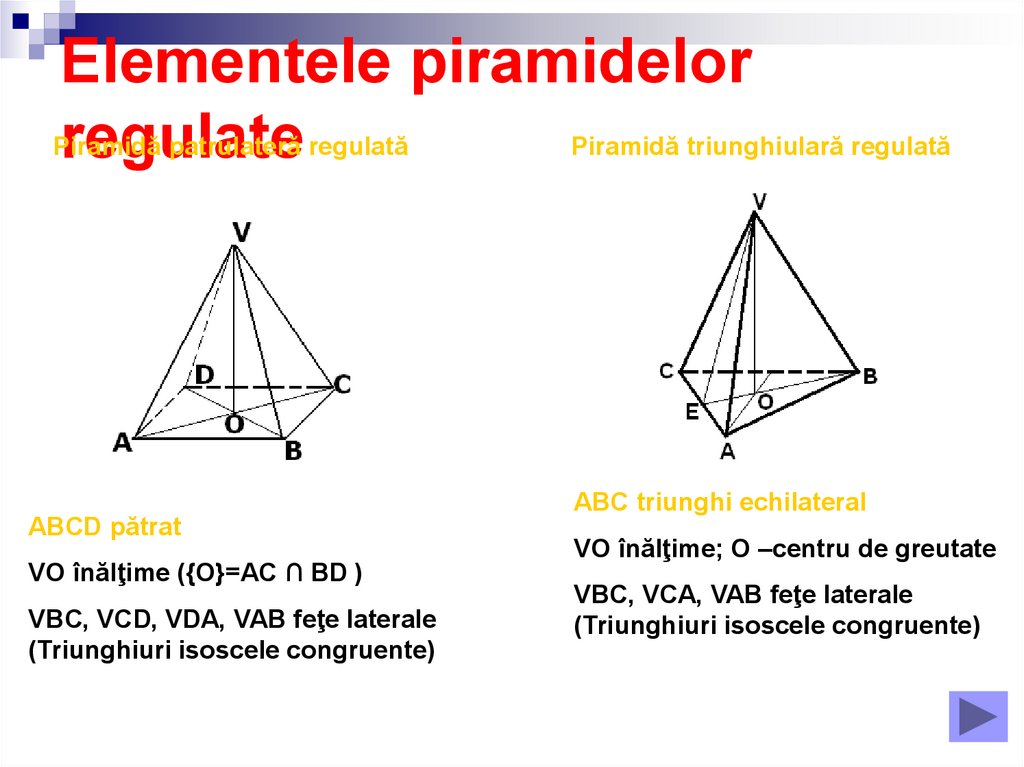
Elementele piramidelor
Piramidă
patrulateră regulată
Piramidă triunghiulară regulată
regulate
ABCD pătrat
VO înălţime ({O}=AC ∩ BD )
VBC, VCD, VDA, VAB feţe laterale
(Triunghiuri isoscele congruente)
ABC triunghi echilateral
VO înălţime; O –centru de greutate
VBC, VCA, VAB feţe laterale
(Triunghiuri isoscele congruente)

52. Elementele piramidelor regulate

Triunghiuri de lucru în
piramida triunghiulară regulată
Fie AB AC BC a muchia bazei
VO h
VE Ap apotema
piramidei
OE ap apotema bazei
VB l muchie laterală
1 a 3
VOE : OE
; VO 2 OE 2 VE 2
3 2
2 a 3
VOB :OB
; VO 2 OB 2 VB 2
3 2
a
VEA : EA ; VE 2 EA2 VA2
2

53. Triunghiuri de lucru în piramida triunghiulară regulată

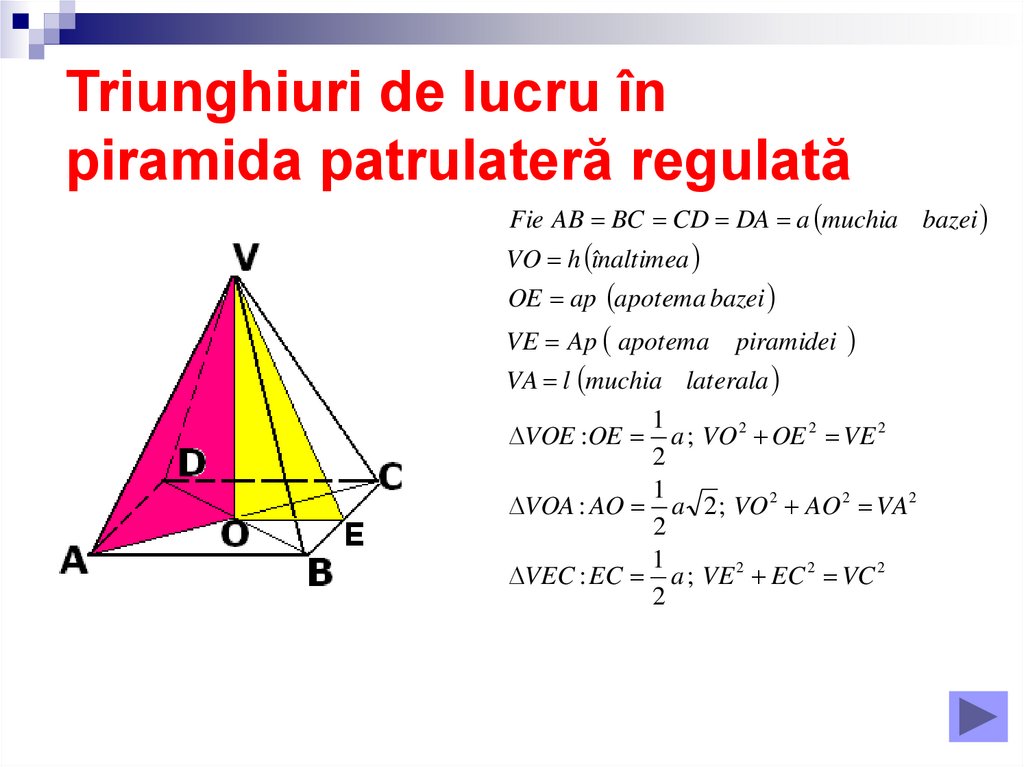
Triunghiuri de lucru în
piramida patrulateră regulată
Fie AB BC CD DA a muchia bazei
VO h înaltimea
OE ap apotema bazei
VE Ap apotema
piramidei
VA l muchia laterala
1
a ; VO 2 OE 2 VE 2
2
1
VOA : AO a 2 ; VO 2 AO 2 VA2
2
1
VEC : EC a ; VE 2 EC 2 VC 2
2
VOE :OE

54. Triunghiuri de lucru în piramida patrulateră regulată

Triunghiuri de lucru în
piramida hexagonală regulată
Fie AB BC BD ... EF a muchia bazei
VO h înaltimea piramidei
OM ap apotema
VM Ap
bazei
apotema piramidei
VA VB VC ... VE VF l muchii laterale
a 3
; VO 2 OM 2 VM 2
2
EB
VOE : OE
a; VO 2 OE 2 VE 2
2
a
VMA : AM ; VM 2 MA 2 VA2
2
VOM : OM

55. Triunghiuri de lucru în piramida hexagonală regulată

Al= arie laterală=suma ariilor feţelor
laterale
At= arie totală = Al + aria bazei
At = Al + Abază
1
V volum Abazei înaltime
3

56. Diapozitivul 56

Formule de calcul pentru piramide
regulate
Pbazei Apotemă
Al
2
1
V Abaza h
3
At Al Abază
pentru orice tip de piramidă

57. Diapozitivul 57

Piramidă triunghiulară regulată cu muchia bazei “a”
Pbaza 3a
a2 3
Abaza
4
Piramidă patrulateră regulată cu muchia bazei “a”
Pbaza 4a
Abaza a 2
Piramidă hexagonală regulată cu muchia bazei “a”
Pbaza 6a
a2 3
Abaza 6
4

58. Diapozitivul 58

59. Diapozitivul 59

1. Fie VABCD o piramidă patrulateră regulată. Dacă se
cunoaşte muchia bazei AB=4 cm, înălţimea VO=12 cm, să se
calculeze aria şi volumul.
R1
2. Dacă muchia laterală a unei piramide patrulatere regulate
este de 10 cm, iar muchia bazei de 12 cm, să se calculeze
volumul şi aria lateralã.
R2

60. Diapozitivul 60

1
Ab h , unde Ab a 2 , Ab 4 2 16(cm 2 ).
3
1
Deci V 16 12 64(cm 3 ).
3
VOE : VO 2 OE 2 VE 2
Avem V
12 2 2 2 VE 2
144 4 VE 2
VE 148 2 37 Ap p 2 37cm.
A Al Ab ; Al
1
Pb Ap p
2
1
16 2 37 16 37 (cm 2 )
2
A 16 37 16 16 1 37 cm 2
Al

61. Diapozitivul 61

AB BC CD DA 12cm EC 6cm
VEC : VC 10cm, EC 6cm VE 8cm. numere pitagorice
VOE : OE
AB
6cm VO 2 VE 2 OE 2
2
VO 2 64 36 VO 28 2 7cm
1
1
V Ab h 144 2 7 72 7 (cm 3 )
3
3
1
1
Al Pb Ap 48 8 192(cm 2 )
2
2

62. Diapozitivul 62

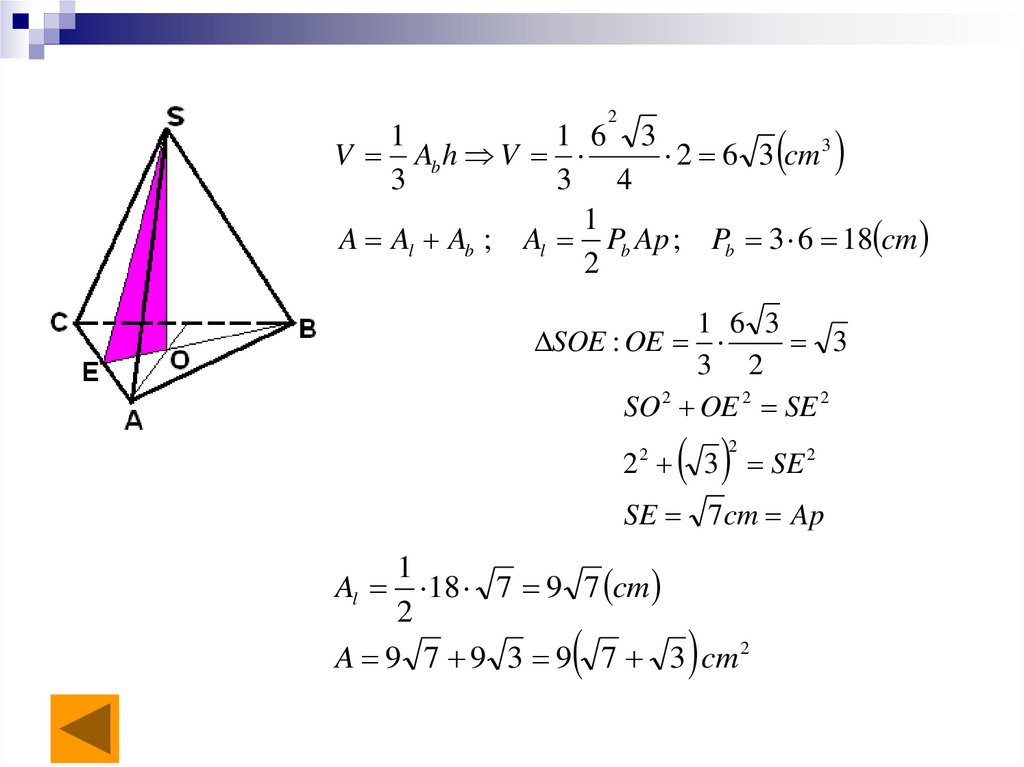
1. Fie SABC o piramidă triunghiulară regulată cu
muchia bazei AB=6 cm şi înălţimea SO=2 cm. Să se
calculeze aria şi volumul piramidei!
R
2. Fie VABC o piramidă triunghiulară regulată. Dacă
se cunoaşte muchia VB=10 cm, înălţimea VO=8 cm
să se calculeze aria şi volumul piramidei!
R

63. Diapozitivul 63

2
1
1 6 3
V Ab h V
2 6 3 cm 3
3
3 4
1
A Al Ab ; Al Pb Ap ; Pb 3 6 18 cm
2
1 6 3
SOE : OE
3
3 2
SO 2 OE 2 SE 2
2
2
3
2
SE 2
SE 7cm Ap
1
18 7 9 7 cm
2
A 9 7 9 3 9 7 3 cm 2
Al

64. Diapozitivul 64

VOB : VO 2 OB 2 VB 2 OB 2 100 64 OB 36 6(cm)
dar OB
2 AB 3
18
AB
6 3 (cm)
3
2
3
1
1 6 3
V AABC VO V
3
3
4
VC 10cm
2
3
8 72 3 (cm3 )
2
2
2
2
2
2
VEC :
VE
VC
EC
VE
10
3
3
VE 73 cm Ap
6 3
EC
cm
2
A Al Ab A
1
1
Pb h Ab A 18 3 73 27 3 9 3 73 3 (cm 2 )
2
2