Similar presentations:
Aproximarea numerică a funcţiilor. Metode numerice – curs 11
1.
METODE NUMERICE – curs 11Cap. 7 Aproximarea numerică a funcţiilor
7.4 Derivarea numerică
fie funcţia
f : [a , b] , a , b , f f ( x ) şi divizarea a intervalului [a, b]:
[a , b] : a x 0 x i x n b
notaţie:
f i f ( x i ), i 0, , n
problema derivării numerice aproximarea valorilor derivatelor funcţiei f:
f ( x * ), f ( x * ), x * [a , b]
utilizând setul de valori:
{x i , f ( x i )}i 0,...,n
{x i }i 0,...,n , x i [a , b], i 0, , n
soluţia se determină o funcţie de tip polinomial care aproximează f
se evaluează derivata sa în diverse puncte din intervalul [a, b]
aplicabil primele două derivate dacă datele sunt afectate de eroare (de exemplu, zgomot de
măsură), atunci operaţia de derivare tinde să amplifice aceste erori.
2.
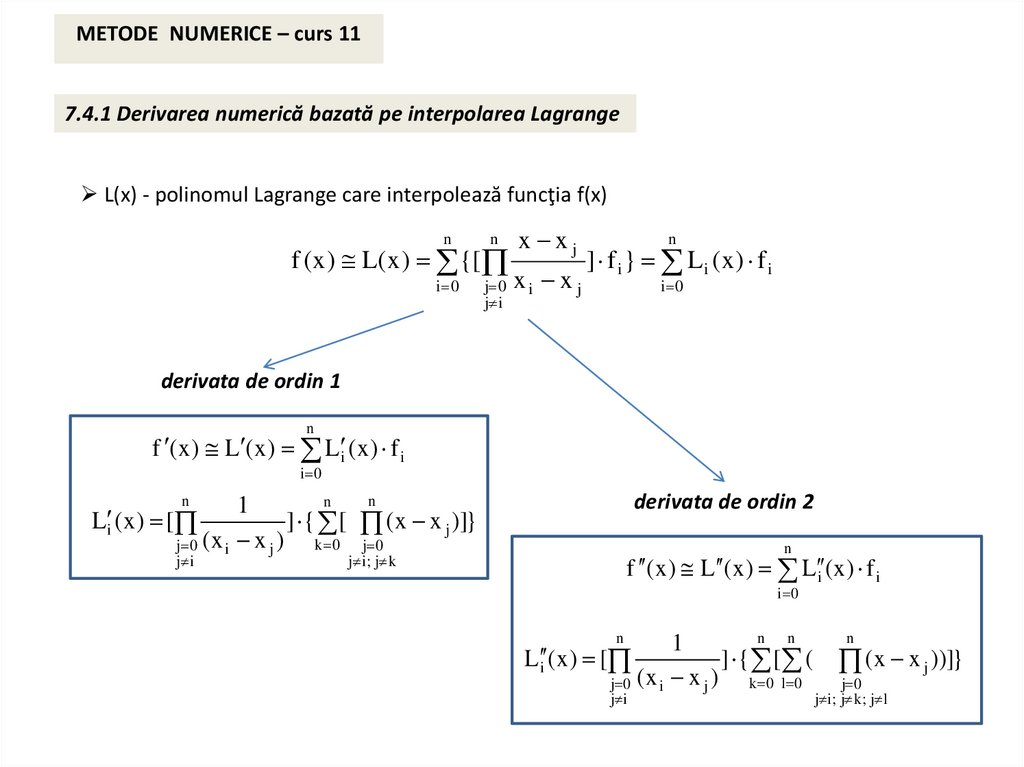
METODE NUMERICE – curs 117.4.1 Derivarea numerică bazată pe interpolarea Lagrange
L(x) - polinomul Lagrange care interpolează funcţia f(x)
n
n
f ( x ) L( x ) {[
i 0
x xj
j 0 x i x j
n
] f i } L i (x) f i
i 0
j i
derivata de ordin 1
n
f ( x ) L ( x ) L i ( x ) f i
i 0
derivata de ordin 2
n
n
n
1
L i ( x ) [
] { [ ( x x j )]}
k 0 j 0
j 0 ( x i x j )
j i
n
f ( x ) L ( x ) L i ( x ) f i
j i ; j k
i 0
n
n
n
1
L i ( x ) [
] { [ (
k 0 l 0
j 0 ( x i x j )
j i
n
( x x j ))]}
j 0
j i ; j k ; j l
3.
METODE NUMERICE – curs 117.4.2 Formule de derivare numerică bazate pe interpolarea cu funcţii spline cubice
fie s ( x ) - funcţia spline cubică naturală care interpolează funcţia f
pentru x * [a , b]
f ( x * ) s ( x * )
*
trebuie identificat intervalul [ x i , x i 1 ] unde se află argumentul x
s (x) [ x
i , x i 1 ]
f ( x * ) s ( x * )
f ( x * ) s ( x * )
[ x i , x i 1 ]
a i (x x i )3 bi (x x i ) 2 ci (x x i ) d i
[ x i , x i 1 ]
3 a i (x * x i ) 2 2 b i (x * x i ) ci
f ( x i ) c i
6 a i ( x * x i ) 2 b i , f ( x i ) 2 b i
pentru aproximarea derivatelor de ordin superior, se folosesc funcţii spline de ordin
mai mare decât 3 pentru aproximarea funcţiei f
4.
METODE NUMERICE – curs 117.5 Cuadratura numerică
funcţia f : [a , b] , f f ( x ) , cunoscută prin intermediul setului de puncte:
{x i , f i }i 0, ,n , f i f ( x i )
a x 0 x 1 x i x i 1 x n b
b
problema de calculul determinarea valoarii integralei definite I(f ) f ( x ) dx
a
n 1
x i 1
i 0
xi
I(f ) I i (f ), I i (f )
f ( x ) dx,
i 0, , n 1
spre deosebire de operaţia de derivare numerică, cuadratura tinde să “netezească” sau să
diminueze erorile ce afectează datele.
Definiţii:
Se numeşte regulă (elementară) de cuadratură, o formulă simplă care aproximează valorile
integralelor elementare .
Se numeşte regulă compusă de cuadratură, o formulă care aproximează valoarea integralei
definite , ca o sumă a regulilor (elementare) de cuadratură.
5.
METODE NUMERICE – curs 117.5.1 Regula dreptunghiului
funcţia f(x) este aproximată pe intervalul [ x i , x i 1 ] printr-un polinom de gradul zero:
f ( x ) f (( x i x i 1 ) / 2)
y
y f (x)
x x i 1
I i (f ) D i (f ) h i f i
, h i x i 1 x i , i 0, , n 1
2
f ( x i 1 )
f(
x i x i 1
)
2
f (x i )
n 1
n 1
x x i 1
I(f ) D (f ) D i (f ) h i f i
2
i 0
i 0
x
0
xi
x i 1
x i x i 1
2
f nu este cunoscută analitic
se vor considera trei perechi de puncte cu
abscisele echidistante:
h i x i 1 x i
( x i 1 , f i 1 ), ( x i , f i ), ( x i 1 , f i 1 )
D i (f ) ( x i 1 x i 1 ) f ( x i )
e D (f ) I(f ) D(f ), | e D (f ) |
b a 2
h f ( ), (a , b)
12
6.
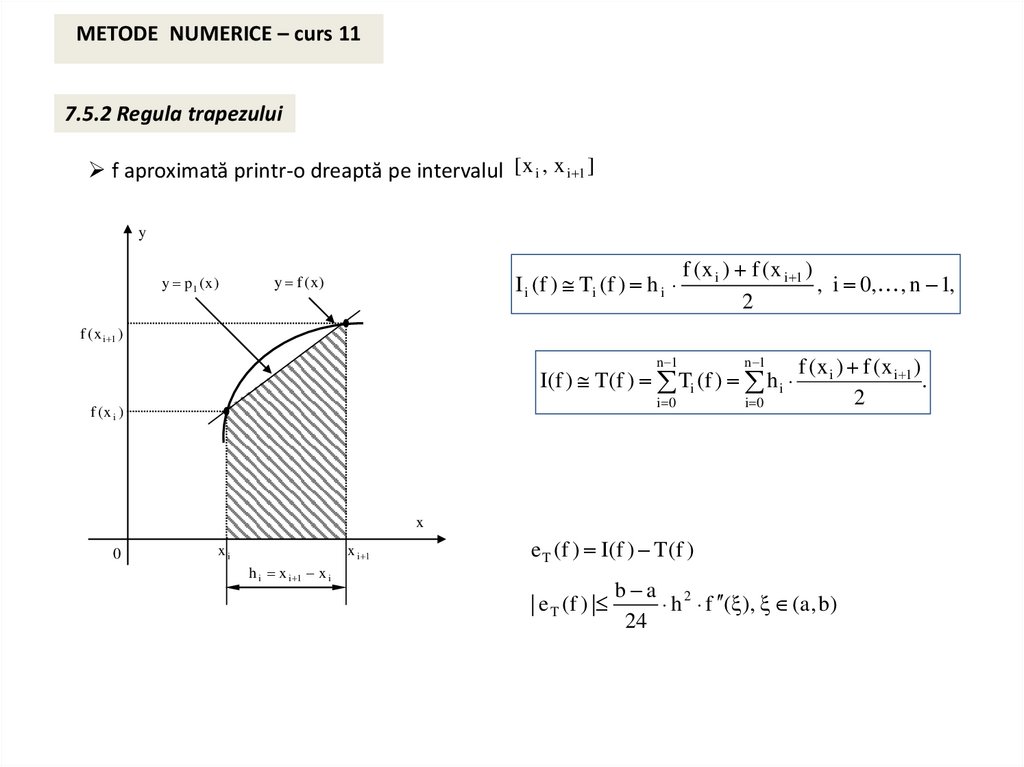
METODE NUMERICE – curs 117.5.2 Regula trapezului
f aproximată printr-o dreaptă pe intervalul [ x i , x i 1 ]
y
y p1 ( x )
I i (f ) Ti (f ) h i
y f (x)
f ( x i ) f ( x i 1 )
, i 0, , n 1,
2
f ( x i 1 )
n 1
n 1
i 0
i 0
I(f ) T (f ) Ti (f ) h i
f (x i )
f ( x i ) f ( x i 1 )
.
2
x
0
xi
x i 1
h i x i 1 x i
e T (f ) I(f ) T (f )
| e T (f ) |
b a 2
h f ( ), (a , b)
24
7.
METODE NUMERICE – curs 117.5.3 Regula Simpson
f aproximată printr-un polinom de gradul al doilea ce trece prin punctele:
{x i , f ( x i )}, {
x i x i 1 x i x i 1
,f
}, {x i 1 , f ( x i 1 )}
2
2
y
y f (x)
S i (f )
1
x x i 1
h i f ( x i ) 4 f i
f ( x i 1 ) , i 0, , n 1,
6
2
n 1
n 1 1
x x i 1
I(f ) S(f ) Si (f ) h i f ( x i ) 4 f i
f ( x i 1 ) .
2
i 0
i 0 6
y p 2 (x)
x
0
xi
x i x i 1
2
h i x i 1 x i
x i 1
e S (f ) I(f ) S(f ), | e S (f ) |
1 n 1 5 ( 4) x i x i 1
hi f
2850 i 0
2
8.
METODE NUMERICE – curs 11f nu este cunoscută analitic
se vor considera trei perechi de puncte cu
abscisele echidistante:
S i (f )
( x i 1 , f i 1 ), ( x i , f i ), ( x i 1 , f i 1 )
2
1
D i (f ) Ti (f )
3
3
se consideră divizarea intervalului [a, b] ca fiind formată din puncte echidistante:
h x i 1 x i ,
i 0, , n 1
dezvoltări particulare:
n - impar
regula 1/3 Simpson
n - par
regula 3/8 Simpson
h
(f 0 4 f 1 f 2 f 2 4 f 3 f 4 )
3
h
(f 0 4 f 1 2 f 2 4 f n 3 2 f n 2 4 f n 1 f n ).
3
S(f )
3 h
(f 0 3 f 1 3 f 2 2 f 3 3 f 4 3 f 5
8
2 f n 3 3 f n 2 3 f n 1 f n ).
S(f )
9.
METODE NUMERICE – curs 117.5.4 Cuadratura bazată pe interpolarea cu funcţii spline cubice
se utilizează rezultatele aproximării funcţiei f prin interpolare cu funcţii spline cubice (naturale)
n 1 1
1
1
I(f ) f ( x ) dx h i4 a i h 3i b i h i2 c i h i d i
3
2
i 0 4
a
b
h i x i 1 x i , i 0, , n 1
ţinând cont de expresiile coeficienţilor ai, bi, ci, di:
n 1
f (x ) f (x )
b b
f
(
x
)
dx
h i i 2 i 1 h 3i i 12 i 1
i 0
a
b
faţă de formula trapezului, apare în plus termenul h 3i (b i b i 1 ) / 12
creşte precizia aproximării
10.
METODE NUMERICE – curs 11Cap. 8 Ecuaţii diferenţiale ordinare cu condiţii iniţiale
8.1 Formularea problemei
8.1.1 Ecuaţii diferenţiale ordinare de ordinul întâi
fie o funcţie reală de două variabile reale:
f f ( t , y( t ))
y : [a, b] I , f : [a, b] I R
t [a , b ]
- variabilă independentă
y y( t )
- variabilă dependentă
se consideră ecuaţia diferenţială de ordinul întâi de forma:
problema Cauchy
dy( t )
f ( t , y( t ))
dt
y 0 y( t 0 ), t 0 [a , b], y 0 I
(1)
t0 a
(2)
condiţia iniţială
Problema de calcul determinarea soluţiei (aproximative), y(t), a ecuaţiei diferenţiale (1),
cu condiţia iniţială (2), pentru orice valoare a argumentului t [a , b]
11.
METODE NUMERICE – curs 11Teoremă:
Fie ecuaţia (1) şi condiţia iniţială (2). Dacă sunt îndeplinite condiţiile:
funcţia f este continuă în raport cu argumentul t [a , b];
funcţia f este lipschitziană în raport cu argumentul y I , anume L 0 astfel încât este
îndeplinită relaţia:
t [a , b], y1 , y 2 I, | f ( t , y1 ) f ( t , y 2 ) | L | y1 y 2 |
atunci există şi este unică o soluţie a problemei Cauchy.
metodele numerice de rezolvare a problemei Cauchy discretizează intervalul [a,b] într-o reţea de
puncte distincte şi anume:
[ a ,b ] : a t 0 t 1 t i 1 t i t N b
prin anumite formule de recurenţă se calculează yi, drept aproximaţii ale soluţiei exacte y(ti),
având drept punct de start valoarea precizată y0: y( t i ) y i , i 1, N
{y 0 , y 1 , , y N }
soluţia numerică a problemei Cauchy
h i t i 1 t i , i 0,1,..., N 1
[t 0 , t N ]
pas de observare
paşi de integrare
12.
METODE NUMERICE – curs 118.1.2 Ecuaţii diferenţiale ordinare de ordin superior
ecuaţii diferenţiale ordinare de ordinul n
d n y( t )
d n 1 y( t )
dy( t )
an
a
a
a 0 y( t ) b 0 u ( t ),
n 1
1
dt
dt n
dt n 1
a i , b 0 , i 0,1,..., n; a n 0
y( t 0 ), y (1) ( t 0 ),..., y ( n 1) ( t 0 ), t 0 [a , b]
u(t)
(3)
condiţiile iniţiale cunoscute
cunoscută analitic sau printr-un şir de valori
pentru rezolvarea numerică a acestei ecuaţii se transformă într-un sistem
de n ecuaţii diferenţiale ordinare, fiecare ecuaţie fiind de ordinul întâi
metodele pentru rezolvarea ecuaţiilor diferenţiale de ordinul întâi se
extind la cazul sistemelor de ecuaţii diferenţiale
13.
METODE NUMERICE – curs 11ecuaţia (3) se rescrie sub forma:
d n y( t )
dt n
notaţii:
a0
a 1 dy( t )
a n 1 d n 1 y( t ) b 0
y( t )
u(t)
an
an
dt
an
an
dt n 1
k a n k / a n , k 1,..., n; n b 0 / a n
x 1 ( t ) y( t ),
dy( t ) dx 1 ( t )
x 1 ( t )
dt
dt
d 2 y( t ) dx 2 ( t )
x 3 (t)
x 2 ( t )
2
dt
dt
x 2 (t)
se definesc urmoarele variabile de lucru:
x n (t)
x 1 ( t ) x 2 ( t )
x ( t ) x ( t )
3
2
x ( t ) x ( t )
n
n 1
x n ( t ) n x 1 ( t ) n 1 x 2 ( t ) 1 x n ( t ) n u ( t )
d n 1 y( t )
dt n 1
dx n 1 ( t )
x n 1 ( t )
dt
y( t ) x 1 ( t )
14.
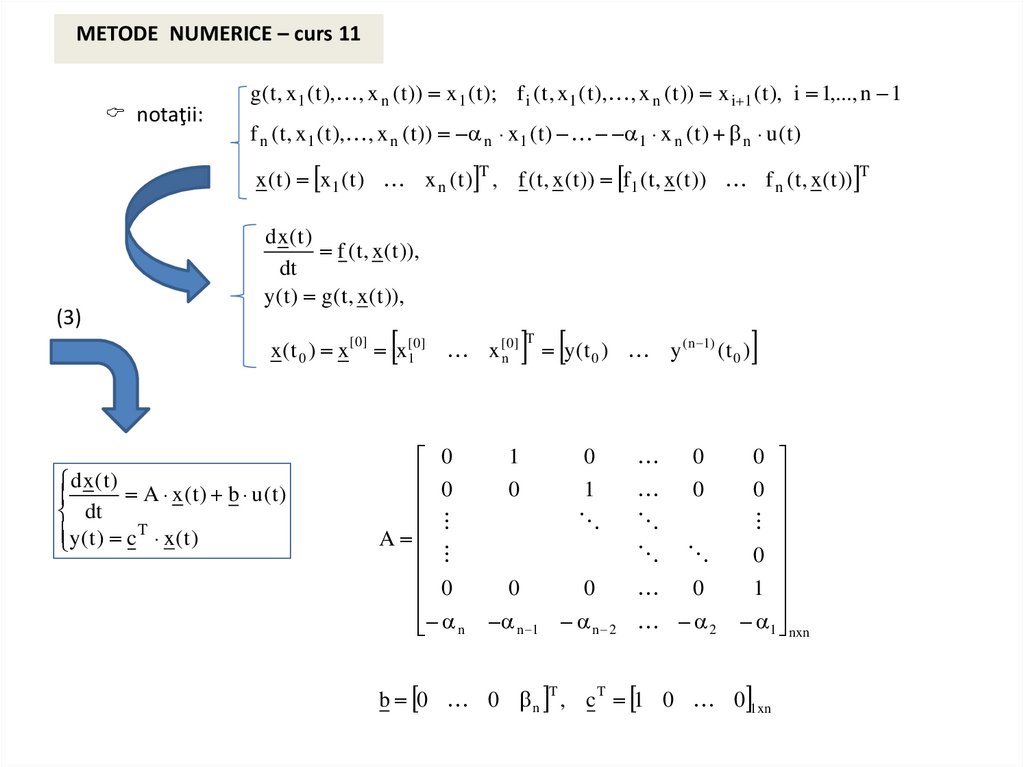
METODE NUMERICE – curs 11notaţii:
g ( t , x 1 ( t ), , x n ( t )) x 1 ( t ); f i ( t , x 1 ( t ), , x n ( t )) x i 1 ( t ), i 1,..., n 1
f n ( t , x 1 ( t ), , x n ( t )) n x 1 ( t ) 1 x n ( t ) n u ( t )
x ( t ) x 1 ( t ) x n ( t ) T , f ( t , x ( t )) f1 ( t , x ( t )) f n ( t , x ( t )) T
(3)
d x(t)
f ( t , x ( t )),
dt
y( t ) g ( t , x ( t )),
x(t 0 ) x
d x(t)
A x(t) b u(t)
dt
y( t ) c T x ( t )
[0]
x1[ 0] x [n0]
0
0
A
0
n
y(t )
T
0
y ( n 1) ( t 0 )
1
0
0
0
1
0
0
0
n 1
0
n 2 2
0
0
0
1
1 nxn
b 0 0 n , c 1 0 0 1xn
T
T











 mathematics
mathematics








