Класичне означення ймовірності

1.

Тема уроку:
Класичне
означення
ймовірності.
1

2.

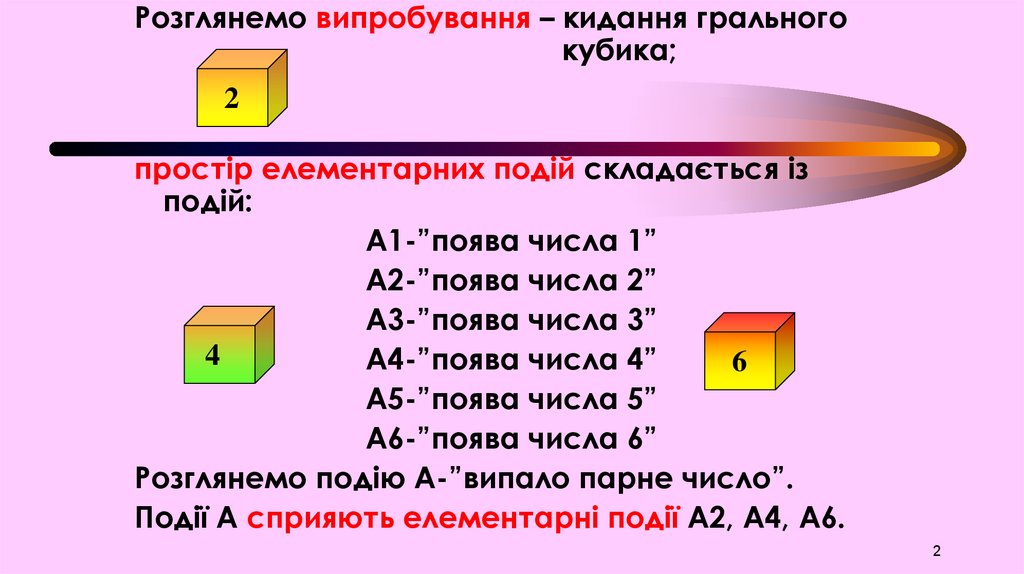
Розглянемо випробування – кидання грального
кубика;
2
простір елементарних подій складається із
подій:
А1-”поява числа 1”
А2-”поява числа 2”
А3-”поява числа 3”
4
А4-”поява числа 4”
6
А5-”поява числа 5”
А6-”поява числа 6”
Розглянемо подію А-”випало парне число”.
Події А сприяють елементарні події А2, А4, А6.
2

3.

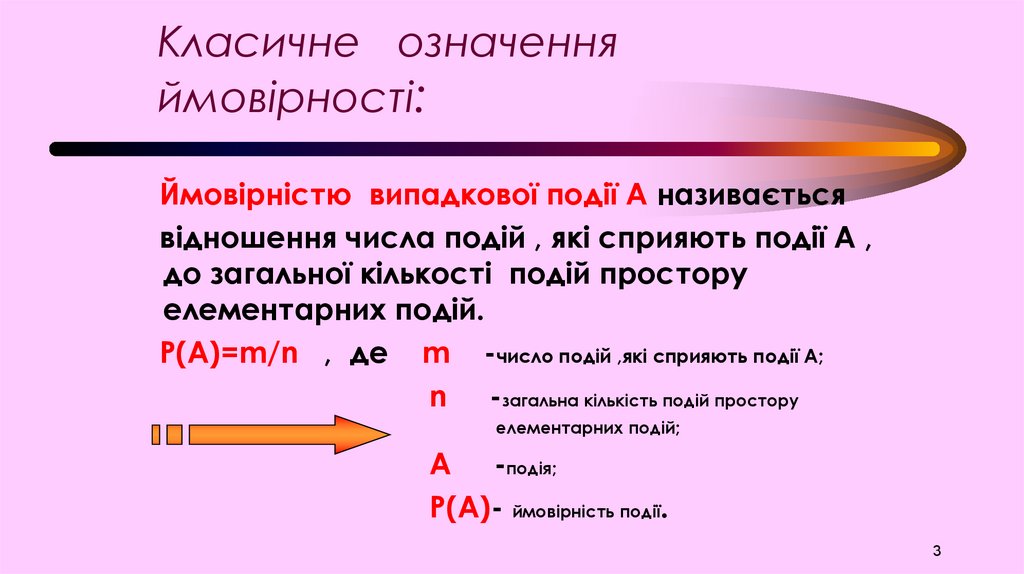
Класичне означення
ймовірності:
Ймовірністю випадкової події А називається
відношення числа подій , які сприяють події А ,
до загальної кількості подій простору
елементарних подій.
Р(А)=m/n , де m -число подій ,які сприяють події А;
n -загальна кількість подій простору
елементарних подій;
A -подія;
P(А)- ймовірність події.
3

4.

Приклад: знайти ймовірність того, що при
киданні двох монет випаде два герба.
Нехай подія А – “випало два герба”.
Простір елементарних подій :
А1 – “випало два герба”;
А2 – “випали герб та число”;
А3 – “випали число та герб”;
А4 – “випали два числа”.
Події А сприяє лише подія А1.
Отже, m = 1, n = 4 і тоді P ( A ) = m / n = 1/4= 0,25
Відповідь: 0,25.
4

5.

Використання
формул
комбінаторики для
обчислення
ймовірностей подій.
17.01.2021
5

6.

Безпосередній підрахунок ймовірностей подій
значно спрощується , якщо використовувати
формули комбінаторики.
Правильність розв’язання задачі
залежить від уміння визначити вид сполук,
що утворюються сукупністю подій, про які
йдеться мова в умові задачі.
Згадаємо алгоритм визначення виду
сполуки.
17.01.2021
6

7.

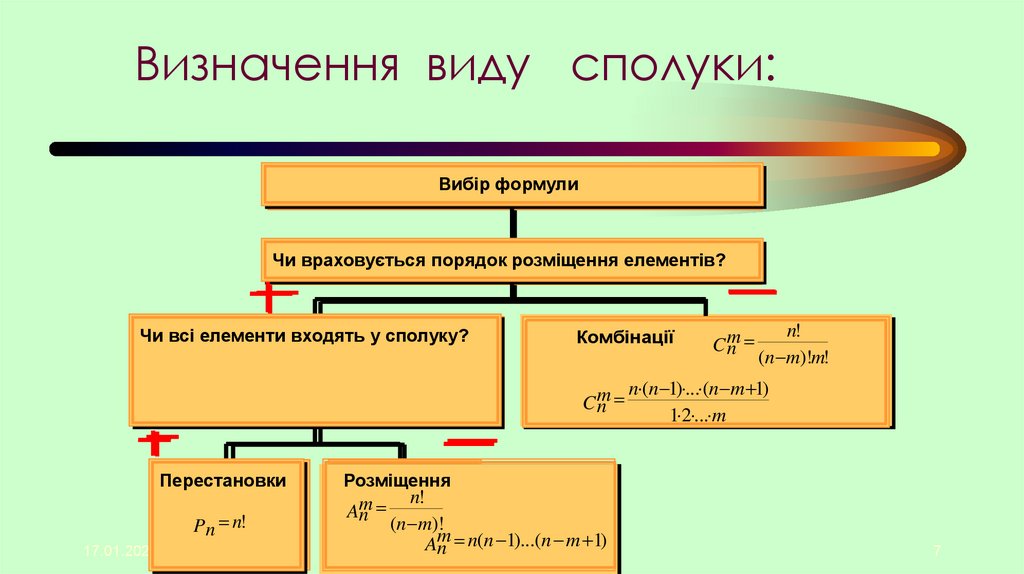
Визначення виду сполуки:
Вибір
Вибірформули
формули
Чи
розміщення
елементів?
Чивраховується
враховуєтьсяпорядок
порядок
розміщення
елементів?
Чи
входять
у сполуку?
Чивсі
всіелементи
елементи
входять
у сполуку?
Комбінації
Cm
n
n!
(n m)!m!
n (n 1) ... (n m 1)
m
Cn
1 2 ... m
Перестановки
Перестановки
Розміщення
Розміщення
n!n!
m
A
An (n m)!
(n m)!
Am
n n(n 1)...(n m 1)
m
n!n!
n
P nP
17.01.2021
n
7

8.

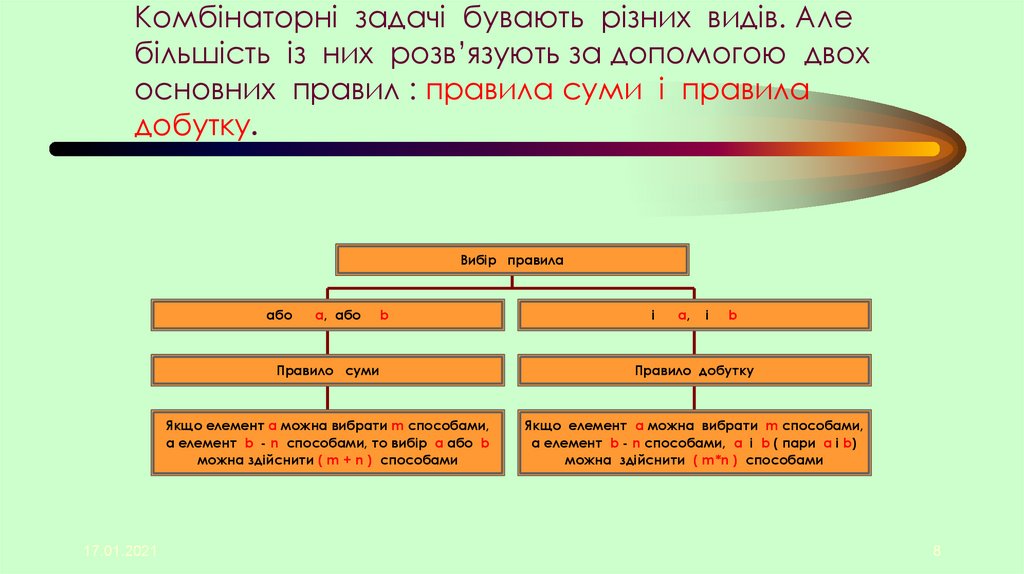
Комбінаторні задачі бувають різних видів. Але
більшість із них розв’язують за допомогою двох
основних правил : правила суми і правила
добутку.
Вибір правила
або
17.01.2021
a, або
b
і
a,
і
b
Правило суми
Правило добутку
Якщо елемент a можна вибрати m способами,
а елемент b - n способами, то вибір a або b
можна здійснити ( m + n ) способами
Якщо елемент a можна вибрати m способами,
а елемент b - n способами, a і b ( пари a і b)
можна здійснити ( m*n ) способами
8

9.

Задача 1. В урні лежать 20 кульок, з яких 12 білих,
решта- чорні. З урни навмання виймають дві кульки.
Яка ймовірність того, що вони білі?
Загальна кількість елементарних подій випробування “вийнято дві
кульки” дорівнює числу способів, якими можна вийняти 2 кульки
із 20 , тобто числу комбінацій із 20 елементів по 2
n C 220
Кількість елементарних подій, які сприяють події “ вийнято дві білих
кульки” дорівнює числу способів, якими можна вийняти 2 кульки
із 12 білих
2
m C 12
Ймовірність події А – “вийнято дві білі кульки” дорівнює
17.01.2021
2
m
12 11 1 2
33
C
P( A)
12
2
n
1 2 20 19 95
C 20
9

10.

Задача 2. В урні лежать 15 червоних, 9 синіх і 6 зелених
кульок однакових на дотик. Навмання виймають 6
кульок. Яка ймовірність того, що вийнято: 1 зелену, 2
синіх і 3 червоних кульок?
Випробування “із урни виймають 6 кульок із 30” (30= 15+9+6)
можна здійснити
способами.
6
n C 30
1
Одну зелену кульку можна вийняти C 6
способами.
Дві синіх кульки можна вийняти
2
C9
Три червоних кульки можна вийняти
способами.
3
C 15
способами.
Події А – “ вийнято 1 зелену і 2 синіх і 3 червоних кульки”
сприяють
3 2 1 елементарних подій.
m C15
C9 C6
17.01.2021
3
2
1
15 14 13 9 8 6 1 2 3 4 5 6
24
C
C
C
P( A) 15 69 6
1 2 3 1 2 30 29 28 27 26 25 145
C 30
10

11.

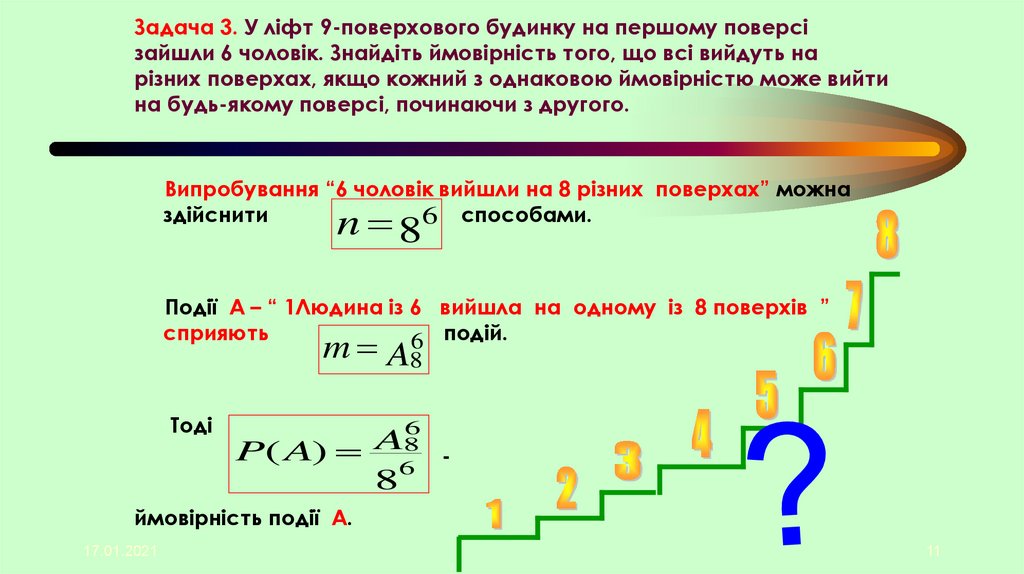
Задача 3. У ліфт 9-поверхового будинку на першому поверсі
зайшли 6 чоловік. Знайдіть ймовірність того, що всі вийдуть на
різних поверхах, якщо кожний з однаковою ймовірністю може вийти
на будь-якому поверсі, починаючи з другого.
Випробування “6 чоловік вийшли на 8 різних поверхах” можна
здійснити
6 способами.
n 8
Події А – “ 1Людина із 6 вийшла на одному із 8 поверхів ”
сприяють
6 подій.
m A8
Тоді
P( A)
6
A8
6
-
8
ймовірність події А.
17.01.2021
11