Similar presentations:
Теорія ймовірності
1.
2.
У сучасному світі автоматизації виробництва теорія ймовірностінеобхідна фахівцям для вирішення завдань, пов'язаних з
виявленням можливого перебігу процесів, на які впливають
випадкові фактори (наприклад, ВТК: скільки бракованих виробів
буде виготовлено). Виникла теорія ймовірності в 17 столітті в
листуванні Б. Паскаля і П. Ферма, де вони виробляли аналіз
азартних ігор. Радянські та російські вчені також брали участь у
розвитку цього розділу математики: П.Л. Чебишов, А.А. Марков,
А.М. Ляпунов, О.М. Колмогоров.
3.
Визначення1: Під випадковою подією розумієтьсявсяке явище, про яке має сенс
говорити, що воно відбувається або
не відбувається.
Подіями є результати різних дослідів, вимірювань, спостережень.
4.
Наприклад:1. З шухляди з різнокольоровими кульками
навмання виймають чорну кулю.
2. При киданні гральної кістки випала цифра 7.
3. При телефонному виклику абонент виявився
зайнятий.
4. Ви витягли чорну кулю.
5.
Визначення2: Вірогідною назвемо подію якаобов'язково станеться при виконанні
певної кількості умов (4 приклад).
Визначення3: Неможливою назвемо подію яка не
відбувається при виконанні певної
кількості умов (2 приклад).
Випадкові події позначаються великими латинськими літерами A, B, C, ...
6.
Визначення4: Дві події називаютьсянесумісними, якщо поява
одного з них виключає появу
іншого. В іншому випадку події
називаються сумісними.
7.
Приклади:1) При підкиданні монети поява цифри виключає
одночасної появи герба:
А поява
В поява
гербаГ ,
решкиР ,
несумісні
події .
2) Є квиток лотереї «Російське лото»:
А білет
В білет
виграшний ,
невиграшний,
несумісні
події .
8.
Виявляється, що при багаторазовому повторенні дослідучастота події приймає значення, близькі до деякого сталого
числа. Наприклад, при багаторазовому киданні гральної
кістки частота випадіння кожного з чисел очок від 1 до 6
1
коливається близько числа .
6
Багато разів проводилися досліди кидання однорідної
монети, в яких підраховували число появи «герба», і кожен
раз, коли число дослідів досить велике, частота1 події
«випадання герба» незначно відрізнялася від 2 .
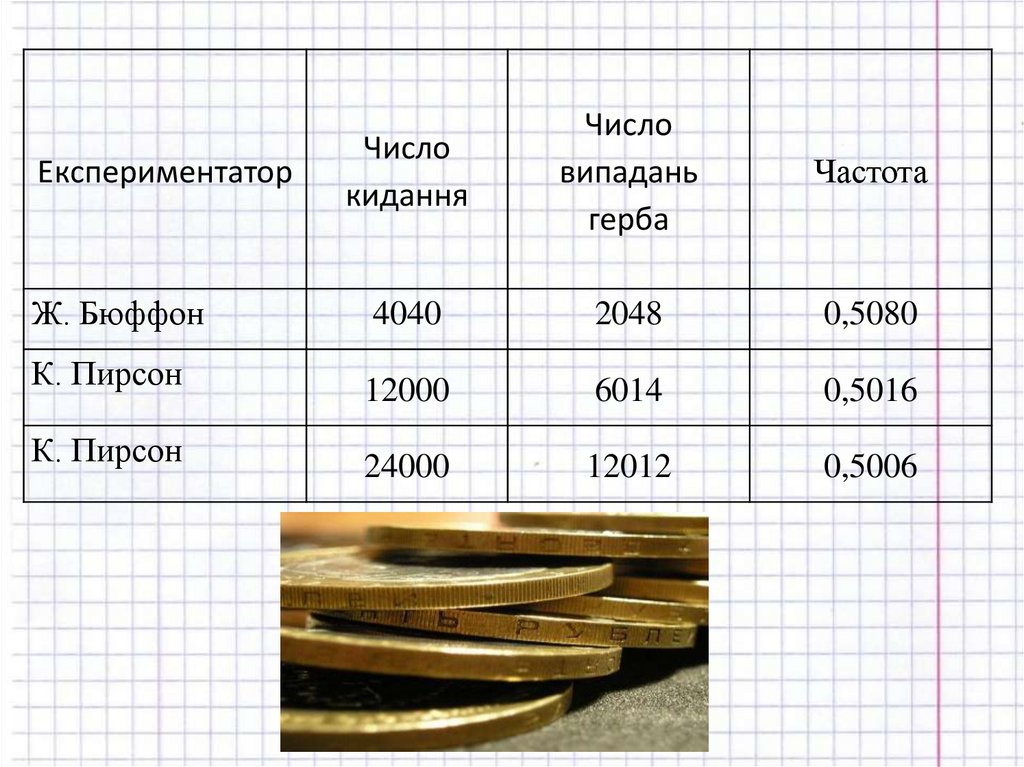
Для наочності розглянемо таблицю результатів, отриманих у
18 столітті французьким натуралістом Жоржем Луї Леклерк
Бюффоном (1707 - 1788) і на початку 20 століття англійським статистиком Карлом Пірсоном (1857 - 1936).
9.
Числокидання
Число
випадань
герба
Частота
Ж. Бюффон
4040
2048
0,5080
К. Пирсон
12000
6014
0,5016
К. Пирсон
24000
12012
0,5006
Експериментатор
10.
11.
1. В урні 3 білих і 9 чорних кульок. З урни навманнявиймається 1 кулю. Яка ймовірність того, що вийнята куля
виявиться білою?
Розв’язання:
Кількість всіх можливих результатів n = 3 +9 = 12.
Дослідів, в результаті яких може бути вийнята біла
куля m = 3.
m 3 1
P( А) 1.
n 12 4
Відповідь:
0, 25
12.
2. Кинута гральна кістка. Яка ймовірність подій: А-випало1 очко; В - випало 2 очки?
Розв’язання:
Кількість всіх можливих результатів n=6 (всі грані).
а) Кількість граней, на яких всього 1 очко m=1:
1
P ( A) 1,
6
б) кількість граней, на яких всього 2 очка m=1:
1
Відповідь:
6
1
і
.
6
1
P ( В ) 1.
6
13.
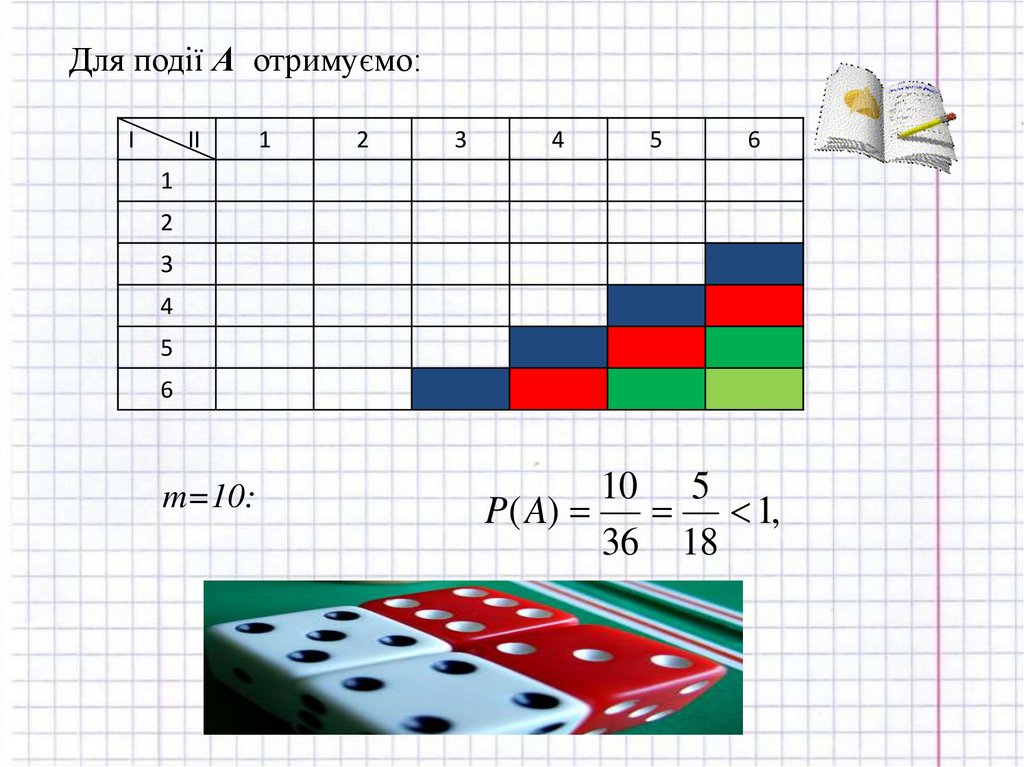
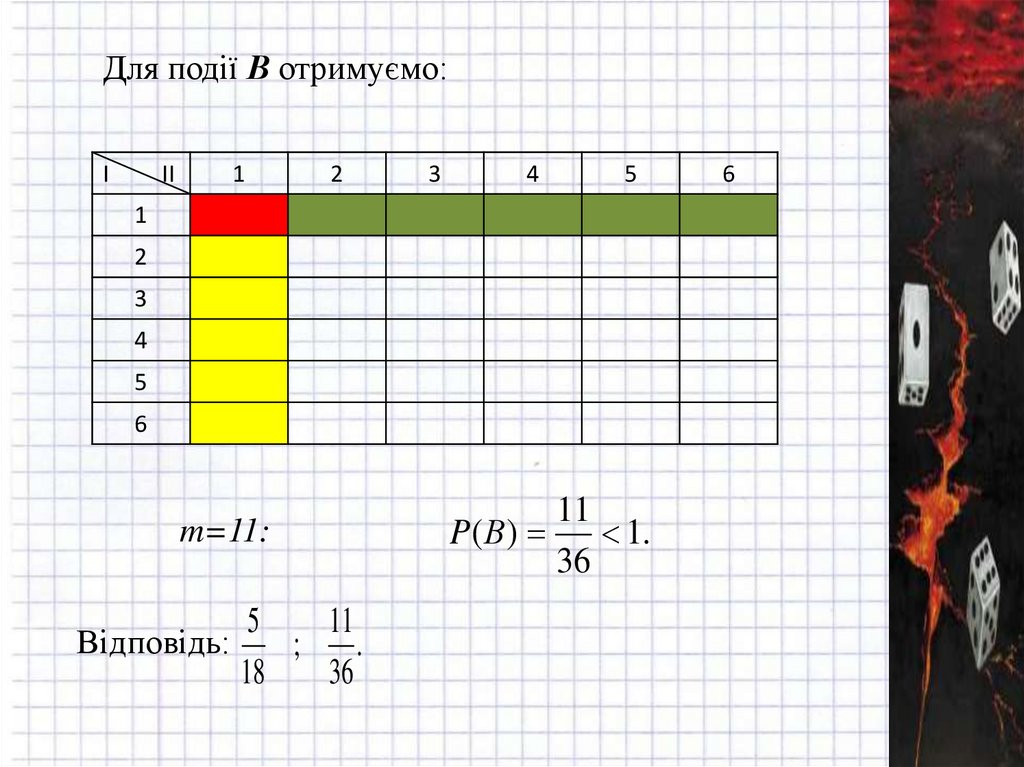
3. Кинуті 2 гральні кістки. Яка ймовірність подій: Авипадання в сумі не менше 9 очок; В - випадання 1 очкапринаймні на одній кістки?
Розв’язання:
I
II
1
2
3
4
5
1
2
3
4
5
6
Отримали, що можливо n = 36 результатів випробувань
6
14.
Для події А отримуємо:I
II
1
2
3
4
5
6
1
2
3
4
5
6
m=10:
10 5
P( A)
1,
36 18
15.
Для події В отримуємо:I
1
II
2
3
4
5
1
2
3
4
5
6
m=11:
Відповідь:
5
11
;
.
18
36
11
P( В)
1.
36
6
16.
4. Монета кинута 2 рази. Яка ймовірність події: А-випадепідряд два герби?
Розв’язання:
Скільки всього можливо результатів досліду?
ГГ,
ГР,
РГ,
РР
Таким чином, усього можливо результатів n = 4, нас
цікавить результат можливий тільки один раз m = 1,
тому
m 1
P( A) .
n 4
Відповідь: 0,25
17.
5. Набираючи номер телефону ви забули останню цифру інабрали її навмання. Яка ймовірність того, що набрана
потрібна вам цифра?
Розв’язання:
Скільки всього цифр? n=10
Ви забули тільки останню цифру, значить m=1
Тоді,
Відповідь:
P ( А)
0,1
m
1
0,1 1.
n 10
18.
6. З слова «математика» вибирається навмання однабуква. Яка ймовірність того, що це буде буква «м»?
Розв’язання:
n - кількість літер у слові, а m - кількість потрібної нам
букви «м».
m
2
P ( А)
0,2 1.
n 10
Відповідь:
0,2
19.
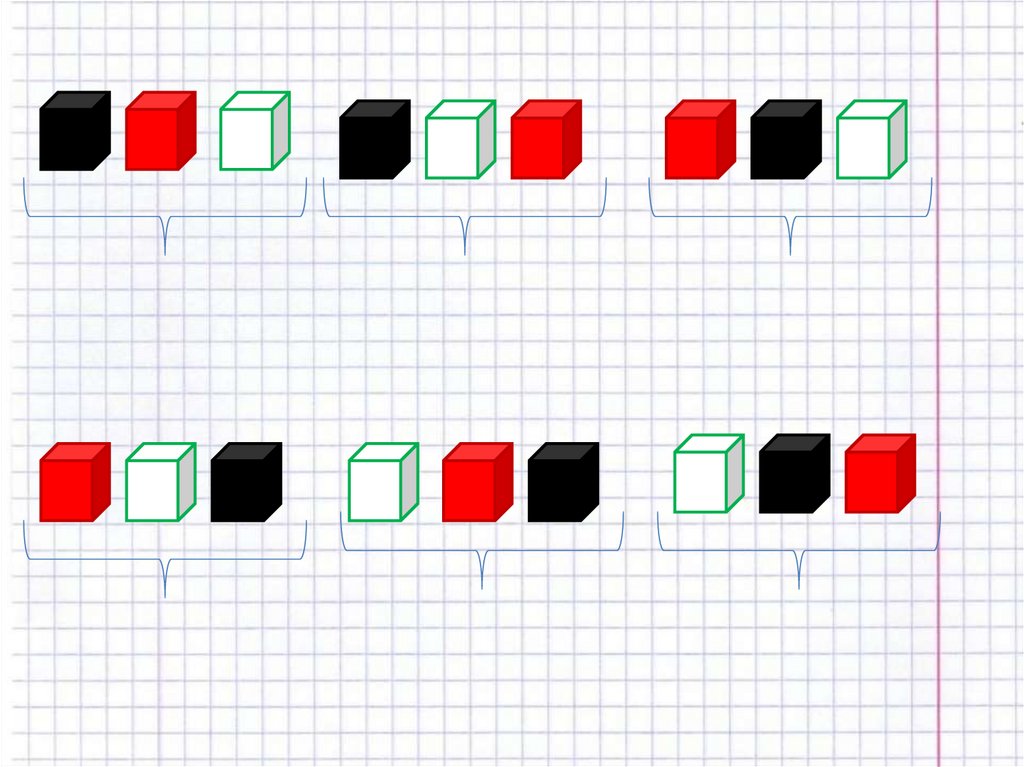
7. У коробці є 3 кубики: чорний, червоний та білий.Витягуючи кубики навмання, ми ставимо їх послідовно один
за одним. Яка ймовірність того, що в результаті вийде
послідовність: червоний, чорний, білий?
Розв’язання:
Скільки всього можливо результатів досліду? n=6
Нехай Ч - чорний кубик, К - червоний кубик, Б - білий
кубик, тоді
ЧКБ, ЧБК, БЧК, БКЧ, КЧБ, КБЧ.
P ( А)
1
Відповідь:
6
m 1
1.
n 6
20.
21.
8. У мішку 50 деталей, з них 5 забарвлених. Навмання виймають однудеталь. Знайти ймовірність того, що ця деталь пофарбована.
Розв’язання:
Скільки всього можливо результатів досвіду? Скільки можна вийняти
деталей і забарвлених, і нефарбованих?
n=50
З них можна вийняти тільки 5 забарвлених деталей, тому
m=5
Таким чином, отримуємо:
m 5
1
P( A)
1.
n 50 10
Відповідь:
0,1
22.
9. З урни, в якій знаходиться 4 білих, 9 чорних і 7 червоних куль,навмання виймають одну кулю. Яка ймовірність подій: А-поява білої
кулі; В - поява чорного кулі; С-поява червоної кулі; D-поява зеленої кулі?
Розв’язання:
Кількість вісх можливих результатів n=4+9+7=20.
Дослідів, в результаті яких може бути вийнята біла куля m=4.
P ( А)
m
4
1
1.
n
20
5
Дослідів, в результаті яких може бути вийнята чорна куля m=9.
P( В)
m
9
1.
n
20
Дослідів, в результаті яких може бути вийнята червоний куля m=7.
m
7
1.
n
20
Дослідів, в результаті яких може бути вийнята зелену кулю m=0 і P(D)=0.
P (С )
1 9 7
Відповідь: 5 , 20 , 20 , 0.
23.
10. Дві грані кубика пофарбовані в синій колір, три - взелений, і одна - в червоний. Кубик підкидають один раз.
Яка ймовірність того, що верхня грань кубика виявиться
зеленої?
Розв’язання:
Скільки всього можливо результатів досвіду?
У кубика всього 6 граней, тому можливо 6 результатів досвіду :
n=6
Як знайти m? Для цього потрібно порахувати грані кубика,
які нас цікавить кольору, т.е. m=3
Тоді ймовірність того, що верхня грань кубика виявиться
зеленої буде дорівнює::
m 3 1
P ( А) 1.
n 6 2
Відповідь: 0,5
24.
11. Цифри 1,2,3, ..., 9, виписані на окремі картки, складаютьу ящик і ретельно перемішують. Навмання виймають одну
картку. Знайти ймовірність того, що число, написане на цій
картці: а) парне, б) непарна, в) однозначне; г) двозначним.
25.
Розв’язання:Загальна кількість дослідів - це кількість карток, які будуть
зроблені за умовою задачі : n=9
а) Парні числа від 1 до 9 – 2, 4, 6, 8 m=4
Тоді,
P ( А)
m
4
1.
n
9
б) Непарні числа − 1, 3, 5, 7, 9, m=5 Тоді,
P( В)
m
5
1.
n
9
в) Всі числа від 1 до 9 однозначні, т.к. складаються з одного
m
9
P
(
С
)
1.
знака m=9,
тогда,
n
9
г) Відповідно, двозначних чисел серед них немає і m=0 і
P( D)
m
0
0 1.
n
9
4 5
Відповідь: 9 , 9 , 1, 0 .
26. Висновок
Дослідницька робота була цікава і різноманітна. Під час створеннянауково – дослідницької
роботи була досліджена тема «Теорія
ймовірності». Було опрацьовано навчальну літературу. Розглянуто
історію теорії ймовірності, прості та складені випадкові події та
операції над ними, запропоновано класичне означення ймовірності,
знайдено деякі елементи комбінаторики в теорії ймовірностей,
розв’язано задачі з даної теми. Оскільки робота має прикладний
характер, то освоєння даної роботи має практичне значення, адже
отримані знання можуть бути використані в техніці, економіці, у
теоріях надійності та масового обслуговування, у плануванні та
організації виробництва, у страховій та податковій справах, у
соціології, у демографії та охороні здоров’я.























 mathematics
mathematics








