Історична довідка. Випадкові події та операції над ними. Означення ймовірності. Елементи комбінаторики. Лекція 1

1. Лекція 1

Історична довідка. Випадкові події та операції над ними.
Означення ймовірності. Елементи комбінаторики.

2. План лекції:

Організація навчання
Історична довідка
Випадкові події
Операції над подіями
Означення ймовірності
Основні комбінаторні схеми

3. Цікаві факти історії:

Жорж Луи Леклерк Бюффон
(1707, Монбар -1788, Париж )- французький
природознавець, почесний член Петербурзької та
Паризької академій наук, перший хто почав
розв’зувати задачі на геометричну ймовірність.
Всього - 4040 підкидань
Герб – 2048 разів

4. Цікаві факти історії:

Карл Пірсон (1857, Лондон – 1936, Лондон) –
англійський математик, працював професором
Лондонського університету, займався
математичною статистикою.
Всього - 24000 підкидань
Герб – 12012 разів
1970 рік, американські вчені провели
дослід:
Всього - 10000 підкидань
Герб – 4979 разів

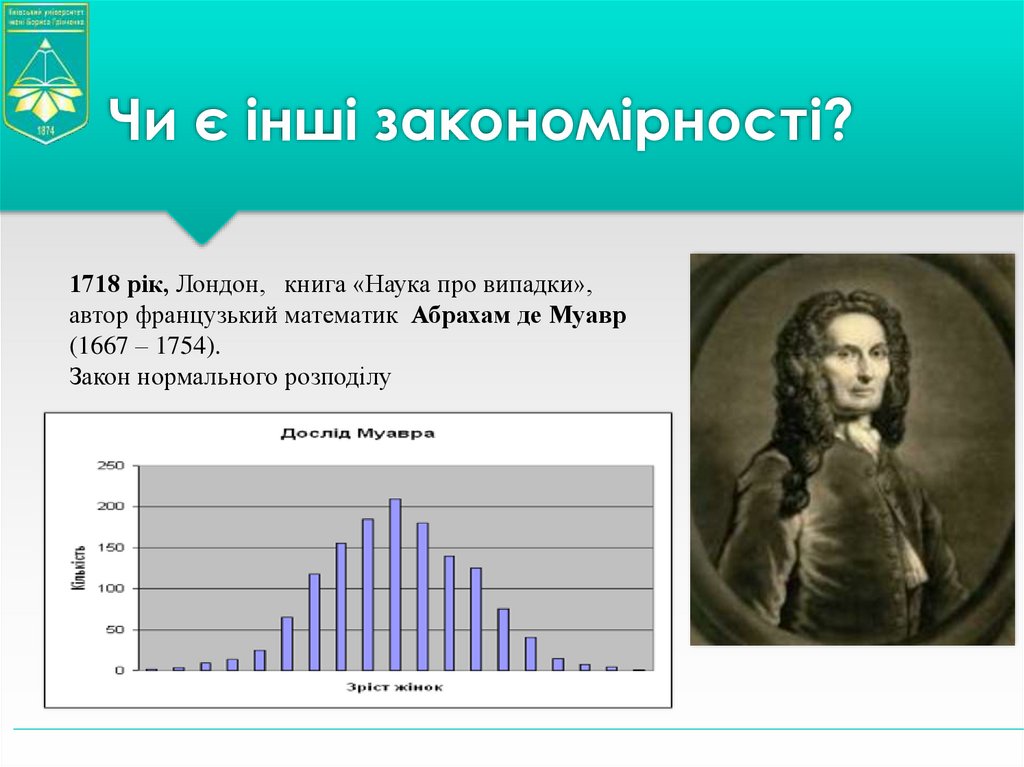
5. Чи є інші закономірності?

1718 рік, Лондон, книга «Наука про випадки»,
автор французький математик Абрахам де Муавр
(1667 – 1754).
Закон нормального розподілу

6. Продовжуємо екскурс

Пьєр Лаплас (1749 – 1827) – французький астроном,
математик, фізик, автор книги «Аналітична теорія
ймовірностей»
« Прекрасно те, що наука, яка почалась із розгляду
азартних ігор, обіцяє стати найбільш важливим
об’єктом людського пізнання. Насправді,
найважливіші життєві питання є по суті лише
задачами теорії ймовірностей»

7. Самостійна робота №1

1.
Блез Паскаль
6.
Сімео́н-Дені́
Пуассо́н
11.
Леонард Ейлер
16.
Віктор
Буняковський
2.
П'єр Ферма
7.
Карл Пірсон
3.
Християн
Гюйгенс
8.
Абрахам де
Муавр
12.
Олександр
Ляпунов
17.
Михайло
Остроградський
4.
Якоб Бернуллі
9.
Жорж-Луї
Леклерк де
Бюффон
13.
Рональд Фішер
14.
Йога́нн Карл
Фрі́дріх Га́усс
18.
Андрій Марков
19.
Пафну́тій
Че́бишов
5.
П'єр-Сімо́н
Лапла́с
10.
Томас Баєс
15.
Жозеф Бертран
20.
Борис Гнєденко
25.
21.
Йо́сип Гі́хман
22.
Анато́лій
Скорохо́д
23.
Михайло
Ядренко
24.
Андрій
Колмогоров
Володимир
Королюк

8. Випадкові події

Експериментом (або випадковим експериментом) називають певний
комплекс умов, що забезпечують спостереження за певним реальним
випадковим явищем (певною реальною випадковою подією).
Кожне окреме проведення експерименту (тобто забезпечення згаданих
умов) називають випробуванням, а відповідний результат випробування
називають його наслідком або елементарним наслідком або елементарною
подією..
Сукупність усіх елементарних подій, пов’язаних з даним експериментом
називають множиною (або простором) елементарних подій.
Приклад. Визначимо експеримент умовами: підкинути монету і
зафіксувати грань, якою монета впаде догори.

9. Випадкові події. Дві події…

Кожну реальну випадкову подію, пов’язану з даним експериментом,
ототожнюють з її математичною моделлю – певною сукупністю результатів
цього експерименту. Такі моделі називають подіями (або випадковими
подіями) і позначають великими латинськими літерами
вірогідна (або достовірна) подія, яка відбувається в результаті кожного
випробування, пов’язаного з даним експериментом
неможлива подія, яка не відбувається в результаті випробування,
пов’язаного з даним експериментом

10. Деякі відомості

Якщо подія А відбувається завжди, коли відбувається подія В, то кажуть,
що подія А спричинюється подією В або подія В спричинює А
Події А і В називають однаковими або рівними або еквівалентними і
пишуть А=В, якщо кожна з них спричинює іншу з них.
Приклад. Підкидається гральний кубик.
Описати простір елементарних подій. Розглянемо події – «випадання
парної кількості очок», «випадання не менше семи очок», «випадання не
більше семи очок», «випадання одного з трьох чисел, добуток яких
дорівнює 48».

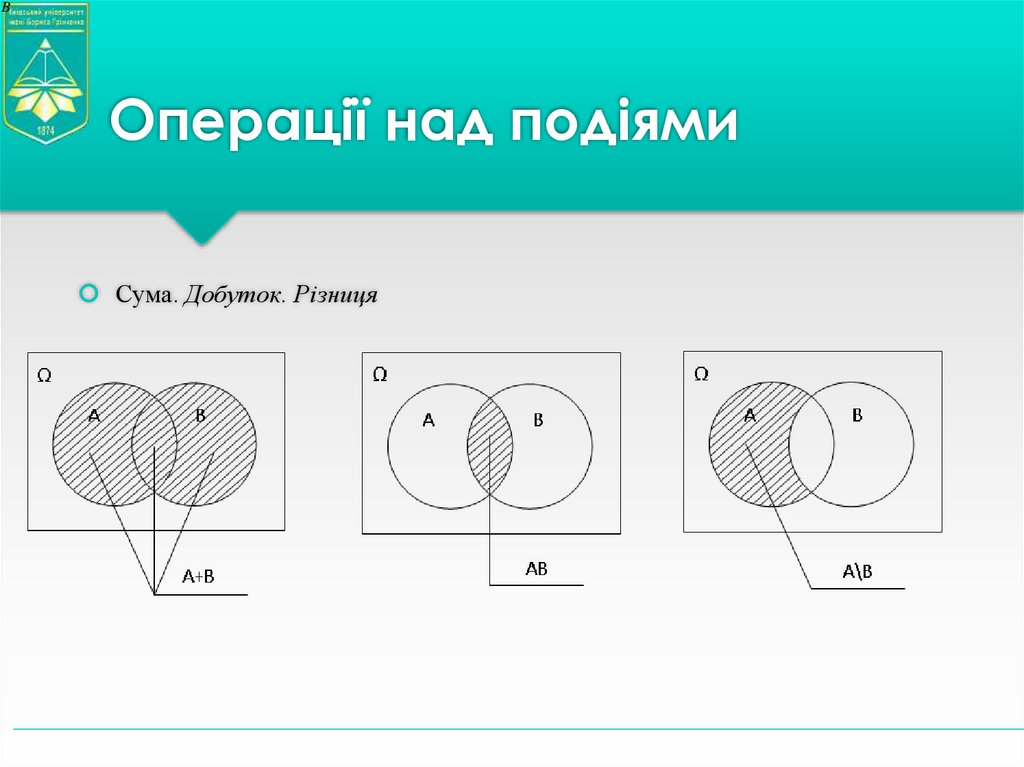
11. Операції над подіями

B
Операції над подіями
Сума. Добуток. Різниця

12. Приклад

Два стрільці роблять постріл у мішень по одному разу.
Подія
А=«у мішень влучив перший стрілець»,
В=«у мішень влучив другий стрілець».
Виразити через А і В такі події:
“два влучення в мішень”,
“жодного влучення в мішень”,
“хоча б одне влучення в мішень”,
“лише одне влучення в мішень”.

13. Статистична ймовірність та її властивості

Pn* ( A)
m
n
Статистична ймовірність та
її властивості
Відносна частота
Відносна частота – це середня можливість появи події А у кожному з n
проведених випробувань.
Якщо виявляється, що для будь-якої події А відносна частота
досить добре характеризує середню можливість появи кожної події А з
подій S у інших серіях випробувань, то тоді
називають статистичними ймовірностями подій
з простору подій S.
простору

14. МІРА

https://www.youtube.com/watch?v=QS6ALAdoq9Y (5.30)
Ці властивості нагадують відомі властивості довжини, площі, об’єму, маси,
які мають спільну назву: міра.
Отже, статистичне ймовірність – це міра можливості появи події у
кожному випробуванні.
Приклад 1. При перевірці готової продукції було виявлено 5 бракованих
одиниць товару з 200 перевірених. Знайти відносну частоту бракованих
одиниць товару.
Приклад 2. При стрільбі по мішені було виявлено, що відносна частота
влучень дорівнює 0,85. Проведено 100 пострілів. Скільки пострілів були
влучними?
Мірою множини на прямій, площині, у просторі є відповідно довжина,
площа та об’єм відповідної геометричної фігури.

15. Означення ймовірності.

Ймовірнісний простір
Сукупність простору
елементарних подій, простору S подій та ймовірностей
P(A),
, називають ймовірнісною моделлю або ймовірнісним простором даного
експерименту
Рівноможливі наслідки
Класичне означення
Приклад. В урні міститься 5 білих, 3 чорних та 4 червоних кульок. Навмання
виймають одну. Знайти ймовірність того, що навмання вийнята кулька є червоною.
Приклад. Знайти ймовірність того, що вибране випадковим чином двозначне
число ділиться на 3.

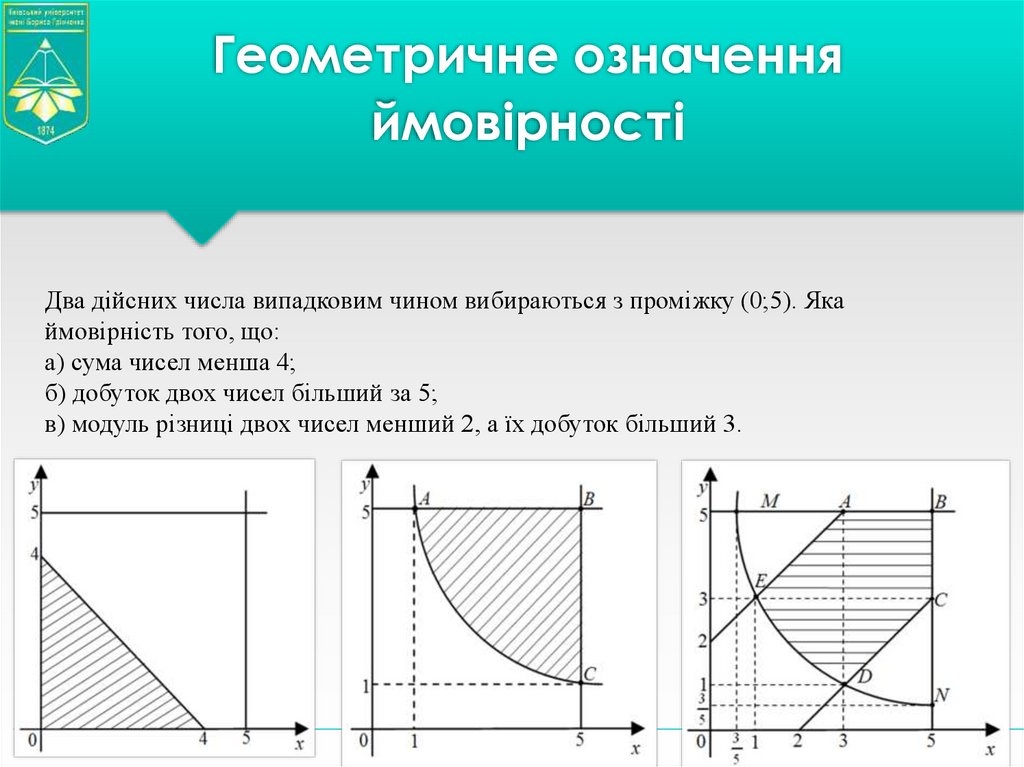
16. Геометричне означення ймовірності

Два дійсних числа випадковим чином вибираються з проміжку (0;5). Яка
ймовірність того, що:
а) сума чисел менша 4;
б) добуток двох чисел більший за 5;
в) модуль різниці двох чисел менший 2, а їх добуток більший 3.

17. Елементи комбінаторики.

Розміщення
Перестановки
Сполучення
Розміщення / Перестановки / Сполучення з ПОВТОРЕННЯМИ

18. Основні формули (схеми без повторень)

19. Приклади

За навчальним планом студенти протягом семестру вивчають 10 дисциплін.
На кожен день плануються 4 пари з різних дисциплін. Скількома
способами можна скласти розклад занять на один день.
Скільки п’ятизначних чисел можна утворити за допомогою цифр 1, 2, 3, 4,
5, якщо кожна з них у числі зустрічається лише один раз?
У групі налічується 15 студентів. Скількома способами можна обрати:
а) студентську раду в кількості трьох студентів;
б) голову, заступника та секретаря студентської ради?
В урні міститься 8 чорних і 5 білих кульок. Навмання виймаються 4
кульки. Яка ймовірність того, що витягнули:
а) 4 чорних кульки;
б) 2 чорних і 2 білих кульки.