Стереометрия. Геометрия

1.

2.

3.

4.

Существует
принадлежит
Пересечение/
пересекаются
Не принадлежит
||
,
a, b
Перпендикулярность/
перпендикулярны
Параллельность/
параллельны
Так обозначаются
плоскости
Так обозначаются прямые

5.

Аксиомы стереометрии
Аксиома 1.
Какова бы ни была плоскость, существуют
точки, принадлежащие этой плоскости, и
не принадлежащие ей.

6.

Аксиома 2.
Если две различные плоскости имеют
общую точку, то они пересекаются по
прямой.

7.

Аксиома 3.
Через две пересекающиеся прямые можно
провести плоскость и притом только одну.

8.

Следствие 1.
Через прямую и не лежащую на ней точку
проходит плоскость и притом только одна.

9.

Следствие 2.
Если две точки прямой лежат в плоскости,
то вся прямая лежит в этой плоскости.

10.

Следствие 3.
Через три точки, не лежащие на одной
прямой, проходит плоскость и притом
только одна.

11.

12.

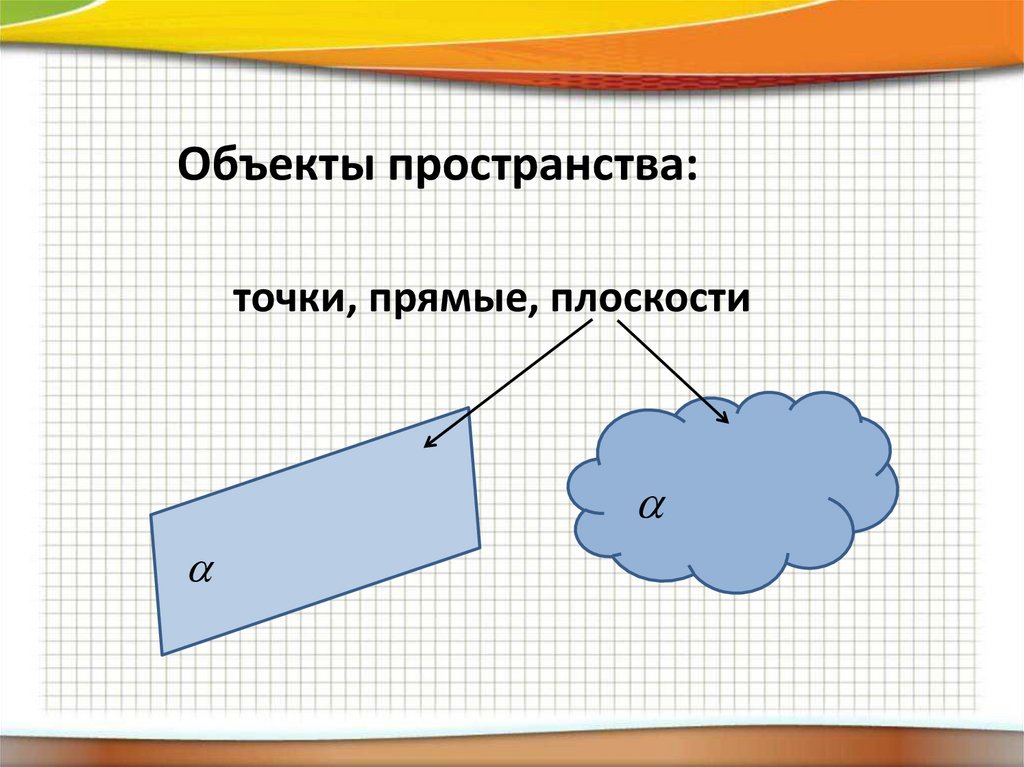
Объекты пространства:
точки, прямые, плоскости

13.

14.

Две прямые называются параллельными,
если они лежат в одной плоскости и не
пересекаются.
Две прямые называются
скрещивающимися, если они лежат в
разных плоскостях и не пересекаются.

15.

Дано: A a
Доказать:
a1 проходящая через А, || a и
притом единственная
А
Доказательство:
а
Проведем через a и A плоскость α.
В плоскости α проведем прямую a1 , || a.
Докажем, что a1 - единственная.
Метод от противного.
Пусть существует a2||a.
Проведем через a и a2 плоскость α2.
Плоскость α2 проходит через a и A .
По следствию 1 плоскость α2 совпадает с α.
Значит, прямая единственная, что и т.д.

16.

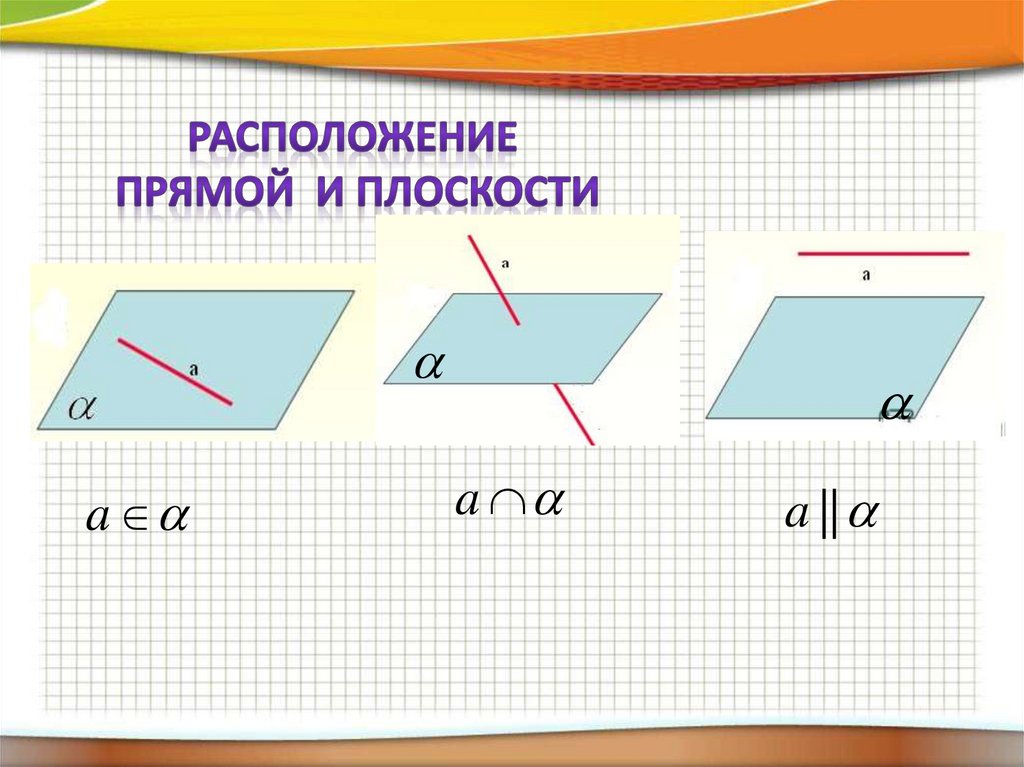
Без докащательства

17.

Прямая и плоскость называются
параллельными, если они не
пересекаются.

18.

a
a
a ||

19.

Дано:
a
Доказать:
a || a1
a ||
Доказательство:
a1
Проведем через a и a1 плоскость α2 .
Плоскости α2 и α пересекаются по прямой a1 .
Метод от противного.
Пусть a пересекает α. Тогда бы a пересекала a1 .
Это противоречит условию a || a1
Значит предположение не верно, то есть, a ||
что и т.д.

20.

Две плоскости называются
параллельными, если они не
пересекаются.

21.

Дано:
Доказать:
b1 b2
b1 b2 ||
||
Доказательство:
b1 b2
Метод от противного.
Пусть плоскости пересекает по прямой с.
Т.к. b и b || значит b1 и b2 не
1
2
пересекаются с прямой с.
Но b1 b2 . Возникло противоречие.
Предположение неверно, плоскости параллельны,
что и т.д.

22.

Без доказательства

23.

1. Если две параллельные плоскости
пересечены третьей, то прямые
пересечения параллельны.

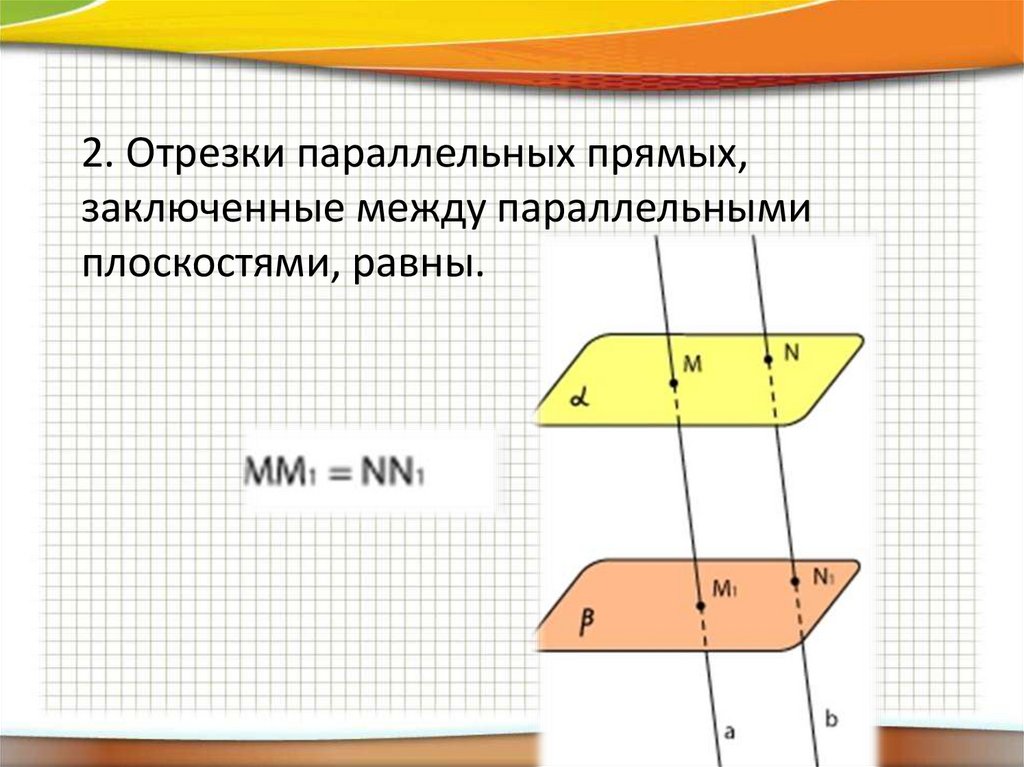
24.

2. Отрезки параллельных прямых,
заключенные между параллельными
плоскостями, равны.