Критерий линейной корреляции Пирсона

1.

Критерий линейной
корреляции Пирсона

2.

Назначение критерия
• Определения силы и направления
корреляционной связи между двумя признаками,
измеренными в интервальной шкале и шкале
отношений.

3.

Виды корреляционных связей
• Положительная (прямая): высоким значениям одного
показателя соответствуют высокие значения другого
показателя, низким – низкие, средним – средние.
• Отрицательная (обратная): высоким значениям одного
показателя соответствуют низкие значения другого
показателя, низким – высокие, средним – средние.
• Не значимая, если нет соответствия между уровнями
признаков.

4.

Ограничение
• Объем выборки должен быть n 2
• Распределение по признакам должны быть
нормальным

5.

Значение критерия вычисляется по
формуле
• Где Xi= xi- Xср; Yi= yi- Yср

6.

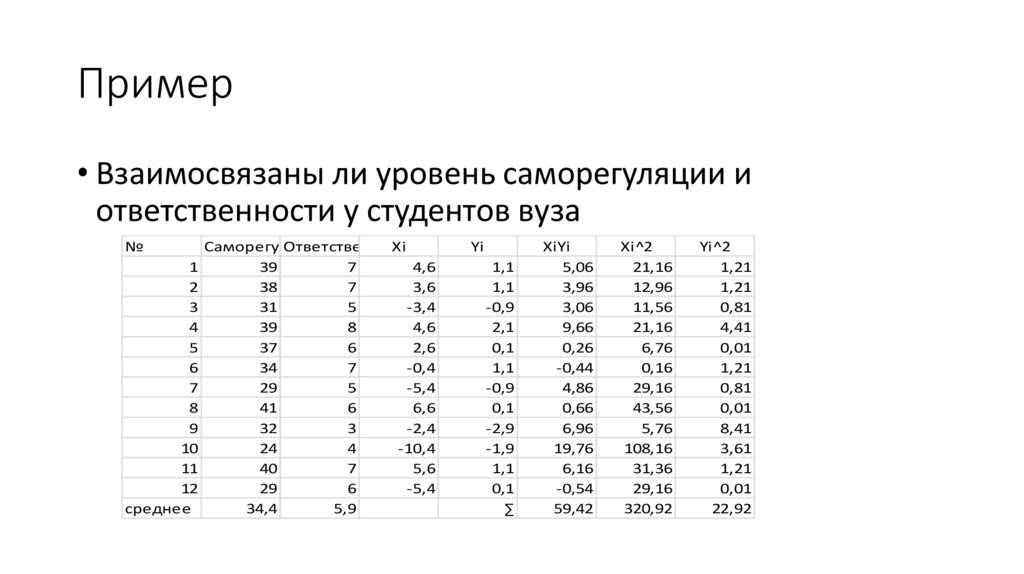
Пример
• Взаимосвязаны ли уровень саморегуляции и
ответственности у студентов вуза
№
1
2
3
4
5
6
7
8
9
10
11
12
среднее
Саморегуляция
Ответственность
Xi
39
7
4,6
38
7
3,6
31
5
-3,4
39
8
4,6
37
6
2,6
34
7
-0,4
29
5
-5,4
41
6
6,6
32
3
-2,4
24
4
-10,4
40
7
5,6
29
6
-5,4
34,4
5,9
Yi
1,1
1,1
-0,9
2,1
0,1
1,1
-0,9
0,1
-2,9
-1,9
1,1
0,1
∑
XiYi
5,06
3,96
3,06
9,66
0,26
-0,44
4,86
0,66
6,96
19,76
6,16
-0,54
59,42
Xi^2
21,16
12,96
11,56
21,16
6,76
0,16
29,16
43,56
5,76
108,16
31,36
29,16
320,92
Yi^2
1,21
1,21
0,81
4,41
0,01
1,21
0,81
0,01
8,41
3,61
1,21
0,01
22,92

7.

Расчет по формуле
59,42
•ρ= ----------------- = 0,693
√390,92*22,92

8.

Гипотезы
• Н1 Взаимосвязь у студентов уровня саморегуляции и
ответственности статистически значима
• Н0 Взаимосвязь у студентов уровня саморегуляции и
ответственности статистически не значима

9.

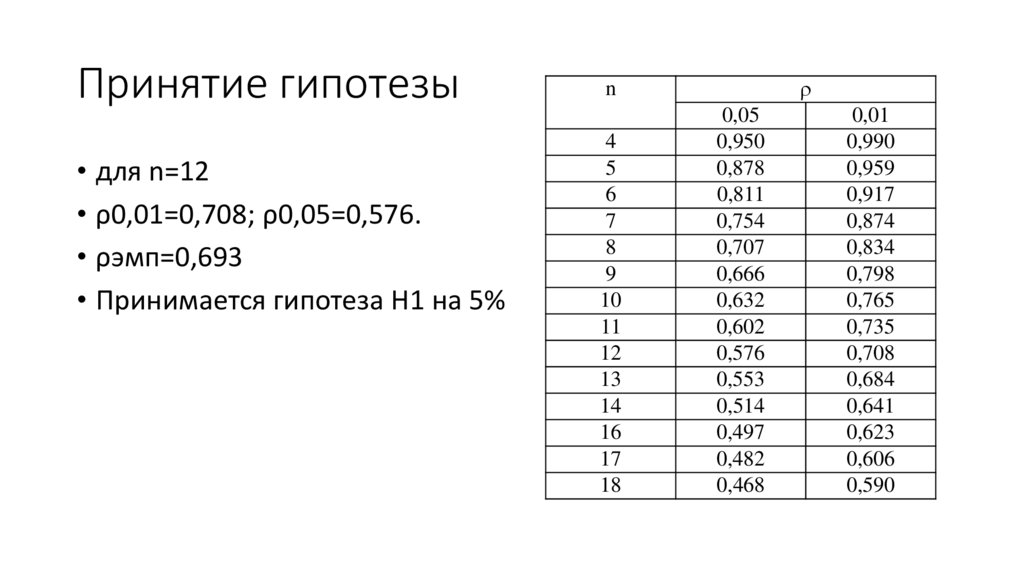
Принятие гипотезы
• для n=12
• ρ0,01=0,708; ρ0,05=0,576.
• ρэмп=0,693
• Принимается гипотеза Н1 на 5%
n
4
5
6
7
8
9
10
11
12
13
14
16
17
18
0,05
0,950
0,878
0,811
0,754
0,707
0,666
0,632
0,602
0,576
0,553
0,514
0,497
0,482
0,468
0,01
0,990
0,959
0,917
0,874
0,834
0,798
0,765
0,735
0,708
0,684
0,641
0,623
0,606
0,590